💍
分散とは

2025/07/30に公開
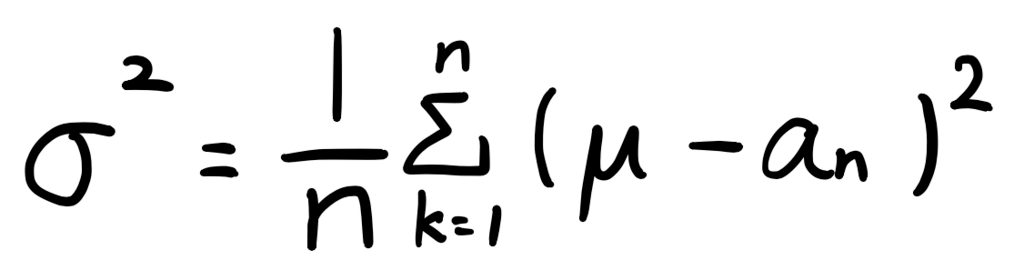
統計学の基本中の基本は平均と、この分散。
分散の理解には平均の理解が前提になる。

 前提知識平均

 分散とは分散とは、イメージとしては「散らばり具合」。名前そのまんま。

具体的には、「平均からの離れ具合の平均」。
たとえばこんなふうにコップに入った水の量を比べる。

赤い線が平均とする。
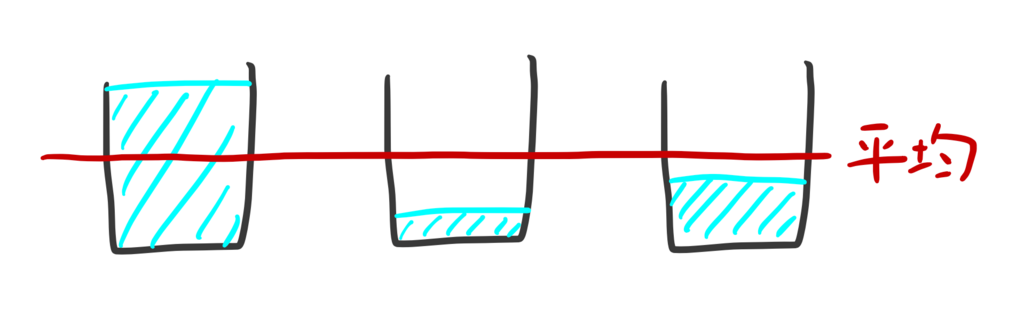
赤い平均の線と水面の距離が、オレンジの矢印。
大雑把に言えば、分散 = このオレンジの矢印の長さの平均※。
※正確にはこれは分散でなく平均偏差（あとで説明する）だが、いったんこんなイメージでOK。

 分散を求める
 偏差さっきのコップの例で、分散を実際に求める。

水の量をそれぞれ10、2、3とする。すると、平均は5になる。
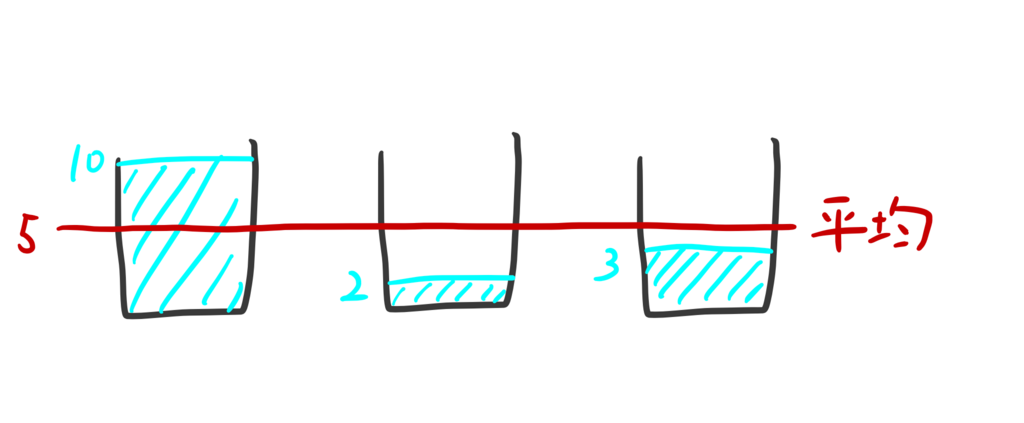
コップごとに、水の量と平均の差（離れ具合）を求める。
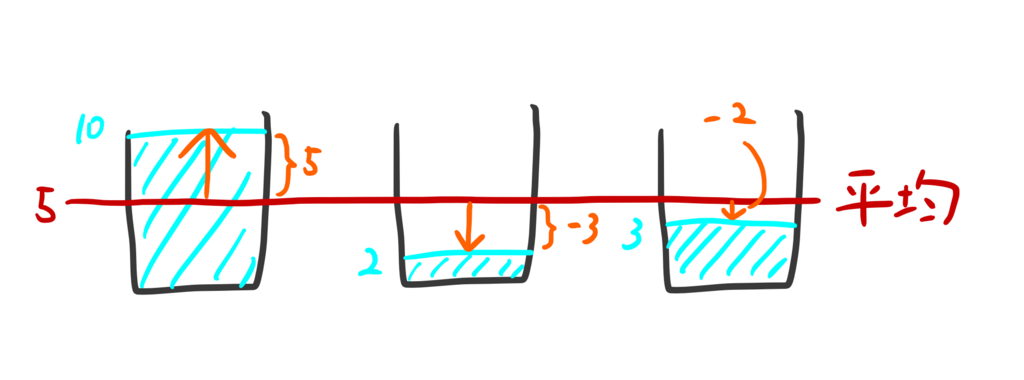
これを 偏差 という。

\text{偏差} = \text{サンプルの値} - \text{平均}

 偏差の平均分散を求めるというのは、気持ちとしてこの偏差の平均を求めたいということ。
じゃあ今回はこうすればよい？

\frac{5+(-3)+(-2)}{3}
これだと、正の値と負の値で打ち消しあってしまって、「平均からの離れ具合」という趣旨からずれてしまう。

上に大きく離れたサンプルがあっても、そのぶん下に大きく離れたサンプルがあれば「散らばっていない」となるのはおかしい。それは「散らばっている」はず。

 ついに分散この問題を解消するのは簡単。マイナスの符号をとってしまえばいい。そのために、すべての偏差を２乗してから平均を求める。

\frac{5^2+(-3)^2+(-2)^2}{3}
これが、分散。今回は

\frac{5^2+(-3)^2+(-2)^2}{3} = \text{およそ} 12.7
一般化するとこう書ける。
サンプル数を n 、 n 番目の偏差を 偏差_n とすると、

\text{分散} = \frac{{偏差_1}^2+{偏差_2}^2+ \cdots +{偏差_n}^2}{n}
マイナスをとりたいだけなら２乗せずとも絶対値でよいのでは？と思われるかもしれないが、それは後ほど。

 分散の表記上で求めたように、分散は 偏差の２乗を平均したもの 。
なので、分散はこう表記する。

\text{分散 :} \quad \sigma^2

 標準偏差分散が \sigma^2 なら、 \sigma つまり \sqrt{\sigma^2} もある。これを 標準偏差 という。

\text{標準偏差 :} \quad \sigma = \sqrt{\sigma^2}
そもそも、「平均からの離れ具合の平均」を求めたいのだった。なので、２乗で大きくふくらんでしまった分を元に戻した標準偏差の方が感覚的に近い。
たとえば、あるサンプルの偏差が 1.2\sigma だったら、そのサンプルは平均的な離れ具合よりおよそ1.2倍離れているとわかる。

 平均偏差しかしながら標準偏差はそのまま「平均からの離れ具合の平均」ではない。計算してもらえばわかるが、２乗を足し合わせておいて最後に \sqrt{} にいれても、マイナスを除去しただけ、ということにはならない。
なので最初から２乗でなく絶対値を足し合わせる方法がある。こうして求めたものを 平均偏差 という。偏差の平均だからそのままの名前。

\text{平均偏差} = \frac{|偏差_1|~+~|偏差_2|~+~ \cdots ~+~|偏差_n|}{n}
これならちょうど「平均からの離れ具合の平均」になる。
しかし平均偏差はあまり使われない。理由は 扱いにくい から。絶対値は扱いにくい。

 散らばり具合の指標として「平均からの離れ具合の平均」として、より正確なのは 平均偏差 。しかしその扱いにくさゆえ、統計学では 分散 と 標準偏差 が「散らばり具合の指標」として用いられる。
これに問題はないのか。
ない。
そもそも、「散らばり具合の指標」がぴったり「平均からの離れ具合の平均」である必要はない。「散らばり具合に追従する数字」ならいいのだ。ただ、「平均からの離れ具合の平均」に 近い ほうが直感的にイメージしやすいというだけだ。
なので、統計学では扱いにくい平均偏差でなく分散と標準偏差を「散らばり具合の指標」として採用している。
...と思う。