CSS大解剖 5日目: 「閲覧環境 3/3」
本稿は、2024年2月頃に書き溜めていたシリーズです。最後まで温存させるのが勿体ないので、未完成ですがそのまま公開します(公開日: 2025/9/21)。そのため、内容の重複や記述方針の不一致があるかもしれませんが、ご理解ください。
CSSの仕様を理解するために、1日ごとにテーマを決めて説明する企画5日目です。今日のテーマは前回に引き続き「閲覧環境」です。
色
「色」は非常に複雑な概念です。ここでは、sRGB色空間がヒトの色の知覚に対してどのように定義されているかの説明を試みます。
「色」は広義にはヒトの目が物体の材質に大して認知しうる様々な詳細を含んでいます。たとえば以下のようなものも「色」と呼ばれることがあります。
- 金色/銀色/玉虫色 ... 光源や視点の移動に対する振る舞いを表現したもの。
- 虹色 ... 模様。
- 透明 ... 他の色との合成比率。
このうち透明度については後述しますが、このような特殊な色については本稿の対象外と考えます。
こういったものを取り除いた「単色」は、目に入力される時点では可視光のスペクトルという形の情報になっています。つまり、どのような波長の光(nm)が、それぞれどれくらいの強さ(W/m^2)で入射しているかという情報です。一般的なヒトは、この情報を以下のような手順で処理します。
- 光学的なフィルタリング。
- 瞳孔による絞りによる明るさ調整。
- 水晶体や中心窩のフィルターによるスペクトルの調整。
- 生体信号への変換。
- 明所では3種類の錐体細胞 (L錐体, M錐体, S錐体) の活性による3自由度の信号。
- 暗所では桿体細胞の活性による1自由度の信号。
- このとき、錐体細胞/桿体細胞は直前に見ていたものに合わせて活性が変わります (順応)。
- 網膜内での信号処理。
- L/M/Sの入力はこの時点でルマ(明るさ成分; 1自由度)とクロマ(色成分; 2自由度)に分離されます。
- また、エッジ検出などの局所的な情報処理が行われ、情報量は1/10以下に圧縮されます。
- 脳内での信号処理。
- 非常に複雑な処理を経て、物体が認識されます。
- この時点で、さらに色の補正が行われます。
ここで重要なのは以下の点です。
- 単色の認知はL/M/Sに由来する3自由度に制約される。[1]
- ヒトの視覚の感度はエネルギーに比例するわけではない。
- 情報処理の様々な段階で、環境にあわせた色補正が行われている。
- 個体や左右の目の違い、利用する視野の違いによっても色の知覚には差異がある。
カラリメトリーの2段階
色の数理モデルは以下の2段階に分けられます。
- 狭義のカラリメトリー: 可視光のスペクトルを色として分類する。
- 広義のカラリメトリー: 可視光がどのような色として認識されるかを、環境を考慮に入れた状態でモデル化する。
環境を考慮した広義のカラリメトリーは本稿のスコープを大きく逸脱するため、ここでは狭義のカラリメトリーを中心に説明します。
LMS色空間
LMS色空間は錐体細胞の応答をそのまま表現した色空間です。これは特定の計算方法を指してはいませんが、L, M, Sに対応する等色関数 (color matching function) と可視光のスペクトルとの内積を取ることで得られます。したがって、この色空間の量は物理量に比例しています。
全ての色は非負のL, M, S値をとりますが、逆は真ではありません。非負のL, M, S値をもつ色でも、実在(可視光のスペクトルに対応)しない場合があります。
輝度とXYZ色空間 (CIE 1931)
CIE 1931はLMS色空間を線形変換したもので、Y成分が輝度に対応します。歴史的にはLMS色空間よりもXYZ色空間のほうが先に作られたようです。このXYZ色空間にもCIE 1931以外にいくつか亜種があるようですが、ここで述べる原則は同様に通用するはずです。
ヒトはL, M, S錐体の入力の混合によって明るさを判定しているため、Y成分はその混合率を反映する形で計算されています。ただし、暗所で使われる桿体細胞は錐体細胞の混合とは異なる反応を示します。錐体細胞の混合によって判定される明るさの反応は550nm付近(黄緑; やや黄色寄り)にピークがありますが、桿体細胞によって判定される明るさの反応は540nm付近(黄緑; やや緑寄り)にピークがあり、ズレがあります。Webコンテンツを暗視状態で見ることはあまりないと思うので、基本的には錐体細胞をもとにした明るさで考えてよいでしょう。
全ての色は非負のX, Y, Z値をとりますが、逆は真ではありません。なお、X成分とZ成分のLMS混合率は、全ての色を非負座標でギリギリ表せるように調整されています。
xyY色空間
XYZ色空間におけるスカラー倍は、輝度の違う同じ色彩を表しているものと考えられます (グラスマンの法則)。そこでこの座標を X + Y + Z = 1 となるように正規化することを考えます。
こうして得られた座標は (x, y, z) (x >= 0, y >= 0, z >= 0, x + y + z = 1) と表されますが、等式制約を消去して (x, y, 1 - x - y) (x >= 0, y >= 0, x + y <= 1) としたほうが便利です。この (x, y) が色彩成分を表すことになります。
色彩成分である (x, y) に輝度情報である Y を足したものをxyY色空間といいます。
ここまでの話をまとめると以下の図になります。 (伝わるかはわかりませんが……)
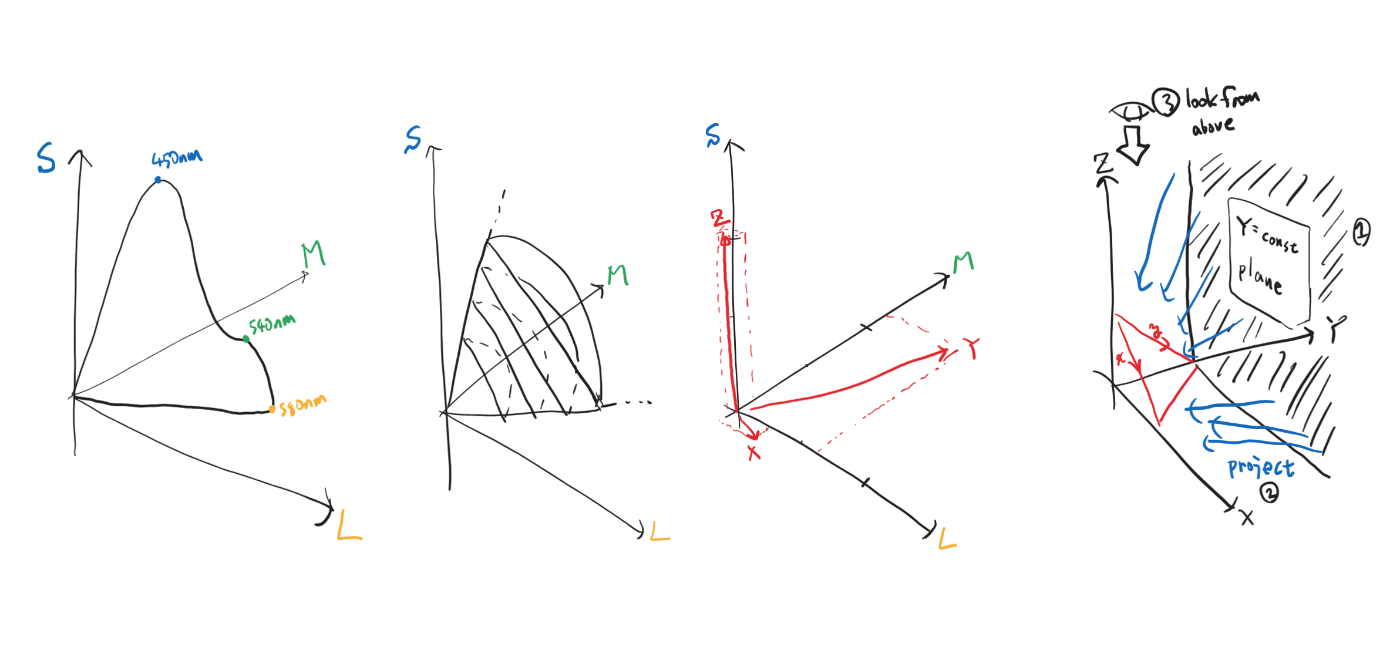
- 1枚目: 単色光のLMS色空間上の配置
- 2枚目: 単色光のLMS色空間上の凸包。かまぼこ形の底面を持つ無限錐の形をしている。
- 3枚目: LMS色空間からXYZ色空間への変換。直交変換ではないことに注意。XZが張る平面が等Y面になっている。2枚目で示した無限錐は、このXYZの非負線形結合が張る空間に収まる。
- 4枚目: XYZ色空間の等Y断面をとり、それを等X+Y+Z面に射影する。この断面上の座標がxy。これを上から見たものが、よく見る色彩の図。
白点
「黒」「灰色」「白」などの色はニュートラルな色として知覚されます。これは輝度の違いを除くとある色彩の範囲を指し示しています。このような色を白点といいます。
「白」はヒトの知覚としては確かに存在する概念ですが、ここまでの(XYZやxyの)定義からアプリオリに定まるものではありません。かわりに、用途にあわせてイルミナント(光源[2])を選択し、そのイルミナントの色を白と定めることになります。
D65はそのようなイルミナントのひとつで、平均的な昼光に相当するものです。D65に対応する白点は、CIE 1931のxy平面上では (0.3127, 0.3290) にあります。
ガンマ補正とダイナミックレンジ
ここまでは線形変換や射影変換だけで説明できる範囲内の内容でしたが、ヒトの知覚には非線形成分が含まれます。また、映像や画像を取り扱う機器の振る舞いも入力に対して非線形であることが一般的ですし、入力を量子化するにあたっての最適な階調も同様に非線形です。
これらの知覚や機器の振る舞いはおおむねべき乗則に従うことが多く、数学的には同じような変換で処理できます。これをガンマ補正といいます。
また、入力を8bitや16bitなどの小さい整数値に量子化する際は、入力のオーバーフローと量子化による情報ロスがトレードオフの関係にあり、この限界ダイナミックレンジといいます。これらの両立をはかる画像処理はHDRIと呼ばれます。たとえば、整数のかわりに32bit浮動小数点数を使って三刺激値を表現するという方法が考えられます。
sRGB
sRGBはコンピューター向けに広く使われている色空間であり、赤・緑・青の3つの原色の組み合わせで色を表現するRGB色空間の一種です。
XYZ色空間が実際の色を全て含むように広めに定義されているのに対し、RGB色空間は空間内の全ての色が実在するように狭めに定義されています。RGB色空間で表現できないものとして以下が挙げられます。
- 彩度の高い色、特に緑系の色。これはより彩度の低い色で代替されます。
- 輝度の高い色。これはより輝度の低い色で代替されます。
- また、これはsRGB自体の問題ではありませんが、sRGBの応用は一般的に量子化をともなうため、量子化による誤差が発生します。
XYZ (CIE 1931) からsRGBを得るには以下の手順を踏みます。
- 輝度の正規化
- 線形変換とクリッピング
- 非線形変換 (ガンマ変換)
まずはじめに、sRGBは最大輝度に限りがある有界な色空間であるため、最大輝度を決めておく必要があります。最大輝度がY=1となるように、XYZの色ベクトルをスカラー定数倍しておきます。
最大輝度がY=1となるように正規化できたら、線形なRGB刺激値に線形変換します。この線形変換は以下のように定められています。
- 赤の原色の単位ベクトルはxy平面上で (0.6400, 0.3300) にある。
- 緑の原色の単位ベクトルはxy平面上で (0.3000, 0.6000) にある。
- 青の原色の単位ベクトルはxy平面上で (0.1500, 0.0600) にある。
- 上記の3つのベクトルの和 (白色) はxy平面上で (0.3127, 0.3290) にある。
- 上記の3つのベクトルの和 (白色) のY値は1である。
上の制約がちょうど9自由度ある行列を一意に定めます。具体的な行列は以下の通りです。
このとき、R, G, Bの値は
- 負値の解消 (彩度情報の欠落)
- R, G, B値のうち最大2つが負値になっている可能性があります。残る値のうち1つ以上は正値です。
- その場合、まず
Y = 0.2126R + 0.7152G + 0.0722B - 記録していた輝度をもとに、
Y = 0.2126R + 0.7152G + 0.0722B (R, G, B)
- 大きい値の解消 (輝度情報の欠落)
- 負値の解消後
k = \max \{ R, G, B \} k > 1 (R, G, B) 1/k
- 負値の解消後
これにより線形なRGB値が得られますが、sRGBの最終的な値はこれに非線形変換 (ガンマ変換) を加えることで得られます。これはR, G, Bのそれぞれの値 (以下
-
0 \leq x_{\mathrm{linear}} \leq 0.0031308 x_{\mathrm{nonlinear}} = 12.92x_{\mathrm{linear}} -
0.0031308 < x_{\mathrm{linear}} x_{\mathrm{nonlinear}} = 1.055{x_{\mathrm{linear}}}^{1.0/2.4}-0.055
これはおおむね指数1/2.2のべき乗則に従っていますが、値が小さいときの挙動を指定するために場合分けが行われています。
sRGBの特性
sRGBの注意すべき特性として以下があります。
- 全ての色彩を表現できません。これ自体は情報処理用のほとんどの色空間に共通する性質ですが、特にsRGBはブラウン管の挙動に合わせて設定されているため特異的に色域が狭いです。特に緑～青緑の彩度の制限に注意が必要です。
- 輝度が制限されています。明るいものを表現するときは基準となる輝度を上げる必要がありますが、その際量子化精度が下がります。両立するにはHDRIが必要になるでしょう。
- 物理量に対して線形ではありません。これは限られた量子化精度を有効に使うことができる他、過去にブラウン管ベースの情報処理システムへの適合が容易だったという利点がありますが、計算時は注意が必要です。
「RGB色空間」は同様の三原色を持つ色空間の総称であり、sRGB以外にもたくさんの色空間があります。
CMYK
CMYKは印刷でよく用いられる色モデルの総称で、シアン・マゼンタ・黄色の3つの原色と黒インクの減法混色によって色を表現します。黒は単純化したモデルでは三原色の組み合わせで表現できますが、実用上の理由から導入されています。
印刷ではインクを重ねることで紙面が光を吸収しやすくなります。これにより反射光が減少し所望の色が表現されます。
CMYKをXYZに対応づけるには特定のイルミナントを想定する必要があります。印刷物は自己発光しないため、表現できる色はイルミナントの色からの減算で作られる範囲に限られます。加えて、RGBと同様、原色を3種類に限定していることによっても表現の範囲が限定されます。
透明度とアルファブレンディング
透明度は物体の質感を決める要素のひとつで、物体の奥からくる光をそのまま通過させる割合をあらわしています。したがって、ここまでの議論における「色」の定義には含まれていません。
しかし、このような視覚効果をコンピューター上で実現したい機会が非常に多いことから、多くの画像処理システムではR, G, Bに準ずる4つ目のチャンネルとしてアルファチャンネルを表現できるようになっています。このアルファチャンネルを使って擬似的に透明度を表現する仕組みがアルファブレンディングです。
アルファ値は0以上1以下の実数です (8bitであれば255倍して表現されます)。0が透明、1が不透明に対応します。アルファブレンディングでは通常、2つのRGBAカラーを混合する操作を定義し、それを各ピクセルに適用することで2つの画像を混合します。この混合操作には様々な種類がありますが、最も基本的なブレンディングは
\alpha_3 = 1 R_3 = (1 - \alpha_2)R_1 + \alpha_2R_2 G_3 = (1 - \alpha_2)G_1 + \alpha_2G_2 B_3 = (1 - \alpha_2)B_1 + \alpha_2B_2
さらにこれは、ブレンド演算に結合法則を課すことで、
\alpha_3 = \alpha_1 + \alpha_2 - \alpha_1\alpha_2 \alpha_3R_3 = (1 - \alpha_2)\alpha_1R_1 + \alpha_2R_2 \alpha_3G_3 = (1 - \alpha_2)\alpha_1G_1 + \alpha_2G_2 \alpha_3B_3 = (1 - \alpha_2)\alpha_1B_1 + \alpha_2B_2
さてこのブレンディングはRGB空間の線形構造に依存しているため、ガンマ補正後の値でそのまま演算した場合と、ガンマ補正前の数値に戻してから演算して再度ガンマ補正した場合で結果が異なる点に注意が必要です。より光学的に自然なブレンディングを求めるのであれば、ガンマ補正を外してから演算するのがいいかもしれません。
デバイスの実装
ここまでは色の物理的な定義の話ですが、色を表示するデバイスにはそれぞれに固有の制限や工夫があります。
- 全ての色彩を表現できるデバイスはほぼ存在しません。フルカラーと呼ばれているようなデバイスでも、一般的に緑方向の彩度に制限があります。
- ブラウン管や液晶ディスプレイは三原色をそれぞれ出力して混色しており、拡大するとサブピクセルがわかる場合があります。サブピクセルを考慮して色を設定することでより滑らかな表示を目指すような工夫を行っているコンテンツもあるようですが、解像度の高いディスプレイが流通するようになった現代ではあまり見られないかもしれません。
- 同様に、印刷機はインクをドットの集まりとして出力することが多く、拡大すると原色が見えることがあります。
- デバイスによっては各ピクセルに指定できる色に限りがあり離散的にしか色を指定できない場合もあります。このような場合に、ソフトウェア側で原色の配置を調整することで擬似的に混色を実現する場合もあるようです。
- もちろん、グレースケールや白黒による表示しかできないデバイスもあります。
CSSと色
- CSSには画面の色表示能力を識別するメディアクエリがあります。
- カラープロファイル指定のある画像はその指定の通りに、指定のない画像はsRGBと仮定して表示するよう規定されています。ただし、動画に関しては別のルールが適用されます。
-
#RRGGBBなどの16進記法、rgb(),rgba(),blueなどの名前のついた色,hsl(),hsla(),hwb()はsRGBに解決されます。それ以外のcolor()などの記法を使うことで、sRGBの範囲外の色を指定することができます。 - 色の混合計算等を行うときの色空間の選び方には自由度があり、その選択はある程度実装者に委ねられています。
音声
CSSは主に視覚的な表示を指定するために使われますが、音声インターフェースの制御に関する指定もあります。
このうち最も重要なのはdisplay: noneで、これは視覚的な表現だけではなく音声表現にも影響を与えるよう規定されています。それ以外のほとんどの視覚的なプロパティーは音声表現には影響を与えません。
音声表現を直接制御するためのプロパティーはCSS Speech Moduleに規定されています。
また、Working DraftであるSelectors Level 4のTime-dimensional Pseudo-classesも音声インターフェースでの利用が想定されています。たとえば音声と視覚の両方の表現を利用したいユーザーに対して、その表示位置の同期を取りやすくするために使うことができると考えられます。
Discussion