Stim 使ってみる (量子) #3 復号グラフ
復号グラフについて
前回の記事 (#2) では復号グラフの一部の説明を省いていた。復号グラフに現れる L1という記号についてである。これはパウリフレームと呼ばれし、どのデータ量子ビットのビット値が反転されているのかを示している。このL<番号>について詳しくみてみる。
5量子ビット符号距離3の反復符号
今回も3量子ビットを用いたエラー検出符号の回路を考える。初期化エラーの導入から最初のシンドローム測定の部分までを実行した例を下記に示す。初期化のエラーが分極解消エラーだと気持ちが悪いため、今回は X_ERROR を用いた (In[2])。データ量子ビットのエラー検出に用いるCNOTは理想的とする。アンシラ量子ビットの測定の時のエラーと、測定をせず待機しているデータ量子ビットの分極解消エラーを追加した。
In [1]: import stim
...: import numpy
...: d = 3
...: p_init = 0.10
...: p_meas = 0.03
...: circuit = stim.Circuit()
In [2]: circuit.append( 'R', [ i for i in range( 2 * d - 1 ) ])
...: circuit.append( 'X_ERROR', [ i for i in range( 2 * d - 1 ) ], p_init )
...: circuit.append( 'TICK' )
In [3]: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2 ) ])
...: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2, 0, -1 ) ])
...: circuit.append( 'TICK' )
...: circuit.append( 'DEPOLARIZE1', [ i for i in range( 2 * d - 1 ) ], p_meas )
...: circuit.append( 'MR', [ 2 * i + 1 for i in range( d - 1 )] )
In [4]: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( d - 1 ) + i ) ] )
...: circuit.append( 'TICK' )
符号距離 d を変えても回路が動くように多くのインデックスを用いた。ここで符号距離 d とは、論理ビットの状態 ( d = 3 だと000 や 111 )の間のハミング距離であり、ハミング距離とは状態を入れ替えるために必要な反転の数としておく。論理ビットを Q0 Q2 = 00 と 11 を用いるとすると、状態を入れ替えるためには2回ビット反転が必要なため符号距離は d = 2 である。ここでインデックスを整理しておく。
| インデックス | 範囲 | d =3 の例 | |
|---|---|---|---|
| i | range( 2 * d - 1 ) | 0 1 2 3 4 | 全量子ビットのインデックス列挙 |
| i | range( 2 * d - 2 ) | 0 1 2 3 | CNOT用 0->1, 2->3 |
| i | range( 2 * d - 2, 0, -1 ) | 4 3 2 1 | CNOT用 2->1, 4->3 |
| 2 * i + 1 | range( d - 1 ) | 1 3 | アンシラ量子ビット列挙 |
| 2 * i | range( d ) | 0 2 4 | データ量子ビット列挙 |
| - ( d - 1 ) + i | range( d - 1 ) | -2 -1 | 直近のアンシラ量子ビット測定記録 |
| -( d - 1 ) * 2 + i | range( d - 1 ) | -4 -3 | 1周前のアンシラ量子ビット測定記録 |
| - d + i | range( d ) | -3 -2 -1 | 直前のデータ量子ビット測定記録 |
| -( 2 * d - 1 ) + i | range( d - 1 ) | -5 -4 | 最後のデータ量子ビットを読む直前の |
| = -( d + d - 1 ) + i | アンシラ量子ビット測定記録 |
In [5]: detector_block_text = ''
...: for i in range( d - 1 ):
...: detector_block_text \
...: += 'DETECTOR rec[{0}] rec[{1}]\n'.format( -( d - 1 ) * 2 + i ,
...: -( d - 1 ) + i )
In [6]: detector_block_text
Out[6]: 'DETECTOR rec[-4] rec[-2]\nDETECTOR rec[-3] rec[-1]\n'
In [7]: repeat_block_text = '''
...: CNOT {0}
...: CNOT {1}
...: TICK
...: DEPOLARIZE1({5}) {2}
...: MR {3}
...: {4}
...: TICK
...: '''.format(
...: ' '.join( [ str( i ) for i in range( 2 * d - 2 ) ] ),
...: ' '.join( [ str( i ) for i in range( 2 * d - 2, 0, -1 ) ] ),
...: ' '.join( [ str( i ) for i in range( 2 * d - 1 ) ] ),
...: ' '.join( [ str( 2 * i + 1 ) for i in range( d - 1 )]),
...: detector_block_text,
...: p_meas )
In [8]: print(repeat_block_text)
CNOT 0 1 2 3
CNOT 4 3 2 1
TICK
DEPOLARIZE1(0.03) 0 1 2 3 4
MR 1 3
DETECTOR rec[-4] rec[-2]
DETECTOR rec[-3] rec[-1]
TICK
In [9]: circuit.append_from_stim_program_text( 'REPEAT 32 {{\n {}\n}}'.format( repeat_block_text ))
In [10]: circuit.append( 'MR', [ 2 * i for i in range( d )] )

ここでは最初の検出器の追加(Out[6]、改行コードをはさんで2つ追加されている)と繰り返しループ内のシンドローム抽出操作と検出器の追加を記述している。ブロック内はIn[8]のように平文のStimが記述される。最後にデータ量子ビットの測定を追加した(In[10])。
In [11]: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( 2 * d - 1 ) + i ),
...: stim.target_rec( - ( d ) + i ),
...: stim.target_rec( - ( d ) + i + 1 ) ] )
In [12]: for i in range( d ):
...: circuit.append( 'OBSERVABLE_INCLUDE', [ stim.target_rec( - d + i ) ], i )
終端処理用の検出器の追加とデータ量子ビット測定値を追加する。OBSERVABLE_INCLUDEはどの測定値を追加するのかを指定し stim.target_rec( .. )、次の引数でデータ量子ビットの番号をつける。この番号が復号グラフに現れる L0、L1、L2などの記号に対応する。
In [13]: circuit
Out[13]:
stim.Circuit('''
R 0 1 2 3 4
X_ERROR(0.1) 0 1 2 3 4
TICK
CX 0 1 2 3 4 3 2 1
TICK
DEPOLARIZE1(0.03) 0 1 2 3 4
MR 1 3
DETECTOR rec[-2]
DETECTOR rec[-1]
TICK
REPEAT 1 {
CX 0 1 2 3 4 3 2 1
TICK
DEPOLARIZE1(0.03) 0 1 2 3 4
MR 1 3
DETECTOR rec[-4] rec[-2]
DETECTOR rec[-3] rec[-1]
TICK
}
MR 0 2 4
DETECTOR rec[-5] rec[-3] rec[-2]
DETECTOR rec[-4] rec[-2] rec[-1]
OBSERVABLE_INCLUDE(0) rec[-3]
OBSERVABLE_INCLUDE(1) rec[-2]
OBSERVABLE_INCLUDE(2) rec[-1]
''')
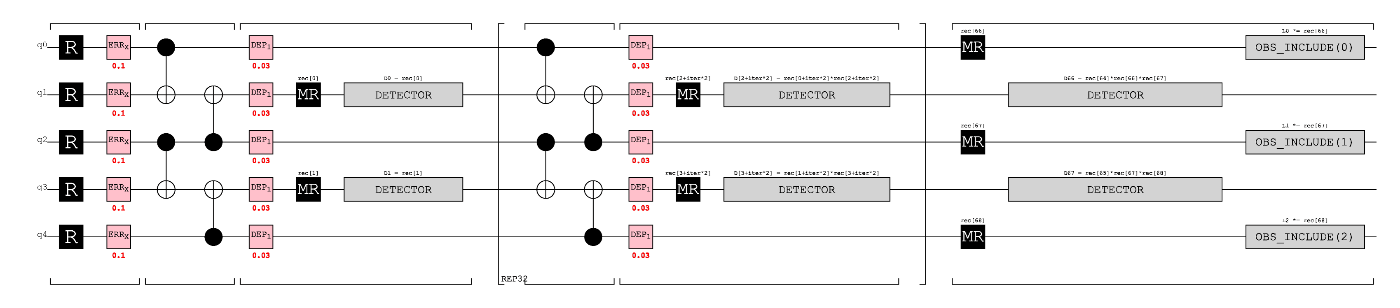
(画像では検出器の位置をいじってある)
復号グラフと観測値
復号グラフを表示する。前回#2説明した通り、errorがグラフの辺とその重みを表しており、D<数字>がノードを示す検出器である。ループ中のshift_detectors により検出器の番号が繰り上がっていくことに注意されたい。ここで L0 と L2 は端のデータビット、つまり符号の境界だと前回説明した。しかし1行目を見ると D0 D1 L1という記述があることに気づくだろう。
In [14]: dem = circuit.detector_error_model( )
In [15]: dem
Out[15]:
stim.DetectorErrorModel('''
error(0.1) D0 D1 L1
error(0.116) D0 D2
error(0.1) D0 L0
error(0.116) D1 D3
error(0.1) D1 L2
error(0.02) D2 D3 L1
error(0.02) D2 L0
error(0.02) D3 L2
repeat 31 {
error(0.02) D2 D4
error(0.02) D3 D5
error(0.02) D4 D5 L1
error(0.02) D4 L0
error(0.02) D5 L2
shift_detectors 2
}
error(0.02) D2 D4
error(0.02) D3 D5
error(0.02) D4 D5 L1
error(0.02) D4 L0
error(0.02) D5 L2
''')
L<数字>は符号の境界であるとともに、OBSERVABLE_INCLUDE で指定したデータ量子ビットに対応する。D0 D1 L1は辺D0-D1で+1のシンドロームがマッチした場合、L1の量子ビットを反転するとよいことを示している。全ての実験が終わってから復号するバッチ復号の場合、L1が何回反転を必要したかを数えておき、奇数回の場合にデータの訂正操作(測定値の読み替え)を行うこととなる。
In [16]: print( dem.diagram("matchgraph-svg") )
Warning: not all detectors had coordinates. Placed them arbitrarily.

復号グラフを図で表示してみる。見やすさのために繰り返し回数は2回とした。検出器の場所が指定されていないため、左上から三角形を描くように検出器が疑2次元的に並べられている。正しいエラーグラフは前回(#2)示したため、今回は座標指定はしない。
反復符号の性能を評価する
論理エラー率の算出
論文でよくみられるような、符号の性能を評価してみる。繰り返し回数はとりあえず31回だ。検出器が最初の1ステップ、繰り返し31ステップ、最後の終端処理で33ステップだけ回路に置かれ、33 × ( d - 1 ) 個の検出器が並ぶことになる。
In [17]: import pymatching
...: dem = circuit.detector_error_model( decompose_errors = False )
...: matcher = pymatching.Matching.from_detector_error_model( dem )
...: sampler = circuit.compile_detector_sampler( )
In [18]: num_shots = 8_192
...: derr, obs = sampler.sample( shots = num_shots, separate_observables = True )
In [19]: predictions = matcher.decode_batch( derr )
In [20]: predictions
Out[20]:
array([[1, 1, 1],
[0, 0, 0],
[0, 1, 1],
...,
[1, 1, 0],
[0, 0, 0],
[0, 0, 1]], dtype=uint8)
チュートリアル[1]を見ると、復号グラフを生成する際に、decompose_errors = True としているが、あまり意味が分からないため False にしておく(In[17])。サンプリング回数 num_shots はどれだけ小さなイベントを見たいかによって変えたほうがよい。論理エラー率 p_L を与える確率分布が二項分布に従っているとすると、分散の平方根は sqrt(( 1 - p_L ) p_L / num_shot ) 程度なので見たいエラー率の 1/3 程度ぐらいにしておく(適当)。
検出器モードでシミュレーションし (In[18])、復号器にシミュレーション結果を入力する(In[19])。前回とは異なり多数の試行回数のシンドロームを一度に復号できる decode_batch() を用いた。反転すべきビット情報が predictions に得られる (Out[20])。
In [21]: (predictions ^ obs)[:20,:]
Out[21]:
array([[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[1, 1, 1],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[1, 1, 1],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0]], dtype=uint8)
In [22]: numpy.sum( predictions ^ obs, axis = 0)[0] / num_shots
Out[22]: 0.135498046875
データ量子ビットの観測値 obs と 推定値 predictions の排他的論理和(XOR)を計算すると、データ量子ビットの観測値が訂正される(Out[21])。データを眺めてみれば分かるように、訂正結果は必ず論理0( = 000)または論理1( = 111)となっていることに違和感を持つが、こうなるように符号とシンドロームが生成されている。チュートリアルでは、OBSERVABLE_INCLUDEが全てのデータ量子ビットではなく、1つだけを用いて評価しているのはこのためである。データを列方向に足し上げて num_shots で割ると論理エラー率が得られる(In[22])。
論理エラー率の物理エラー率依存性
少しコードが長くなってしまうが、回路生成 gen_circuit() と論理エラー率を計算する find_error_rate() を定義しておく。回路生成時には反復符号の符号距離 distance、初期化エラー p_init、観測エラー p_meas、ループ内繰り返し回数 num_repeat を指定できる。In [..]: が煩わしいかもしれないが、コピー&ペーストせずに自分のプログラムを書いて欲しい。
In [23]: import stim
...: import pymatching
...: import numpy
...:
...: def gen_circuit( distance, p_init, p_meas, num_repeat ):
...: d = distance
...: circuit = stim.Circuit()
...: circuit.append( 'R', [ i for i in range( 2 * d - 1 ) ])
...: circuit.append( 'X_ERROR', [ i for i in range( 2 * d - 1 ) ], p_init )
...: circuit.append( 'TICK' )
...: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2 ) ])
...: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2, 0, -1 ) ])
...: circuit.append( 'TICK' )
...: circuit.append( 'DEPOLARIZE1', [ i for i in range( 2 * d - 1 ) ], p_meas )
...: circuit.append( 'MR', [ 2 * i + 1 for i in range( d - 1 )] )
...: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( d - 1 ) + i ) ] )
...: circuit.append( 'TICK' )
...: detector_block_text = ''
...: for i in range( d - 1 ):
...: detector_block_text \
...: += 'DETECTOR rec[{0}] rec[{1}]\n'.format( -( d - 1 ) * 2 + i ,
...: -( d - 1 ) + i )
...: repeat_block_text = '''
...: CNOT {0}\n CNOT {1} \n TICK
...: DEPOLARIZE1({5}) {2} \n MR {3}
...: {4}\n TICK
...: '''.format(
...: ' '.join( [ str( i ) for i in range( 2 * d - 2 ) ] ),
...: ' '.join( [ str( i ) for i in range( 2 * d - 2, 0, -1 ) ] ),
...: ' '.join( [ str( i ) for i in range( 2 * d - 1 ) ] ),
...: ' '.join( [ str( 2 * i + 1 ) for i in range( d - 1 )]),
...: detector_block_text,
...: p_meas )
...: circuit.append_from_stim_program_text( 'REPEAT {0} {{\n{1}\n}}'.format( num_repeat, repeat_block_text ))
...: circuit.append( 'MR', [ 2 * i for i in range( d )] )
...: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( 2 * d - 1 ) + i ),
...: stim.target_rec( - ( d ) + i ),
...: stim.target_rec( - ( d ) + i + 1 ) ] )
...: for i in range( d ):
...: circuit.append( 'OBSERVABLE_INCLUDE', [ stim.target_rec( - d + i ) ], i )
...:
...: return circuit
In [24]: def find_error_rate( circuit, num_shots ):
...:
...: dem = circuit.detector_error_model( decompose_errors = False )
...: matcher = pymatching.Matching.from_detector_error_model( dem )
...: sampler = circuit.compile_detector_sampler( )
...:
...: derr, obs = sampler.sample( shots = num_shots, separate_observables = True )
...: predictions = matcher.decode_batch( derr ) ### changeed
...: return numpy.sum( predictions ^ obs, axis = 0)[0] / num_shots
チュートリアル[1]では、繰り返しループ回数を符号距離の3倍としていた。ここではその値を用いる。初期化のエラーがなく、符号距離3、測定エラー率 3 % の場合には論理エラー率が 3.7 % であった。
In [25]: circuit = gen_circuit( 3, 0.0, 0.03, 3 * 3 ) # 3 * d
In [26]: find_error_rate( circuit, 8_192 )
Out[26]: 0.037353515625
3 * d回繰り返しを行った際の論理エラー率と測定エラー率(=初期化エラー率)の関係をグラフ化する。符号距離 d については d - 1が2, 4, 8, 16, 32となるように設定した (In[28])。初期化のエラーは測定のエラーと同じ値を用い、測定のエラーと初期化のエラーなどまとめて物理エラー率と呼ぶことにする。
In [27]: import matplotlib.pylab as pl
...: phys_error_rates = numpy.linspace( 0, 0.2, 21 )[ 1 : ]
...: num_shots = 8_192
In [28]: for distance in [ 3, 5, 9, 17, 33 ]:
...: logical_error_rates = [ ]
...: for p_meas in phys_error_rates:
...: circuit = gen_circuit( distance, p_meas, p_meas, 3 * distance )
...: p_L = find_error_rate( circuit, num_shots )
...: logical_error_rates.append( p_L )
...: pl.plot( phys_error_rates, logical_error_rates, label = 'distance = {}'.format( distance ))
...: pl.plot( phys_error_rates, phys_error_rates, label = 'p_L = p_physical' )
...: pl.grid()
...: pl.legend()
...: pl.savefig( '1.svg' )

それぞれの符号距離に対する論理エラー率の線が交差する点をしきい値と呼び、今回のエラーモデルでは 16 % 程度となった。しきい値より小さな物理エラー率の場合、物理エラー率が同じであれば符号距離を大きくすることで論理エラー率を抑制できる。
p_L = p_physical の線は(3 * d回繰り返した場合の論理エラー率)=(物理エラー率)である線を表わしている。この線より上側の領域では、物理エラー率より3 * d回繰り返し時の論理エラー率が増えている。エラー訂正することにより物理エラー率より論理エラー率が大きくなった場合を損、エラー訂正することにより物理エラー率より論理エラー率が小さくなった場合を益とし、この線を損益分岐点と呼ぶことにする。それぞれの符号距離に対する損益分岐点は、直線と論理エラー率との交点を読み取ればよいため、d = 9程度の符号で物理エラー率が 9 %、d = 5だと 6 %、d = 3 だと 2% であることが分かる。(3 * d ラウンドの論理エラー率) < (物理エラー率) とし、誤りが訂正のご利益を得るためには、それぞれの符号距離に対応する損益分岐点以下の物理エラー率における実装が要求される。
In [29]: phys_error_rates = numpy.logspace( -2,-0.52, 21 )
In [30]: for distance in [ 3, 5, 9, 17, 33 ]:
...: logical_error_rates = []
...: for p_meas in phys_error_rates:
...: circuit = gen_circuit( distance, p_meas, p_meas, 3 * distance )
...: p_L = find_error_rate( circuit, num_shots )
...: logical_error_rates.append( p_L )
...: pl.loglog( phys_error_rates, logical_error_rates, label = 'distance = {}'.format( distance ))
...: pl.loglog( phys_error_rates, phys_error_rates, label = 'p_L = p_physical' )
...: pl.grid()
...: pl.legend()
...: pl.savefig( '1.svg' )
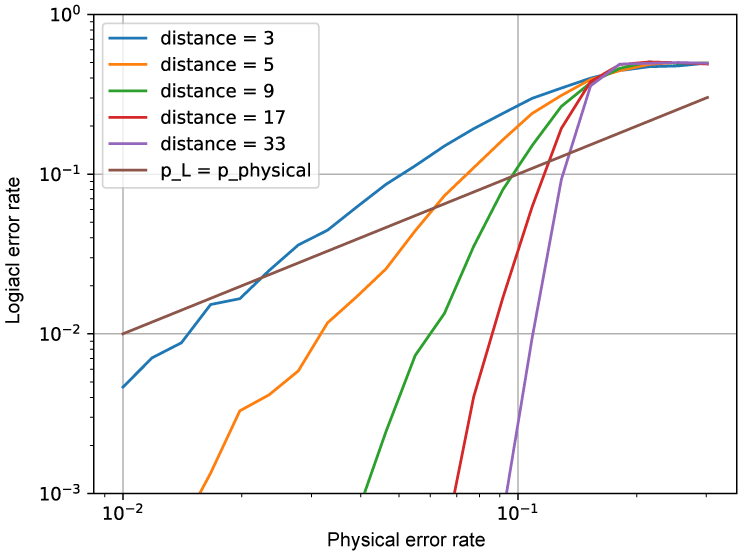
両対数グラフを描くと、エラー率が小さな領域が見やすくなる。今回は8192回シミュレーションを行ったため、論理エラー率 0.1 %の場合の標準偏差は 0.03 %である。小さな論理エラー率を正しく評価しようとすると、シミュレーション回数を増やすしかない。
論理エラー率の繰り返し回数依存性
先ほどは繰り返し回数を符号距離 d の3倍 d * 3に設定した(チュートリアル通り)。繰り返し回数を変えながら論理エラー率を評価するとどのようになるだろうか。誤り訂正符号を実装する上では1回のシンドローム測定ごとの論理エラー率が知りたい情報である。符号距離 3、5、9の場合の繰り返し回数ごとの論理誤り率依存性を計算する。ここで初期化のエラー率を 10 %、測定のエラーを3%とした。
In [31]: p_init = 0.10
...: p_meas = 0.03
...: num_shots = 64_536
...: repeats = numpy.arange( 1, 63, 1 )
In [32]: for distance in [ 3, 5, 9 ]:
...: logical_error_rates = []
...: for repeat in repeats:
...: circuit = gen_circuit( distance, p_init, p_meas, repeat )
...: p_L = find_error_rate( circuit, num_shots )
...: logical_error_rates.append( p_L )
...: pl.plot( repeats, logical_error_rates, label = 'distance = {}'.format( distance ))
In [33]: pl.grid()
...: pl.legend()
...: pl.savefig( '1.svg' )

初期化のエラーに関しては、誤り訂正の繰り返しを続けたからといって良くなるわけではないことが分かる。その一方で符号距離が大きくなるほど初期化のエラー率が小さくなっており、よりきれいな初期状態が生成されていることがわかる。もう少し繰り返し回数を大きくして論理エラー率を計算してみる。繰り返し回数が指数的に大きくなるように対数で等間隔になるようにサンプリングする (In[34])。符号距離が大きくなると論理エラー率が小さく、より大きな繰り返し回数まで見たくなる。
In [34]: p_init = 0.10
...: p_meas = 0.03
...: num_shots = 4_096
...: repeats = numpy.array( [ round( x ) for x in numpy.logspace( 0, 3.2, 31 )], dtype = int )
...: vault = []
In [35]: for distance, mult in zip([ 3, 5, 9 ], [ 1, 6, 55 ]):
...: logical_error_rates = []
...: for repeat in repeats:
...: circuit = gen_circuit( distance, p_init, p_meas, repeat * mult )
...: p_L = find_error_rate_single( circuit, num_shots )
...: logical_error_rates.append( p_L )
...: pl.semilogx( repeats * mult, logical_error_rates, label = 'distance = {}'.format( distance ))
...: vault.append(( distance, mult, logical_error_rates ))
In [36]: pl.ylabel( 'Logical error rate' )
...: pl.xlabel( '# of repetition' )
...: pl.grid()
...: pl.legend()
...: pl.savefig( '1.svg' )
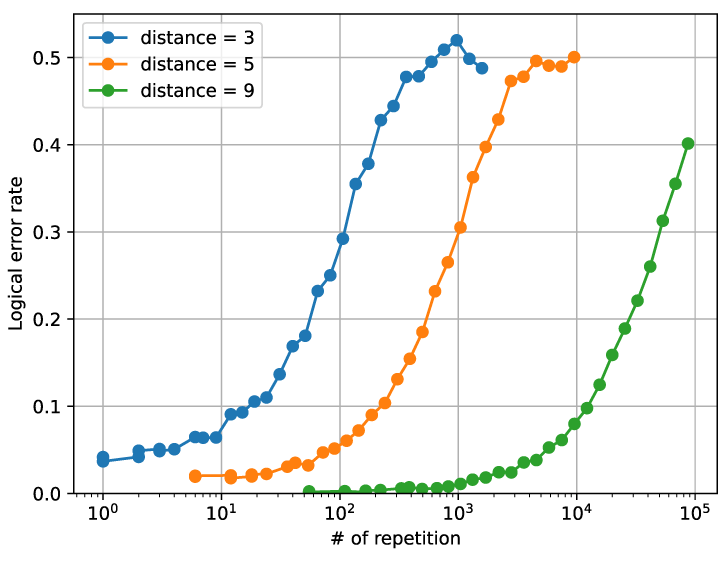
この片対数グラフ図を見てこれが指数減衰する曲線だと気づいた人は、そこそこの経験者だろう。指数減衰であれば論理エラー率は 1 - ((1-p_L) ^ num_repeat) に従うはずである。これが指数減衰であることが確認できれば、論理エラー率が小さな場合には、テイラー展開を用いて1回の繰り返しあたりの論理エラー率を p_L * num_repeat と近似的に簡便に表現できる。減衰曲線が本当に指数的に減衰しているのかどうか、フィッティングにより確かめてみる。
論理初期化のエラー p_Li による論理エラー率のオフセットを考慮し、最終的に p_L = 0.5 に緩和するモデルをフィッティングに採用した (In[37])。途中で大きな数のべき乗でエラーがでてしまったので、繰り返し回数を mult 分だけ縮尺を小さくしてフィッティングし、1回路の繰り返し当たりの論理エラー率 p_Lr を得る際に (In[38]の5行目) 縮尺を元に戻している。指数減衰を暗に仮定したズルであるが許して欲しい。
In [37]: logical_error_decay = lambda k, p_Li, p_Lr : - 0.5 * ( 1 - p_Li ) * (( 1 - p_Lr ) ** k ) + 0.5
...: import scipy.optimize
In [38]: for distance, mult, logical_error_rates in vault:
...: result, cov = scipy.optimize.curve_fit( logical_error_decay, repeats, logical_error_rates, [ 0, 0.01 ])
...: p_Li = result[ 0 ]
...: p_Lr = result[ 1 ] / mult
...: pl.semilogx( repeats * mult, logical_error_rates, 'o', label = 'distance = {}'.format( distance ))
...: pl.semilogx( repeats * mult, logical_error_decay( repeats * mult, p_Li, p_Lr), '-', label = 'distance = {}'.format( distance ))
In [39]: pl.grid()
...: pl.ylabel( 'Logical error rate' )
...: pl.xlabel( '# of repetition' )
...: pl.legend()
...: pl.savefig( '1.svg' )

モデル曲線がよくデータに乗っていることがわかり、論理エラー率は繰り返しごとに指数関数的に減衰していることが分かる(そう仕向けたせいでもあるが)。フィッティングにより得られた論理ビットの初期化のエラー率 p_Liと 1回の繰り返しあたりの論理エラー率 p_Lr をまとめると下の表のようになる。
| d | p_Li | p_Lr |
|---|---|---|
| 3 | 7.69 % | 0.78 % |
| 5 | 2.71 % | 0.090 % |
| 9 | 0.33 % | 18 ppm |
論理エラー率が小さいため、全体の論理エラー率は (繰り返し1回あたりの論理エラー率) x (繰り返し回数)となるはずである。しきい値を計算したグラフで符号距離5の論理誤り率は約 1 %であり、符号距離の3倍を要しているので15で割ると0.06 % となる。初期のエラー率の仮定が3%と10%とで異なるため完全一致はしないが、おおむね d = 5 の1回あたりのエラー率 0.09 % と一致する。
稀なシンドロームのパターン
確率が低い場合に論理エラーを生じるパターンに興味がある。物理エラー率が低いにも関わらず、論理エラー率が生じてしまうようなシンドロームのバターンとはどのようなものであろうか。いわゆるエラーが鎖状に繋がっており、検出器が1となるホットシンドロームを復号で間違ってしまうパターンを体感したい。
符号距離17で物理エラー率を 3 %、繰り返し回数を符号距離の3倍に設定。先のしきい値を示す両対数のグラフにおいて、d=17の場合は物理エラー率が 7 % の場合に論理エラー率が 0.1 %であった。論理エラー率は物理エラー率が η 倍になった際に、しきい値以下では論理エラー率が η^((d-1)/2) 程度になる。今の場合物理エラー率が 1/2.3 となっているため、論理エラー率は 1e-3 * (1/2.3)^8 = 1e-6となることが期待される。num_shots を 2^20 (~10^6)としてシミュレーションを行った(In[40])。実際はこの回数でも足りず、何回か実行してエラーを生じた場合を見つけたことは内緒にしておこう。
In [40]: distance = 17
...: p_meas = 0.03
...: num_shots = 1_048_576
In [41]: circuit = gen_circuit( distance, p_meas, p_meas, 3 * distance )
...: dem = circuit.detector_error_model( decompose_errors = False )
...: matcher = pymatching.Matching.from_detector_error_model( dem )
...: sampler = circuit.compile_detector_sampler( )
In [42]: derr, obs = sampler.sample( shots = num_shots, separate_observables = True )
...: predictions = matcher.decode_batch( derr ) ### changeed
100万回シミュレーションして1回だけエラーとなる例が得られた(ことにしておこう)。観測値 (Out[44])と推定値(Out[45])が間違っていることが確認できる。この時の検出器の値(シンドローム値)をグラフに表示する (In[46])。復号の話をする前に、復号に用いるエラーモデルを表示する (Out[47])。長いので繰り返しの部分だけ表示し、少しコメントを入れている。
In [43]: numpy.where( 1 == ( predictions ^ obs )[ :, 0 ])
Out[43]: (array([1047881], dtype=int64),)
In [44]: numpy.array( obs[ 1047881 ], dtype = int )
Out[44]: array([1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0])
In [45]: predictions[ 1047881 ]
Out[45]: array([0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1], dtype=uint8)
In [46]: pl.pcolor( derr[1047881].reshape((53,16)).T );
...: pl.xlabel( 'Repetition index (time)' )
...: pl.ylabel( 'Detector index (in space)' )
...: pl.savefig( '1.svg' )
In [47]: dem
Out[47]:
stim.DetectorErrorModel('''
(...skip...)
repeat 50 {
error(0.02) D16 D32 # READOUT ERROR
error(0.02) D17 D33
error(0.02) D18 D34
error(0.02) D19 D35
error(0.02) D20 D36
error(0.02) D21 D37
error(0.02) D22 D38
error(0.02) D23 D39
error(0.02) D24 D40
error(0.02) D25 D41
error(0.02) D26 D42
error(0.02) D27 D43
error(0.02) D28 D44
error(0.02) D29 D45
error(0.02) D30 D46
error(0.02) D31 D47
error(0.02) D32 L0
error(0.02) D32 D33 L1 # DATAQUBIT EROR
error(0.02) D33 D34 L2
error(0.02) D34 D35 L3
error(0.02) D35 D36 L4
error(0.02) D36 D37 L5
error(0.02) D37 D38 L6
error(0.02) D38 D39 L7
error(0.02) D39 D40 L8
error(0.02) D40 D41 L9
error(0.02) D41 D42 L10
error(0.02) D42 D43 L11
error(0.02) D43 D44 L12
error(0.02) D44 D45 L13
error(0.02) D45 D46 L14
error(0.02) D46 D47 L15
error(0.02) D47 L16
shift_detectors 16
}
(...skip...)
''')
復号グラフの中で検出器の番号が大きく変わる辺はそれぞれの繰り返し毎に生じる測定エラーを検出するものである。また番号が一つ変わる辺はデータ量子ビットのエラーを示している。測定のエラーについては L<数字>が無いために、復号時にホットシンドローム(+1の検出器の値)がペアを組んでもデータ量子ビットの値を変更する必要がない。その一方で、データ量子ビットにエラーが生じた場合、ホットシンドロームが辺を使って(必ずしも1つでなくてもよい)ペアを組んだ場合には、L<数字>のデータ量子ビットの値を反転する必要がある。
今回は、測定のエラーもデータ量子ビットのエラーも、同じエラー率 0.02 がそれぞれの辺に割り当てられていることに注意されたい。どちらの辺を使ってペアを組んだとしても同じコストであるため、辺を何度飛び越えるかという回数(マンハッタン距離)がペアを行うためのコスト値となる。全体的に低コストになるように、ホットシンドロームのペアを作ることが復号である。
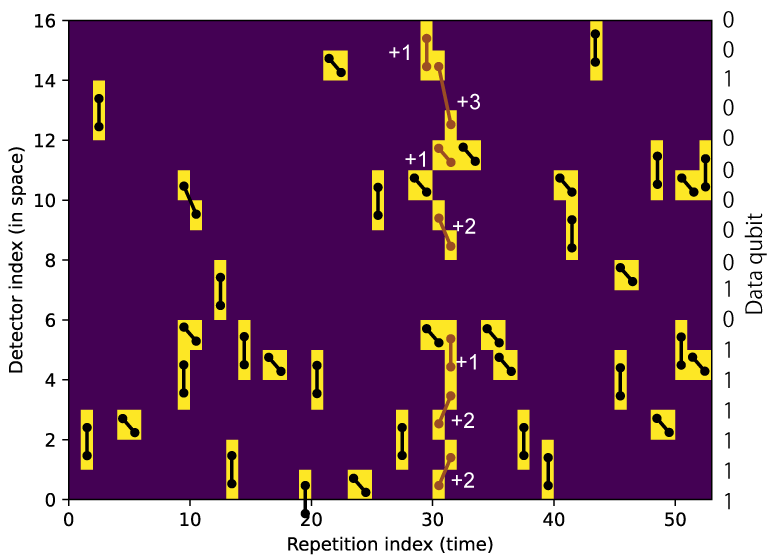
縦軸に検出器の空間方向の番号(インデックス)を示す。実際に検出器の番号は16ヶの検出器を53回繰り返すように配置されているため、(検出器の番号) mod 16 が示されている。横軸は繰り返し回数を示す。最初の1回と17x3=51回の繰り返しとデータ量子ビットの測定値を用いて使った最後の1回とで0~52番が示されている。図中のダンベルマークで頭の中で復号した結果を示す。黒色のダンベルマークは比較的簡単なものであり、周囲にホットシンドロームが無く、隣接するもの(辺の長さ+1)または斜め方向のペア(辺の長さ2)でペアが作られている。グラフの右端にデータ量子ビットの測定値を表示している。
- 繰り返しインデックス9番、検出器インデックス9と10番のホットシンドロームは、データ量子ビットのエラーが起きた直後に測定のエラーが生じたため、斜め方向にエラー鎖が伸びている。
- 繰り返しインデックス19番、検出器インデックス0番のホットシンドロームは、復号グラフの端(L0)とペアを組んでいる。
- 繰り返しインデックス12番、検出器インデックス6と7番のペアはデータ量子ビットQ14の反転を意味している (データ量子ビットは0,2,4,6,..と偶数で番号が付けられていることに注意されたい)。この時繰り返しインデックス45-46、検出器インデックス7のホットシンドロームのは測定エラーの辺を用いてペアを作っているためデータ量子ビットの反転に寄与しない。
難しい箇所は繰り返しインデックスが30周辺の箇所である。赤色のダンベルに注目されたい。検出器番号13-16周辺のホットシンドロームが3つあり、符号の境界(L16)とペアを組まないとすると、距離が3だけ離れた検出器番号12とペアを組むしかなくなる。このペアは2つのデータ量子ビット (Q26とQ28) の反転と測定検出器12または14の測定エラーが同時に生じたケースである。ともに物理エラー率を3%とすると 3%^3 = 2.6e-5 程度しか生じないケースである。赤色のダンベルのマークに関するコストを足し上げると+12となる。
しかし同じコストで上のようなケースも考えられる。データ量子ビットの3回同時反転が繰り返しインデックス31、検出器番号5と8で生じたと考えるケースである。この場合もこのような長距離のペアを組まないと、ペアを組まないホットシンドロームが生じてしまう。恐らく Pymatching による復号器は同じコストであるためこちらのケースを採用し、論理エラーを生じてしまったと考えられる。
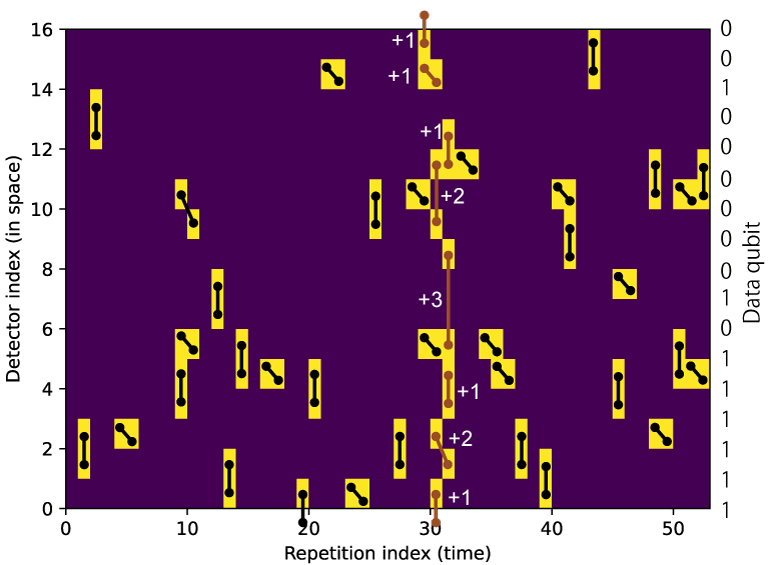
さらに物理エラー率を2%に下げて論理エラーを生じるパターンを下図に示す。手作業の復号様子をダンベルマークにより書き込んでいる。黒色は割と自明なペアであり、繰り返しインデックス30~32周辺の青色と赤色のダンベルマークが論理エラーを生じてしまったのだと考えられる。図の右端にデータ量子ビットの測定値を記載している。この測定値の様子から青色が正しい復号を与えるペアの作り方であることが分かり、その際の青色のコストは+12であった。その一方で同じコストで赤色のマークで示すようなホットシンドロームのペアも考えられる。Pymatchingは赤色のように推定し論理エラーを生じたのだと考えられる。

青色と黒色のペアを採用した場合に正しい推定となることを確認しておく。
- データ量子ビットQ0は、どのペアの橋の下をくぐらないのでエラーなし。
- データ量子ビットQ2は、繰り返しインデックス22の黒色ペアと、繰り返しインデックス33の青色ペアの下をくぐり、偶数回であるのでエラーは元通りとなりエラーなし。
- データ量子ビットQ6は、繰り返しインデックス33の青色ペアの下をくぐり、奇数回であるのでデータ量子ビットの反転操作が必要。
CNOTのエラーモデル
もう少しモデルを実装に近くするために、CNOTのエラーを考察する。引き続き(古典)反復符号を実装する。今回はIn[51]とIn[52]の箇所と繰り返し内In[54]のCNOTの直後にDEPOLARIZE2を入れた。DEPOLARIZE2は以前の 記事 #1 で紹介したとおり、指定した確率 p に対して15種類の2量子ビットパウリ反転が p/15 の確率で生じるものであった。今回はCNOTゲートの直後に追加し、確率 p_cnot でCNOTゲートにて生じるエラー源とする。またCNOTの対象ではないデータ量子ビットも同時に緩和するはずである。同じエラー率 p_cnot による分極解消エラーを追加した。
- CNOTのエラーのみに注目するため、初期化・観測のエラー率を0としてある (In[49])。
- 復号グラフのオブザーバブル
L<数字>の番号が量子ビットの番号に一致していなかったので微修正した (In[56])。-> しかしこれは、オブザーバブルの数が無駄に増えて無駄だったことが後に判明する。#4を参照。 - 復号グラフをきれいに作るため、
DETECTOR命令に検出器の場所を指定している。ループ内の座標のシフトSHIFT_COORDSには、append()ではなくappend_operation()を使わなくてはならないことが分かった (In[54])。
繰り返しブロックの平文記述回避
繰り返しブロックを平文でしか作れないはずはないと考え、[2] を調べていたところ、stim.CircuitRepeatBlock を見つけた。このクラスのインスタンスを作る際に繰り返し回数と繰り返しブロックの回路を定義することができる。
下記のプログラム中のIn[54]でループ内の処理を circuit_repeat に定義する。回路を定義した後に CircuitRepeatBlock をインスタンス化し、その際にループ回数を指定する (In[54]の最終行)。インスタンス化したオブジェクトは、そのままメインの回路 circuit.append( ) を使って追加することができる。
In [48]: import stim
...: import pymatching
...: import numpy
...: import matplotlib.pylab as pl
In [49]: p_init = 0.0
...: p_meas = 0.00
...: p_cnot = 0.03
...: distance = 3
...: num_repeat = 1
...:
In [50]: d = distance
...: circuit = stim.Circuit()
...: circuit.append( 'R', [ i for i in range( 2 * d - 1 )])
...: circuit.append( 'X_ERROR', [ i for i in range( 2 * d - 1 )], p_init )
...: circuit.append( 'TICK' )
In [51]: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2 )])
...: circuit.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2 )], p_cnot )
...: circuit.append( 'DEPOLARIZE1', [ 2 * d - 2 ], p_cnot )
In [52]: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2, 0, -1 ) ])
...: circuit.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2, 0, -1 ) ], p_cnot)
...: circuit.append( 'DEPOLARIZE1', [ 0 ], p_cnot)
In [53]: circuit.append( 'TICK' )
...: circuit.append( 'DEPOLARIZE1', [ i for i in range( 2 * d - 1 )], p_meas )
...: circuit.append( 'MR', [ 2 * i + 1 for i in range( d - 1 )] )
...: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( d - 1 ) + i ) ], [ i, 0 ] )
...: circuit.append( 'TICK' )
In [54]: circuit_repeat = stim.Circuit() # REPEAT BLOCK
...: circuit_repeat.append( 'CNOT', [ i for i in range( 2 * d - 2 ) ])
...: circuit_repeat.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2 ) ], p_cnot )
...: circuit_repeat.append( 'DEPOLARIZE1', [ 2 * d - 2 ], p_cnot )
...: circuit_repeat.append( 'CNOT', [ i for i in range( 2 * d - 2, 0, -1 ) ])
...: circuit_repeat.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2, 0, -1 ) ], p_cnot )
...: circuit_repeat.append( 'DEPOLARIZE1', [ 0 ], p_cnot)
...: circuit_repeat.append( 'TICK' )
...: circuit_repeat.append( 'DEPOLARIZE1', [ i for i in range( 2 * d - 1 ) ], p_meas )
...: circuit_repeat.append( 'MR', [ 2 * i + 1 for i in range( d - 1 )])
...: circuit_repeat.append_operation( 'SHIFT_COORDS', [], [ 0, 1 ] )
...: for i in range( d - 1 ):
...: circuit_repeat.append( 'DETECTOR', [ stim.target_rec( - ( d - 1 ) * 2 + i ),
...: stim.target_rec( - ( d - 1 ) + i ) ], [ i, 0 ] )
...: circuit_repeat.append( 'TICK' )
...: circuit.append( stim.CircuitRepeatBlock( repeat_count = num_repeat, body = circuit_repeat ))
In [55]: circuit.append( 'MR', [ 2 * i for i in range( d )] )
...: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( 2 * d - 1 ) + i ),
...: stim.target_rec( - ( d ) + i ),
...: stim.target_rec( - ( d ) + i + 1 ) ], [ i, 1 ] )
In [56]: for i in range( d ):
...: circuit.append( 'OBSERVABLE_INCLUDE', [ stim.target_rec( - d + i )], 2 * i )
...:
この量子回路と、復号グラフを表示する。きちんとファイルに出力されるように改善した(以前は画面にSVGファイルの中身が表示されていた。また復号のエラーモデルを出力しておく。
In [57]: with open('circuit.svg', 'w' ) as f:
...: print(circuit.diagram( 'timeline-svg' ), file=f )
In [58]: dem = circuit.detector_error_model()
...: with open( 'decode_graph.svg', 'w' ) as f:
...: print( dem.diagram( 'matchgraph-svg' ), file = f )
In [59]: dem
Out[59]:
stim.DetectorErrorModel('''
error(0.00806504) D0 D1 L2
error(0.016) D0 D2
error(0.016) D0 D3 L2 # <----------- LOOK
error(0.00806504) D0 L0
error(0.016) D1 D3
error(0.0277424) D1 L4
error(0.016) D2 D3 L2
error(0.016) D2 D4
error(0.016) D2 D5 L2 # <----------- LOOK
error(0.03536) D2 L0
error(0.016) D3 D5
error(0.03536) D3 L4
error(0.00806504) D4 D5 L2
error(0.0277424) D4 L0
error(0.00806504) D5 L4
detector(0, 0) D0
detector(1, 0) D1
shift_detectors(0, 1) 0
detector(0, 0) D2
detector(1, 0) D3
detector(0, 1) D4
detector(1, 1) D5
''')
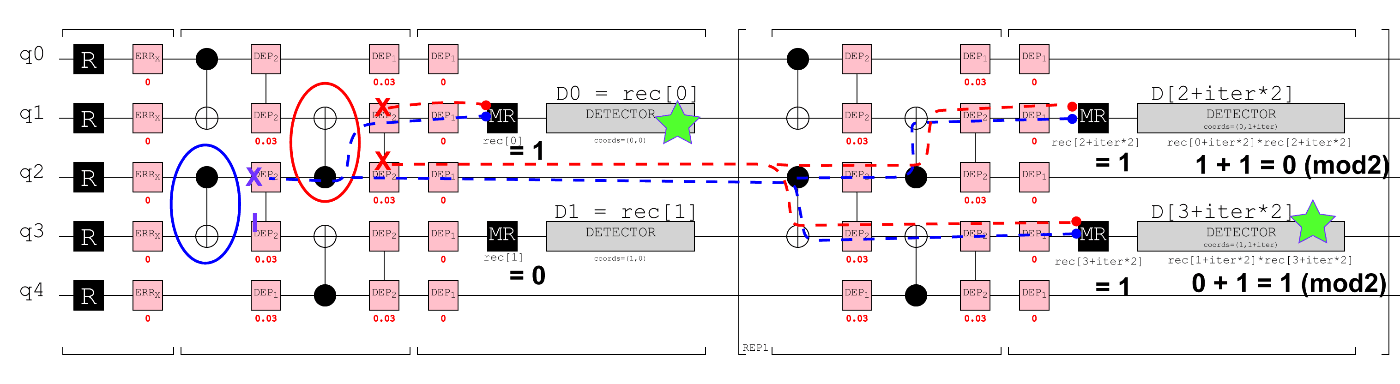
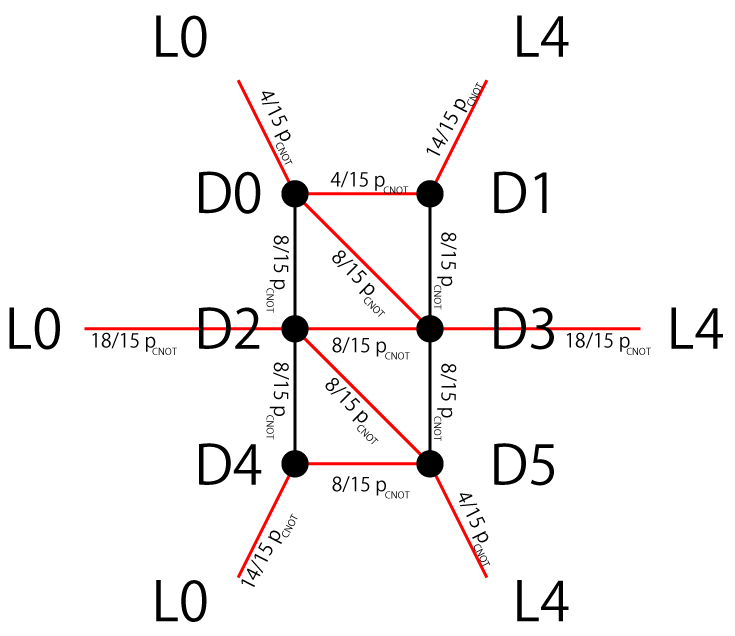
辺の色についてStimのドキュメントに次の記載があった。赤色の辺はデータ量子ビットに反転を生じ、黒色の辺はデータ量子ビットに反転がない。上の復号グラフにおいて L<数字>が無い辺は黒色の線となり、アンシラ量子ビットのエラーを意味する。
実際のところ、辺 D2-L0 や辺D1-L4はぴったり 18/15 p_cnot や 14/15 p_cnot の値に一致するわけではない。CNOTのエラー率 p_cnot を小さくすると漸近的にそれらの値に収束するため、p_cnot^2 の効果が取り込まれているようである。しかしどのような過程が入っているのか解析できなかった。力不足である。
時空間エラー
復号グラフを見ると、今までにはなかったD0からD3への斜めの線が入っていることが分かる。Out[59]より、D0-D3はL2の反転を伴って p_cnot * (8/15)の確率で生じるエラーであることがわかる。この復号グラフの辺D0-D3は、回路図中の青色で印をつけたCNOT(2-3)と赤色で印をつけたCNOT(1-2)の特定の成分が寄与する。
2量子ビットの分極解消雑音のそれぞれの成分がどの検出器をクリックしているのか下の表にまとめた。確率は全て p_cnot / 15 である。
Q2-Q3のCNOT直後のエラー伝搬
| I (Q3) | X | Y | Z | |
|---|---|---|---|---|
| I (Q2) | IX (D1-D3) | IY (D1-D3) | IZ | |
| X | XI (D0-D3) | XX (D0-D1) | XY (D0-D1) | XZ (D0-D3) |
| Y | YI (D0-D3) | YX (D0-D1) | YY (D0-D1) | YZ (D0-D3) |
| Z | ZI | ZX (D1-D1) | ZY (D1-D3) | ZZ |
Q1-Q2のCNOT直後のエラー伝搬
| I (Q2) | X | Y | Z | |
|---|---|---|---|---|
| I (Q1) | IX (D2-D3) | IY (D2-D3) | IZ | |
| X | XI (D0-D2) | XX (D0-D3) | XY (D0-D3) | XZ (D0-D2) |
| Y | YI (D0-D2) | YX (D0-D3) | YY (D0-D3) | YZ (D0-D2) |
| Z | ZI | ZX (D2-D3) | ZY (D2-D3) | ZZ |
Q2-Q3のCNOT直後のXIエラー成分(Q2の単純な反転、YI、XZ、YZも同様)は、その直後の検出器D0では検出されるものの、CNOTの印加タイミング後であるため検出器D1では検出されず、検出器D3により検出される(青色の点線)。このため復号グラフが斜め(space-time)となり、p_cnot / 15の4パターンで4倍のエラーが設定される。
Q1-Q2のCNOT直後のXXエラー成分はQ1とQ2で同時にX反転が生じる(XY, YX, YYも同様)場合である。Q1のエラーは直後の測定と検出器 D0 によりエラーが検出されるが、Q2のエラーは1サイクル遅れ、検出器 D2 直前の測定 rec[2]と検出器 D3 の直前の測定 rec[3]が +1 となる(赤色の点線)。検出器 D2 は D2 直前の測定結果 (rec[2]=1) と D0 直前の測定結果 (rec[0]=1) の排他的論理和 (XOR) の結果によりシンドロームが生成されるため、検出器D2にホットシンドロームは生じない。検出器 D3ではQ2の反転エラーを検出する。このため復号グラフの辺D0-D3にp_cnot / 15 × 4パターンのエラー率が与えられる。
二つのCNOTのパターンのエラー確率の和が p_cnot / 15 x 8のエラー率を与えている。実際の誤り訂正の実装時には、CNOTのエラー率が全てのエラー成分に対して等方的とは限らない。事前に分かっているエラー率や、エラー成分の偏りを設定することで (下記 PAULI_CHANNEL_2を参照)、復号時の誤ったペア生成を避けて論理エラー率を小さくすることに貢献する。これを複合器のチューニングと呼ぶことにする。
復号グラフの確認
エラー伝搬の様子を回路から調べるのが面倒であれば、15個のパウリ成分一つ一つを下記のように設定することができる。
circuit.append( 'PAULI_CHANNEL_2', [ 1, 2 ], [ 0, 0, 0, 0.1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ] )
2つ目の引数に対象となる量子ビットを指定し、次の引数は15種類のエラー率を IX、IY、IZ、XI、XX、XY、XZ、YI、YX、YY、YZ、ZI、ZX、ZY、ZZ の順番で設定する。下の例では Q1 Q2 に対して p_XI の反転確率を 10 % で設定している。量子ビットを [ 1, 2 ] と指定した場合の XI と 量子ビットを [ 2, 1 ] と指定した場合のIXが同じ意味となるため、指定する量子ビットの順番に注意する必要がある。これらをIn[51]やIn[52]のDEPOLARIZE2の代わりに用い、ほかのエラー率をゼロにして、復号グラフの様子を眺めるながら確認を行った。
エラーが後段にどのように伝搬していくのか知りたい際には、阪大の藤井大先生の量子計算超入門[3]の31ページを参考にされたい。次の本 [4] も参考になる。
論理エラー率の評価
CNOTエラー率を含んだ反復符号の論理エラー率を評価する。一般的には観測のエラー p_measと 2量子ビットゲートのエラー p_cnot を同じ値とし、物理量子ビットエラー率 p_physical として評価が行われている。しかし実装の際には、p_cnotとp_measが同じとは限らない。この様子を観察してみる。
エラーを含むCNOTを用いた反復符号を生成する回路 gen_circuit()と、回路をシミュレーションし、シンドローム結果から論理エラー率を計算する手続き find_error_rate() を示す。
In [60]: def gen_circuit( distance, p_init, p_meas, p_cnot, num_repeat ):
...:
...: d = distance
...: circuit = stim.Circuit()
...: circuit.append( 'R', [ i for i in range( 2 * d - 1 ) ])
...: circuit.append( 'X_ERROR', [ i for i in range( 2 * d - 1 ) ], p_init )
...: circuit.append( 'TICK' )
...: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2 ) ])
...: circuit.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2 ) ], p_cnot )
...: circuit.append( 'DEPOLARIZE1', [ 2 * d - 2 ], p_cnot )
...: circuit.append( 'CNOT', [ i for i in range( 2 * d - 2, 0, -1 ) ])
...: circuit.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2, 0, -1 ) ], p_cnot)
...: circuit.append( 'DEPOLARIZE1', [ 0 ], p_cnot)
...: circuit.append( 'TICK' )
...: circuit.append( 'DEPOLARIZE1', [ i for i in range( 2 * d - 1 ) ], p_meas )
...: circuit.append( 'MR', [ 2 * i + 1 for i in range( d - 1 )] )
...: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( d - 1 ) + i ) ], [ i, 0 ] )
...: circuit.append( 'TICK' )
...:
...: circuit_repeat = stim.Circuit()
...: circuit_repeat.append( 'CNOT', [ i for i in range( 2 * d - 2 ) ])
...: circuit_repeat.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2 ) ], p_cnot )
...: circuit_repeat.append( 'DEPOLARIZE1', [ 2 * d - 2 ], p_cnot )
...: circuit_repeat.append( 'CNOT', [ i for i in range( 2 * d - 2, 0, -1 ) ])
...: circuit_repeat.append( 'DEPOLARIZE2', [ i for i in range( 2 * d - 2, 0, -1 ) ], p_cnot )
...: circuit_repeat.append( 'DEPOLARIZE1', [ 0 ], p_cnot)
...: circuit_repeat.append( 'TICK' )
...: circuit_repeat.append( 'DEPOLARIZE1', [ i for i in range( 2 * d - 1 ) ], p_meas )
...: circuit_repeat.append( 'MR', [ 2 * i + 1 for i in range( d - 1 )] )
...: circuit_repeat.append_operation( 'SHIFT_COORDS', [], [ 0, 1 ] )
...: for i in range( d - 1 ):
...: circuit_repeat.append( 'DETECTOR', [ stim.target_rec( - ( d - 1 ) * 2 + i ),
...: stim.target_rec( - ( d - 1 ) + i ) ], [ i, 0 ] )
...: circuit_repeat.append( 'TICK' )
...: circuit.append( stim.CircuitRepeatBlock( repeat_count = num_repeat, body = circuit_repeat ))
...: circuit.append( 'MR', [ 2 * i for i in range( d )] )
...: for i in range( d - 1 ):
...: circuit.append( 'DETECTOR', [ stim.target_rec( - ( 2 * d - 1 ) + i ),
...: stim.target_rec( - ( d ) + i ),
...: stim.target_rec( - ( d ) + i + 1 ) ], [ i, 1 ] )
...: for i in range( d ):
...: circuit.append( 'OBSERVABLE_INCLUDE', [ stim.target_rec( - d + i ) ], 2 * i )
...:
...: return circuit
In [61]: def find_error_rate( circuit, num_shots ):
...: dem = circuit.detector_error_model( decompose_errors = False )
...: matcher = pymatching.Matching.from_detector_error_model( dem )
...: sampler = circuit.compile_detector_sampler( )
...:
...: derr, obs = sampler.sample( shots = num_shots, separate_observables = True )
...: predictions = matcher.decode_batch( derr )
...: return numpy.sum( predictions ^ obs, axis = 0)[0] / num_shots
初期化のエラーは無しとする。観測のエラー(待機時のデータ量子ビットのエラーを含む)とCNOTのエラー率を 0 から 10 % までそれぞれ掃引する (In[63])。論理エラー率を算出するために、2^13程度の回数のシミュレーションをそれぞれのエラー率に対して行う (In[64]) 。
このシミュレーション回数だと論理エラー率が 1 % のときに、その分散(の平方根)は 0.1 % 程度となる。下のプログラムの例は符号距離5であるが、符号距離3と9についても論理エラー率を調べた。
In [62]: from matplotlib.colors import LogNorm
...: p_init = 0.0
...: distance = 5
...: num_shots = 8_192
In [63]: p_meas_list = numpy.linspace( 0, .1, 41 )
...: p_cnot_list = numpy.linspace( 0, .1, 41 )
...: p_logical_grid = numpy.zeros(( len( p_meas_list ), len( p_cnot_list )))
In [64]: for i in range( len( p_meas_list )):
...: for j in range( len( p_cnot_list )):
...: p_meas = p_meas_list[ i ]
...: p_cnot = p_cnot_list[ j ]
...: circuit = gen_circuit( distance, p_init, p_meas, p_cnot, distance * 3 )
...: p_L = find_error_rate( circuit, num_shots )
...: p_logical_grid[ i ][ j ] = p_L if p_L < p_meas + 2 * p_cnot else 1e-6
In [65]: pl.pcolor( p_meas_list, p_cnot_list, p_logical_grid.T, norm = LogNorm( 1e-3, 0.15 ))
...: pl.colorbar()
...: pl.xlabel( 'Measurement error' )
...: pl.ylabel( 'Two-qubit gate (CNOT) error' )
...: pl.savefig( '1.svg' )
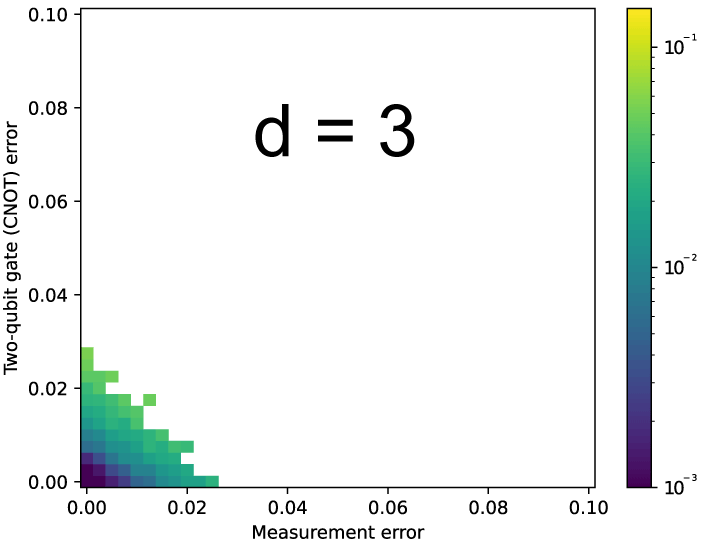

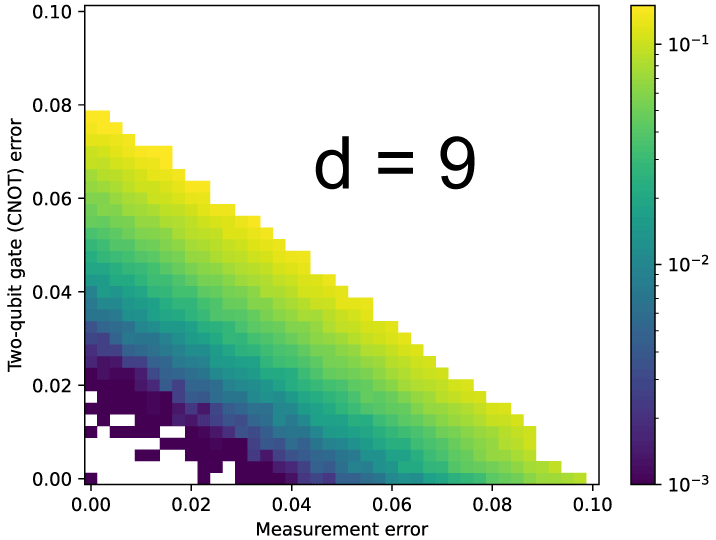
評価結果を上の3つの図に示す。図の描画の際に、(3 * d 回繰り返し時の論理エラー率) が繰り返し中に生じるエラー率 p_meas + p_cnot * 2 より大きな箇所は無効にしているため(In[64]の7行目、誤り訂正符号の実装意図とは逆に論理エラー率が増えたため)、d * 3回繰り返し時の損益分岐点を超える(損→益)程度に1回の繰り返しサイクルにおけるエラー率が小さな領域のみが描かれている。符号距離5と7の図において左下が白飛びしているのは、論理エラー率が8,192のシミュレーション回数では小さすぎて有効なデータが得られなかったためである。
だいたい予想通り p_meas と p_cnot のトレードオフ関係が示されている。測定のエラー率が小さな場合には2量子ビットゲート(CNOT)のエラー率は大きくても許され、また逆もしかりである。また符号距離が大きくなった場合、損益分岐点を超える領域が広くなることも注目に値する。
参考文献
[1] 6. Use pymatching to correct errors in a circuit GitHub
[2] CircuitRepeatBlock, GitHub
[3] 量子計算超入門, Web
[4] Keisuke Fuji, Quantum Computation with Topological Codes, From Qubit to Topological Fault-Tolerance, Springer, 2015
Discussion