Stim 使ってみる (量子) #2
検出器を使いこなしたい
基本動作
チュートリアル[1] では、誤り訂正符号の実装には検出器 DETECTOR を使うことをお奨めされる。測定値に関する引数が2つ取れるようで、測定結果間のパリティ(偶奇)が保存される様子。
検出器を使う理由を調べていると、検出器サンプルモードを使って反転したかどうかしないかをサンプルする方が計算コストが小さい[2]という記述を見つけた。DETECTORに関しては[3] を読むしかないと諦めて眺めていると、決定論的な測定によるエラー検出を定義するとのこと。
検出器にはお絵描きモードのために座標を打つことができるようだ。DETECTOR(座標X,座標Y) 測定値1 測定値2のように座標を設定できることに加え、SHIFT_COORDS 命令を使って全体の位置をずらしながら復号グラフをきれいに仕上げることができるようだ。チュートリアルの中では座標が使われているが、とりあえずお絵描きモードは無視して進める。
乱数発生器
In [1]: import stim
In [2]: import numpy, numpy as np
In [3]: circuit = stim.Circuit()
In [4]: circuit.append( 'H', [ 0 ])
In [5]: circuit.append( 'M', [ 0 ])
In [6]: circuit.append( 'H', [ 0 ])
In [7]: circuit.append( 'M', [ 0 ])
In [8]: circuit.diagram()
Out[9]: q0: -H-M:rec[0]-H-M:rec[1]-

アダマールを入れて乱数を作ってみる。それを2回繰り替えし毎度測定する。X状態(|+>)をZで測定するということで、XとZは反交換関係にあり決定論的な測定ではないが、検出器が動くのかどうかテストをしたいので2つの測定結果とそのXORによる検出器を構成してみる。rec[0]とrec[1]が測定結果に対応する。2回測定が終わった時点で検出器を構成する時点では rec[1] は最新の結果なので rec[-1]と指定できる。rec[0]は最新から一つ前の結果であるためrec[-2]に対応する。2回の測定結果の間の偶奇(パリティ)を用いて検出器を構成した。乱数を生成し動作を確認する。
In [10]: circuit.append( 'DETECTOR', [ stim.target_rec( -1 ), stim.target_rec( -2 )] )
In [11]: sampler = circuit.compile_detector_sampler()
In [12]: sampler.sample( shots = 8 )
Out[12]:
array([[ True], [False],
[False], [False],
[False], [False],
[ True], [False]])
Out[12]に示されるように、恐らく乱数が生成されているのであろう。1回目と2回目が同じ値が出る確率は0/0の場合と1/1の場合でそれぞれ 1/4であるはずなので、True の確率は1/2とならないといけないが Trueが少なめになっている。
In [13]: sampler = circuit.compile_detector_sampler()
In [14]: data = numpy.array( sampler.sample( shots = 2**10 ), dtype=int )
In [15]: numpy.sum( data ) / 2**10
Out[15]: np.float64(0.5126953125)
試行回数(shot)を1,024回に増やすと予想通り 50 % 程度となった。動作検証としては適切ではないが、とりあえず検出器は動いている。
何もしない回路
検出器からは少し離れて、何もせず緩和だけする回路で複数回観測を行ってみてはどうだろうか。分極解消チャネル(DEPOLARIZE1)を持つ緩和を10%だけ入れてひたすら観測を行う。
In [16]: circuit = stim.Circuit()
...: circuit.append( 'X', [ 0 ])
...: for i in range( 16 ):
...: circuit.append( 'DEPOLARIZE1', 0, 0.1 )
...: circuit.append( 'M', 0, 0.1 )
In [17]: circuit.diagram()
Out[17]: q0: -X-DEPOLARIZE1(0.1)-M(0.1):rec[0]-DEPOLARIZE1(0.1)-M(0.1):rec[1]-DEPOLARIZE1(0.1)-M(0.1):rec[2]-DEPOLARIZE1(0.1)-M(0.1):rec[3]-DEPOLARIZE1(0.1)-M(0.1):rec[4]-DEPOLARIZE1(0.1)-M(0.1):rec[5]-DEPOLARIZE1(0.1)-M(0.1):rec[6]-DEPOLARIZE1(0.1)-M(0.1):rec[7]-DEPOLARIZE1(0.1)-M(0.1):rec[8]-DEPOLARIZE1(0.1)-M(0.1):rec[9]-DEPOLARIZE1(0.1)-M(0.1):rec[10]-DEPOLARIZE1(0.1)-M(0.1):rec[11]-DEPOLARIZE1(0.1)-M(0.1):rec[12]-DEPOLARIZE1(0.1)-M(0.1):rec[13]-DEPOLARIZE1(0.1)-M(0.1):rec[14]-DEPOLARIZE1(0.1)-M(0.1):rec[15]-
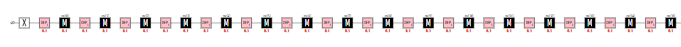
チュートリアルを読んでいるとテキスト表現だと繰り返し構文が使えるようだ。コード中に平文命令を入れるために stim.Circuit.append_from_stim_program_text()を用いた。こちらの方が記述がシンプルになる一方で、制御構造がPythonと平文で混ざるのは望ましくない。が、便利であることには代えられない。繰り返し回数も32回に増やした。
In [18]: circuit = stim.Circuit()
...: circuit.append( 'X', [ 0 ])
...: circuit.append_from_stim_program_text( '''
...: REPEAT 32 {
...: DEPOLARIZE1(0.1) 0
...: M 0
...: }
...: ''')
In [18]: circuit.diagram()
Out[18]:
/REP 32 \
q0: -X-|-------DEPOLARIZE1(0.1)-M:rec[0+iter]-|-
\ /
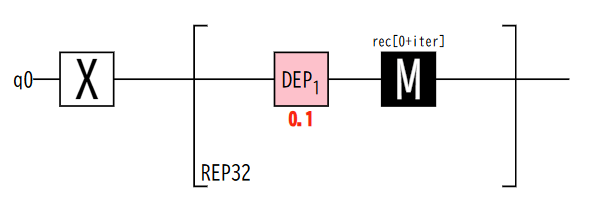
この回路をシミュレートし測定結果をサンプリングしてみる。試行回数を1回に設定し、回路内で32回の測定が行われる。結果はOut[20]の通りで、最初は1が観測されており、途中でビット反転が入り0の観測値が続き、最後の方でもう一度ビット反転が生じる様子が分かり、分極解消雑音により緩和が生じていることが分かる。
In [19]: data = numpy.array( sampler.sample( shots = 1 ), dtype=int )
In [20]: data
Out[20]:
array([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 1, 1, 1, 1, 1, 1]])
試行回数を128回まで増やしてみよう。下図は横軸に回路内の測定インデックス(時間軸)を、縦軸試行インデックスを示し(0 ~ 128回)、色により測定値( 0 or 1=黄色)を示している。測定インデックス(時間)が0に近い左端ではほとんどが回路中の最初のXビット反転により1が観測されているが、時間が経つにつれ図中右側ではランダムにビット反転する様子がわかる。
In [21]: data = numpy.array( sampler.sample( shots = 128 ), dtype=int )
In [22]: import matplotlib.pylab as pl
In [23]: pl.pcolor(data)
In [24]: pl.xlabel( 'Measurement index in the circuit' )
In [25]: pl.ylabel( 'Sample index' )
In [26]: pl.savefig( '1.svg')

この様子を試行回数方向に積算してみる。試行回数で割ることで1が得られた確率として表示すると、時間的に指数減衰していることが分かる。試行回数を十分に大きくとると分かりやすい。
In [27]: data_decay = np.sum( data, axis = 0 ) / 128
In [28]: pl.plot( data_decay, label = 'sample = 128' )
In [29]: pl.xlabel( 'Measurement index in the circuit' )
In [30]: pl.ylabel( 'Probability of 1' )
In [31]: pl.ylim(0,1)
In [32]: pl.savefig( '1.svg')

何もしない回路+検出器
In [33]: circuit = stim.Circuit()
In [34]: circuit.append( 'X', [ 0 ])
...: circuit.append( 'TICK' )
In [35]: circuit.append( 'M', [ 0 ])
...: circuit.append( 'DETECTOR', [stim.target_rec( -1 )] )
...: circuit.append( 'TICK' )
In [36]: circuit.append_from_stim_program_text( '''
...: REPEAT 32 {
...: DEPOLARIZE1(0.1) 0
...: M 0
...: DETECTOR rec[-1] rec[-2]
...: TICK
...: }
...: ''')
In [37]: circuit.diagram()
Out[37]:
/-------------------------\ /REP 64 /-----------------------------------------------------------------------\ \
q0: -X-M:rec[0]-DETECTOR:D0=rec[0]-|-------DEPOLARIZE1(0.3)-M:rec[1+iter]-DETECTOR:D[1+iter]=rec[1+iter]*rec[0+iter]-|-
\-------------------------/ \ \-----------------------------------------------------------------------/ /
この回路は、繰り返し中のアイドル(空き)時間に緩和が起きたものを理想的な測定器で測ったものとして解釈することもできるし、理想的なアイドルに対して雑音のある測定が繰り返されたものとして理解することもできる。

timeslice-svgという出力法があり、これを使うとやっと TICKの意味がよく分かった。TICK毎に操作が表示されることにより、時間的または空間的にどのような回路が印加されているのかを示すことができる。今回の例だと、1つの TICKの間に緩和と測定が繰り返されている。
In [38]: circuit.diagram('timeslice-svg')

この回路を8回だけサンプルすると下図のように測定の誤りが抽出される。チュートリアル [1] では測定とリセット MR が用いられているが、今回は単純な測定 M をIn[36]の繰り返し部分にて用いたため、エラーは単純にエラーの箇所のみを示しており、エラーシンドロームが生成されてはいない。
In [39]: sampler = circuit.compile_detector_sampler()
In [40]: data = numpy.array( sampler.sample( shots = 16 ), dtype = int )
In [41]: pl.figure( figsize = ( 10, 4 ))
...: pl.pcolor( data )
...: pl.xlabel( 'Detector index in the circuit' )
...: pl.ylabel( 'Sample index' )
...: pl.savefig( '1.svg' )
横軸が時間ごとに得られる検出器の結果とし、回路全体をサンプルした様子を縦軸に表示する。黄色が連続する部分は測定誤りが2連続で起きていることを意味し、測定エラーが10%程度でも場所によっては3回連続でエラーが生じている部分もあるので興味深い。

(古典)誤り検出符号
チュートリアルから少し離れてビット誤り訂正符号[4] の例をやってみる。符号距離が大きいと考えるのが大変なので、3ビットの検出符号を取り扱う。
この例ではQ0 Q1 Q2のうちQ0Q2 = 00 or 11を(量子ではない古典の)論理ビットだとみなし、そのパリティをQ1で測定することによりエラーを排除する。Q0Q2をデータビット、Q1をアンシラビットとする。Q0Q2=01 or 10はデータビットが1つだけビット反転した状態であり、Q1を用いてパリティを測定するとエラーがあったかどうか調べることができる。パリティの測定は Q0とQ2を直接測ることをせず(古典だけど今後のために量子っぽく取り扱おう)、Q1使って間接的に測定する。
In [42]: p_meas = 0.02
...: p_init = 0.10
In [43]: circuit = stim.Circuit()
In [44]: circuit.append( 'R', [ 0, 1, 2 ] )
...: circuit.append( 'DEPOLARIZE1', [ 0, 1, 2 ], p_init )
...: circuit.append( 'TICK' )
In [45]: circuit.append( 'CNOT', [ 0, 1 ])
...: circuit.append( 'CNOT', [ 2, 1 ])
...: circuit.append( 'TICK' )
In [46]: circuit.append( 'DEPOLARIZE1', [ 0, 1, 2 ], p_meas )
...: circuit.append( 'MR', [ 1 ])
...: circuit.append( 'DETECTOR', [stim.target_rec( -1 )] )
...: circuit.append( 'TICK' )
In [47]: circuit.append_from_stim_program_text( '''
...: REPEAT 32 {{
...: CNOT 0 1
...: CNOT 2 1
...: TICK
...: DEPOLARIZE1( {} ) 0 1 2
...: MR 1
...: DETECTOR rec[-1] rec[-2]
...: TICK
...: }}
...: '''.format( p_meas ))
In [48]: circuit.append( 'MR', [ 0, 2 ])
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -1 )], 0 )
In [49]: circuit.diagram()
Out[49]:
/----------------\ /-\ /--------------------------------------------\ /REP 32 /-\ /-------------------------------------------------------------------------\ \ /---------------------------------------\
q0: -R-DEPOLARIZE1(0.1)-@---DEPOLARIZE1(0.02)------------------------------|-------@---DEPOLARIZE1(0.02)-----------------------------------------------------------|-MR:rec[33]--------------------------------
| | | |
q1: -R-DEPOLARIZE1(0.1)-X-X-DEPOLARIZE1(0.02)-MR:rec[0]-DETECTOR:D0=rec[0]-|-------X-X-DEPOLARIZE1(0.02)-MR:rec[1+iter]-DETECTOR:D[1+iter]=rec[1+iter]*rec[0+iter]-|-------------------------------------------
| | | |
q2: -R-DEPOLARIZE1(0.1)---@-DEPOLARIZE1(0.02)------------------------------|---------@-DEPOLARIZE1(0.02)-----------------------------------------------------------|-MR:rec[34]-OBSERVABLE_INCLUDE:L0*=rec[34]-
\----------------/ \-/ \--------------------------------------------/ \ \-/ \-------------------------------------------------------------------------/ / \---------------------------------------/
In[44]からIn[46]が初期化の部分であり、緩和などのエラーがなければ Q0Q1Q2=000の状態を000にしたままなので、論理ビットがQ0Q2=00の場合にはあまり必要性を感じないが、例題に従うことにする。
In[47]の繰り返し部分が、Q0とQ2のエラーをQ1に取り込んで検出しているところになる。現実的にリセット無し測定 M を測定に使いたいところだが、とりあえずチュートリアルに合わせて測定後リセットする MR を採用する。2量子ビットゲートのエラーは考えず、In[44]の初期化のエラー、測定時のエラーを考慮する。測定時は非測定量子ビットも待機中なので、同じエラーレートで緩和することにした。
In[48]では最後に論理ビット状態を測定して確認するために、測定を行った。本来はこの測定は繰り返しのカッコ部分の最後の測定と同時に行われるはずなので、ここに測定の緩和は入れない。OBSERVABLE_INCLUDEという命令を使って、検出器サンプリングモードでも論理ビット状態(Q0とQ2の00と11を判別するためにQ2の測定値を)を追加した。

circuit.diagram('timeslice-svg')が便利であり、TICKごとに回路を空間的に表現してくれる。ここでは繰り返し数を1で表示している。Tick 0が初期化のエラーを導入し、Tick1~2で初期化の準備をして(チュートリアルに従う)、Tick 3~4 を何度も繰り返してエラーを検出する。Tick4に入っているQ0とQ2の緩和がデータ量子ビットの主な緩和源であり、Q1に入っている緩和が測定エラーの主な緩和源となる。

測定モードによるシミュレーション
測定モードを用いて回路をシミュレートし、結果を16回サンプリングする。測定結果を下図に示す。測定インデックスの0番目は、繰り返しの測定に入る前の測定に対応する。測定インデックス1~32が繰り返し中の測定結果、測定インデックス33と34が、最後のデータビット測定値となる。
In [50]: sampler = circuit.compile_sampler()
In [51]: data = numpy.array( sampler.sample( shots = 16 ), dtype = int )
In [52]: pl.pcolor( data )
In [53]: pl.xlabel( 'Measurement index in the circuit' )
In [54]: pl.ylabel( 'Sample index' )
In [55]: pl.savefig( '1.svg' )

- 試行 (Sample) インデックス1,2,3ではエラーが検出されていない。
- 試行インデックス4では、測定のエラーが単発的に生じている様子が分かる。
- 試行インデックス7では測定インデックス12からデータ量子ビットにエラーが生じた様子が観測され、測定インデックス33,34番のデータビット測定結果Q0 Q1=10からQ0が反転していることがわかる。
- 試行インデックス11では、測定インデックス1と15にてデータ量子ビットにエラーが生じている。2回エラーが生じるとQ0のエラー検出パリティは0に戻る。最後のデータ量子ビットの測定値がQ0 Q2=11であることから、初期状態00から11の論理ビット反転が生じたことが分かる。
検出器モードでサンプリング
検出器モードを用いて回路をシミュレートし結果をサンプリングする。測定値の最後に追加したQ2の値は 'OBSERVABLE'として得られ、サンプラーにseparate_observables = Trueと設定して取得する必要があった(まとめられるのかと思っていた)。検出器のデータの末尾に追加して表示する。
In [56]: sampler = circuit.compile_detector_sampler()
In [57]: derr, obs = sampler.sample( shots = 16, separate_observables = True )
...: data = numpy.array( np.hstack(( derr, obs )), dtype = int )
In [58]: pl.clf()
...: pl.pcolor( data )
...: pl.xlabel( 'Measurement index in the circuit' )
...: pl.ylabel( 'Sample index' )
...: pl.savefig( '1.svg' )

測定エラーは典型的に時間方向に2連続の1、データ量子ビットのエラーは1点の1として表示される。
終端処理
初期化のエラーとパリティ測定用の量子ビットQ1のエラーを無しにして、しばらくデータを眺めていると奇妙なデータが見られた。下がデータ量子ビットQ0, Q2にのみエラーが生じる回路である。
In [59]: p_meas = 0.02
...: circuit = stim.Circuit()
...: circuit.append( 'R', [ 0, 1, 2 ] )
...: circuit.append( 'TICK' )
...: circuit.append( 'CNOT', [ 0, 1 ])
...: circuit.append( 'CNOT', [ 2, 1 ])
...: circuit.append( 'TICK' )
...: circuit.append( 'MR', [ 1 ])
...: circuit.append( 'DETECTOR', [stim.target_rec( -1 )] )
...: circuit.append( 'TICK' )
...: circuit.append_from_stim_program_text( '''
...: REPEAT 32 {{
...: CNOT 0 1
...: CNOT 2 1
...: TICK
...: DEPOLARIZE1( {} ) 0 2
...: MR 1
...: DETECTOR rec[-1] rec[-2]
...: TICK
...: }}
...: '''.format( p_meas ))
...: circuit.append( 'MR', [ 0, 2 ])
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -1 ) ], 0 )
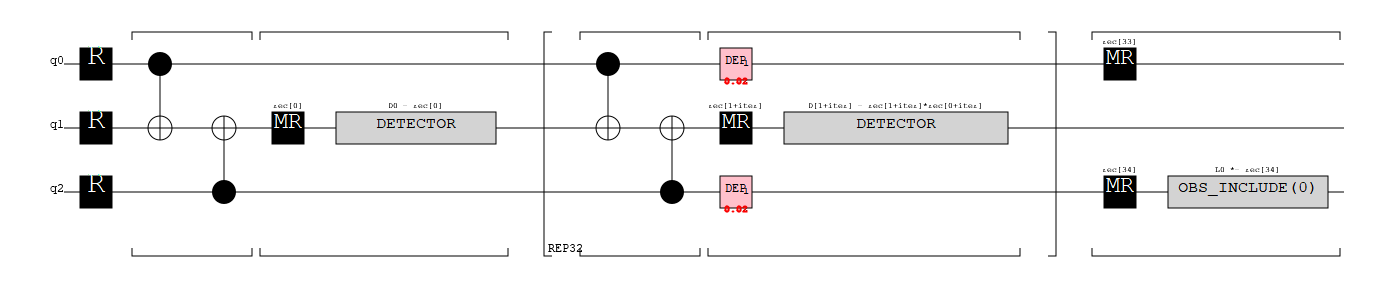
測定モードで回路をシミュレーションした場合、データ量子ビットが反転するとアンシラ量子ビットQ1が黄色の長い横線となり1が続く。2回反転した場合にはアンシラ量子ビットQ1がゼロとなる。奇妙な場合とは、データ量子ビットが奇数回反転しているのに、データ量子ビットのパリティQ0 Q2が偶になっていたり、アンシラ量子ビットQ1が偶数回反転しているのに、データ量子ビットQ0 Q2のパリティが奇になっている(本来はQ1で検出されないとならない)場合が見られた。
In [60]: sampler = circuit.compile_sampler()
...: derr = sampler.sample( shots = 1024 )
...: data = numpy.array( derr, dtype = int )
In [61]: vault = []
...: for _single in data:
...: m0 = _single[1:-2]
...: m1 = _single[:-3]
...: odd_detflip = numpy.sum( m0 ^ m1 ) % 2
...: odd_dataflip = _single[-2] ^ _single[-1]
...: if 1 == odd_detflip ^ odd_dataflip:
...: vault.append( _single )
...: data = numpy.array( vault )
In [62]: pl.clf()
...: pl.figure( figsize = ( 8, 4 ))
...: pl.pcolor( data )
...: pl.xlabel( 'Measurement index in the circuit' )
...: pl.ylabel( 'Sample index' )
...: pl.savefig( '1.svg' )
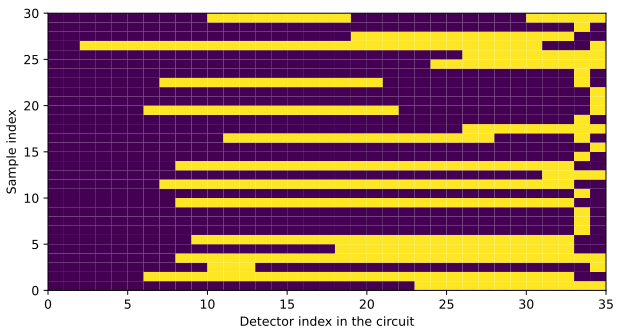
何度かサンプリングしてそのような場合のみを下図に抽出した(図作成上のミスで横軸がDetector indexとなっているがMeasurement indexである)。ここで測定インデックス0は繰り返しループ直前の測定、1~32が繰り返し中の測定値、33,34がQ0とQ2のデータである。例えば
- 試行インデックス1は測定インデックス6でデータ量子ビットのエラーが生じているにも関わらず、33、34番の測定インデックスに示されるQ0 Q2の測定値エラーが生じていない。
- 試行インデックス10はデータ量子ビットのエラーが検出されていないにも関わらず、測定インデックス33,34番においてQ0の値が反転している。
可能性としては32番目の測定が終わった後から33、34を測定する前までにエラーが生じた場合、つまり33、34番目に示されるデータ量子ビットの測定エラーにより生じていると考えられる。1024回試行して30回程度が抽出されているのでエラー率は3%、ちょうどデータ量子ビットの測定エラー由来(2%+2%)*(2/3)程度と考えて良いだろう。
ここでチュートリアルをよく見ると、繰り返しの最後に検出器が追加されていることに気づいた(ことにしよう)。終端処理だ。
In [63]: p_meas = 0.02
...: circuit = stim.Circuit()
...: circuit.append( 'R', [ 0, 1, 2 ] )
...: circuit.append( 'TICK' )
...: circuit.append( 'CNOT', [ 0, 1 ])
...: circuit.append( 'CNOT', [ 2, 1 ])
...: circuit.append( 'TICK' )
...: circuit.append( 'MR', [ 1 ])
...: circuit.append( 'DETECTOR', [stim.target_rec( -1 )] )
...: circuit.append( 'TICK' )
...: circuit.append_from_stim_program_text( '''
...: REPEAT 32 {{
...: CNOT 0 1
...: CNOT 2 1
...: TICK
...: DEPOLARIZE1( {} ) 0 2
...: MR 1
...: DETECTOR rec[-1] rec[-2]
...: TICK
...: }}
...: '''.format( p_meas ))
In [64]: circuit.diagram()
Out[64]:
/-\ /--------------------------\ /REP 32 /-\ /----------------------------------------------------------\ \
q0: -R-@--------------------------------|-------@---DEPOLARIZE1(0.02)--------------------------------------------|-
| | | |
q1: -R-X-X-MR:rec[0]-DETECTOR:D0=rec[0]-|-------X-X-MR:rec[1+iter]----DETECTOR:D[1+iter]=rec[1+iter]*rec[0+iter]-|-
| | | |
q2: -R---@------------------------------|---------@-DEPOLARIZE1(0.02)--------------------------------------------|-
\-/ \--------------------------/ \ \-/ \----------------------------------------------------------/ /
In [65]: circuit.append( 'MR', [ 0, 2 ])
In [66]: circuit.append('DETECTOR', [stim.target_rec( -3 ),
...: stim.target_rec( -1 ),
...: stim.target_rec( -2 ) ] )
In [67]: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -1 ) ], 0 )
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -2 ) ], 1 )
In [68]: circuit.diagram()
Out[68]:
/-\ /--------------------------\ /REP 32 /-\ /----------------------------------------------------------\ \ /----------------------------------------------------------------------------\
q0: -R-@--------------------------------|-------@---DEPOLARIZE1(0.02)--------------------------------------------|-MR:rec[33]--OBSERVABLE_INCLUDE:L1*=rec[33]-------------------------------------
| | | |
q1: -R-X-X-MR:rec[0]-DETECTOR:D0=rec[0]-|-------X-X-MR:rec[1+iter]----DETECTOR:D[1+iter]=rec[1+iter]*rec[0+iter]-|-------------DETECTOR:D33=rec[32]*rec[34]*rec[33]-------------------------------
| | | |
q2: -R---@------------------------------|---------@-DEPOLARIZE1(0.02)--------------------------------------------|-MR:rec[34]--OBSERVABLE_INCLUDE:L0*=rec[34]-------------------------------------
\-/ \--------------------------/ \ \-/ \----------------------------------------------------------/ / \----------------------------------------------------------------------------/
In[66]で追加されている検出器は、Out[68]にの末尾に見られるようにQ0 (rec[33]), Q2(rec[34]) の測定値の積を用いて、あたかもCNOTによりパリティを集めてきたかのようにQ0,Q2のパリティを作っている。測定エラーのシンドロームは検出器における直前の測定値と現在の測定値のパリティ(XOR)を計算する。Q0 (rec[33]), Q2(rec[34])の測定値の積によるパリティに対して直前の測定データ(rec[32], iter=31)とのパリティを計算し、シンドロームを生成している。この検出器追加により最後のデータ量子ビットの測定エラー(または完璧な測定の前に生じたエラー)を検出することができる。
今回の回路では最後に測定するデータ量子ビット Q0 Q2 の値を全て確認できるように OBSERVABLE_INCLUDE をQ0、Q2に追加した。
In [69]: sampler = circuit.compile_detector_sampler()
...: derr, obs = sampler.sample( shots = 16*1024, separate_observables = True )
In [70]: numpy.sum(derr,axis=1) + numpy.sum(obs,axis=1)
Out[70]: array([0, 0, 0, 2, 0, 0, 0, 0, 2, 4, 2, 2, 4, 4, 4, 2])
In [71]: ( numpy.sum( derr, axis = 1 )
...: + numpy.sum( obs, axis = 1 )) % 2
Out[71]: array([0, 0, 0, ..., 0, 0, 0])
In [72]: sum(( numpy.sum( derr, axis = 1 ) + numpy.sum( obs, axis = 1 )) % 2 )
Out[72]: np.int64(0)
検出器モードで回路をシミュレートし、エラーシンドロームをサンプリングする。検出器によりビット反転が観測された回数と、Q0 Q1の1の数を足すと必ず偶数であることが確認された(Out[70])。この数のmod2を取ると全てゼロであり (Out[71])、16k回の試行回数すべてにおいて足し上げるとゼロとなることが確認された。終端処理によりデータ量子ビットのシンドロームがきちんと計算できていることが分かった。
(古典)誤り訂正符号
先ほどの例は検出だけだったため、1ビットの誤りが訂正できる反復符号を取り扱う。5量子ビット Q4Q3Q2Q1Q0 のうち、Q4とQ2とQ0がデータ量子ビットであり、Q3はQ4とQ2のパリティを間接的に測定するための量子ビット(アンシラ量子ビット)、Q1はQ2とQ0のパリティを間接的に測定するアンシラ量子ビットとする。回路は先ほどと同じように、00000の状態から始めてみる。下が距離3の反復符号である。
q0: -R-@-R---@-------------
| |
q1: -R-X-X-R-X-X-MR:rec[0]-
| |
q2: -R-@-@-R-@-@-----------
| |
q3: -R-X-X-R-X-X-MR:rec[1]-
| |
q4: -R---@-R---@-----------
エラーが無い場合、下のように実装される。CNOT 0 1 2 3は CNOT 0 1 CNOT 2 3と同じ意味であり、一度に2対の量子ビットにCNOTを印加することができる。検出器は先と同じように前の測定結果とのXORをとり (In[76]の8行目) シンドロームを生成する。繰り返し後にデータ量子ビット Q0, Q2, Q4を測定し、前述の通りシンドロームの終端処理を行う (In[78])。
In [73]: circuit = stim.Circuit()
...: circuit.append( 'R', [ 0, 1, 2, 3, 4 ] )
...: circuit.append( 'TICK' )
In [74]: circuit.append( 'CNOT', [ 0, 1, 2, 3 ])
...: circuit.append( 'TICK' )
...: circuit.append( 'CNOT', [ 2, 1, 4, 3 ])
...: circuit.append( 'TICK' )
In [75]: circuit.append( 'MR', [ 1, 3 ])
...: circuit.append( 'DETECTOR', [stim.target_rec( -2 )] )
...: circuit.append( 'DETECTOR', [stim.target_rec( -1 )] )
...: circuit.append( 'TICK' )
In [76]: circuit.append_from_stim_program_text( '''
...: REPEAT 32 {{
...: CNOT 0 1 2 3
...: TICK
...: CNOT 2 1 4 3
...: TICK
...: MR 1 3
...: DETECTOR rec[-4] rec[-2]
...: DETECTOR rec[-3] rec[-1]
...: TICK
...: }}
...: '''
In [77]: circuit.append( 'MR', [ 0, 2, 4 ]) # -1 Q4, -2 Q2, -3 Q0, -4 Q3, -5 Q1
In [78]: circuit.append('DETECTOR', [stim.target_rec( -5 ),
...: stim.target_rec( -3 ),
...: stim.target_rec( -2 ) ] )
...: circuit.append('DETECTOR', [stim.target_rec( -4 ),
...: stim.target_rec( -2 ),
...: stim.target_rec( -1 ) ] )
In [79]: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -3 ) ], 0 )
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -2 ) ], 1 )
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -1 ) ], 2 )
In [80]: circuit.diagram()
Out[80]:
/--------------------------\ /REP 32 /---------------------------------------------------------------\ \ /----------------------------------------------------------------------------\
q0: -R-@--------------------------------|-------@---------------------------------------------------------------------|-MR:rec[66]--------------------------------------OBSERVABLE_INCLUDE:L0*=rec[66]-
| | | |
q1: -R-X-X-MR:rec[0]-DETECTOR:D0=rec[0]-|-------X-X-MR:rec[2+iter*2]-DETECTOR:D[2+iter*2]=rec[0+iter*2]*rec[2+iter*2]-|------------DETECTOR:D66=rec[64]*rec[66]*rec[67]--------------------------------
| | | |
q2: -R-@-@------------------------------|-------@-@-------------------------------------------------------------------|-MR:rec[67]--------------------------------------OBSERVABLE_INCLUDE:L1*=rec[67]-
| | | |
q3: -R-X-X-MR:rec[1]-DETECTOR:D1=rec[1]-|-------X-X-MR:rec[3+iter*2]-DETECTOR:D[3+iter*2]=rec[1+iter*2]*rec[3+iter*2]-|------------DETECTOR:D67=rec[65]*rec[67]*rec[68]--------------------------------
| | | |
q4: -R---@------------------------------|---------@-------------------------------------------------------------------|-MR:rec[68]--------------------------------------OBSERVABLE_INCLUDE:L2*=rec[68]-
\--------------------------/ \ \---------------------------------------------------------------/ / \----------------------------------------------------------------------------/
当たり前だが、緩和源が入っていないため、サンプルしても0が返ってきて面白くない。
復号グラフ
エラー源を初期化エラー、読み出しエラーとその待ち時間に入れて、復号グラフを作ってみる。回路は下の通り。復号グラフを生成しようとしたところ、きちんと検出器の座標が与えられていなかったため、ぐちゃぐちゃのグラフが生成されてしまった。circuit.append( 'DETECTOR', [stim.target_rec( -2 )], [ X座標, Y座標] ) のように、DETECTOR命令に座標を与えることができる。また、ループ分の中では、SHIFT_COORDS(0, 1)のように全体の座標を移動させることができる。終端処理の検出器はシフト命令を使わずに ( 1, 1) のように手入力をした。
In [81]: p_meas = 0.02
...: p_init = 0.10
...: p_cnot = 0.05
...: circuit = stim.Circuit()
...: circuit.append( 'R', [ 0, 1, 2, 3, 4 ] )
...: circuit.append( 'DEPOLARIZE1', [ 0, 1, 2, 3, 4 ], p_init )
...: circuit.append( 'TICK' )
...: circuit.append( 'CNOT', [ 0, 1, 2, 3 ])
...: circuit.append( 'TICK' )
...: circuit.append( 'CNOT', [ 2, 1, 4, 3 ])
...: circuit.append( 'TICK' )
...: circuit.append( 'DEPOLARIZE1', [ 0, 1, 2, 3, 4 ], p_meas )
...: circuit.append( 'MR', [ 1, 3 ])
...: circuit.append( 'DETECTOR', [stim.target_rec( -2 )], [ 1, 0] )
...: circuit.append( 'DETECTOR', [stim.target_rec( -1 )], [ 3, 0] )
...: circuit.append( 'TICK' )
...: circuit.append_from_stim_program_text( '''
...: REPEAT 31 {{
...: CNOT 0 1 2 3
...: TICK
...: CNOT 2 1 4 3
...: TICK
...: DEPOLARIZE1( {} ) 0 1 2 3 4
...: MR 1 3
...: SHIFT_COORDS(0, 1)
...: DETECTOR(1,0) rec[-4] rec[-2]
...: DETECTOR(3,0) rec[-3] rec[-1]
...: TICK
...: }}
...: '''.format( p_meas ))
...: circuit.append( 'MR', [ 0, 2, 4 ])
...: circuit.append('DETECTOR', [stim.target_rec( -5 ),
...: stim.target_rec( -3 ),
...: stim.target_rec( -2 ) ], [ 1, 1 ] )
...: circuit.append('DETECTOR', [stim.target_rec( -4 ),
...: stim.target_rec( -2 ),
...: stim.target_rec( -1 ) ], [ 3, 1 ] )
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -3 ) ], 0 )
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -2 ) ], 1 )
...: circuit.append('OBSERVABLE_INCLUDE', [ stim.target_rec( -1 ) ], 2 )
In [82]: circuit.diagram('timeline-svg')

復号グラフを表示するためには, circuit.detector_error_model()によりエラーモデルを生成し、diagram("matchgraph-svg")にてsvgファイルを生成する。グラフが大きくなりすぎないように、ループの回数を3回とした。
In [83]: dem = circuit.detector_error_model()
In [84]: dem
Out[84]:
stim.DetectorErrorModel('''
error(0.0666667) D0 D1 L1
error(0.0782222) D0 D2
error(0.0666667) D0 L0
error(0.0782222) D1 D3
error(0.0666667) D1 L2
error(0.0133333) D2 D3 L1
error(0.0133333) D2 L0
error(0.0133333) D3 L2
detector(1, 0) D0
detector(3, 0) D1
repeat 2 {
error(0.0133333) D2 D4
error(0.0133333) D3 D5
error(0.0133333) D4 D5 L1
error(0.0133333) D4 L0
error(0.0133333) D5 L2
shift_detectors(0, 1) 0
detector(1, 0) D2
detector(3, 0) D3
shift_detectors 2
}
error(0.0133333) D2 D4
error(0.0133333) D3 D5
error(0.0133333) D4 D5 L1
error(0.0133333) D4 L0
error(0.0133333) D5 L2
shift_detectors(0, 1) 0
detector(1, 0) D2
detector(3, 0) D3
detector(1, 1) D4
detector(3, 1) D5
''')
''')
In [85]: dem.diagram("matchgraph-svg")
Out[85]:
下の図は得られた復号グラフにエラー率、検出器番号を記入している。検出器の番号は、Out[84]中のshift_detectors 増分によって番号がどんどん大きくなることに注意されたい。

6.6%のエラー率は初期化エラー率の2/3に対応する。分極解消雑音チャネルを採用しており、p/3
の確率で生じるX軸ビット反転と同じくp/3で生じるY軸ビット反転により2p/3で初期化のエラーが生じることになる。初期化のエラーとしてY軸ビット反転が生じるのは不適切な気がするので、エラーモデルとしてX_ERRORを採用したほうがよかったかもしれない。
- D0とD1をつなぐ辺はQ2の初期化エラーが検出される確率 6.6 %が割りあてられている。Q2の初期化エラーが生じると、下図青線のようにD0とD1の検出器でシンドロームが生成される。D0とD1が同時に1となる場合(ホットシンドローム)、Q2のエラーである確率が高いと設定される。
- D0とL0をつなぐ辺は、Q0の初期化エラーが検出される確率 6.6% が割り当てられている(下図赤線)。ここでL0やL2は符号の境界に対応し、Q0でエラーが生じた場合にはD0で検出され、D0のホットシンドロームとL0とがマッチングされる。
- D0-D2をつなぐ辺は、Q1の初期化のエラー 6.6% が、Q1観測前のエラー 1.3% ( 2 % の分極解消エラーに 2p/3 が寄与する) が足されて読み出し誤りとして検出される(下図黒線)。読み出し誤りが生じた場合、時間方向に対になるようにシンドロームが出力され、その二つのマッチングをとることで誤りが訂正される。

誤り訂正
In [86]: sampler = circuit.compile_detector_sampler()
In [87]: derr, obs = sampler.sample( shots = 1, separate_observables = True )
In [88]: numpy.array( derr[0], dtype=int).reshape((33,2)).T
Out[88]:
array([[1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[1,1,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0]])
# D D D D D D D D D D D D D D D D D D D
# 0 2 4 6 8 10 14 18 22 26 30 34 38 42 46 50 54 58 62
# 1 3 5 7 9 11 15 19 23 27 31 35 39 43 47 51 55 59 63
エラーシンドロームをサンプルしてみよう。Q1とQ3で検出されたエラーシンドロームが、D0,D1,...と並び、Out[88]の上側がQ1で測定されるエラーシンドロームD0,D2,D4...、下側がQ3で検出されるエラーシンドロームD1,D3,D5..である。
頭の中で復号してみる。
- 最初のD0=D1=1はQ2のエラーとし、D0-D1がマッチングする。
- 次のD3=1はQ4がエラーを生じた場合として、D3-L2がマッチングする。
- D22=D23=1はQ2のエラーとしてD22-D23がマッチングする
- D36=1はQ0のエラーとしてD36-L0がマッチングする
- D43=D45=1は測定のエラーとして、時間方向にマッチングする
これを集計すると、Q2のエラーは2回生じているため元通り、Q0は1回、Q4は1回なので、Q4とQ1を反転させればよいはずである。データ量子ビットの測定値は下記の通りで、エラー訂正操作を加えると Q0 Q2 Q4=111となり、論理エラーを生じてしまった。
In [89]: numpy.array(obs,dtype=int)
Out[89]: array([[0, 1, 0]])
この反省をもとに再度頭の中で復号を行う。
- 最初のD0=D1=1はQ2のエラーとするより、D1=D3=1についてD1-D3の重みの方が大きい (7.8%)ことよりQ3の読み出しのエラーとする。
- ペアを失ってしまったD0=1はD0-L0=6%の辺でマッチングし、Q0のエラーとする。
- D22=D23=1はQ2のエラーとしてD22-D23がマッチングする
- D36=1はQ0のエラーとしてD36-L0がマッチングする
- D43=D45=1は測定のエラーとして、時間方向にマッチングする
これを集計するとQ0のエラーが2回で元通り、Q2のエラーが1回とすると、Q2の反転操作をQ0Q2Q4の測定値に加えると 000 ともともとの誤りが訂正されることになる。
これを pymatching [5]を用いて復号すると、デコーダに復号グラフのオブジェクトを直接追加することができる (In[92])。あとは推定値を教えて下さいとお願いすると、訂正するべき箇所を教えてもらえる。特に復号器の中身を知らなくでも簡単に復号することができた。
In [90]: import pymatching
In [91]: dem = circuit.detector_error_model()
In [92]: matcher = pymatching.Matching.from_detector_error_model( dem )
In [93]: predictions = matcher.decode_batch( derr )
In [94]: predictions
Out[94]: array([[0, 1, 0]], dtype=uint8)
参考文献
[1] 4. Add detector annotations to a circuit, and sample them, gitHub
[2] How does Stim's detector sampler work?, StackExchange
[3] DETECTOR, GitHub
[4] Repetition Code Circuit, gitHub
[5] PyMatching 2, readthedocs
Discussion