💬

Stim 使ってみる (量子)

2024/10/05に公開

Stimlib

クリフォード回路のシミュレータとして面白そうなライブラリ Stim [1]があるとのことで使ってみることに。何ができるかREADMEを読んでみたところ、いろいろできる様子。論文[2]を読んでみる元気はないため、とりあえず使ってみてから考えることにする。

クリフォード回路の速いシミュレータ
半自動の復号器の構成
あとはいろいろ

クリフォードゲート

クリフォード群 [3]は難しいので、パウリ行列をパウリ行列へ移すことのできるゲートとして理解した。このようなゲートの変換に強いとQuantattack [4]のゲームで強くなる。パウリ行列 {I, X, Y, Z}を挟んだ時に別のパウリ行列へ変換される。1量子ビットパウリ行列の変換の例としては下の通り。

H Z H = X
H X H = Z
S X S = Y

量子回路はクリフォードゲートだと量子コンピュータの強さは損なわれてしまうが、これさえ使えればしばらくは大丈夫な人が多いのでそれに従うことにした。

インストール

Windows10のpipenv環境ではこれで動きました。

python -m pipenv install stim

In [1]: import stim
In [2]: print(stim.__version__)
1.14.0

ベル状態生成まで

こちらLinkのチュートリアルを進めてみよう。

回路にアダマールを量子ビット0にかけて、0->1に対してCNOTしてベル対を作る例題。circuitと入力すると stim の中間表現が出力され、circuit.diagram() で量子回路表現が出力される。

In [3]: circuit = stim.Circuit()
In [4]: circuit.append('H',[0])
In [5]: circuit.append('CNOT',[0,1])
In [6]: circuit
Out[6]:
stim.Circuit('''
    H 0
    CX 0 1
''')
In [7]: circuit.diagram()
Out[7]:
q0: -H-@-
       |
q1: ---X-

SVGベクタ画像形式でも出力ができる様子。回路が大きくなった場合には、こういうのが助かる。ipython上から実行していると、画像ではなくsvgファイルの中身が表示されてしまった。ファイルに保存すると見られるようになる。

In [8]: circuit.diagram('timeline-svg')
Out[8]:
<svg viewBox="0 0 224 224"  version="1.1" xmlns="http://www.w3.org/2000/svg">
<g id="qubit_lines">
<path id="qubit_line:0" d="M64,64 L192,64 " stroke="black"/>
<text dominant-baseline="central" text-anchor="end" font-family="monospace" font-size="12" x="64" y="64">q0</text>
<path id="qubit_line:1" d="M64,128 L192,128 " stroke="black"/>
<text dominant-baseline="central" text-anchor="end" font-family="monospace" font-size="12" x="64" y="128">q1</text>
</g>
<rect x="80" y="48" width="32" height="32" stroke="black" fill="white"/>
<text dominant-baseline="central" text-anchor="middle" font-family="monospace" font-size="30" x="96" y="64">H</text>
<path d="M160,64 L160,128 " stroke="black"/>
<circle cx="160" cy="64" r="12" stroke="none" fill="black"/>
<circle cx="160" cy="128" r="12" stroke="black" fill="white"/>
<path d="M148,128 L172,128 M160,116 L160,140 " stroke="black"/>
</svg>

アダマールのHのサイズがちょっとカッコ悪いけど。

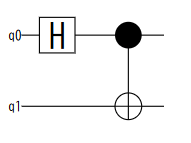
すっかり観測を忘れていた。観測をここで入れてみよう。

In [9]: circuit.append("M", [0,1])
In [10]: circuit.diagram()
Out[10]:
q0: -H-@-M:rec[0]-
       |
q1: ---X-M:rec[1]-

回路をコンパイルして結果をサンプルしてみる。結果が numpy.ndarrayのbooleanで出力される。どうせなら0,1で出力されてほしかった。ベル状態 |00>+|11>ができているため、二つの測定結果は相関しているはず。

In [11]: sampler = circuit.compile_sampler()
In [12]: sampler.sample(shots=16)
Out[12]:
array([[ True,  True],  [ True,  True],
       [False, False],  [False, False],
       [ True,  True],  [False, False],
       [False, False],  [False, False],
       [False, False],  [ True,  True],
       [False, False],  [ True,  True],
       [ True,  True],  [False, False],
       [False, False],  [ True,  True]])

ベル測定がZ測定で相関したからといって安心はできない。測定前にアダマールを足して、X測定でもきちんと相関しているかどうか確認したい。stim.Circuitにはinsert()という機能があるらしく、後ろからのインデックスに回路を追加することができる。当然だがX測定においても問題なくベル対 |00>+|11> = |++>+|-->は相関することが確認できる(結果非表示)。

In [13]: circuit_add = stim.Circuit()
In [14]: circuit_add.append('H',[0,1])
In [15]: circuit.insert(-1,circuit_add)
In [16]: circuit.diagram()
Out[16]:
q0: -H-@-H-M:rec[0]-
       |
q1: ---X-H-M:rec[1]-

追加できそうな操作

追加できそうなゲートを調べてみたところ、X, Y, Z はパウリ反転、CX, CY,CZは2量子ビットゲート、Hはアダマール, S はZ軸の90度回転として追加できる。もちろんクリフォードゲートのみなので、Tは当たり前だが追加できない。調べているとかなりたくさんのクリフォードゲートが使えるようだ[6]。

リセット回路

Rを用いるとリセットができる様子。何がなんでも状態を |0>にする射影演算子がかかるようなふるまいをしている。

In [17]: circuit = stim.Circuit()
    ...: circuit.append('H',[0])
    ...: circuit.append('CX',[0,1])
    ...: circuit.append('CX',[1,2])
    ...: circuit.append('R',[0])
    ...: circuit.append('M',[0,1,2])
    ...: circuit.diagram()
Out[17]:
q0: -H-@-R-M:rec[0]-
       |
q1: ---X-@-M:rec[1]-
         |
q2: -----X-M:rec[2]-
In [18]: sampler = circuit.compile_sampler()
    ...: sampler.sample(shots=8)
Out[18]:
array([[False, False, False], [False,  True,  True],
       [False, False, False], [False,  True,  True],
       [False, False, False], [False, False, False],
       [False,  True,  True], [False,  True,  True]])

TICKとは何か？

In[20],In[21]で記述したゲートが同じタイミングで配置されるように、stim は回路を詰め込んで配置してくれるようだ。これをずらして配置するバリアのようなものが TICK なのだと想像した。

In [19]: circuit = stim.Circuit()
In [20]: circuit.append('H',[0])
In [21]: circuit.append('Z',[1])
In [22]: circuit.append('CNOT',[0,1])
In [23]: circuit.diagram()
Out[23]:
q0: -H-@-
       |
q1: -Z-X-

ハの字型の区間を示す謎のコメントのようなものが回路の記述に入った。SVGファイルをみて、多分何か使い方が違うような気がする。後々どこかで分かるだろう。

In [24]: circuit = stim.Circuit()
In [25]: circuit.append('H',[0])
In [26]: circuit.append('TICK')
In [27]: circuit.append('Z',[1])
In [28]: circuit.append('CNOT',[0,1])
In [29]: circuit.diagram()
Out[29]:
       /-\
q0: -H---@-
         |
q1: ---Z-X-
       \-/

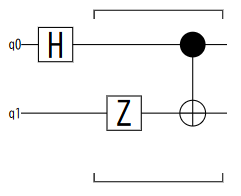
1量子ビット緩和源

DEPOLARIZE1 が緩和源のようだ。0番目の量子ビットに、10 % の緩和を設定してみる。量子ビット番号と、緩和の強さ p を 0.1 = 10 % のように設定する。結果は0.0666と約15分の1なので、緩和率を p = 10 % として、p/3のX軸パウリ反転とp/3のY軸パウリ反転で計2p/3の確率で初期状態 |0> を反転している。p/3の確率で生じるZ軸パウリ反転は |0>状態に影響はない。

In [30]: circuit = stim.Circuit()
In [31]: circuit.append( 'TICK' )
In [32]: circuit.append( 'DEPOLARIZE1', 0, 0.1 )
In [33]: circuit.append( 'M', [0] )
In [34]: circuit.diagram()
Out[34]:
       /-----------------------\
q0: ---DEPOLARIZE1(0.1)-M:rec[0]-
       \-----------------------/

In [35]: sampler = circuit.compile_sampler()
In [36]: p_e = float( numpy.sum( sampler.sample( shots = 1024 )) / 1024. )
Out[36]: 0.066623046875

T1緩和させてみる。使い方がいまいちわからないTICKを入れている。初期状態から緩和を何回かいれてその都度観測し、観測結果をリストに保存する。これで時間的に(ステップが増える毎に)緩和する様子が分かるはず。

In [37]: T1s = []
     ...: for i in range(32):
     ...:     circuit = stim.Circuit()
     ...:     for j in range(i):
     ...:         circuit.append( 'TICK' )
     ...:         circuit.append( 'DEPOLARIZE1', 0, 0.1 )
     ...:     circuit.append( 'M', [0] )
     ...:     sampler = circuit.compile_sampler()
     ...:     p_e = float( numpy.sum( sampler.sample( shots = 2**10 )) / 2**10 )
     ...:     T1s.append( p_e )
In [38]: T1s
Out[38]:
[0.0,           0.0634765625,  0.1240234375, 0.166015625,
 0.205078125,   0.240234375,   0.306640625,  0.349609375,
 0.3603515625,  0.3251953125,  0.4033203125, 0.4248046875,
 0.42578125,    0.4365234375,  0.458984375,  0.4296875,
 0.4404296875,  0.45703125,    0.4716796875, 0.462890625,
 0.4765625,     0.47265625,    0.48828125,   0.5068359375,
 0.4921875,     0.51171875,    0.5,          0.4716796875,
 0.51953125,    0.5185546875,  0.486328125,  0.4951171875]

In [39]: import matplotlib.pylab as pl
In [40]: pl.savefig( '1.svg')
In [41]: pl.plot( T1s )
In [42]: pl.ylim(0,1)
In [43]: pl.savefig( '1.svg')

Z軸を|1>状態観測確率とするとステップ毎に緩和する様子がシミュレートされていることが分かる。物理系に依るが初期状態を|0>を基底状態とすると、緩和により励起が増えるヒーティングが生じている様子がシミュレートされている。

横緩和もしらべてみる。初期状態にHを入れてX軸に状態を用意し、測定前にHを入れてX軸を測定する。

In [44]: T2s = []
     ...: for i in range(32):
     ...:     circuit = stim.Circuit()
     ...:     circuit.append( 'H', [0] )
     ...:     for j in range(i):
     ...:         circuit.append( 'TICK' )
     ...:         circuit.append( 'DEPOLARIZE1', 0, 0.1 )
     ...:     circuit.append( 'H', [0] )
     ...:     circuit.append( 'M', [0] )
     ...:     sampler = circuit.compile_sampler()
     ...:     p_x = float( numpy.sum( sampler.sample( shots = 2**10 )) / 2**10 )
     ...:     T2s.append( p_x )
In [45]: pl.plot( T2s )
In [46]: pl.savefig( '1.svg' )

T1の計算値にT2の計算値が上書きされるように緩和していることがわかる。ちょうどX~Zの3軸が対称的につぶれていく分極解消雑音 (depolarizing channel)の様子がシミュレートされている。

2量子ビット緩和源

2量子ビット緩和源 DEPOLARIZE2 という操作もあるようである。主にCNOTの後にいれて2量子ビットゲートの緩和をシミュレートするようである。量子ビット番号を[0,1]のように指定して、緩和の強さを 0.1 = 10 % のように指定する。2量子ビット分極消去緩和源の雰囲気を調べるために、1量子ビットの緩和源と2量子ビットの緩和源を比べてみる。

1量子ビット緩和と2量子ビット緩和のステップごとのT1を測定してみる。下図(上)では1量子ビット緩和を2量子ビットゲートに印加したもの、下図(下)では2量子ビット緩和源を印加したもの。2量子ビット緩和源では、DEP2というつながった箱が表示された。

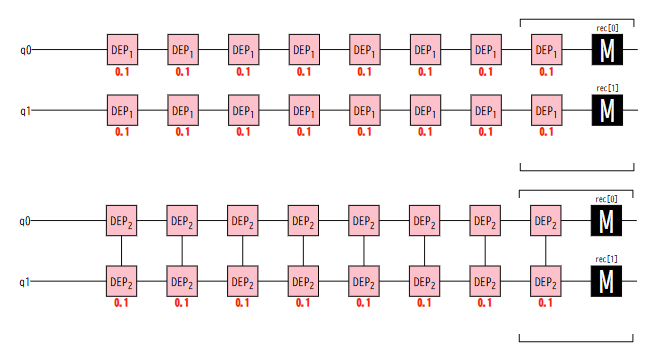
In [47]: T1_dp1 = []
    ...: T1_dp2 = []
    ...: for i in range(32):
    ...:     circuit_dep1 = stim.Circuit()
    ...:     circuit_dep2 = stim.Circuit()
    ...:     for j in range( i ):
    ...:         circuit_dep1.append( 'TICK')
    ...:         circuit_dep2.append( 'TICK')
    ...:         circuit_dep1.append( 'DEPOLARIZE1', 0, 0.1 )
    ...:         circuit_dep1.append( 'DEPOLARIZE1', 1, 0.1 )
    ...:         circuit_dep2.append( 'DEPOLARIZE2', [0,1], 0.1 )
    ...:     circuit_dep1.append('M',[0,1])
    ...:     circuit_dep2.append('M',[0,1])
    ...:
    ...:     sampler = circuit_dep1.compile_sampler()
    ...:     data = np.array( sampler.sample( shots = 2**13 ), dtype = int)
    ...:     q0 = data[ :, 0 ]; q1 = data[ :, 1 ]; p_e = np.sum(q0 | q1) / 2**13
    ...:     T1_dp1.append( p_e )
    ...:
    ...:     sampler = circuit_dep2.compile_sampler()
    ...:     data = np.array( sampler.sample( shots = 2**13 ), dtype = int)
    ...:     q0 = data[ :, 0 ]; q1 = data[ :, 1 ]; p_e = np.sum(q0 | q1) / 2**13
    ...:     p_e = 1 - np.sum(q0 | q1) / 2**10
    ...:     T1_dp2.append( p_e )
In [48]: pl.plot( T1_dp1, label = 'dep1' )
    ...: pl.plot( T1_dp2, label = 'dep2' )
    ...: pl.ylabel( '1 - p(00)')
    ...: pl.xlabel( 'Step')
    ...: pl.legend()
    ...: pl.savefig( '1.svg')

測定値を量子ビット0と量子ビット1に分けてORをとると、どちらかまたは両方1である場合に1となる。つまり p(01) + p(10) + p(11) という確率を得る。その確率は|00>状態で観測さなかった 1 - p(00)という確率であり、図の縦軸にとる。緩和した極限では|00>、|01>、|10>、|11>状態が等確率となるため、1-p(00)は3/4=75%となる。これはこれで良いが、緩和レートがDEPOLARIZE1とDEPOLARIZE2とで異なる。

1ステップあたりの緩和率を測定してみる。先と同様に1-p(00)という|00>状態ではない確率を測定する。

In [49]: circuit_dep1 = stim.Circuit()
    ...: circuit_dep1.append('DEPOLARIZE1', 0, 0.1 )
    ...: circuit_dep1.append('DEPOLARIZE1', 1, 0.1 )
    ...: circuit_dep1.append('M',[0,1])
    ...:
    ...: sampler = circuit_dep1.compile_sampler()
    ...: data = np.array( sampler.sample( shots = 2**20 ), dtype = int)
    ...: q0 = data[ :, 0 ]; q1 = data[ :, 1 ];
    ...: p_edep1 = np.sum(q0 | q1) / 2**20
In [50]: circuit_dep2 = stim.Circuit()
    ...: circuit_dep2.append('DEPOLARIZE2', [0,1], 0.1 )
    ...: circuit_dep2.append('M',[0,1])
    ...: 
    ...: sampler = circuit_dep2.compile_sampler()
    ...: data = np.array( sampler.sample( shots = 2**20 ), dtype = int)
    ...: q0 = data[ :, 0 ]; q1 = data[ :, 1 ];
    ...: p_edep2 = np.sum(q0 | q1) / 2**20
In [51]: [float(p_edep1), float(p_edep2)]
Out[51]: [0.12877273559570312, 0.08009529113769531]

1量子ビット緩和源は緩和率を p = 10 % とすると約 (4/3) * p、2量子ビット緩和源は約 (12/15) * p という値にほぼ一致する。1量子ビットの場合、緩和は1ステップ当たりの緩和率をpとすると(p/3)のXフリップ、(p/3)のYフリップ、(p/3)のZフリップが独立に二つの量子ビットに印加される。2つの量子ビットが独立に緩和するとすると、次の表のようになる。

確率	フリップ軸
(1-p)^2	何もしない
(1-p) p/3	XI
(1-p) p/3	YI
(1-p) p/3	IX
(1-p) p/3	IY
(1-p) p/3	ZI	(00状態に関係ない)
(1-p) p/3	IZ	(00状態に関係ない)
(p/3)^2		(小さいので無視)

ここで2量子ビットのパウリ演算子を {I,X,Y,Z}の積で表記する(順序は量子ビット0、量子ビット1)。ZI軸とIZ軸は反転したとしても初期状態に関係ないため、4/3 p だけがフリップに寄与することになる。上の表は {(1-p)I, p/3 X, p/3 Y, p/3 Z} * {(1-p)I, p/3 X, p/3 Y, p/3 Z} = { (1-p)^2 II, (1-p)p/3 IX, (1-p)p/3 IY, (1-p)p/3 IZ, p/3(1-p) XI, (p/3)^2 XX, ... } とひらすら計算することで得られる。

2量子ビット緩和源は p = 10 % として、次の表の確率でフリップが生じる (IIは何もしない)。15個の成分のうちIZ、ZI, ZZは|00>状態に関係ないことから、12/15 p の確率が緩和に寄与している。シミュレーションから同時並列1量子ビット緩和率と2量子ビット緩和率のサイコロの振り方が若干違うことが分かった(知っていたが)。

	I	X	Y	X
I	(1-p) II	(p/15)IX	(p/15)IY	(p/15)IZ
X	(p/15)XI	(p/15)XX	(p/15)XY	(p/15)XZ
Y	(p/15)YI	(p/15)YX	(p/15)YY	(p/15)YZ
Z	(p/15)ZI	(p/15)ZX	(p/15)ZY	(p/15)ZZ

回路記述表現

StimはPythonのインタフェースの他に、独自の回路表現記述言語を備えている。BNFもここ [5]にあるのでパーザを自分で書くこともできる。せっかくなので使ってみる。

CNOTはCNOT <C> <T> <C> <T> ... のようにして制御量子ビットControl:Cから対象量子ビットTarget:Tに対する命令のようだが、演算が非可換の場合には下のように数珠つなぎのようになる。

In [52]: circuit = stim.Circuit( '''
    ...: H 0
    ...: CNOT 0 1 1 2 2 3 3 4 4 5 5 6 6 7
    ...: ''')
In [53]: circuit.diagram()
Out[53]:
q0: -H-@-------------
       |
q1: ---X-@-----------
         |
q2: -----X-@---------
           |
q3: -------X-@-------
             |
q4: ---------X-@-----
               |
q5: -----------X-@---
                 |
q6: -------------X-@-
                   |
q7: ---------------X-

回路が可換の場合には上手く詰め込むようである。

In [54]: circuit = stim.Circuit( '''
    ...: CNOT 0 1 2 3 4 5 6 7
    ...: CNOT 2 1 4 3 6 5 8 7
    ...: ''')
In [55]: circuit.diagram()
Out[55]:
q0: -@---
     |
q1: -X-X-
       |
q2: -@-@-
     |
q3: -X-X-
       |
q4: -@-@-
     |
q5: -X-X-
       |
q6: -@-@-
     |
q7: -X-X-
       |
q8: ---@-

不出来なGHZ状態生成

GHZ状態は In[52]のようにCNOTを数珠繋ぎにする必要がある。不完全なゲートをシミュレートするたびに、ゲートの後に毎回緩和チャネルを追加する。1量子ビットのアダマールの後には DEPOLARIZE1を、2量子ビットのCNOTの後にはDEPORLARIZE2を追加する。何もしていない間にも量子ビットは緩和するため、1量子ビットゲート実行中暇な際には1量子ビットゲートの緩和率 pdep1 を設定し、2量子ビット実行中に待機している場合には2量子ビットゲートと同じエラー率の pdep2を設定した。
CNOTの数珠つなぎの後に、毎回毎回2量子ビットゲートの緩和を手作業で入れるのが面倒になったので、Pythonインタフェースを使うことにする。回路をテキスト表示するとすごい長い表示となってしまう。

In [56]: pdep1 = 0.005
    ...: pdep2 = 0.03
    ...: circuit = stim.Circuit()
    ...: circuit.append( 'H', 0 )
    ...: for i in range( 8 ):
    ...:     circuit.append('DEPOLARIZE1', i, pdep1 )
    ...: for i in range( 7 ):
    ...:     circuit.append( 'CNOT', [ i, i + 1 ] )
    ...:     circuit.append( 'DEPOLARIZE2',  [ i, i + 1 ], pdep2 )
    ...:     circuit.append( 'DEPOLARIZE1',  [ j for j in range( 8 ) if j != i
    ...: and j != i + 1 ], pdep2 )
    ...: circuit.append( 'M', range( 0, 8 ))
    ...: circuit.diagram()
Out[56]:
q0: -H-DEPOLARIZE1(0.005)-@-DEPOLARIZE2(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-M:rec[0]-
                          | |
q1: ---DEPOLARIZE1(0.005)-X-DEPOLARIZE2(0.03)-@-DEPOLARIZE2(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-M:rec[1]-
                                              | |
q2: ---DEPOLARIZE1(0.005)---DEPOLARIZE1(0.03)-X-DEPOLARIZE2(0.03)-@-DEPOLARIZE2(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-M:rec[2]-
                                                                  | |
q3: ---DEPOLARIZE1(0.005)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-X-DEPOLARIZE2(0.03)-@-DEPOLARIZE2(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-M:rec[3]-
                                                                                      | |
q4: ---DEPOLARIZE1(0.005)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-X-DEPOLARIZE2(0.03)-@-DEPOLARIZE2(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-M:rec[4]-
                                                                                                          | |
q5: ---DEPOLARIZE1(0.005)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-X-DEPOLARIZE2(0.03)-@-DEPOLARIZE2(0.03)---DEPOLARIZE1(0.03)-M:rec[5]-
                                                                                                                              | |
q6: ---DEPOLARIZE1(0.005)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-X-DEPOLARIZE2(0.03)-@-DEPOLARIZE2(0.03)-M:rec[6]-
                                                                                                                                                  | |
q7: ---DEPOLARIZE1(0.005)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)---DEPOLARIZE1(0.03)-X-DEPOLARIZE2(0.03)-M:rec[7]-

結果をシミュレーションしてみる。GHZ状態は |00..0> + |11...1>であるため、8量子ビットだと00000000が50%の確率で、11111111が50%の確率で観測されることが理想的である。今回は雑音を入れている結果が期待される。

Out[60]に示すようにデータは[Q0,Q1,Q2,...]というビット列として得られる。このままではデータ処理が面倒なため、これらを2進数だとみなしてQ0をLSBとして Q7Q6..Q1Q0の順に10進数にエンコードする。エンコードに必要なビットシフト演算子がIn[58]で定義されており、In[61]とIn[63]においてエンコードしている。Out[62]に示すように、データは適切にビットシフトされており、In[63]で行方向に足し算することで Q7Q6..Q0 を2進数とみなして並べた10進数のデータ列が得られる (Out[64]の結果)。測定結果00000000は0、測定結果 11111111 は255としてエンコードされるため、理想的には0が50%、255が50%で得られるはずである。

In [57]: sampler = circuit.compile_sampler()
In [58]: lshift = np.array( [2 ** i for i in range( 8 )], dtype=int )
In [59]: data = np.array( sampler.sample( shots = 2**20 ), dtype=int )
In [60]: data
Out[60]:
array([[0, 0, 0, ..., 1, 1, 1],
       [1, 1, 1, ..., 1, 1, 1],
       ...,
       [0, 0, 0, ..., 0, 0, 0]])
In [61]: data_enc = lshift * data
In [62]: data_enc
Out[62]:
array([[  0,   0,   0, ...,  32,  64, 128],
       [  1,   2,   4, ...,  32,  64, 128],
       ...,
       [  0,   0,   0, ...,   0,   0,   0]])
In [63]: data_sum = np.sum( data_enc, axis = 1 )
In [64]: data_sum
Out[64]: array([224, 255,  31, ..., 255, 253,   0])
In [65]: hist, bins = np.histogram( data_sum, bins = range( 255 + 2 ))
In [66]: hist / 2**20
Out[66]:
array([1.86561584e-01, 2.85034180e-02, 2.17609406e-02, 1.14555359e-02,
...
       1.16233826e-02, 2.15415955e-02, 2.85158157e-02, 1.86426163e-01])
In [67]: pl.plot( bins[ 1 : ], hist / 2**20, 'o-' )
In [68]: pl.xlabel( 'Measurement outcome')
In [69]: pl.ylabel( 'Probability' )
In [70]: pl.savefig( '1.svg' )

結果は下の図の通りである。Out[66]の測定結果をサンプリング回数2^20で割った確率をみると、配列の0番目が00000000の確率で19%、配列の末尾が11111111の確率で19%と他と比べて確率は高いものの、20%程度にどどまった。緩和が入っているため、ビットフリップや位相フリップ、2量子ビットゲートエラーにより緩和したものと考えられる。

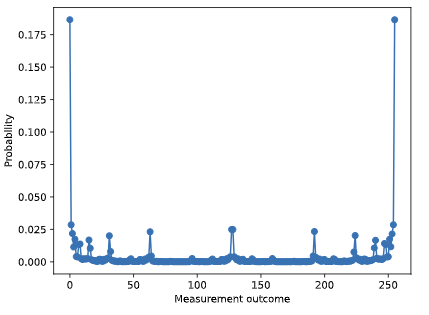
次に1回のサンプリング中に何回1が出てきたのかを数えてみる、理想的には1が0回が50%、1が8回が50%が得られるはずである。得られた測定値を2進数エンコードなしにIn[73]のように行方向に足し上げてみると、Out[74]のように0~8の値のデータ列を得る。ヒストグラムを下図に示す。

In [71]: sampler = circuit.compile_sampler()
In [72]: data = np.array(sampler.sample( shots = 2**20 ), dtype=int )
In [73]: data_sum = np.sum( data, axis = 1 )
In [74]: data_sum
Out[74]: array([8, 7, 1, ..., 7, 3, 8])
In [75]: pl.hist(data_sum, bins=range( 8 + 2 ), density=True )
Out[75]:
(array([0.18557644, 0.1297121 , 0.07934856, 0.06985188, 0.0695715 ,
        0.06998539, 0.08014584, 0.12971878, 0.18608952]),
 array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.]),
In [76]: pl.savefig( '1.svg' )

これを見ると全体の中で少なくない確率で(Out[75]の結果でも確認できる)、結果に1ビット誤りが生じているものが13%+3%で約26%程度、2ビットの誤りが生じているものが、8%+8%=16%程度生じていることが分かる。

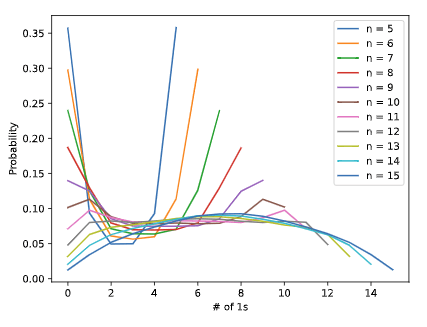
そう考えると、これが量子ビット数が大きくなるとどう分布が変化するのか気になってくる。Stimはクリフォードシミュレータなので量子ビット数が大きくなっても気にせずに計算できる。5ビットから15ビットまでの分布の依存性を取ると下図のようになる。

In [77]: pdep1 = 0.005
    ...: pdep2 = 0.03
In [78]: for n in range( 5, 16 ):
    ...:     circuit = stim.Circuit()
    ...:     circuit.append( 'H', 0 )
    ...:     for i in range( n ):
    ...:         circuit.append('DEPOLARIZE1', i, pdep1 )
    ...:     for i in range( n - 1 ):
    ...:         circuit.append( 'CNOT', [ i, i + 1 ] )
    ...:         circuit.append( 'DEPOLARIZE2',  [ i, i + 1 ], pdep2 )
    ...:         circuit.append( 'DEPOLARIZE1',  [ j for j in range( n ) if j != i and j != i + 1 ], pdep2 )
    ...:     circuit.append( 'M', range(0, n ))
    ...:     
    ...:     sampler = circuit.compile_sampler()
    ...:     data = np.array( sampler.sample( shots = 2**20 ), dtype=int )
    ...:     data_sum = np.sum( data, axis = 1 )
    ...:     hist, bins = np.histogram( data_sum, bins = range( n + 2 ))
    ...:     pl.plot( bins[:-1], hist / 2**20, label = 'n = {}'.format( n ))
    ...: 
    ...: pl.legend()
    ...: pl.xlabel( '# of 1s' )
    ...: pl.ylabel( 'Probability' )
    ...: pl.savefig( '1.svg' )

回路が大きくなると、やがて2項分布のようになっていくことが分かる。

参考文献

[1] Stim, github
[2] Craig Gidney, Stim : a fast stabilizer circuit simulator, Quantum 5, 497 (2021).
[3] クリフォード群, Wikipedia
[4] Quantattack, GitHub
[5] Stim Circuit File Format (.stim), GitHub
[6] Gates supported by Stim, GitHub