DeepSeek-R1 (V3) のアーキテクチャの解説
この記事について
この記事では DeepSeek-R1 および DeepSeek-V3 のアーキテクチャについて解説します。DeepSeek-R1 は DeepSeek-V3 の事前学習済みモデルに追加学習を施したものなので、アーキテクチャはどちらも同じです。
主に DeepSeek-V3 Technical Report の §2 の内容に沿ってまとめていきます。理解に必要な基礎知識 (特に Attention について) は補足するので、ニューラルネットワークの基本的な知識があれば読めると思います。また、なるべく集合論的な曖昧さがないように書いているので、数学に慣れている人は読みやすいと思います。
元々は DeepSeek-V3 Technical Report および R1 の論文をまとめるつもりでしたが、あまりにも長くなってしまうので分割して、この記事ではアーキテクチャのみを解説することにしました。以下のタイトルの記事も執筆予定です。
-
アーキテクチャについて
- DeepSeek-R1 (V3) のアーキテクチャ ← この記事
- Attention の基礎から DeepSeek MLA (Multi-Head Latent Attention) を解説する
- DeepSeek MoE (Mixture of Experts) の解説
-
学習方法について
- DeepSeek-R1 (V3) の事前学習方法について
- DeepSeek-R1 と V3 の事後学習方法の違い
- DeepSeek-R1 の強化学習手法 GRPO を強化学習基礎から解説する
-
DeepSeek-R1 の凄いところまとめ
語句説明
この記事を読むにあたって重要となる語句をまとめます。
-
DeepSeek-V3
- DeepSeek から 2024年12月に発表された LLM モデル
-
DeepSeek-R1
- DeepSeek から 2025年1月に発表されて話題になった LLM モデル
- DeepSeek-V3 の事前学習済モデルをベースに学習方法を工夫したもの
-
MLA (Multi-head Latent Attention)
- Multi-Head Attention の一部を Latent space (潜在空間) に置き換えたもの
- 推論時に必要なキャッシュの量を削減させる
-
MoE (Mixture-of-Experts)
- 入力に応じて適切なネットワークに処理を振り分けるもの
- 学習を効率化させる役割を持つ
アーキテクチャ全体像
DeepSeek-V3 のアーキテクチャは基本的に以下の図の通りで、Transformer Block というものがいくつか連なったものになっています。正確には入力側に文章をベクトル化するための Tokenizer と Embedding があり、出力側にはその逆操作をする層が加わります。

DeepSeek-V3 Technical Reportから引用
ポイントは上図の右にある MLA と DeepSeekMoE です。MLA では、MultiHead Attention の性能を落とさずに
- 推論時の計算量を抑えるための KV-Cache という仕組みに必要なメモリ量の大幅な削減
に成功したようです。DeepSeekMoE では、入力に応じて処理をさせるネットワーク (専門家と呼ばれる) を選択する MoE (専門家の混在) と呼ばれる仕組みの
- 各専門家が共通の知識を獲得しようとする懸念の解消
- 学習時に特定の専門家にのみ振り分けられる問題の解消方法 (Load Balancing) の改善
に成功したようです。
この記事では
- Tokenizer
- Embedding
- RMS Normalization
- Multi-Head Latent Attention (MLA)
- DeepSeekMoE (Mixture of Experts)
- 最後の出力の処理
についてまとめます。1, 2, 3, 6 は割と一般的なもので、4, 5 は DeepSeek オリジナルの要素が含まれています (4, 5 は別の記事で詳しく解説します)。token 間の関係についての処理は Attention のみで行い、それ以外は token ごとに処理をすることを念頭におくと理解しやすいと思います。

また、上の図のようにブロックの入力の前で分岐して出力後に合流する矢印がありますが、これは skip connection といって学習の際の勾配消失問題を解消する役割を持ち、これによって深い層のネットワークの学習が可能になります。skip connection についてはこの記事では解説しません。
Tokenizer について
まずは入力の最初の処理である Tokenizer について説明します。
Tokenizer とは
Tokenizer とは文章を token と呼ばれる単位に分割する役割を持つものの事です。例えば
「吾輩は猫である。名前はまだ無い。」
という文章を単語単位で分割すると
"吾輩は猫である。名前はまだ無い。"
↓
['吾輩', 'は', '猫', 'で', 'ある', '。', '名前', 'は', 'まだ', '無い', '。']
のように文章が分割されます。他にも文字単位で分割する方法も考えられます。どの単位を token とするかはケースバイケースです。
文章を token の列に分割することを token 化 (tokenize) と言います。ニューラルネットワーク上ではこのように文章を token 化した後、各 token に識別番号をふり、文章を番号列として扱います。
一般に、ネットワークが扱うことのできる token 数が多くなると計算コストや必要なメモリが増加します。一方、token 数が少なくなると
- 文章が細かく分割されすぎて意味のあるテキスト表現を学習しにくい
- 分割後の token 列が長くなる
などの問題が起きます。
その間をとって、粗すぎず細かすぎず、いい感じの分割を行う方法がいくつか知られています (例えば npaka さんの記事を見てください)。
また、文字列を単語の列ではなく byte の列とみなす手法もあり、そのようにすることで原理的にどんな言語でも受け付けられるようになります。
DeepSeek の tokenizer ではありませんが、Llama の tokenizer のデモが公開されています。難しめの漢字を入力すると byte 単位で分割されることが確認できます。
DeepSeek-V3 の Tokenizer
Tokenizer についての論文中の記述はそれほど詳しくないので、わかる部分だけまとめます。この節は読み飛ばしてもアーキテクチャの理解に影響ありません。
まず、DeepSeek-V3 の Tokenizer は BBPE というアルゴリズムを採用しています。分割の最小単位は文字ではなく byte なので原理的にはどんな言語でも受け付けます。
V3 の Technical Report には V2 の Tokenizer からの変更点のみ書かれているので、まずは V2 の Tokenizer[1] に書かれているもの についてまとめます。
- 改行、句読点、CJK記号の併合を防ぐために、GPT-2 と同様に事前トークン化を行なった。
- 数字は1桁ずつに分割した。
- 約 24 GB の多言語コーパスでトレーニングした。
- これまでの経験から、トークンの数を 10万 (102,400) とした。
- さらに15個の特殊なトークンを追加した。
V3 の Tokenizer は上記から以下のような変更を加えたようです。
- トレーニングコーパスについて
- 数学サンプルとプログラミングサンプルの比率向上
- 英語、中国語以外の言語の比率向上
- プレトークナイザーとトレーニングデータを、多言語圧縮効率を最適化するように変更
- トークンの数を 128K (コードをみる限り 129280) とした。
- V2 とは異なり、改行、句読点が含まれる token を禁止しなかった
- これによりトークン境界バイアス[2]が発生する可能性があるため、改行、句読点などが含まれる token を学習時にランダムで分割した
- トークン境界バイアスとは学習時に想定していなかった token の分割が推論時に行われると推論が不安定になる現象のこと
- これによりトークン境界バイアス[2]が発生する可能性があるため、改行、句読点などが含まれる token を学習時にランダムで分割した
Tokenizer の数学的な記号の準備
この後の説明のために、Tokenizer を数学的に、というよりも集合論的に、集合と写像を用いて表します。まず文章
のことであるとし、文章全体の集合を
有限部分集合
token の集合
token の集合
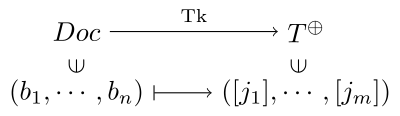
token の集合
ちなみに
Embedding (単語埋め込み)
Embedding (単語埋め込み) とは
Embedding では token を低次元のベクトル空間
まず token

このようなベクトルを one-hot ベクトルといい、
で表すこととします。
Embedding は線形写像

で与えられます。ここで、
以後、線型写像を
tonek の列に対しては、token 毎に埋め込みます。

単語埋め込みが線形であることの補足
ニューラルネットワークでは非線形性を持たせるために活性化関数と呼ばれるものを用いますが、言語の意味に関する処理を行う場合は活性化関数を用いずに、線形な変換のみを行う場合が多いです。それはおそらく、単語間の意味がある種の線形性を持つと考えられているからです。
それは2013年に発表された Word2Vec と呼ばれるモデルにおいて、おそらく最初に確認されました。有名なのは
「王」-「男」+「女」=「女王」
という式で、Word2Vec により埋め込まれた単語ベクトル空間の中で左辺を計算すると、「女王」の単語ベクトルに近い値になります。(ちなみに近さはベクトルの成す角度のみで測るのでベクトルの大きさは関係なく、正確には線形性とはいいません。)
活性化関数を用いると線形性が崩れてしまい、単語間の意味が失われる可能性があるため、 Attention においても線形な変換が主に用いられるのだと思います。
RMS Normalization について
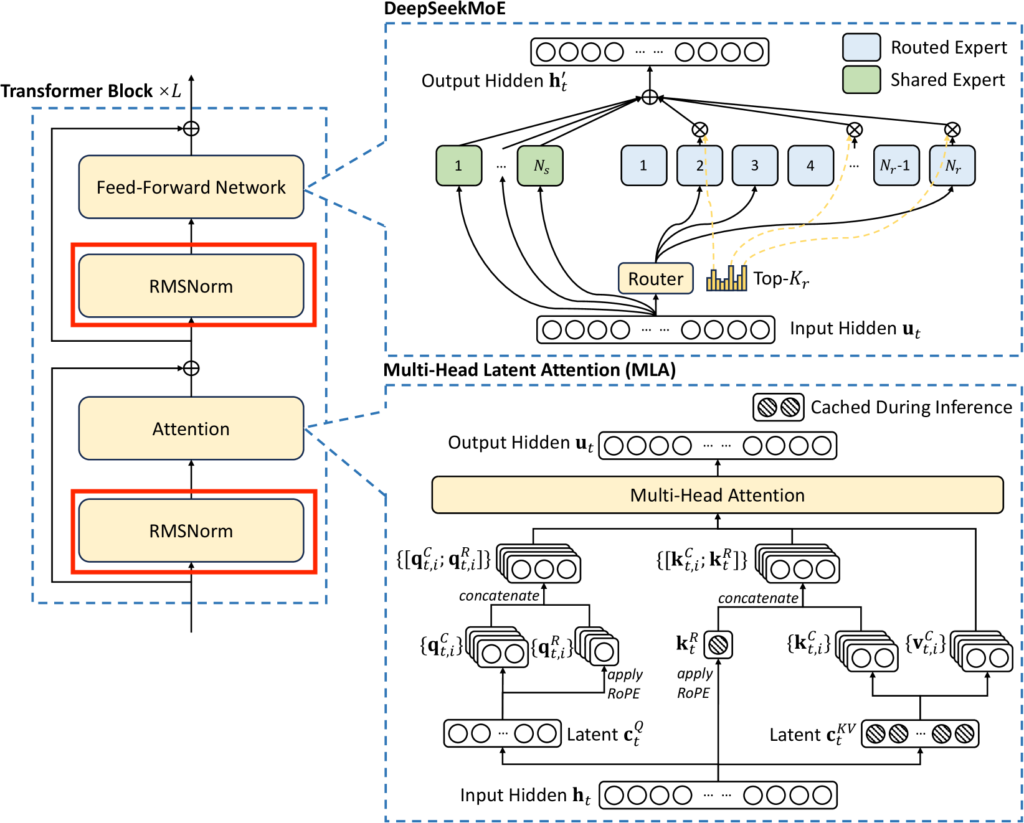
ここからは Transformer Block の中身の解説になります。Transformer Block の入力と出力の形式は、長さ
と同じ形式ですが、Attention 以外は token の位置毎に処理されます。それを念頭に置くと理解しやすくなるかもしれません。
以後、Transformer Block の入力データについては位置の添字になるべく
Normalization はデータのスケールを調整して学習を安定させる役割を持ちます。まずは、RMS Normalization のベースとなった Layer Normalization について説明します。
Layer Normalization とは
一般にデータ
に対して、平均
を計算し、
に置き換えると
と変換します。
RMS Normalization とは
RMS Normalization は Layer Normalization の性能を落とさずに処理を簡略化したものです。RMS は Root Mean Square の略で、Layer Normalization における平均を取ることによるデータの中心化を省略し、分散の代わりに 2 乗の平均の平方根を取ったものになります。
つまり、入力データ
と
と変換します。
DeepSeek のアーキテクチャにおける RMS Normalization への入力データの形は、入力された token の数を
となります。例えば Embedding 直後では、各 token の埋め込みベクトル
が入力データとなります。これに対して RMS Normalization を、各 token の位置毎に適用します。つまり
に対して
と定めます。ただし
MultiHead Latent Attention (MLA)
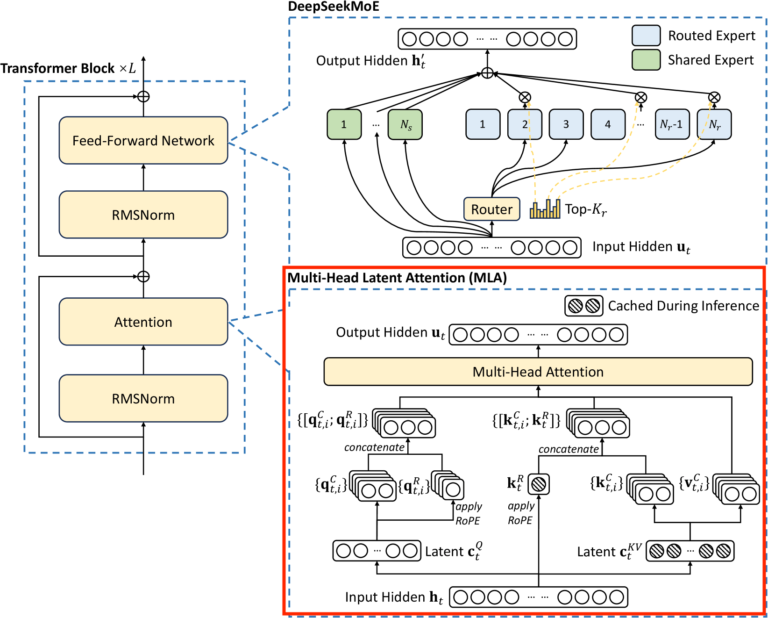
MultiHead Latent Attention (MLA) については記事を分けて、以下の記事で解説します。
「Attention の基礎から DeepSeek MLA (Multi-Head Latent Attention) を解説する」
要点だけまとめると以下のようになります。
- 推論時にキャッシュされる情報の次元を低くする (Latent Space に埋め込む) ことでキャッシュ量を減らした
- キャッシュ量を減らしたが、精度は落ちていない
- Latent Space に埋め込む影響で Position Encoding のやり方が少し特殊
DeepSeekMoE (Mixture of Experts)
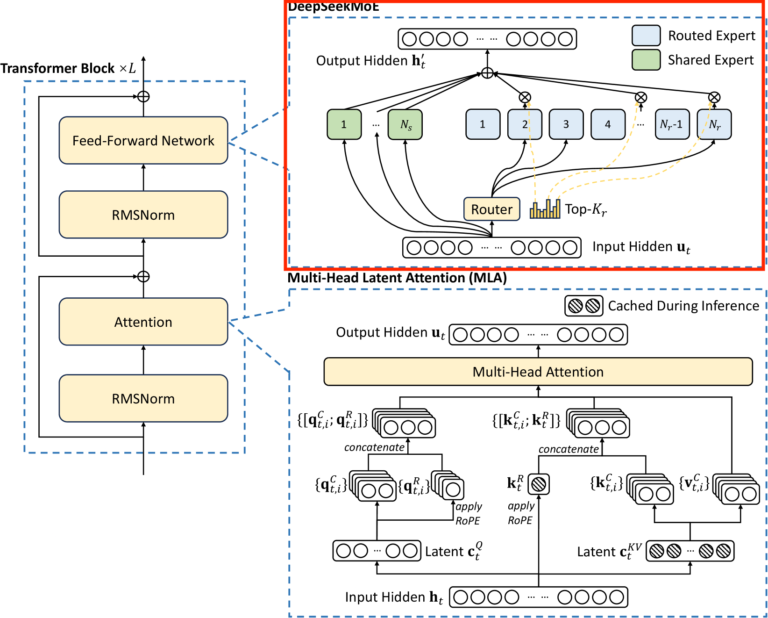
DeepSeekMoE については記事を分けて、以下の記事で解説します。
「DeepSeek MoE (Mixture of Experts) の解説」
要点だけまとめると以下のようになります。
- shared expert と呼ばれる、常に処理を行う expert を入れることで、各 expert が共通の知識を獲得しようとする冗長性を解消し、各 expert をより専門化させた。
- 従来使われていた損失関数を使わないことで、学習を効率化。
出力部分
以上で Transfomer Block 内の説明が終わったので、最後に出力の部分の処理について説明します。最後に出力の部分では、Transfomer Block の出力
の各
そのために、線型写像
と、
ただし
で定義される関数です。
学習時はこの確率分布を使って損失関数を計算し、推論時は確率の最も高い token を選ぶか、確率分布に従ってサンプリングを行います (損失関数については事前学習の記事で書きます。)。
変形される場合があります。
以上で、DeepSeek-R1 (V3) のアーキテクチャを一通り説明できました。
Discussion