Attention の基礎から始める DeepSeek MLA (Multi-Head Latent Attention) の解説

本記事では DeepSeek-V3 Technical Report の §2 の内容に沿って、DeepSeek-R1 (V3) で用いられているアーキテクチャの 1 つである、MLA (Multi-Head Latent Attention) について解説します。

まず最初に、MLA の基礎であり、自然言語モデルでよく用いられる Attention や MultiHead Attention について詳しく説明しますので、ニューラルネットワークの基本的な知識があればこの記事を読むことができると思います。

この記事の内容は「DeepSeek-R1 (V3) のアーキテクチャ」から分岐したものです。基本的にはこの記事のみで完結するよう記述するつもりですが、tokenizer と token の埋め込みについては上記の記事を参照してください。

以下の図は DeepSeek-R1 (V3) の Transformer Block の全体像になります。赤枠で囲っている部分をこの記事で解説します。

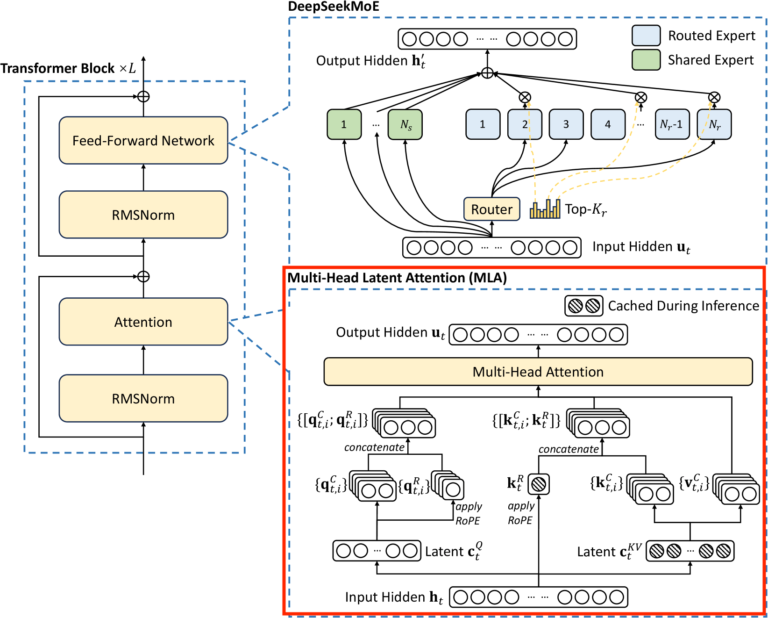
DeepSeek-V3 Technical Reportから引用

そもそも Attention とは

Attention とは、どの情報に注目すべきかを判断するための仕組みです。例えば「これはペンです。」という文章を英語に訳するタスクを行い、"This is a" まで訳できたとします。この次に来るであろう単語 "pen" を推測するのに、「これはペンです。」のうちどの部分に注目すべきか、ということを判断します。

このようなタスクをこなす場合、ネットワークには下の図の下部のような token の列を入力し、図の上部のような token の列を出力させます。ただし [sos] は文章の始まりを意味する特殊な token であり、[delim] は文章の区切りを意味する特殊な token です。

$$\begin{CD} {\color{lightgray}これ} @. {\color{lightgray}は} @. {\color{lightgray}ペン} @. {\color{lightgray}です} @. {\color{lightgray}。} @. {\color{lightgray}[\textrm{delim}]} @. \textrm{this} @. \textrm{is} @. \textrm{a} @. {\color{red}?} \\ @AAA @AAA @AAA @AAA @AAA @AAA@AAA @AAA @AAA @AAA\\ [sos] @. これ @. は @. ペン @. です @. 。 @. [\textrm{delim}] @. \textrm{this} @. \textrm{is} @. \textrm{a} \end{CD}$$

翻訳の流れは、まず「[sos] これ は ペン です 。 [delim]」までを入力し、[delim] の次の token を予測させます。その後予測した token を入力の右に繋げて再びその次の token を予測させ、、、ということを繰り返すことで文章を生成します。グレーの部分は出力させる場合もさせない場合もあります。

Attention の役割は、"a" の次の単語を予測するのに、図の下部の入力のどの部分に注目すれば良いのかを与えることです。

Attention の考え方

簡単のため日本語部分と英語部分を分け、日本語部分を token 化 (+ 埋め込み) をしたベクトル列を

$$(x_1, \cdots, x_n) \in (\mathbb{R}^{d_{emb}})^{n}$$

英語部分を token 化したものを

$$(y_1, \cdots, y_m) \in (\mathbb{R}^{d_{emb}})^{m}$$

とおき、"a" の埋め込みベクトルは $y_m$ であるとします。$d_{emb}$ は埋め込みベクトルの次元です。また、埋め込みベクトルは縦ベクトルで表すこととします (行列を右から作用させるために縦ベクトルにしていますが、論文によっては横ベクトルを用いているので注意してください)。

単語埋め込み空間では内積により token 近さを測ることができると考えられているので、$y_m$ と $x_i$ の内積をとって大きいものに注目する、という方法が考えられますが、必要なのは "a" そのものではなく "a" の次に来そうな単語です。

そこで、$y_m$ を別のベクトルへ変換し、それが次の単語の情報を持つことを期待します。ベクトルの変換は線型写像 $W^Q: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d_q}$ で与えます。一般には $d_{emb} \neq d_q$ です。

単語の近さを測るために、$W^Qy_m$ と $x_i$ の内積を取りたいですが、次元が異なるので $x_i$ も $d_q$ 次元のベクトルに変換する必要があります。ただし $x_i$ の埋め込みは次の単語と関係ないので、$x$ と $y$ で別の埋め込み方が与えられるべきです。$x_i$ の変換を線型写像 $W^K: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d_q}$ で与えます。

$W^Q y_m$ と $W^K x_i$ との内積の値を $a_i = W^Q y_m \cdot W^K x_i$ とおくと

$$(a_1, \cdots, a_n) \in \mathbb{R}^n$$

が得られます。$a_i$ は $y_m$ の $x_i$ への注目度を表現していると考えられ、$a_i$ が大きいほど注目度が高いと考えられます。

$(a_1, \cdots, a_n)$ の $\textrm{softmax}$ を取とって $0 \sim 1$ の値に正規化したものを $(\overline{a}_1, \cdots, \overline{a}_n)$ とおきます。$\sum_{i=1}^{n} \overline{a}_i x_i$ は入力 token のうち $\overline{a}_i$ が大きい token が強調されたベクトルになります。

それに線形写像 $W^V: \mathrm{R}^{d_{emb}} \to \mathrm{R}^{d_v}$ を適用した

$$W^V \left(\sum_{n=1}^{n} \overline{a}_i x_i \right) = \sum_{n=1}^{n} \overline{a}_i W^V x_i$$

を用いて次の token を予測します。ちなみに $W^V$ による $x_i$ の変換は注目度を計算する前に行っても後に行っても同じです。

Attention の式

一般的な用語に合わせて Attention を説明し、式を整理します。

$(y_1, \cdots, y_m) \in (\mathbb{R}^{d_{Input}})^m$ を Input, $(x_1, \cdots, x_n) \in (\mathbb{R}^{d_{Mem}})^n$ を Momery と呼びます。 さっきの例だと英語の文章が Input、日本語の文章が Momery に相当します。$y_i$ は $d_{Input}$ 次元、$x_i$ は $d_{Mem}$ 次元ベクトルとします。

線形写像 $W^Q: \mathbb{R}^{d_{Input}} \to \mathbb{R}^{d_q}$, $W^K: \mathbb{R}^{d_{Mem}} \to \mathbb{R}^{d_q}$, $W^V: \mathbb{R}^{d_{Mem}} \to \mathbb{R}^{d_v}$ に対して

$$\begin{align*} q_i &= W^Q y_i \quad (1 \leq i \leq m) \\ k_i &= W^K x_i \quad (1 \leq i \leq n) \\ v_i &= W^V x_i \quad (1 \leq i \leq n) \end{align*}$$

とおいて、$q_i$ を query、$k_i$ を key、$v_i$ を value といいます。$W^Q, W^K, W^V$ はバイアスなしの線形層で与えられます。このとき

$$\begin{align*} Q &= (q_1, q_2, \cdots, q_m) \\[.3em] K &= (k_1, k_2, \cdots, k_n) \\[.3em] V &= (v_1, v_2, \cdots, v_n) \end{align*}$$(縦ベクトルを横に並べた行列)

$$\mathrm{Attention}(Q, K, V) = V \ \mathrm{softmax} \left(\frac{{}^t K Q}{\sqrt{d_q}}\right)$$

で与えられます。${}^t K$ は $K$ の転置行列です (埋め込みベクトルを縦ベクトルとした影響で式の形が標準のものと少し違っています)。$\sqrt{d_q}$ で割っているところだけさっきと異なります。

ひとつひとつ見ていくと ${}^t K Q$ は

$${}^t K Q = \begin{pmatrix} k_1 \cdot q_1 & k_1 \cdot q_2 & \cdots & k_1 \cdot q_m\\ k_2 \cdot q_1 & k_2 \cdot q_2 & \cdots & k_2 \cdot q_m\\ \vdots & & \ddots & \vdots \\ k_n \cdot q_1 & k_n \cdot q_2 & \cdots & k_n \cdot q_m \end{pmatrix}$$

であり、最後の列 (縦の並び) に注目すれば、さっきの例でいう $y_m$ に対応する注目度に相当します。

$\sqrt{d_q}$ で割っていることに関しては、$\mathrm{softmax}$ を取る際に中身が大きくなると学習効率が落ちる (勾配が小さくなる) ことを防ぐためのようです。$1$ が $d_q$ 個並んだベクトル $(1, 1, \cdots, 1)$ のベクトルの長さが $\sqrt{d_q}$ であり、次元が大きいほど (適当に取った) ベクトルの長さが長くなる傾向があります。

$\mathrm{softmax}$ は列毎に (縦をひとまとまりとして) 取ります。

最後に

$$\mathrm{softmax} \left(\frac{{}^t K Q}{\sqrt{d_q}}\right) = \begin{pmatrix} \overline{a}_{11} & \overline{a}_{12} & \cdots & \overline{a}_{1m}\\ \overline{a}_{21} & \overline{a}_{22} & \cdots & \overline{a}_{2m}\\ \vdots & & \ddots & \vdots \\ \overline{a}_{n1} & \overline{a}_{n2} & \cdots & \overline{a}_{nm} \end{pmatrix}$$

とおけば

$$V\ \mathrm{softmax} \left(\frac{{}^t K Q}{\sqrt{q}}\right) = \left(\sum_{i=1}^n \overline{a}_{i1}v_i , \sum_{i=1}^n \overline{a}_{i2}v_i, \cdots, \sum_{i=1}^n \overline{a}_{im}v_i \right)$$

となります。翻訳の例で言えば、$q_j$ の次の token を予測するのに用いられるベクトルが $\sum_{i=1}^n \overline{a}_{i j}v_i$ になります。

Attention 出力は $d_v$ 次元ベクトルが $m$ 個並んだものになるので、入力と次元を合わせるなら $d_v = d_{Input}$ とすれば良いです。skip connection を付加することが多いため、$d_{Input} = d_{emb}$ (token の埋め込みの次元) であることが多いようです。

ちなみに $v_i = W^V x_i$ であり、$X$ を $x_i$ を横に並べた行列とすると行列の積の結合性から

$$(W^V X) \ \mathrm{softmax} \left(\frac{{}^t K Q}{\sqrt{q}}\right) = W^V \left(X \ \mathrm{softmax} \left(\frac{{}^t K Q}{\sqrt{q}}\right) \right)$$

が成り立つので、$W^V$ の役割は単に最後に線形変換をかけているだけであり、本質は key と query により注目度を計算するところにあります。

self-Attention とは

Input と Memory が同じとき、self-Attention と言います。Input と Memory が分かれている場合は Memory への注目度しか計算していませんでしたが、self-Attention ではその区別がなくなるので Input (= Memory) の全ての token に対して注目度を計算します。

MultiHead Attention とは

MultiHead Attention とは、Attention を複数並列に用意して、その出力を連結して、線形変換を施すものです。具体的には以下のようにします。

先ほどと同様に Input を $y \in (\mathbb{R}^{d_{Input}})^m$, $y = (y_1, \cdots, y_m)$、Memory を $x \in (\mathbb{R}^{d_{Mem}})^n$, $x = (x_1, \cdots, x_n)$ とします。そして $n_h$ をある自然数として $3 \times n_h$ 個の線形変換

$$\begin{align*} W^Q_h&: \mathbb{R}^{d_{Input}} \to \mathbb{R}^{d_{q_h}} \quad (1 \leq h \leq n_h) \\ W^K_h&: \mathbb{R}^{d_{Mem}} \to \mathbb{R}^{d_{q_h}} \quad (1 \leq h \leq n_h) \\ W^V_h &: \mathbb{R}^{d_{Mem}} \to \mathbb{R}^{d_{v_h}} \quad (1 \leq h \leq n_h) \end{align*}$$

を考えます。そして $n_h$ 個の Attention

$$o_h = \mathrm{Attention}(W^Q_h y , W^K_h x, W^V_h x) \quad (1 \leq h \leq n_h)$$

を考えます。$o_h$ は $d_{v_h}$ 次元の縦ベクトルを横に $n$ 個 (Memory の長さ分) 並べたものです。

$o_h$ を縦に連結した

$$A = \mathrm{vconcat}(o_1, \cdots, o_{n_h})$$

は $\sum_{h=1}^{n_h} d_{v_h}$ 次元の縦ベクトルを横に $n$ 個並べたものになります。これの各列成分に線形変換 $W^O: \mathbb{R}^{\sum_{h=1}^{n_h} d_{v_h}} \to \mathbb{R}^{d_o}$ を施したものが MultiHead Attention の出力となります。$W_O$ はバイアスなしの線形層として与えられます。

普通は $d_o = d_{emb}$, $d_{v_h} = d_{emb} / h$ とします。

RoPE (Rotary Positional Embeddings) とは

Attention の計算は入力された token と key の内積をとって和を取るだけで、かつ線形変換は token の位置毎に行われるため、token の順序を認識できません。token の順番を入れ替えて Attention を計算しても、出力結果は元の順番での計算結果の順番を入れ替えた物になるだけです。

そこで Positional Embedding という方法で token 位置情報を付加します。まずは初期に考えられた手法を説明し、その後 DeepSeek-R1 (V3) でも用いられている RoPE について説明します。

Absolute Positional Embedding

初期に考えられた Absolute Positional Embedding は以下のとおりです。

$(x_1, \cdots, x_n) \in (\mathbb{R}^{d_{emb}})^n$ を token の埋め込みの列とし、$j$ 番目のベクトル $x_j$ を

$$x_j = \begin{pmatrix}x_{j, 1} \\ \vdots \\ x_{j, d_{emb}} \end{pmatrix} \in \mathbb{R}^{d_{emb}}$$

と表します。また、$p_{j, i} \in \mathbb{R}$ を

$$\begin{align*} p_{j, 2i} &= \sin \left(\frac{j}{10000^{2i/d_{emb}}}\right) \\ p_{j, 2i+1} &= \cos \left(\frac{j}{10000^{2i/d_{emb}}}\right) \end{align*}$$

とおいて位置を表すベクトル $p_j \in \mathbb{R}^{d_{emb}}$ を

$$p_j = \begin{pmatrix}p_{j, 1} \\ p_{j, 2}\\ \vdots \\ p_{j, d_{emb}} \end{pmatrix}$$

と定めます。$(p_{j,2i}, p_{j, 2i+1})$ は円周上の点であり、$i$ が大きくなるほど角度が小さくなり $0$ に近づきます。また $j$ が大きいほど多く回転します。

そして

$$(x_1, \cdots, x_n) + (p_1, \cdots, p_n) = (x_1 + p_1, \cdots, x_n + p_n)$$

と位置を表すベクトルを足すことで token の埋め込みの列に位置情報を付加します (右辺の $+$ は $\mathbb{R}^{d_{emb}}$ 上のベクトルとしての和です)。

RoPE

Absolute Positional Embedding は Attention の入力前に行いますが、実際に Attention に重要なのは query と key の位置関係だけで、value には必要ありません。また、文章が長くなるほど絶対的な位置よりも相対的な位置関係が明確になる方が好ましいと考えられます。RoPE はこの 2 つの性質を持ちます。

RoPE は Attention の内部で行います。まず、以下の行列

$$\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}$$

は、縦ベクトルに左から作用させることで、平面を反時計回りに $\theta$ (ラジアン) 回転させることに注意します。また、この行列の転置は逆回転の行列になります。

query と key の次元 $d_q$ が偶数であると仮定して

$$\theta_i = \frac{1}{10000^{2(i-1) / d_q}}$$

とおき、

$$R_{j} = \begin{pmatrix} \cos j \theta_1 & -\sin j \theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin j \theta_1 & \cos j \theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos j \theta_2 & -\sin j\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin j \theta_2 & \cos j \theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos j \theta_{\frac{d_q}{2}} & -\sin j \theta_{\frac{d_q}{2}} \\ 0 & 0 & 0 & 0 & \cdots & \sin j \theta_{\frac{d_q}{2}} & \cos j \theta_{\frac{d_q}{2}} \end{pmatrix}$$

という行列を考えます。これは $d_q$ 次元のベクトルを $2$ 次元ずつに分けて、それぞれ時計回りに $j \theta_i$ 回転させる行列を表します。

$(x_1, \cdots, x_n) \in (\mathbb{R}^{d_{emb}})^n$ を self-Attention の Input (かつ Memory) とし、$W^Q: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d_q}$ を query への線形写像、$W^K: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d_q}$ を key への線形写像とします。$j$ 番目の query、$\ell$ 番目の key をそれぞれ

$$\begin{align*} \overline{q}_j &= R_j q_j = R_j W^Q x_j \\ \overline{k}_{\ell} &= R_{\ell}k_{\ell} = R_{\ell} W^K x_{\ell} \end{align*}$$

と $R_j$, $R_{\ell}$ で回転させます。すると $\overline{k}_{\ell}$ と $\overline{q}_j$ の内積は

$$\begin{align*} \overline{k}_{\ell} \cdot \overline{q}_j &= {}^t(R_{\ell} k_{\ell}) R_j q_j\\ &= {}^t k_{\ell} \, {}^tR_{\ell} R_{j} q_j \\ &= {}^t k_{\ell} R_{j-\ell} \, q_{j} \\ \end{align*}$$

となり、$k_{\ell}$ と $q_j$ の間に行列 $R_{j -\ell}$ が挟まります。ただし転置は逆回転なので ${}^tR_\ell = R_{-\ell}$ です。

$R_{j -\ell}$ は $j$ と $\ell$ の相対的な位置で決まるという特徴があり、また $|j -\ell|$ が大きくなるほど　$\overline{k}_{\ell} \cdot \overline{q}_j$ の値が小さくなることが知られています (long-term decay)。これにより、比較的遠い位置にある単語同士の attention は小さくなります。long-term decay は式変形により証明されています^[1]が、完全な証明にはなっていません。

MultiHead Latent Attention (MLA) とは

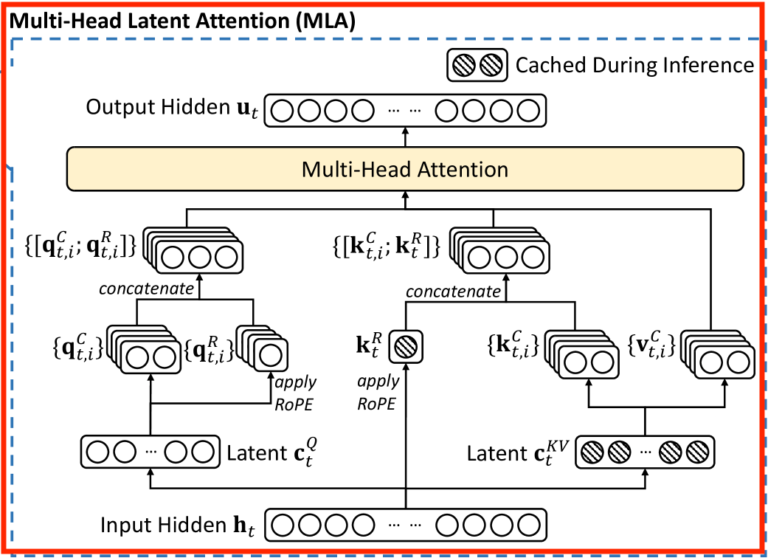
ここからは本題の MultiHead Latent Attention について説明します。上の図を見ると query の前と key-value の前に Latent という層が挟まっていて、RoRE を適用したものとしていないものを結合 (concat) するという形になっています。また、斜線が引かれている部分は推論時にキャッシュされます。

MLA は式で表すと添え字が多くてややこしいので、この図を見ながら理解することをお勧めします。特に RoPE の部分は考え方が特殊なので注意してください。

MLA の特徴

MLA は DeepSeek-V2^[2] で導入された方法です。一般に文章生成においては、途中まで生成された文章 (token 列) を入力として次の token を予測する、というタスクを繰り返します。前述のように、例えば以下の図では "a" まで入力して次の単語 "pen" を予測し、"pen" の次の単語を予測するときには下の入力の末尾に "pen" を加えてその次の単語を予測します。

$$\begin{CD} {\color{lightgray}これ} @. {\color{lightgray}は} @. {\color{lightgray}ペン} @. {\color{lightgray}です} @. {\color{lightgray}。} @. {\color{lightgray}[\textrm{delim}]} @. \textrm{this} @. \textrm{is} @. \textrm{a} @. {\color{red}?} \\ @AAA @AAA @AAA @AAA @AAA @AAA@AAA @AAA @AAA @AAA\\ [sos] @. これ @. は @. ペン @. です @. 。 @. [\textrm{delim}] @. \textrm{this} @. \textrm{is} @. \textrm{a} \end{CD}$$

Attention の計算において上の図の ? を予測するとき、"a" の位置に対応する出力の計算のためには、"a" の query と、"a" および "a" より前の token の key, value のみわかっていれば十分です。"a" より前の token の key, value は前の token の予測時に計算されているので、キャッシュすることで計算効率が向上します。これを KVcache といいます。しかし文章が長くなるとキャッシュに必要なメモリが多くなります。

KVcache の削減の試みは以前にもあったようですが、パフォーマンスが低下してしまうという問題がありました。MLA では cache するべき情報を低い次元のベクトル空間 (Latent Space) に埋め込むことで KVcache を削減し、かつパフォーマンスを維持することに成功しました。

MLA の仕組み

MLA は Multi-Head self-Attention をベースとしています。

MLA の入力を $(x_1, \cdots, x_L) \in (\mathbb{R}^{d_{emb}})^L$ とします。Head の数は $n_h$ とします。MLA については論文の図を見ながら式を見ることをお勧めします。

まず key と value については、線型写像

$$W^{DKV}: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d^{KV}_c}$$

により $x_\ell$ を $\mathbb{R}^{d^{KV}_c}$ (Latent Space) に埋め込んで、さらに RMSNormalization したものを

$$c^{KV}_\ell = \mathrm{RMS}(W^{DKV} x_\ell)$$

とおきます (論文には書いていませんが、コードを読む限り^[3]潜在空間への埋め込み時は RMSNormalization を行うようです)。

そして $c^{KV}_\ell$ を元に線型写像

$$\begin{align*}& W^{UK}_h: \mathbb{R}^{d^{KV}_c} \to \mathbb{R}^{d_q} \quad (1 \leq h \leq n_h) \\ & W^{UV}_h: \mathbb{R}^{d^{KV}_c} \to \mathbb{R}^{d_v} \quad (1 \leq h \leq n_h)\end{align*}$$

により

$$\begin{align*} k^c_{\ell,h} &= W^{UK}_h c^{KV}_\ell \quad (1 \leq h \leq n_h) \\ v^c_{\ell,h} &= W^{UV}_h c^{KV}_\ell \quad (1 \leq h \leq n_h) \end{align*}$$

と key, value を定めます。$c^{KV}_i$ は全ヘッド共通で、 推論時にキャッシュされます。$W_h^{DKV}$ の $D$ は down-projection の $D$, $W_h^{UK}$ の $U$ は up-projection の $U$ だと思われます。

query も線型写像

$$W^{DQ}: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d^{Q}_c}$$

により $x_\ell$ を Latent Space $\mathbb{R}^{d^{Q}_c}$ に埋め込んで、Normalization したものを

$$c^{Q}_\ell = \mathrm{RMS}(W^{DQ} x_\ell)$$

とおき、$c^{Q}_\ell$ を元に線型写像

$$W^{UQ}_h: \mathbb{R}^{d^{Q}_c} \to \mathbb{R}^{d_q} \quad (1 \leq h \leq n_h)$$

により

$$\begin{align} q^c_{\ell,h} = W^{UQ}_h c^Q_\ell \quad (1 \leq h \leq n_h)\end{align}$$

と query を定めます。

次に RoPE ですが、Attention の計算直前に $k^c_{\ell,h}$ に行列 $R_\ell$ を掛ける方式にすると、$k^c_{\ell,h}$ をキャッシュしていないので推論時に毎回 $R_\ell$ を掛ける必要があり効率が悪く、一方キャッシュされている $c^{KV}_\ell$ に $R_\ell$ を掛けると、query $q^c_{j ,h}$ との内積をとるときに

$${}^t (W^{UK} R_{\ell} c^{KV}_\ell) R_j q^c_{j ,h} = {}^t c^{KV}_\ell R_{-\ell} {}^t W^{UK} R_j q^c_{j ,h}$$

と、$R_{-\ell}$ と $R_{j}$ 間に行列 $W^{UK}_h$ が入ってしまい、相対位置がうまく表現されません。

そこで、RoPE を適用した query と key を別に用意し、さっき定義した $k^c_{i,h}$ や $q^c_{i,h}$ の後ろにくっつけます。RoPE を適用した key は推論時にキャッシュし、(おそらく) キャッシュ量の削減のため各ヘッドで共有します。具体的には以下の通りです。線型写像

$$\begin{align*} W^{KR} & : \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d_R} \\ W^{QR}_h & : \mathbb{R}^{d^{Q}_c} \to \mathbb{R}^{d_R} \quad (1 \leq h \leq n_h) \end{align*}$$

を用いて

$$\begin{align*} k^R_\ell &= R_\ell W^{KR} x_\ell \\ q^R_{\ell, h} &= R_\ell W^{QR}_h c^Q_\ell \\ k_{\ell, h} &= \mathrm{vconcat}(k^c_{\ell,h}, k^R_\ell) \\ q_{\ell, h} &= \mathrm{vconcat}(q^c_{\ell,h}, q^R_{\ell, h}) \\ \end{align*}$$

とします。ただし $\mathrm{vconcat}$ は縦方向 (token 列の方向ではなく、埋め込みベクトルの方向) に結合することを意味します。そして

$$\begin{align*} Q_h &= (q_{1, h}, \cdots, q_{n, h}) \\ K_h &= (k_{1, h}, \cdots, k_{n, h}) \\ V_h &= (v^c_{1, h}, \cdots, v^c_{n, h}) \end{align*}$$

として $h$ 番目の Head の Attention

$$o_{h} = \mathrm{Attention}(Q_h, K_h, V_h)$$

を計算して、$o_h$ を縦方向に結合して、線型写像 $W^O: \mathbb{R}^{d_v n_h} \to \mathbb{R}^{d_{emb}}$ を縦ベクトル毎に作用させて MLA の出力を得ます。

$$\begin{gather*} u_i = \mathrm{vconcat}(o_1, \cdots, o_{n_h}) \\ \mathrm{MLA}(x_1, \cdots, x_n) = (W^O u_1, \cdots, W^O u_n) \end{gather*}$$

DeepSeek-V3 の一番大きいモデル (671B) では

$$\begin{align*} d_{emb} &= 7168 && (\textrm{ 埋め込み次元 }) \\ n_h &= 128 && (\textrm{ Headの数})\\ d^{KV}_c &= 512 && (\textrm{ KVの潜在空間の次元}) \\ d^{Q}_c &= 1536 && (\textrm{ query の潜在空間の次元}) \\ d_q &= 128 && (\textrm{ RoPE を作用させないベクトルの次元}) \\ d_R &= 64 && (\textrm{ RoPE を作用させるベクトルの次元}) \\ \end{align*}$$

とされています。また、一番小さいモデルでは query の Latent Space は使われていません。

脚注

1. Jianlin Suほか. ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING.

2. DeepSeek-AI. DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model.

3. https://github.com/deepseek-ai/DeepSeek-V3