本記事では DeepSeek-V3 Technical Report の §2 の内容に沿って、DeepSeek-R1 (V3) で用いられているアーキテクチャの一つである、DeepSeep MoE (Mixture of Expert) について解説します。
この記事の内容は別の記事「DeepSeek-R1 (V3) のアーキテクチャ」から分岐したものです。基本的にはこの記事のみで完結するよう記述するつもりですが、tokenizer と token の埋め込みについて上記の記事を参照してください。
以下の図は DeepSeek-R1 (V3) の Transformer Block の全体像になります。赤枠で囲っている部分をこの記事で解説します。
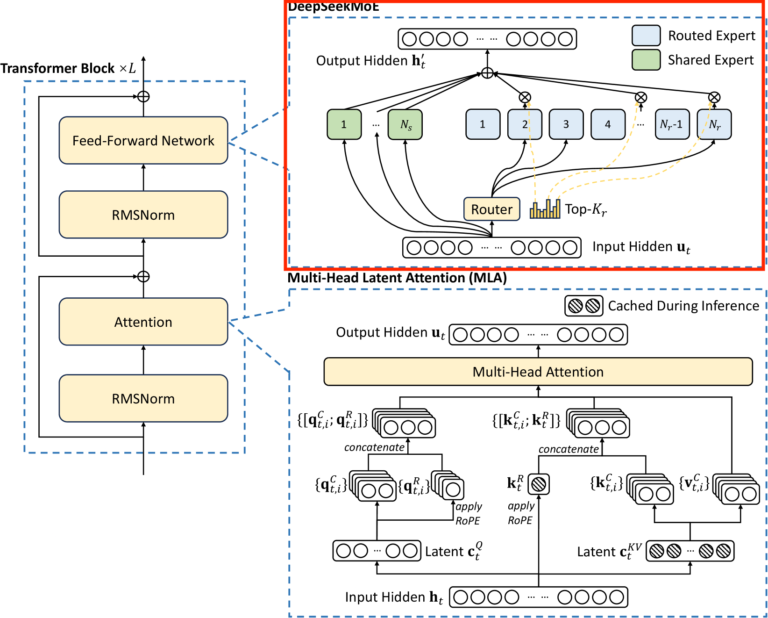
MoE とは？
通常の Transformer では通常、上の図の MoE に相当する部分において 1 つの 2 層の Feed-Forward Network
\mathrm{FNN}(x) = W_2 \varphi(W_1 x)
を用います。(\varphi は活性化関数です。バイアスがある場合もあります。)
MoE では \mathrm{FNN} を複数用意し、その中から入力に応じて処理する \mathrm{FNN} をいくつか選び、それらに処理をさせます。\mathrm{FNN} 達は専門家 (expert) に例えられ、専門家の集まりの中から適した専門家を選び、処理させる、と解釈できます。
MoE は \mathrm{FNN} の数を増やすことでモデルの表現力を高められ、縦にネットワークを積み上げるよりも学習効率、推論効率が良いというメリットがあります。
DeepSeek MoE とは
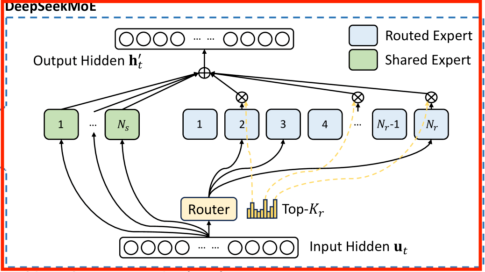
DeepSeekMoE の特徴のひとつ目は、普遍的な情報の処理を行う expert を備えていることです。つまり、どのような入力に対しても処理を行う expert (shared experts) がいくつか存在し、さらに入力に応じて他の expert を選択する、という仕組みになっています。
従来の MoE では shared experts が存在しないため、複数の expert が共通の知識を獲得しようとしてしまう懸念がありましたが、shared experts によって他の expert がより専門化され、その冗長性が解消されるという考えのようです。
DeepSeekMoE の特徴のふたつ目は、選択される expert の偏りの解消 (load balancing) の方法にあります。
一般に MoE の学習の際、特定の expert のみが選ばれてしまう問題が発生するようです。それを避けるために従来の方法では Auxiliary-Loss というものを導入し、学習の損失関数に加えていました。
しかし、Auxiliary-Loss が大きいとモデルの学習が妨げられパフォーマンスが低下し、小さいと特定の expert のみが選ばれる、という問題がありました。DeepSeekMoE では Auxiliary-Loss なし (Auxiliary-Loss-Free) にこの問題を解決しました。これにより上述の問題が解消されたようです。
正確には Auxiliary-Loss-Free な方法をメインとしつつ、1 つの入力列に対して expert が極端に偏ることを防ぐために、Auxiliary-Loss に非常に小さな係数をかけて損失関数に加えたようです。
DeepSeekMoE の入力と出力
ここからは DeepSeekMoE の具体的なアーキテクチャについて解説します。まずは DeepSeekMoE の入力から出力までの流れを説明します。
DeepSeekMoE は各 token の位置毎に計算され、パラメータは各位置で共通のものを用います。入力データを x \in \mathbb{R}^{d_{emb}} とおきます。d_{emb} は埋め込みベクトルの次元です。
Expert の形と、各 Expert への振り分け (routing) に分けて説明します。
Expert について
各 Expert は2 層の Feed-Forward Network
\mathrm{FNN}_i(x) = W^2_i \varphi(W^1_i x)
で与えられ、これを N_s + N_r 個用意します。ただし \varphi は活性化関数で、ベクトルの要素毎に適用されます。DeepSeek-V3 では
\varphi(x) = \mathrm{silu}(x) = x \cdot \frac{1}{1 +e^{-x}}
が用いられています。W^1_i: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{d_1}, W^2_i: \mathbb{R}^{d_1} \to \mathbb{R}^{d_{emb}} は線型写像です。(DeepSeek-V3 のコードでは W^1_i と同じを形の行列 W^3_i も定義し、W^1_i x の代わりに要素毎の積 W^1_i x \cdot W^3_i x を使っていますが理由は分かりません。)
1 \leq i \leq N_s のとき
\mathrm{FNN}^{(s)}_i = \mathrm{FNN}_i
を shared expert、N_s + 1 \leq i \leq N_r のとき
\mathrm{FNN}^{(r)}_{i-N_s} = \mathrm{FNN}_i
を routed expert と呼びます。つまり最初の N_s 個を shared expert、残りの N_r を routed expert とし、routed expert の添字を 1 から振り直します。
routing の仕組み
次に N_r 個の routed experts から K_r 個の expert を選択する方法を説明します。まず線型写像 W^G: \mathbb{R}^{d_{emb}} \to \mathbb{R}^{N_r} をとり、W^G x の各成分の sigmoid を取ります。
\begin{pmatrix}s_1 \\ \vdots \\ s_{N_r} \end{pmatrix} = \mathrm{sigmoid}(W^G x)
s_i を i 番目の expert のスコアと呼びます。DeepSeek-V2 では softmaxを取っていましたが、V3 では sigmoid にしたようです。ちなみに論文では 「i 番目の expert の centroid ベクトル e_i との内積をとる」と書いていますが、行列 W^G の i 行目が e_i です。
して s_1, \cdots s_{N_r} のうち、値が大きいもの上位 K_r 個の添字の集合を
\mathrm{Topk}((s_1, \cdots, s_{N_r}), K_r)
とおき、
\begin{align*}
g_i^{\prime} &= \begin{cases} s_i & (i \in \mathrm{Topk}((s_1, \cdots, s_{N_r}), K_r)) \\ 0 & (それ以外) \end{cases} \\
g_i &= \frac{g_i^{\prime}}{\sum_{j=1}^{N_r} g_j^{\prime}}
\end{align*}
とします。つまり、\mathrm{Topk} に含まれないものは 0 とし、和が 1 になるように正規化します。入力 x から (g_1, \cdots, g_{N_r}) を得る処理を
\mathrm{Gate}(x) = (g_1, \cdots, g_{N_r})
とおきます。W^G の G は Gate の G です。
そして MoE の出力を
\mathrm{MoE}(x) = \sum_{i=1}^{N_s} \mathrm{FFN}^{(s)}_i (x) + \sum_{i=1}^{N_r} g_i \mathrm{FFN}^{(r)}_i (x)
とします。
DeepSeek V3 の一番大きいモデル (671B) では
\begin{align*}
N_s &= 1 && (\textrm{shared expert の数})\\
N_r &= 256 && (\textrm{routed expert の数})\\
K_r &= 8 && (\textrm{選ばれる expert の数})\\
d_1 &= 2048 && (\textrm{FNN の中間層の次元})\\
\end{align*}
とされています。
コード上では、routed expert をいくつかのグループに分け、グループを選んでからその中の expert を選ぶ処理になっています。また、61 個あるうちの最初の 3 つの Transformer Block では MoE の代わりに普通の \mathrm{FFN} が使われています。
Load Balancing について
次は expert の偏りの解消について説明します。まずは従来の方法で用いられていた Auxiliary-Loss について説明します。
Auxiliary-Loss とは
ネットワークに L 個の token が入力されたとし、MoE 層への L 個の入力を (x_1, \cdots, x_L) \in (\mathbb{R}^{d_{emb}})^n とおきます。入力の \ell 番目のベクトル x_{\ell} に対してスコアを
\begin{pmatrix}s_{\ell, 1} \\ \vdots \\ s_{\ell, N_r} \end{pmatrix} = \mathrm{sigmoid}(W^G x_{\ell})
とおきます。そして i 番目の expert が選ばれた入力の位置の集合を
C_i = \{\ell \mid 1 \leq \ell \leq L, \ i \in \mathrm{Topk}((s_{\ell, 1}, \cdots, s_{\ell, N_r}), K_r)\}
とおき
\begin{align*}
f_i &= \frac{N_r}{K_r} \frac{|C_i|}{L} \\
s^{\prime}_{\ell, i} &= \frac{s_{\ell, i}}{\sum_{j=1}^{N_r} s_{\ell, j}} \\
P_i &= \frac{1}{T} \sum_{\ell = 1}^L s^{\prime}_{\ell, i}
\end{align*}
とします。f_i は i 番目の expert が選ばれた割合に \frac{N_r}{K_r} を掛けたもので、P_i は i 番目の expert のスコア (を正規化したもの) の平均です。softmax でスコアを計算する場合は正規化が必要ありませんが、V3 では sigmoid を使っているので正規化しているものと思われます。f_i に掛けられている \frac{N_r}{K_r} については掛けられている理由がわかりません。
そして、Auxiliary-Loss \mathcal{L}_{Balance} を
\mathcal{L}_{Balance} = \alpha \sum_{t=1}^T f_i P_i
と定めます。\alpha はハイパーパラメータで、DeepSeek-V3 では非常に小さな値に設定されたようです。\mathcal{L}_{Balance} は expert の振り分け方が偏るほど大きくなるようですが、詳細は省略します。
Auxiliary-Loss-Free な Load Balancing
DeepSeek ではもっと単純に偏りの解消を実装しました。学習中に Expert が選択される回数を監視し、選択される回数が少ない場合はスコアに大きめバイアスを加え、多い場合はバイアスを小さくするという方法です。ただしバイアスは \mathrm{Topk} の計算にのみ使用され、最終的な出力には使用されません。
バイアスは学習のバッチ毎に更新され、以下のように更新されるようです。
-
b_i (1 \leq i \leq N_r) の初期値を 0 とする.
-
バッチ内で i 番目の Expert が選ばれた回数 c_i を計算する.
-
\bar{c} を N_r / (バッチ内の token 数) とし、e_i = c_i -\bar{c} を計算する.
-
b_i \leftarrow b_i + u \cdot \mathrm{sign}(e_i) と更新する. ただし u > 0 はハイパーパラメータ.
つまり、平均より多く選ばれたものはバイアスを u 減らし、平均より少なく選ばれたものはバイアスを u 増やします。ちょうど平均だった場合はそのままです。
以上が DeepSeekMoE の仕組みです。
Discussion