👻

Rユーザのための0から始めるJulia入門

2024/03/07に公開

2件

Julia

tech

本記事について

2024/3/9に開催された某研究会での発表資料。「90分で入門・前処理についてレクチャーする」というなかなかのハードスケジュールなので、必要最小限の内容にとどめている。

本記事では「入門」部分のみ紹介。前処理については以下の記事を参照。

なおJuliaの環境構築は終了していることを想定。

加筆修正について（2024/3/8）

本記事公開後に識者の方からコメントをいただき、初稿の誤りやより効率的な書き方について教示いただきました。特に配列とベクトルの定義については筆者の誤解があったため、修正しています。

変数の作成

スカラー／文字列

代入演算子は=。Rと同様に、変数の宣言時に型を指定する必要はない。

x = 10
y = 2.0
z = x * y
msg = "xとyを掛けた結果は、"
println(msg, z)

上記のコードを実行すると、「xとyを掛けた結果は、20.0」と表示されるはずだ。このコードと出力は、Rユーザからすると慣れないところだろう。各変数の型を確認してみよう。

using DataFrames # 後述する、DataFramesパッケージを使用
df = DataFrame(x = x, y = y, z = z, msg = msg) # データフレームを作成。データフレームについては後述するが、Rのクラスをイメージすればよい

Rでは、変数に代入する値が整数でも実数でも、原則的に変数はnumericという同じ型になるが、Juliaでは上記のように整数（Int）と実数（より正確には浮動小数点数型Float）が区別される。

またRでは、これらを掛算した結果（x * y）は「20」と出力されるが、Juliaでは「20.0」になることに注意されたい（いわゆる暗黙の型変換）。

（多次元）配列

ベクトル・行列の作成

参考：Juliaの行列・ベクトルを完全に理解すっぞ！！

配列の作成には[]を用いるが、以下の点に注意。

縦ベクトル：各要素を,で区切る（例：a = [1, 2, 3]）
行数1の2次元配列（行列)：各要素をスペースで区切る（例：a = [1 2 3]）
- 横ベクトルではないことに注意

a = [10, 11, 12] # 縦ベクトルの作成
size(a) # 次元を返す関数。(3,)と表示される。

b = [10 11 12] # 行数1の2次元配列の作成
size(b) # 次元を返す関数。(1, 3)と表示される。

ベクトルや配列の要素にアクセスするには、Rと同様に「1」から始まるインデックスを指定すればよい。

a[2] # 縦ベクトルの2番目の要素である、11が出力される

b[1, 2] #　1行3列の行列の、1行2列目の要素である、11が出力される

2×3のような、複数の行数と列数を持つ行列を作成するには様々な方法がある。例えば行数1の配列をコロン（;）で繋いだり、改行したりして、以下のように行列を定義できる。

# いずれも、
# 1 2 3
# 4 5 6
# という行列ができる

[1 2 3; 4 5 6]

[1 2 3
 4 5 6]

ただRに慣れた身としては、要素をカンマで区切りたいので、縦ベクトルを水平方向に連結するほうが好みではある。

hcat([1, 4], [2, 5], [3, 6])

追記あり

コメント欄で例示いただいたように、;や;;を用いて、記号[]を用いずとも効率的に行列を作成できるらしい。

[1; 4;; 2; 5;; 3; 6] # hcat([1, 4], [2, 5], [3, 6])と同じ出力が得られる

行列に対して、「特定の行（または列）のみ」参照するには、以下のようにコロン:を使う。Rでは空白で良かった部分にコロン:を埋める、と覚えればよい。

mat = hcat([1, 4], [2, 5], [3, 6])
mat[1, :] # 1行目だけを参照
mat[:, 2] # 2列目だけを参照
mat[:, 1:2] # 1～2列目だけを参照
mat[:, [1, 3]] # 1, 3列目だけを参照

規則的な要素を持つベクトルの作成

例えばa = [0, 0, 0, 0, 0]やb = [1, 2, 1, 2]のように、規則的な要素を持つベクトルを作成したいことがある。Rでこれらのベクトルを作成するにはrep()を使うが、Juliaでは以下のような関数を利用できる。

まず、要素が全て0または1のベクトルは、それぞれzeros()やones()で容易に作成できる。

zeros(3) # [0.0, 0.0, 0.0]が作成される（縦ベクトル）

ones(5) # [1.0, 1.0, 1.0, 1.0, 1.0]が作成される（縦ベクトル）

では要素が全て2の場合はtwos()か...というとそういう関数はないので、一般化された方法としてはfill()を使う。第一引数に初期化する要素を、第二引数以降に配列の次元数を指定する。

fill(2, 3) # 要素が全て2で、要素数が3の縦ベクトル

fill(2, 3, 2) # 要素が全て2で、3行2列の行列

b = [1, 2, 1, 2]のように周期的なベクトルは、repeat()を使うとよい。第一引数に複製する要素を、第二引数以降は、引数innerとouterを使い分ける。

repeat([1], 3) # [1, 1, 1]という縦ベクトル。第一引数は、要素数1の配列とすることに注意

repeat([1, 2], inner = 2) # [1, 1, 2, 2] という縦ベクトル

repeat([1, 2], outer = 2) # [1, 2, 1, 2] という縦ベクトル

等差数列を作成するには、Rではseq()を用いるが、Juliaではcollect()を用いる。なおRではseq(from = xxx, to = xxx, by = xxx)という引数の順番だが、Juliaで等差数列を作成する際はコロンを用いて、初項:公差:末項と書くことに注意。公差が1でよいなら省略可能。

collect(1:2:10) # [1, 3, 5, 7, 9]という縦ベクトル

なお詳しくはNumpyとの比較で学ぶJuliaのベクトル・行列の記法を参照してもらいたいが、実はcollect()は不要で、しかも不要の場合の方が処理が早いらしい。

a = 1:2:10
a

上記のコードを実行すると1:2:9とだけ表示されるので、果たして本当に等差数列が作成されているのかと不安になるところだが、forループ（後述）で要素を一つずつ表示させてみると、確かに問題なく配列が定義されている。

a = 1:2:10
for i in 1:5
    println(a[i])
end

データフレームの作成

Rと同様に、Juliaでもデータフレームを定義すると便利なことが色々とある。Juliaではデータフレームを作成するには、DataFrames.jlというパッケージの、DataFrame()という関数を必要とする。

なおここでついでに、パッケージについても説明しておこう。

パッケージのインストールとロード

Juliaでは、パッケージをインストールするためのパッケージマネージャPkgを使う（参考）。

まずはusing Pkgでパッケージマネージャを起動する。

using Pkg

なおimportで読み込む方法もあるが、これらの違いは下図を比較すると分かりやすい。要するにimportだとパッケージ名の修飾が必要だが、usingだと修飾を省略できる、ということ（とはいえ実はもうちょっと話は複雑で、公式ドキュメントの「モジュール」の説明などを参照されたい）。

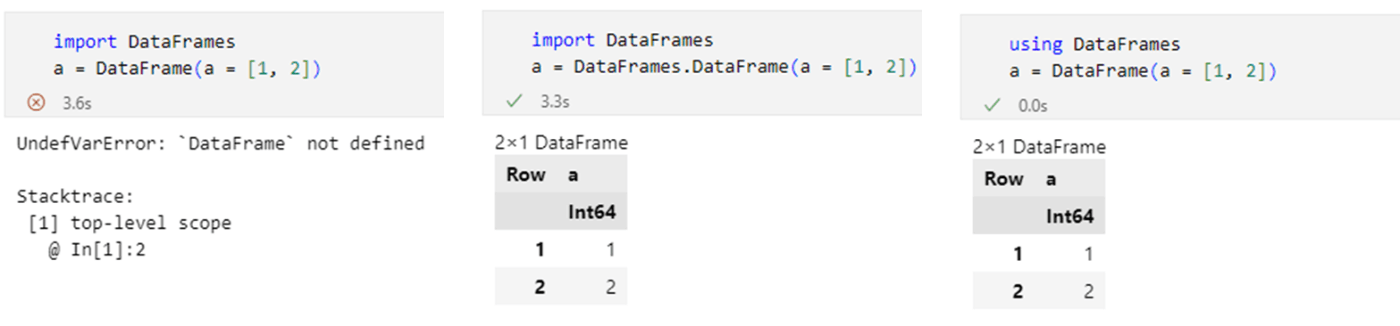
話を戻そう。パッケージをインストールするには、Pkg.add()を用いる。ここでDataFrames.jlをインストールしても良いのだが、研究会参加者は後々TidierData.jlパッケージを使うので、ここでインストールしてしまおう。

TidierData.jlパッケージは、DataFrames.jlや、パイプライン処理を実現するためのChain.jlのラッパーなので、TidierData.jlをロードしさえすれば、自動的にDataFrames.jlやChain.jlもロードしたことになる。

TidierData.jlのインストールが終わったら、ロードもしてみよう。

Pkg.add("TidierData") # 末尾に`.jl`は付けなくてよい。なお時間がかかる
using TidierData

データフレームの作成と参照

ここからが本題。using TidierDataを実行しているなら、以下のようにデータフレームを作成できる。この記法はRのdata.frame()と同様。

using TidierData
df = DataFrame(a = [1, 2],
               b = ["a", "b"])

df

データフレーム内の特定の列を参照する場合は、以下のように、変数名.列名と書く。これはRで言うところのdf$aに相当する。

df.a # データフレームdfの、aという名前の列を参照

ちなみに行列をデータフレームに変換するには、以下のようにすればよい。

mat = fill(0, 3, 3) # 要素が全て0の、3×3行列
DataFrame(mat, :auto) # Rで言うところの、as.data.frame(mat)と同じ

値渡しとポインタ渡し

このあたりはポインタなどが関係してくるので非常にややこしいのだが、Juliaでは「あるオブジェクトを複製したい」場合、Rと同様に代入演算子=を用いて以下のように書くことは避けたほうが良い。以下のコードを実行すると、操作をしていないはずのbまでも要素が変わっている。

a = [1, 2]
b = a # 注目

a[1] = 100 # aの1つ目の要素だけを置換
b # [100, 2]が出力される

これはデータフレームでも同様である。

using TidierData
df = DataFrame(a = [1, 2],
               b = ["a", "b"])

df2 = df # 注目
df.a = [10, 20]

df2 # df2.aも変わっている

代入演算子を用いた方法は、ある変数aを、別の名前で呼ぶことも可能にしたというような処理を指す。東方仗助に対して「これからてめーをジョジョって呼んでやるぜ！」と言っているようなものである（ジョジョ = 東方仗助）。

この問題に対応するには、copy()を使うとよい。

a = [1, 2]
b = copy(a) # 注目

a[1] = 100 # aの1つ目の要素だけを置換
b # [1, 2]が出力される

外部ファイルの読み込み

`CSV`パッケージ（文字コード：UTF-8）

以下のような.csvファイルを読み込みたいとしよう（ファイル名はjulia_read_utf8.csv）。ポイントは、マルチバイト文字（ここでは日本語）が存在し、文字コードUTF-8で保存されていることだ。

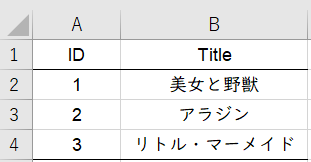
この場合、CSV.jlパッケージのFile()を用いて問題なく読み込める。以下のコードでは、読み込んだファイルをデータフレームに変換している。

using Pkg
Pkg.add("CSV")

using CSV, TidierData
df_csv = DataFrame(CSV.File("julia_read_utf8.csv"))

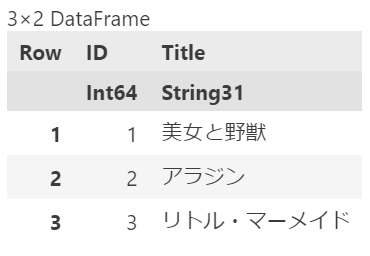
`CSV`パッケージ（文字コード：Shift_JIS）

同じcsvファイルが、文字コードShift_JISで保存されているとしよう。この場合、同じコードを実行すると以下のように日本語がうまく表示されない。

その場合、以下の記事を参考にStringEncodings.jlパッケージを使うとよい。

[Julia] StringEncodings パッケージ - ShiftJIS のCSVファイルとも仲良しになろう

Julia de 線形代数

$\bm{y} = \alpha + \beta \bm{x}$ の、単回帰分析の文脈で説明しよう。なお簡単のため残差は全て0とする。スカラー $\alpha, \beta$ と、縦ベクトル $\bm{x}$ がすでに以下のように与えられているとする。これらを用いて、縦ベクトル $\bm{y}$ を作りたい。

α = 1 # Juliaでは \alpha と入力した後でtabを押すとギリシャ文字に変換される
β = 2
x = [1, 4, 9]

まずは $\beta \bm{x}$ を計算してみる。縦ベクトルの全ての要素を定数倍する演算は認められているので、以下のように書ける。

β * x # [2, 8, 18]が出力される

では次に、切片 $\alpha$ を足してみよう。ここで注意が必要なのは、Rと違って、「スカラー + ベクトル」の計算はできないことだ（Rではスカラーは長さ1のベクトルであり、ベクトルのリサイクルが行われる関係で、これが可能になっている）。以下のコードはエラーが出る。

α + β * x # エラーになる

ここで実行したい処理は、beta * xという縦ベクトルの各要素に対して、定数（alpha）を足す、ということだ。このように、エレメントワイズで演算を行いたいとき、演算子に.を付けることに注意してほしい。

α .+ β * x # [3, 9, 19]が出力される

もちろん他の演算子でも同様だ。例えばxの各要素を2乗したいときは、演算子を.^にしなければならない。

x.^2 # [1, 16, 81]が出力される

関数の場合は、関数名の直後に.を付ける。

sqrt.(x) # [1.0, 2.0, 3.0]が出力される

要素数が等しい2つの縦ベクトルがあるとき、同じ位置の要素同士の足し算／引き算は可能。

a = [1, 2, 3]
b = [10, 20, 30]
a + b # [11, 22, 33]が出力される。

しかし同じ位置の要素同士の掛け算／割り算を行うには、.*や./を用いる必要がある。共分散や相関係数を求めるときには途中でこの計算が発生するので、注意しよう。

a = [1, 2, 3]
b = [10, 20, 30]
a .* b # [10, 40, 90]が出力される。

以下のコードでは、いわゆる行列の積の計算を行っている。

a = [1, 2, 3]
b = transpose([10, 20, 30]) # transpose()で、縦ベクトルを、1行3列の行列に転置
a * b

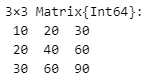
反復処理

forループ

Juliaにおけるforループの記法は、Rと非常に似ている。{}で処理の範囲を囲む代わりに、for ~ endで処理の範囲を指定する。前述のコードを再掲する。

a = 1:2:10 # [1, 3, 5, 7, 9]という縦ベクトル
for i in 1:5
    println(a[i])
end

上記のコードでは、ベクトルaの要素数が5ということを知ったうえでfor i in 1:5と書いたが、もちろんここは要素数を関数によって取得したうえで書くこともできる。Rと同じく、ベクトルの要素数を取得する関数はlength()だ。

a = 1:2:10 # [1, 3, 5, 7, 9]という縦ベクトル
for i in 1:length(a)
    println(a[i])
end

なおやはりRと同様に、for i in 1:5というのはfor i in [1, 2, 3, 4, 5]と同義なのだから、これは単に5回ループせよと命令しているのではなく、「iを1, 2, 3, 4, 5と更新しなさい」という処理を表している。

よって以下のように書くと、5番目の要素と1番目の要素が順に取り出される。

a = 1:2:10 # [1, 3, 5, 7, 9]という縦ベクトル
for i in [5, 1]
    println(a[i])
end

while文

「条件が満たされる限り処理を繰り返す」while構文では、反復処理を指せる範囲をwhile~endで囲む。以下のコードは

cnt = 0 # 初期値
while cnt <= 5
    println("count:", cnt)
    cnt += 1 # count = count + 1と同じ
end

複数の条件を「かつ（&&）」もしくは「または（||）」で結合させることもできる。

df = DataFrame(
    a = [1, 2, 5, 10, 15],
    b = [1, 5, 10, 20, 30]
)

i = 1
a = df.a[i]
b = df.b[i]

while a <= 10 && b <= 10
    println("[a, b] = [$a, $b]")
    i += 1
    a = df.a[i]
    b = df.b[i]
end

df = DataFrame(
    a = [1, 2, 5, 10, 15],
    b = [1, 5, 10, 20, 30]
)

i = 1
a = df.a[i]
b = df.b[i]

while a <= 10 || b <= 10
    println("[a, b] = [$a, $b]") # $を付けることで、文字列内でオブジェクトを参照できる
    i += 1
    a = df.a[i]
    b = df.b[i]
end

条件分岐

Juliaにおける条件分岐の記法も、やはりRに似ている。

a = 1:2:10 # [1, 3, 5, 7, 9]という縦ベクトル

for i in 1:length(a)

    if mod(a[i], 3) == 0
        println("3の倍数")
    elseif mod(a[i], 5) == 0
        println("5の倍数")
    else
        println(a[i])
    end
    
end

ちなみに、C言語にあるような、switch/case記法による条件分岐はJulia実装されていないらしい。

自作関数の定義

Rと同様に、functionを用いる。試しに内積を返す関数を計算してみよう（実践的にはLinearAlgebra.jlパッケージのdot()を使用してもよい）。

a = [1, 2, 5, 2, 3]
b = [1, 1, 2, 2, 3]

function my_dot(a, b)
    dot = sum(a .* b) # 内積の計算
    return dot # 戻り値
end

my_dot(a, b)

ちなみに内積を求めるなら、一つ目の縦ベクトルを転置させ、「1行5列の行列 × 5行1列の行列の積」として計算してもよい。

a = [1, 2, 5, 2, 3]
b = [1, 1, 2, 2, 3]

transpose(a) * b

演算子'で簡単に転置させることもできるので、以下のように簡潔に内積を求められる。

a = [1, 2, 5, 2, 3]
b = [1, 1, 2, 2, 3]

a' * b

パイプライン処理

base pipe

Juliaにはデフォルトで、R version 4.1.0以降のようなパイプ演算子|>がある。ただしRのnative pipeと違い、パイプ演算子の後に書く関数には()を付けない。

[1, 2] |> length # length([1, 2])と同じ

ただしプレースホルダーを使うことができない。プレースホルダーを使うには、様々なパッケージを用いる必要がある。恐らくデファクトスタンダードはChain.jlパッケージを用いることだ。これにより、複数のパイプライン処理も効率的に書ける。

なおTidierData.jlパッケージはChain.jlのラッパーなので、TidierData.jlを読み込めば自動的にChain.jlを用いたパイプライン処理が可能になる。

`Chain.jl`を用いたパイプライン処理

詳しくは公式ドキュメントを見てもうらうとして、ここでは簡単に説明する。

まず、オブジェクトを渡す関数が1つだけなら、以下のように書く。@chainマクロのあとに、パイプライン処理で渡されるオブジェクトと、渡す関数を順に書く。プレースホルダーは_。

using TidierData
a = 3
b = @chain a mod(5, _) # mod(5, a)と同じ
b

もし複数の関数にオブジェクトを渡すパイプライン処理を行うなら、以下のようにbegin～endの範囲内に書く。

using TidierData
a = 3
b = @chain a begin
    mod(5, _)
    length
end
b

RとJuliaの間でオブジェクトを渡し合う

これを言ってしまうと、「えっ、じゃあ（速度が問題にならない）ほとんどの処理はRコード化すればよくない...？」となってしまうのだが、まあそこは目をつむることにしよう。

まず前提として、RがPCにインストールされており、RCall.jlパッケージJuliaにインストールされている必要がある。以下の解説では、これらの環境設定は終わっているものとする。

以下のコードを実行してみよう。まずJulia上でオブジェクトaとbを作成している。aはスカラー、bは縦ベクトルなので、前述のようにJuliaではa + bという演算はできない。

しかし以下のコードでは、R"hogehoge"という記法により、二重引用符（""）内でRコードを書ける。もしRコード内に二重引用符が発生するなら、エスケープシーケンスする。

R"print(\"hello world\")"

なおRコード内でJulia環境のオブジェクトを参照する場合は、オブジェクト名に$を付ける必要があることに注意。

using RCall
a = 1
b = [1, 2, 3]
R"$a + $b"

あるいは、@rputマクロにより、Julia上で作成したオブジェクトを、R環境に渡すことができる。

using RCall
c = 10
d = [10, 20, 30]

@rput c
@rput d
R"c + d"

Rコードにより行われた結果をJulia側に出力するには、rcopy()を使う。

out = rcopy(R"c + d")
println(out) # [20, 30, 40]が出力される

ただしこの方法では、Rコード内で作成されたオブジェクトは取り出すことができない。

out = rcopy(R"tmp = c + d")
println(tmp) # エラー
println(out) # [20, 30, 40]が出力される

Rコード内で作成したRオブジェクトを、Julia環境に渡すには、@rgetマクロを使う。

R"out = c + d"
@rget out
println(out)

この記法を使えば、Rのtidyverseを用いた高度な処理や可視化もJulia上で実現できる。仮に、Rにtidyverseパッケージがインストール済みであるなら、Juliaからggplot2で作図ができる。

using Random, RCall, TidierData

Random.seed!(123) # Random.seed!()で乱数のシードを指定
df = DataFrame(x = rand(20)) # rand()は、0~1の連続一様乱数を、任意の個数、縦ベクトルとして生成する関数
@rput df

R"
library(tidyverse)

ggplot(data = df, mapping = aes(x = x)) +
   geom_histogram()
"

あくまで私見だが、RとJuliaを使い分けるつもりのユーザは、Juliaにおける可視化は、上記のようにRのggplot2を呼ぶのが最も楽ではないかと思う。Rの可視化機能は（base plotであっても）高機能なので。

ggplot2をJuliaに移植した、TidierPlots.jlというJuliaパッケージもあるのだが、これを使うくらいなら、素直にRを呼んだほうがよい気がする。

とはいえそれは、あくまで自分一人でスクリプトが完結する場合の話。もし他者とコードを共有する場合（例えば論文のSupplementary materialとして公開）、多くのパッケージを必要としたり、パッケージのバージョンによる挙動の違いが顕著だったり、複数の言語をインストールする必要があったりすると、処理の再現可能性が低下する。

そういう意味では、Juliaで可視化するなら素直にPlots.jlパッケージを使ったほうがいいかもしれないし、前処理もこの後説明するようにTidierData.jlのような規模の大きなパッケージではなく、DataFrames.jlの関数を覚えたほうが良いかもしれない。

卒業試験

ここまで学んだ技術を使って、Juliaで中心極限定理のシミュレーションをしてみよう。

使用するパッケージ
- TidierData.jl
母集団分布
- 0~1の連続一様分布
- ということは母平均は0.5
サンプルサイズ
- 最初に一度だけ、0~1の連続一様分布に従う乱数を1つ生成し、以下の条件によってサンプルサイズを決定する
  - 0.25未満なら998
  - 0.5未満なら999
  - 0.75未満なら1000
  - 1.0未満なら1001
乱数のシード
- Random.jlパッケージ（標準パッケージ）のRandom.seed!()を用いて、乱数のシードを指定しておく（例：Random.seed!(123)）
推定量
- 標本平均
- なお算術平均の計算には、自作関数を使用すること（自作関数内部で使ってよい既存関数は、合計を求める関数sum()のみ）
  - 実はTidierData.jlパッケージをインストール済みなら、Statistics.jlパッケージも内包されているので、using Statisticsを実行すれば、直接的に算術平均を返す関数mean()を使用できる
  - ここではあくまで実習のため関数を自作する
イテレーション数（標本平均を得る回数）
- 500,000
結果の確認方法
- 「イテレーション数ぶんの標本平均」のヒストグラムを描画する
  - JuliaのPlot.jlを使っても、RCall.jlでRの可視化関数を用いてもよい

Discussion

antimon2

いくつか指摘したい点があるのですが、そこそこ重要な所を取り急ぎコメントしておきます。

（多次元）配列

…

横ベクトル：各要素をスペースで区切る（例：a = [1 2 3]）

これは正確には横ベクトルではありません。2次元配列（1行3列の行列）になります。
明示的に横ベクトルを直接書く方法はありませんが、よく書く方法としては a = [1, 2, 3]' または a = transpose([1, 2, 3]) となります。これらは特別な型になりますが行列（2次元配列）にはなりません。（なお前者は a = adjoint([1, 2, 3]) と同じ意味になり、要素が複素数の場合は共役複素数になってしまうので注意が必要ですが、（数学的に言う）実数の範囲では転置と変わらないので記述が短いのでよく使われます）

なお1行N列の行列と横ベクトルの違いは、縦ベクトルとの積を実行すると分かります。

julia> a1 = [1, 2, 3]'  # 横ベクトル
1×3 adjoint(::Vector{Int64}) with eltype Int64:
 1  2  3

julia> a2 = [1 2 3]  # 1行3列の行列
1×3 Matrix{Int64}:
 1  2  3

julia> b = [1, 3, 5]  # 縦ベクトル
3-element Vector{Int64}:
 1
 3
 5

julia> a1 * b  # 結果はスカラーになる
22

julia> a2 * b  # 結果は要素数1の配列（ベクトル）になる
1-element Vector{Int64}:
 22

おまけ。

ただRに慣れた身としては、要素をカンマで区切りたいので、縦ベクトルを水平方向に連結するほうが好みではある。

そこを敢えて Julia の良さをアピールさせていただくと、Julia で多次元配列は ; を駆使して [] のネストを少なくコンパクトに（場合によっては直感的に）書けます。
例えば記載の例 hcat([1, 4], [2, 5], [3, 6]) は以下のように書くことができます。3次元以上の多次元配列も同様です、その例も合わせて。

julia> [1; 4;; 2; 5;; 3; 6]  # `[1 2 3; 4 5 6]` と同等
2×3 Matrix{Int64}:
 1  2  3
 4  5  6

julia> [1 2
        3 4
        ;;;
        5 6
        7 8]
2×2×2 Array{Int64, 3}:
[:, :, 1] =
 1  2
 3  4

[:, :, 2] =
 5  6
 7  8

さらについでに。先ほどは「1行N列の行列は横ベクトルではない」と話しましたが、逆に「縦ベクトルではなくM行1列の行列を記述したい」という要望があったら、以下のように書く必要があります。

julia> [1;2;3;;]  # こう書けば3行1列の行列になる
3×1 Matrix{Int64}:
 1
 2
 3

julia> [1;2;3]  # これだと縦ベクトルになってしまう
3-element Vector{Int64}:
 1
 2
 3

以上、参考までに。

das Kino

コメントありがとうございます！！　勉強中のため、まず記事を書いてみて詳しい方にコメントをいただきながら都度修正していこうと思っていましたが、さっそくこんなに詳しくご指摘いただけてたいへんありがたいです。整理しながらご指摘反映させたいと思います。

本記事について

加筆修正について（2024/3/8）

変数の作成

スカラー／文字列

（多次元）配列

ベクトル・行列の作成

規則的な要素を持つベクトルの作成

データフレームの作成

パッケージのインストールとロード

データフレームの作成と参照

値渡しとポインタ渡し

外部ファイルの読み込み

CSVパッケージ（文字コード：UTF-8）

CSVパッケージ（文字コード：Shift_JIS）

Julia de 線形代数

反復処理

forループ

while文

条件分岐

自作関数の定義

パイプライン処理

base pipe

Chain.jlを用いたパイプライン処理

RとJuliaの間でオブジェクトを渡し合う

卒業試験

Discussion

（多次元）配列

`CSV`パッケージ（文字コード：UTF-8）

`CSV`パッケージ（文字コード：Shift_JIS）

`Chain.jl`を用いたパイプライン処理