Rust で自動微分ライブラリ作ってみた

次回 -> 応用編

前回は Rust でディープラーニングフレームワークを作ってみましたが、バックプロパゲーションに必要な微分の計算は手でやっていました。これを自動化できないかというのが今回のお題です。

業界では自動微分(autograd)と言われる技術で、 PyTorch や TensorFlow では標準装備されているみたいです。

自動微分ってなんだか難しそう……と思っていましたが、とある動画でそれほど難しくなさそうに思えたので自前で実装してみました。

例によってコードは下記にあります。

https://github.com/msakuta/rustograd

自動微分でできること

まず断っておくべきこととして、ここでいう自動微分とは Python における sympy や Matlab の Symbolic math toolbox や Maxima や Wolfram Alpha のようなシンボリックな微分ではなく、数値が分かっている変数間の微分係数を求めることを指します。ニューラルネットワークにおいては重み係数に関する微分係数を大量に計算するので、このようなものが必要とされます。

[2023/7/26追記] また、ここで作るのは式を構築してから評価する Define and Run という設計のライブラリで、別の設計指針で Define by Run と呼ばれるものは式の構築と評価を1パスで行います。

まずは変数を定義する必要があります。 Term::new で次のように a, b, c といった変数を定義し、それに対して演算していきます。

use rustograd::Term;

let a = Term::new("a", 123.);
let b = Term::new("b", 321.);
let c = Term::new("c", 42.);
let ab = &a + &b;
let abc = &ab * &c;

Rust の所有権の扱いの都合上、 a + b というふうには書けず、 &a + &b のように参照を付ける必要があります。この不便は後ほどマクロで改善します。

一通り変数と演算の定義が終わったら、 derive メソッドを使って偏微分係数を計算することができます。

let abc_a = abc.derive(&a);
println!("d((a + b) * c) / da = {}", abc_a); // 42
let abc_b = abc.derive(&b);
println!("d((a + b) * c) / db = {}", abc_b); // 42
let abc_c = abc.derive(&c);
println!("d((a + b) * c) / dc = {}", abc_c); // 444

一つ一つの変数に対する偏微分係数を求めても良いのですが、式が複雑になってくるとバックプロパゲーションを使って一度に計算した方が高速です^[1]。このためには backprop() メソッドが使えます。

abc.backprop();

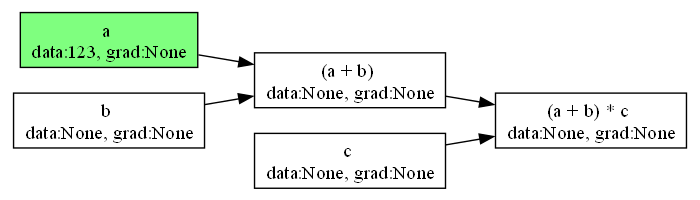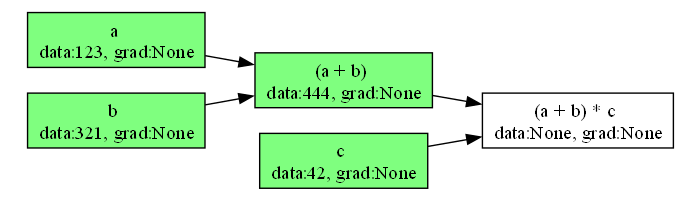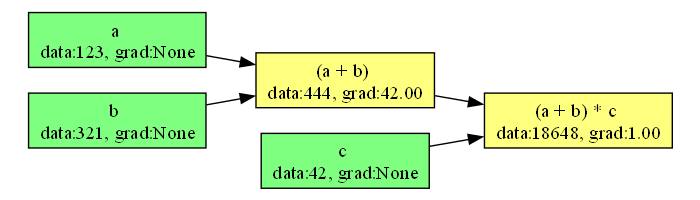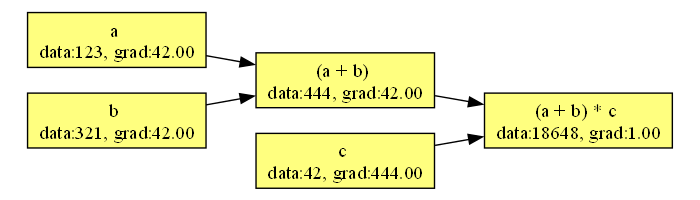
結果はデバッグ出力などで見ても良いのですが、複雑な式の内部情報をそのままコンソールに出力しても見にくいので、 dot ファイルを出力して Graphviz で可視化します。

abcd.dot(&mut std::io::stdout()).unwrap();

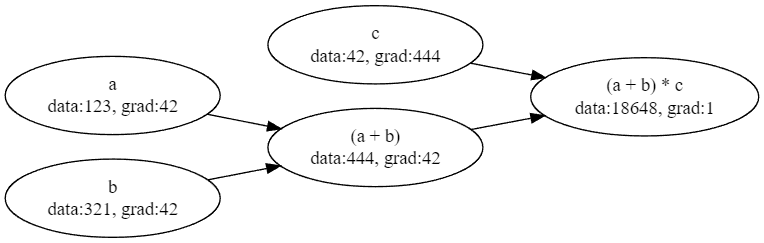
ここでの grad は出力変数に対するそれぞれの変数の偏微分係数、すなわち

$$f = (a + b)c$$

としたときの

$$\frac{df}{da}, \frac{df}{db}, \frac{df}{dc}$$

などを指します。

伝搬の様子をアニメーションにすることもできます。

Rc と参照

rustograd では項は2通りの定義方法があります。一つは参照ベースの Term<'a> で、もう一つは Rc ベースの RcTerm です。

参照ベースのほうが参照カウンタの管理のオーバーヘッドがない分高速ですが、使い方にかなり厳しい制約があります。計算過程の項の全てが計算が終わるまで全て生存していなければなりません。次のように関数から一時変数を除いた項を返そうとしてもコンパイルエラーになります。

fn model<'a>() -> (Term<'a>, Term<'a>) {
    let a = Term::new("a", 1.);
    let b = Term::new("b", 2.);
    let ab = &a * &b;
    (a, ab)
}

このような場合は RcTerm を使うと上手くいきます。

fn model() -> (RcTerm, RcTerm) {
    let a = RcTerm::new("a", 1.);
    let b = RcTerm::new("b", 2.);
    let ab = &a * &b;
    (a, ab)
}

式を構造体の中に入れたいときには特に便利です。 Rust では現時点で Term<'a> を含む自己参照構造体を明示的に作る方法はないからです。また、ライフタイム指定 <'a> も必要ないです(Rc は 'static ライフタイム拘束を持つため)。

一般的には RcTerm が使いやすいですが、参照カウントのコストがあります。

クイズ：参照カウンタが循環参照を削除できなくなることはあるでしょうか？答え：^[2]

一変数関数の追加

式に任意の関数を適用することができます。

例えば、三角関数 sin(a) を適用したいときは次のように apply メソッドを使えます。関数そのものとその微分を関数ポインタとして渡す必要があります。

let a = Term::new("a", a_val);
let sin_a = a.apply("sin", f64::sin, f64::cos);

入力変数を色々変えてみることでグラフもプロットできます。

    for i in -10..=10 {
        let x = i as f64 / 10. * std::f64::consts::PI;
        a.set(x).unwrap();
        sin_a.eval();
        println!("[{x}, {}, {}],", sin_a.eval(), sin_a.derive(&a));
    }

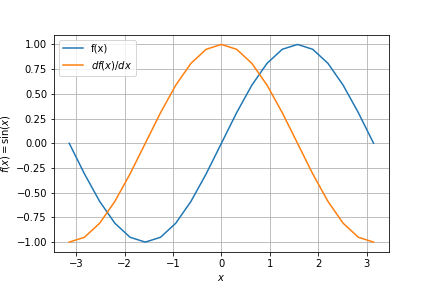
この例はあまりにも単純すぎますが、次のような少し込み入った関数でも微分できます。

let a = Term::new("a", a_val);
let sin_a = a.apply("sin", f64::sin, f64::cos);
let ten = Term::new("5", 5.);
let b = &a * &ten;
let c = Term::new("c", 0.2);
let sin_b = b.apply("sin", f64::sin, f64::cos);
let c_sin_b = &c * &sin_b;
let all = &sin_a + &c_sin_b;

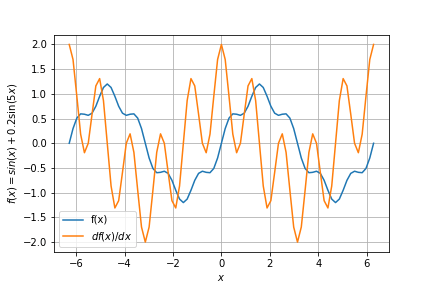
マクロによる省力化

上記のような式を Rust コードで書くのは大変ですね。中間変数の項をすべて変数として定義しなければならないので長くなります。 rustograd にはフィーチャーフラグ macro があり、これを有効にすると rustograd! 手続きマクロを使って簡単に書けます。

例えば、上の例は次のように書けます。

use rustograd_macro::rustograd;

rustograd! {{
    let a = 0.;
    let b = a * 5.;
    let all = sin(a) + 0.2 * sin(b);
}}

この機能を使うには、次のようにフィーチャーフラグを有効にしてください。

cargo r --features macro --example mixed_sine_macro

syn クレートの設計上の都合により、 rustograd! マクロの引数は2重波括弧 {{}} で括る必要があります。

関数を定義するには、スコープ内にその名前の関数を用意し、またその微分を _derive という接尾辞で定義してください。例えば、上記の例で言うと、 sin と sin_derive を次のように定義します。

fn sin(x: f64) -> f64 { x.sin() }
fn sin_derive(x: f64) -> f64 { x.cos() }

実装方法

基本的な実装方法はシンプルです。式の AST を構築し、それを再帰的に処理することによって微分係数を求めます。

参照タイプ Term<'a>

UnarfyFnPayload は一変数関数の内容を記憶する構造体で、対象の関数への関数ポインタとその微分を持ちます。ライフタイムがそこら中に散らかっていますが、全てが AST 全体の寿命を示します。参照でノード間をリンクするので、 Rust の場合はライフタイムだらけになってしまうのは仕方がありません。

#[derive(Clone, Debug)]
struct UnaryFnPayload<'a> {
    term: &'a Term<'a>,
    f: fn(f64) -> f64,
    grad: fn(f64) -> f64,
}

#[derive(Clone, Debug)]
enum TermInt<'a> {
    Value(Cell<f64>),
    Add(&'a Term<'a>, &'a Term<'a>),
    Sub(&'a Term<'a>, &'a Term<'a>),
    Mul(&'a Term<'a>, &'a Term<'a>),
    Div(&'a Term<'a>, &'a Term<'a>),
    UnaryFn(UnaryFnPayload<'a>),
}

項の中身は次のようになります。項の種類によって異なる内容は enum TermInt に含まれ、それ以外は共通部分として TermPayload に置いています。項の名前や評価結果の値と微分係数を記憶します。これらは Cell に包んでいますが、これは式の AST を維持したまま値を書き換えて再評価することを可能にするためです^[3]。

#[derive(Clone, Debug)]
struct TermPayload<'a> {
    name: String,
    value: TermInt<'a>,
    data: Cell<f64>,
    grad: Cell<f64>,
}

最後に、ユーザの目に触れる pub な型がこちらの Term です。実体は Box<TermPayload> ですが自前のメソッドを定義するために newtype パターンで包んでいます。

#[derive(Clone, Debug)]
pub struct Term<'a>(Box<TermPayload<'a>>);

Box に包むことが必要なのかというと、厳密には必要ないと思います。必要なのはライフタイム拘束 <'a> が AST の全てのノードで同じであることで、それはスタック変数でもヒープ変数でも同じように適用できるはずです。しかし、後ほど RcTerm を実装したので、それとの違いを極力避けるために Box に包んでいます。

参照カウンタバージョン RcTerm

参照カウンタバージョンの実装も考え方は同じで、参照の代わりに Rc を使うというだけです。

#[derive(Clone, Debug)]
struct UnaryFnPayload {
    term: RcTerm,
    f: fn(f64) -> f64,
    grad: fn(f64) -> f64,
}

#[derive(Clone, Debug)]
enum TermInt {
    Value(Cell<f64>),
    Add(RcTerm, RcTerm),
    Sub(RcTerm, RcTerm),
    Mul(RcTerm, RcTerm),
    Div(RcTerm, RcTerm),
    Neg(RcTerm),
    UnaryFn(UnaryFnPayload),
}

#[derive(Clone, Debug)]
struct TermPayload {
    name: String,
    value: TermInt,
    data: Cell<f64>,
    grad: Cell<f64>,
}

#[derive(Clone, Debug)]
pub struct RcTerm(Rc<TermPayload>);

パフォーマンス的には Term<'a> が使えるならそれを優先した方が良いですが、利便性は RcTerm が優れますので、借用チェッカーに怒られたら無言で置換すると良いでしょう。

ロジックがほとんど同じなので Term<'a> と RcTerm はジェネリック型にして共通化できないものかと思いましたが、ライフタイムが変わるので簡単にできそうには思えません。これは今後の課題です。

ここから先はライフタイムに惑わされないように RcTerm を使って説明していきます。

フォワードプロパゲーション

肝になるのは値の評価と勾配の評価を再帰的に AST に適用するところです。まずは値の評価を以下に示します。これは元の変数からその関数へと伝搬していくのでフォワードプロパゲーション(という名前があるのかどうか知りませんが、バックプロパゲーションと対比すればそういう概念になります)です。

ポイントになるのは親ノードの eval が自分の値を決めるために使われていることです。このため親は常に子よりも先に評価されます。これによってフォワードプロパゲーションとなります。

内部構造体 TermInt とラップ型 RcTerm で相互再帰していますが、これは計算結果をメンバに覚えておき、後ほど Graphviz でまとめて描画するためです。

impl TermInt {
    fn eval(&self) -> f64 {
        use TermInt::*;
        match self {
            Value(val) => val.get(),
            Add(lhs, rhs) => lhs.eval() + rhs.eval(),
            Sub(lhs, rhs) => lhs.eval() - rhs.eval(),
            Mul(lhs, rhs) => lhs.eval() * rhs.eval(),
            Div(lhs, rhs) => lhs.eval() / rhs.eval(),
            Neg(term) => -term.eval(),
            UnaryFn(UnaryFnPayload { term, f, .. }) => f(term.eval()),
        }
    }
}

impl RcTerm {
    pub fn eval(&self) -> f64 {
        let val = self.0.value.eval();
        self.0.data.set(val);
        val
    }
}

なお、一つの変数に関してのみの微分を行う derive メソッドも同じようフォワードプロパゲーションで実行されます。

バックプロパゲーション

もう一つの方向がバックプロパゲーションです。これは backprop で実行されます。

まずはノードそれぞれの内部バッファをクリアします。これは祖先がシェアされていたときに寄与を加算するために必要です。具体的には $f(x) + g(x)$ の $x$ の微分では $\partial f/\partial x + \partial g/\partial x$ というように2つの中間関数の微分係数の和になることを実現するのに必要です。

また、入り口となる backprop_rec には 1 を引数に渡していますが、これはターゲットとなる関数をそれ自体で微分した時の係数です。

impl RcTerm {
    /// The entry point to backpropagation
    pub fn backprop(&self) {
        self.clear_grad();
        self.backprop_rec(1.);
    }
}

次にプライベートメソッド backprop_rec で再帰的に処理します。ここで self.0.grad.set(self.0.grad.get() + grad); という見にくい文は、単に self.0.grad += grad; を Cell の中身に対して行うものです。この勾配の更新を最初に行ってから親ノードをたどることによって、子ノードが親ノードよりも最初に評価されることになり、バックプロパゲーションとなります。

impl RcTerm {
    /// Assign gradient to all nodes
    fn backprop_rec(&self, grad: f64, callback: &impl Fn(f64)) {
        use TermInt::*;
        let grad_val = self.0.grad.get().unwrap_or(0.) + grad;
        self.0.grad.set(Some(grad_val));
        callback(grad_val);
        let null_callback = |_| ();
        match &self.0.value {
            Value(_) => (),
            Add(lhs, rhs) => {
                lhs.backprop_rec(grad, callback);
                rhs.backprop_rec(grad, callback);
            }
            Sub(lhs, rhs) => {
                lhs.backprop_rec(grad, callback);
                rhs.backprop_rec(-grad, callback);
            }
            Mul(lhs, rhs) => {
                lhs.backprop_rec(grad * rhs.eval_cb(&null_callback), callback);
                rhs.backprop_rec(grad * lhs.eval_cb(&null_callback), callback);
            }
            Div(lhs, rhs) => {
                let erhs = rhs.eval_cb(&null_callback);
                let elhs = lhs.eval_cb(&null_callback);
                lhs.backprop_rec(grad / erhs, callback);
                rhs.backprop_rec(-grad * elhs / erhs / erhs, callback);
            }
            Neg(term) => term.backprop_rec(-grad, callback),
            UnaryFn(UnaryFnPayload { term, grad: g, .. }) => {
                let val = term.eval_cb(&null_callback);
                term.backprop_rec(grad * g(val), callback);
            }
        }
    }
}

一つ一つの演算は普通の微分のルールなので、説明するほどの必要は無いと思いますが、それぞれ以下に対応しています。

• Add

$$f(x) = a(x) + b(x) \Rightarrow \frac{\partial f}{\partial x} = \frac{\partial a}{\partial x} + \frac{\partial b}{\partial x}$$

• Sub

$$f(x) = a(x) - b(x) \Rightarrow \frac{\partial f}{\partial x} = \frac{\partial a}{\partial x} - \frac{\partial b}{\partial x}$$

• Mul

$$f(x) = a(x) b(x) \Rightarrow \frac{\partial f}{\partial x} = a \frac{\partial b}{\partial x} + \frac{\partial a}{\partial x} b$$

• Div

$$f(x) = \frac{a(x)}{b(x)} \Rightarrow \frac{\partial f}{\partial x} = -\frac{a}{b^2} \frac{\partial b}{\partial x} + \frac{1}{b} \frac{\partial a}{\partial x}$$

割り算だけちょっと特殊ルールが入っており、 $\partial b/\partial x$ がゼロだったときは第2項の計算をスキップしています。これは a * b / a のような式においてゼロ割を避けるための苦肉の策で、 AST 全体を見渡せばこの状況を検出して対処できるのではないかと思いますが、今後の課題です。 単純に商の微分計算を間違っていただけでした ^^;

• UnaryFn

$$f(x) = g(h(x)) \Rightarrow \frac{\partial f}{\partial x} = \frac{\partial g}{\partial h} \frac{\partial h}{\partial x}$$

手続きマクロによる簡潔な表現

Rust では手続きマクロ(procedural macros)によってコンパイル時メタプログラミングができます。これは Rust の構文を解析して好きなように書き換えられるということです。

しかし、このためにはいくつか制約があります。一つは手続きマクロは専用の crate に隔離されなければならないということです。これは Rust の翻訳単位が crate であることを考えれば自然な話で、他のコードを書き換えるためにはまず手続きマクロのコードがコンパイルされなければならないということです。

もう一つは手続きマクロ用の crate からは手続きマクロ以外のシンボルは公開できないということです。普通の関数や型を公開する普通の crate としても機能するようにはできません。このため多くのライブラリでは普通の関数用と手続きマクロ用の crate の共通部分がさらに別の crate として用意されています。

rustograd では、リポジトリ内に rustograd-macro という crate を作ってこれを実現しています。これは機能としてはシンプルで、次のようなマクロ呼び出しを

    rustograd! {{
        let a = 0.;
        let b = a * 5.;
        let all = sin(a) + 0.2 * sin(b);
    }}

次のように書き換えるだけです。

    let a = ::rustograd::RcTerm::new("a", 0.);
    let _a1 = ::rustograd::RcTerm::new("_a1", 5.);
    let _a2 = &a * &_a1;
    let b = _a2;
    let _a4 = a.apply("sin", sin, sin_derive);
    let _a5 = ::rustograd::RcTerm::new("_a5", 0.2);
    let _a6 = b.apply("sin", sin, sin_derive);
    let _a7 = &_a5 * &_a6;
    let _a8 = &_a4 + &_a7;
    let all = _a8;

マクロ内の let 宣言で名前の付いた変数は外部でもそのまま参照できます。中間変数は自動的に名前が付けられて AST を構築します。

ただし、手続きマクロで Rust のコードを解析するには syn, quote, proc-macro2 といった依存ライブラリが必要になるので、 feature フラグにしてあります。

まとめ

非常にシンプルなライブラリですが、基本的な式については自動微分ができるシステムができました。思ったほど難しくはなかったです。

実は関数型言語でもできないかな？と思って Haskell でやろうとしてみたのですが、バックプロパゲーションの本質はノードの変更を行うことなので、純粋関数型言語では簡単にはできませんでした。 AST 全体を変数とすればできなくはないでしょうが、あまりやりたいとは思えません。実質的にロジックをステートマシンに書き換えるということに相当します(BehaviorTreeでやりたかったことの逆です)。このような状態の変更を伴うロジックは逐次型プログラミング言語がやはり向いています。

今後の課題

• 多変数関数への対応 (pow 等)
• ディープラーニングに組み込むために、テンソル型(DeepRender では Matrix 型)に適用できるようにする
• コードの重複を避けるため Term<'a> と RcTerm の参照型を型引数とする(できるかな？)
• コンパイル時だけではなく、実行時に任意の式入力に対応するため、専用のパーサを作る^[4]
• ゼロ割問題のように AST 全体を対象とした最適化
• 定数は backprop しないようにする
• さらに効率化するためにメモリアリーナを使って Rc を排除する

脚注

1. [2023/7/26追記] その後の調べで、これは自動微分の世界では Reverse-mode automatic differentiation と呼ばれているものであることがわかりました。言葉としては知っていましたがニューラルネットワークのバックプロパゲーションを意味しているとは思いませんでした ^^;

2. ありません。式は既存の式からしか作れないため、 DAG (非循環有向グラフ)になるからです。もし作れたとしたら自動微分は無限再帰を起こしスタックオーバーフローを起こすでしょう。

3. Cell は RefCell と違って実行時オーバーヘッドはありません。唯一の制約は中身への参照が取れないことです。このライブラリでは data や grad への参照を使う機会はありませんので、 Cell に包むのは実質的にノーコストです。

4. 実行時に専用のパーサが必要なのは、手続きマクロは Rust のパーサを部分的に流用しているためです。幸い Rust には構文解析ライブラリが充実しているのでそれほど難しくはないでしょう。