📸

Rust でレイトレーシングレンダラーをディープラーニングしてみた

2023/06/11に公開

何が何だかわからないタイトルですが、次のような3Dのレンダラーをディープラーニングで模倣してみようということです。左側が訓練データ、右側がディープラーニングした結果でレンダリングしたものです。

まず、私はディープラーニングの専門家ではありませんので、この記事は自分の学習過程を記録したものになります。

今回はディープラーニングというかニューラルネットワーク一般の理解を深めるため、全てをフルスクラッチで実装してみました。行列の掛け算から誤差逆伝搬法まで。このため学習過程を可視化するGUIを作りました。これは全て CPU で動作するので速度は期待しないでください。

リポジトリはこちらです。

https://github.com/msakuta/DeepRender

ブラウザ上で動作する WebAssembly 版もありますが、ファイルから画像をロードする機能はありませんし、ネイティブ版より遅いです。

https://msakuta.github.io/DeepRender/

ニューラルネットワークの基本

ニューラルネットワークおよびディープラーニングの理論的基礎は、腐るほど教材が出回っているので、ここで解説するのも野暮というものでしょう。しかし最低限の解説はしておきたいと思います。

とはいうものの、ここのセクションは理論ばかりで面白くないので飛ばしても良いです。また、ここで書いたことはこちらのPDF(英語)でtypstを使ってまとめたものの簡易版なので、そちらのほうが読みやすいかと思います。正直、 Zenn であまり長いドキュメントを書くのは快適ではありません^[1]。

活性化関数

ニューラルネットワークのはしりは Frank Rosenblatt によるパーセプトロンです。 Rosenblatt が最初に提唱したパーセプトロンの活性化関数は下図に示すようなステップ関数でした^[2]。これはニューロンのモデルが発火と鎮静の2つの状態を持つと考えられていたことに由来します。

S(x) = \begin{cases} 1 & \mathrm{0 < x} \\ 0 & \mathrm{otherwise} \end{cases}

しかし、その後のバックプロパゲーションのために連続な導関数が必要となったことで、シグモイド関数が活性化関数として使われることが多くなりました。これは変数域の全範囲で微分係数を持つという点でバックプロパゲーションに非常に有利ですが、ニューロンの物理モデルに根拠があるわけではありません。また、値域が0から1までと固定されており、任意の関数を近似できないことと、勾配消失問題を抱えており、欠点がないわけではないです。

\sigma(x) = \frac{1}{1+e^{-x}}

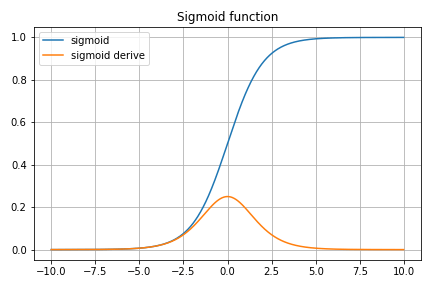
そこで最近よく使われているのが ReLU (Regularized Linear Unit) です。この関数は単純な線形であるため計算コストの比較的高価な指数関数を必要とせず、値域が0から∞まであり、導関数が定義できます。ここまで計算の都合に合わせてしまうと、元のニューロンの活性化モデルの原型をとどめていません。

R(x) = \begin{cases} x & \mathrm{0 < x} \\ 0 & \mathrm{otherwise} \end{cases}

ReLU には計算が簡単で $x$ が正の領域では勾配が一定であるという利点がありますが、負の領域では勾配がゼロになってしまうので、バックプロパゲーションが機能しなくなってしまうという欠点があります。このため考案されたものの一つが SiLU (Sigmoid Linear Unit) です。この他にも ReLU の変種はいろいろありますが、基本的には $x$ の負の領域でも勾配を持つようにしたものが多いです。

\mathrm{SiLU}(x) = \frac{x}{1+e^{-x}}

さらに本プロジェクトで使用した中でも特殊なのは、単純な三角関数です。値域をシグモイド関数と合わせるために $[0, 1]$ にスケールしています。こんなものでも活性化関数として使えるのは驚きですが、非線形性と勾配が計算できる関数であれば何でも活性化関数にできるということの一例として興味深いところです。

\frac{\sin(x) + 1}{2}

フィードフォワードニューラルネットワーク

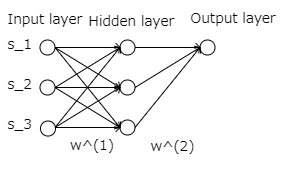
ニューラルネットワークは複数のパーセプトロンを集めた層(レイヤー)を重ねたものです。このため厳密な名前として MLP (Multilayer Perceptron) とも呼ばれます。層の間では重みを掛けて次の層へ信号を伝えます。次の例では $w^{(1)}, w^{(2)}$ といった記号で重み行列を表します。ここで上付きの $(1)$ などは層の階数を表しますが、べき乗との区別のため括弧で括っています。また、 $s_i$ は入力信号を表します。

重み行列は、前の層の信号と同じ数の列数と次の層の入力と同じ数の行数を持ちます。

s_j^{(1)} = f\left(\sum_{i=1}^n w_{ij}^{(1)} s_i\right)

ここで $f(\cdot)$ は前節で述べた活性化関数です。

さらに、第2層の重みを $w^{(2)}_{jk}$ とすると、出力層における信号 $s^{(2)}_k$ は次のようになります。

\begin{equation} s_k^{(2)} = f\left(\sum_{j=1}^n w_{jk}^{(2)} s_j^{(1)}\right) \end{equation}

ここまでの議論を繰り返していけば任意の層のニューラルネットワークの出力を計算することができます。なお、このように前段の全てのニューロンが次につながっているアーキテクチャを全結合 (Fully connected) 層と言います。画像認識などの分野では Convolutional Neural Network のように全結合でないものもありますが、本プロジェクトでは全結合のみを扱います。

フィードフォワードとはこのネットワーク上で信号を順方向に送ることです。

バイアス項

実用上は、前の層からの影響を受けない、定数の入力を各層に置くことが多いです。これらの入力をバイアスと呼びます。

これがどう役に立つかというと、活性化関数の引数に定数項の自由度を持たせることになります。たとえば入力層の最後のシグナルは次のように変形できます。

s_j^{(1)} = f\left(w_{nj} + \sum_{i=1}^{n-1} w_{ij}^{(1)} s_i\right)

これは実質的に活性化関数の原点を $−w_{nj}$ だけずらしたということです。こうして原点のオフセットを重み行列の中に入れることができ、オフセットを別途最適化の対象として考えなくても済みます。

バックプロパゲーション

バックプロパゲーションは誤差逆伝搬とも呼ばれますが、ディープラーニングで鍵となる技術です。

まず、誤差関数 $L$ というものを定義します。これは正しい答え $A_k$ と予測された答え $s^{(2)}_k$ とのずれの大きさを示す指標です。ここでは次のように定義するがその理由はすぐに明らかになります。

L = \frac{1}{2}\sum_k(A_k - s_k^{(2)})^2

まず、出力層の重み $w^{(2)}_{jk}$ をどのように修正すれば正しい答えに近づくかを考えてみます。これは $L$ を減らす向きの変化を探すということですから、 $\frac{\partial L}{\partial w^{(2)}_{jk}}$ を求め、学習速度パラメータ $\delta$ をかけたものを差し引いて次のステップの重みとすればよいです。ここで $t$ はタイムステップです。

w_{jk}^{(2)}|_{t+1} = w_{jk}^{(2)}|_t - \delta \frac{\partial L}{\partial w_{jk}^{(2)}|_t}

これは最適化問題における最急降下法(gradient descent method)にあたりますが、多鋒性のある解空間において局所解に落ち込まないかという点については dropout に関していつか書くかもしれません。

ここで右辺第2項を計算すると、微分の連鎖則(chain rule)^[3]より

\begin{align*} - \delta \frac{\partial L}{\partial w_{jk}^{(2)}} &= - \delta \frac{\partial L}{\partial s_k^{(2)}} \frac{\partial s_k^{(2)}}{\partial w_{jk}^{(2)}} \\ &= -\delta (A_k - s_k^{(2)}) \frac{\partial s_k^{(2)}}{\partial w_{jk}^{(2)}} \end{align*}

となって、教師信号の答えと予測した答えの差だけから簡単に計算できます。

さて、ここで後半の $\frac{\partial s^{(2)}_k}{\partial w^{(2)}_{jk}}$ を考えてみると、活性化関数 $f$ を通して (1) のように関係しているので、まず $f$ の引数に渡されている和を中間変数 $p_k$ とおきます。

p_k \equiv \sum_{j=1}^n w_{jk}^{(2)} s_j^{(1)}

すると、ここでも chain rule を使って

\frac{\partial s_k^{(2)}}{\partial w_{jk}^{(2)}} = \frac{\partial s_k^{(2)}}{\partial p_k} \frac{\partial p_k}{\partial w_{jk}^{(2)}}

となる。 $\frac{\partial s^{(2)}_k}{\partial p_k}$ は活性化関数の導関数 $f'$ です。また、

\begin{align*} \frac{\partial p_k}{\partial w_{jk}^{(2)}} &= \frac{\partial}{\partial w_{jk}^{(2)}} \sum_{j=1}^n w_{jk}^{(2)} s_j^{(1)} \\ &= s_j^{(1)} \end{align*}

となることを使って

\frac{\partial s_k^{(2)}}{\partial w_{jk}^{(2)}} = s_j^{(1)} f'(p_k)

と表せます。全体を改めて書くと、

w_{jk}^{(2)}|_{t+1} = w_{jk}^{(2)}|_t - \delta (A_k - s_k^{(2)}) s_j^{(1)} f'(p_k)

となります。

ここから明らかなようにバックプロパゲーションには活性化関数の導関数が求められることが必要です。

さらに、隠れ層の重み $w^{(1)}_{ij}$ がどうなるか考えてみます。上式の重みを $w^{(1)}_{ij}$ に置き換えればよいのですが、 chain rule の適用方法が変わってきます。最終的に求めたい重みのインデックス $i,j$ ではない $k$ が中間の変数に入ってくるため、偏微分ではなく全微分が間に入ってきます。

\begin{align*} \frac{\partial L}{\partial w_{ij}^{(1)}} &= \sum_k \frac{\partial L}{\partial s_k^{(2)}} \frac{\partial s_k^{(2)}}{\partial w_{ij}^{(1)}} \\ &= \sum_k \frac{\partial L}{\partial s_k^{(2)}} \frac{\partial s_k^{(2)}}{\partial s_j^{(1)}} \frac{\partial s_j^{(1)}}{\partial w_{ij}^{(1)}} \end{align*}

ここで $\frac{\partial L}{\partial s^{(2)}_k}$ は実は前段で計算した $A_k − s^{(2)}_k$ に他なりません。これを使って計算の一部を再利用することができます。 2層程度のニューラルネットワークではご利益の実感がわきませんが、実は隠れ層の深さを深くしていくと、中間変数が増えていくため、計算が再利用できる部分がどんどん増えていきます。つまり、出力側から先に計算していけば、次の段で再利用できる計算結果があるということです。特に、層あたりの重み係数の数を底とする層の深さのべき乗のオーダーで計算量が増えていくため、計算を再利用することは深いニューラルネットワークにおいては重要です。このアルゴリズムの考え方は FFT のバタフライ演算に少し似ている気がします。

こうして、出力側から入力側の順で計算を行うため、バックプロパゲーションと呼ばれます。

バッチ訓練

前のセクションの誤差関数は一つのサンプルについての結果でした。これを $N$ 個のサンプルについてまとめて計算すると、そろそろ添え字のスペースがなくなってきましたが、上付きの $[l]$ で $l$ 番目のサンプルを表すことにすると、次のようになります。

L = \frac{1}{2} \sum_{l=1}^N \sum_k \left( A_k^{[l]} - s_k^{(2)[l]} \right)^2

偏微分はサンプルごとに独立になるので、再急降下法の勾配項は、次のようになります。

\begin{align*} -\delta \frac{\partial L}{\partial w_{jk}^{(2)}} &= -\delta \sum_{l=1}^N \frac{\partial L}{\partial s_k^{(2)[l]}} \frac{\partial s_k^{(2)[l]}}{\partial w_{jk}^{(2)}} \\ &= -\delta \sum_{l=1}^N \left( A_k - s_k^{(2)[l]} \right) \frac{\partial s_k^{(2)[l]}}{\partial w_{jk}^{(2)}} \\ &= -\delta \sum_{l=1}^N \left( A_k - s_k^{(2)[l]} \right) s_j^{(1)[l]} f'\left( \sum_{j=1}^N w_{jk}^{(2)} s_j^{(1)[l]} \right) \end{align*}

隠れ層の勾配も同じように計算できることは自明なので省略します。

このように、複数のサンプルの損失関数から勾配方向を一度に求める方法をバッチ訓練といいます。これに対して、前節でみたように一つずつサンプルから勾配方向を計算し下っていくのをオンライン訓練とか確率的勾配降下法(stochastic gradient descent)といいます。また、間をとって一口サイズに区切ったサンプルサイズで繰り返し訓練するミニバッチといわれる方法もあります。下記のようにそれぞれ一長一短あります。

バッチ訓練はばらつきのあるデータを平滑化した勾配を下るため安定性が高く、収束が早めである
オンライン訓練は個々のデータのノイズに振り回されるので収束性は悪いが、メモリに入らないような非常に大きな訓練データでも適用できる

実装

行列

まずは基本となる行列の実装です。単純に行数と列数とフラット化したペイロードで表現します。

#[derive(Clone, PartialEq, Debug)]
pub(crate) struct Matrix {
    rows: usize,
    cols: usize,
    v: Vec<f64>,
}

行列の基本的なコンストラクタや zeros などの numpy ライクなインターフェースを用意します。 new は利便性のために固定長配列を引数に取り、そのサイズをジェネリック引数で判定して直接構築しています。

impl Matrix {
    pub(crate) fn new<const R: usize, const C: usize>(m: [[f64; C]; R]) -> Self {
        Self {
            rows: R,
            cols: C,
            v: m.into_iter().flatten().collect(),
        }
    }

    pub(crate) fn from_slice<const C: usize>(m: &[[f64; C]]) -> Self {
        Self {
            rows: m.len(),
            cols: C,
            v: m.iter().flatten().copied().collect(),
        }
    }

    pub(crate) fn zeros(row: usize, col: usize) -> Self {
        Self {
            rows: row,
            cols: col,
            v: vec![0.; row * col],
        }
    }
}

また、 Rust では演算子のオーバーロードが std::ops::Mul トレイトの実装で可能なので、行列の掛け算も直感的に書けます。

impl std::ops::Mul for &Matrix {
    type Output = Matrix;
    fn mul(self, rhs: Self) -> Self::Output {
        assert_eq!(self.cols, rhs.rows);
        let mut v = vec![0.; self.rows * rhs.cols];
        for r in 0..self.rows {
            for c in 0..rhs.cols {
                v[r * rhs.cols + c] = self.v[r * self.cols..(r + 1) * self.cols]
                    .iter()
                    .zip(0..self.cols)
                    .map(|(s, oi)| s * rhs.v[oi * rhs.cols + c])
                    .fold(0., |acc, cur| acc + cur)
            }
        }
        Matrix {
            rows: self.rows,
            cols: rhs.cols,
            v,
        }
    }
}

直感的に書けるとは言っても、 C++ ほどではありません。 Rust では C++ と違って参照は暗黙的には取得されないので、掛け算は次のように書く必要があります。

let interm = &signal_biased * &weights;

これは Mul トレイトのレシーバに &Matrix を取っているからですが、そうしないと Matrix が消費されてしまうからです。掛け算では Matrix を読み取るだけで元のオブジェクトを破壊したくないわけですが、 Matrix は Vec を内部に持つので、 Copy にはなれません。このため参照を使って所有権の移動を避ける必要があります。

モデル

学習の実行モデルは、次のような構造体で表現します。

pub(crate) struct Model {
    arch: Vec<usize>,
    weights: Vec<Matrix>,
    activation: fn(f64) -> f64,
    activation_derive: fn(f64) -> f64,
    optimizer: Box<dyn Optimizer>,
}

arch はニューラルネットワークのアーキテクチャを表すものです。最初と最後の要素はそれぞれ入力と出力の変数を表し、その間は中間層の信号の数を表します。

weights は層ごとの重み行列を表します。

activation と activation_derive は活性化関数とその導関数を表します。自動微分などの機能はありませんので手で導関数を計算する必要があります。この構造だと層ごとに異なる活性化関数を使えませんが、それは現時点でのこのプログラムの制約です。

optimizer は最適化アルゴリズムを表すトレイトオブジェクトです。 SteepestDescentOptimizer と AdamOptimizer があります。

本プロジェクトで最も苦労したのが、バックプロパゲーションの理論をコードに置き換えるところです。フィードフォワードで計算した中で再利用できるものを LayerCache として覚えておき、バックプロパゲーションのときに計算を削減しています。ここのコードは何度直しても動くようにならず苦労しましたが、最終的には動作しました。

impl Model {
    fn learn_iter(&mut self, rate: f64, samples: &Matrix) {
        struct LayerCache {
            signal: Matrix,
            interm: Matrix,
        }

        // Forward propagation
        let mut signal = samples.cols_range(0, samples.cols() - 1);
        let mut layer_caches = vec![];
        for weights in self.weights.iter() {
            let signal_biased = signal.hstack(&Matrix::ones(signal.rows(), 1));
            let interm = &signal_biased * &weights;
            signal = interm.map(self.activation);
            layer_caches.push(LayerCache {
                signal: signal_biased,
                interm,
            });
        }

        // Back propagation
        let mut loss = samples.col(samples.cols() - 1) - signal;

        for ((l, layer_cache), weights) in layer_caches
            .iter()
            .enumerate()
            .zip(self.weights.iter_mut())
            .rev()
        {
            let interm_derived = layer_cache.interm.map(self.activation_derive);
            let weights_shape = weights.shape();
            let signal_biased = &layer_cache.signal;
            let mut diff = Matrix::zeros(weights_shape.0, weights_shape.1);
            for i in 0..weights_shape.0 {
                for j in 0..weights_shape.1 {
                    let mut diff_sum = 0.;
                    for l in 0..loss.rows() {
                        diff_sum += loss[(l, j)] * signal_biased[(l, i)] * interm_derived[(l, j)];
                    }
                    diff[(i, j)] = diff_sum;
                }
            }
            *weights += self
                .optimizer
                .apply(l, &diff)
                .scale(rate / samples.rows() as f64);
            let loss_derived = loss.elementwise_mul(&interm_derived);
            loss = &loss_derived * &weights.t().cols_range(0, weights.rows() - 1);
        }
    }
}

最適化アルゴリズム

最適化アルゴリズムで最も簡単なのは、前述の再急降下法です。しかし、このアルゴリズムは収束性が悪い場合があり、いろいろな最適化アルゴリズムが開発されています。ここでは Adam と呼ばれるものを実装しています。

Adam のアルゴリズムは原論文が割と分かり易いのでここでは説明しませんが、 Rust での実装は次の通りで、それほど複雑なものではありません。

pub(crate) struct AdamOptimizer {
    t: f64,
    momentum1: Vec<Matrix>,
    momentum2: Vec<Matrix>,
}

impl AdamOptimizer {
    fn new(shapes: &[usize]) -> Self {
        let momentum = shapes_to_matrix(shapes, |(n, m)| Matrix::zeros(*n + 1, *m));
        Self {
            t: 0.,
            momentum1: momentum.clone(),
            momentum2: momentum,
        }
    }
}

const BETA1: f64 = 0.9;
const BETA2: f64 = 0.999;
const EPSILON: f64 = 1e-8;

impl Optimizer for AdamOptimizer {
    fn apply(&mut self, l: usize, diff: &Matrix) -> Matrix {
        self.t += 1.;
        let momentum1 = &mut self.momentum1[l];
        for (m, d) in momentum1.zip_mut(diff) {
            *m = BETA1 * *m + (1. - BETA1) * *d
        }
        let momentum2 = &mut self.momentum2[l];
        for (m, d) in momentum2.zip_mut(diff) {
            *m = BETA2 * *m + (1. - BETA2) * d.powf(2.)
        }
        let mut momentum1hat = momentum1.scale(1. / (1. - BETA1.powf(self.t)));
        let momentum2hat = momentum2.scale(1. / (1. - BETA2.powf(self.t)));
        for (m1, m2) in momentum1hat.zip_mut(&momentum2hat) {
            *m1 /= m2.sqrt() + EPSILON;
        }
        momentum1hat
    }
}

サンプラー

このプロジェクトでは、訓練データをバッチとして取り出すロジックを Sampler トレイトとして抽象化しています。これは、後ほどレイトレーシングレンダラーで真のランダムサンプリングを行うためです。

#[derive(Clone, Copy, PartialEq, Eq, Debug)]
pub(crate) enum TrainBatch {
    Sequence,
    Shuffle,
    Full,
}

pub(crate) trait Sampler {
    fn sample(&mut self, train_batch: TrainBatch, batch_size: usize) -> Matrix;
    fn full(&self) -> &Matrix;
}

Sampler トレイトの sample メソッドは、バッチのサンプリング方法を示す TrainBatch と、バッチサイズを引数に取り、 Matrix を返します。

TrainBatch::Sequence は、訓練データの先頭から順にバッチサイズを切り出して返すモードです。単純ですが入力に偏りがあるデータでは次の Shuffle のほうが確率的再急降下法の「探索」効果が高いです。

TrainBatch::Shuffle は、訓練データをランダムに並べ替えてからバッチに切り出す方法です。統計的に勾配にランダム性が追加されやすく、訓練初期の解から遠い段階で解空間を探索するのに効率が良いです。

TrainBatch::Full は、訓練データ全体を一つのバッチとして勾配を計算する方法です。安定度は抜群ですが、すべての訓練データの損失を計算するので時間がかかります。

ここでは通常の訓練データを行列で表現する MatrixSampler という実装を解説します。
MatrixSampler 構造体は、訓練データと順番を表す Vec を持ちます。 TrainBatch::Sequence が指定されたときは order には [0, 1, ...] という順番でインデックスが入りますが、 TrainBatch::Shuffle の場合は rand クレートの shuffle メソッドを使って混ぜます。 TrainBatch::Full の場合は単純に訓練データ全体を返します。

pub(crate) struct MatrixSampler {
    train: Matrix,
    order: Vec<usize>,
}

impl Sampler for MatrixSampler {
    fn sample(&mut self, train_batch: TrainBatch, batch_size: usize) -> Matrix {
        match train_batch {
            TrainBatch::Sequence => {
                if self.order.is_empty() {
                    self.order = (0..self.train.rows()).collect();
                }
                let samples = batch_size.min(self.order.len());
                let mut train = Matrix::zeros(samples, self.train.cols());
                for j in 0..samples {
                    train
                        .row_mut(j)
                        .copy_from_slice(self.train.row(self.order.pop().unwrap()));
                }
                train
            }
            TrainBatch::Shuffle => {
                if self.order.is_empty() {
                    self.order = (0..self.train.rows()).collect();
                    self.order.shuffle(&mut rand::thread_rng());
                }
                let samples = batch_size.min(self.order.len());
                let mut train = Matrix::zeros(samples, self.train.cols());
                for j in 0..samples {
                    train
                        .row_mut(j)
                        .copy_from_slice(self.train.row(self.order.pop().unwrap()));
                }
                train
            }
            TrainBatch::Full => self.train.clone(),
        }
    }

    fn full(&self) -> &Matrix {
        &self.train
    }
}

アプリケーション

XOR ゲート

恐らく最も簡単なニューラルネットワークの学習例が論理ゲートの XOR です。これは2つのブーリアン値を入力に取り、一つを出力する関数と見なせます。真理値表を書くと次のようになります。

	0	1
0	0	1
1	1	0

簡単に見えますが、中間層がないと表現できないことが分かっています。^[4]

学習の結果を示したのが下のスクリーンショットです。右下にそれぞれの入力に対応する出力を表示しています。正確に 0 と 1 にはなっていませんが、ほとんど正しい値になっていることがわかります。正確な値にならないのはニューラルネットワークの宿命で、信号の連続性(=微分可能性)を基礎に置いている以上、離散値の厳密な値に一致はしません。

GUI では、学習の過程の損失関数や重み行列の中身もプロットしており、時間とともにどう変化していくかが見て取れます。

1変数関数

次の課題は、1変数関数です。ここでは三角関数を模倣してみます。ここでは中間層2層、12個のパーセプトロンで試してみます。

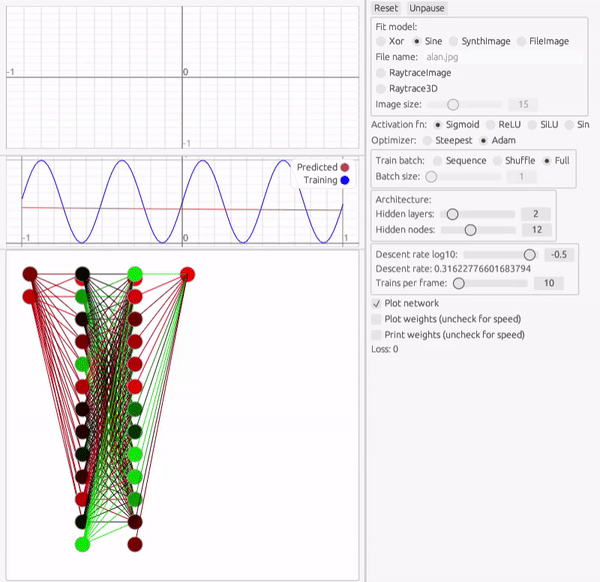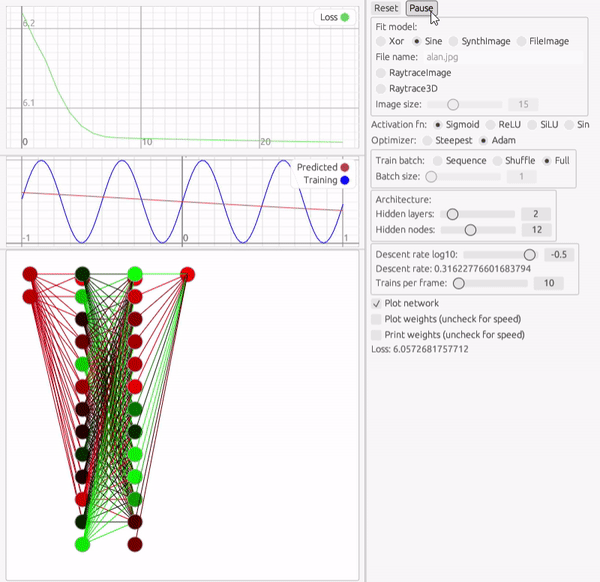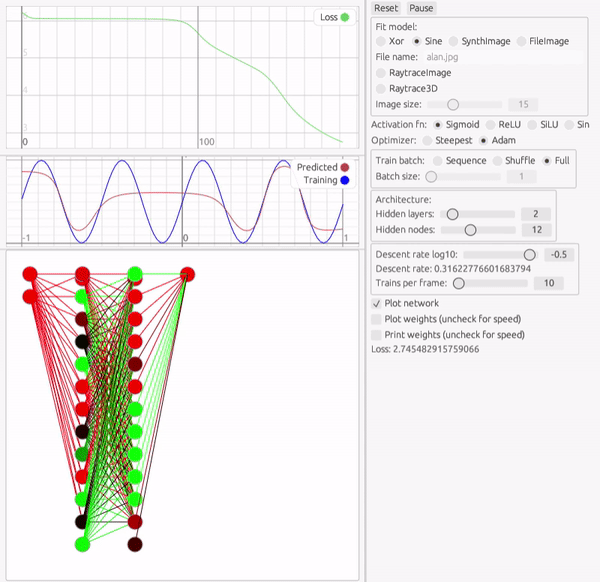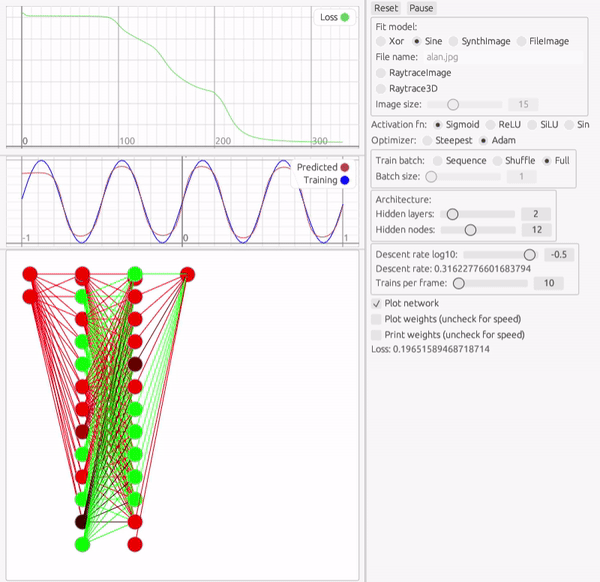
最適化アルゴリズムやアーキテクチャの調整は多少必要ですが、かなりの速度で学習できていることが分かります。

画像(2変数関数)

ここで扱う画像は、多くのディープラーニングの製品と異なり、ピクセルごとに異なる入力チャンネルにするのではなく、2変数関数としてモデル化します。

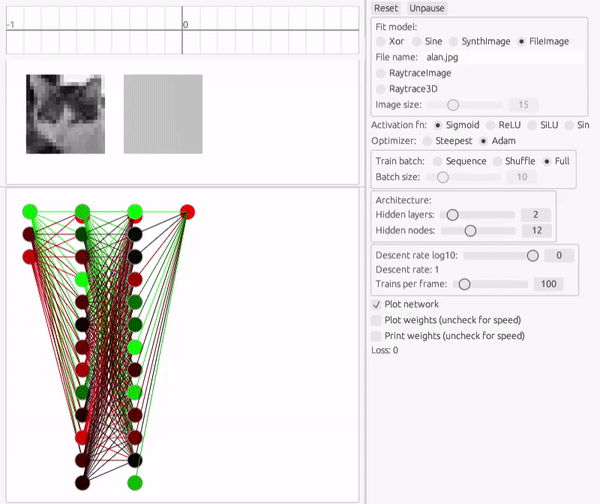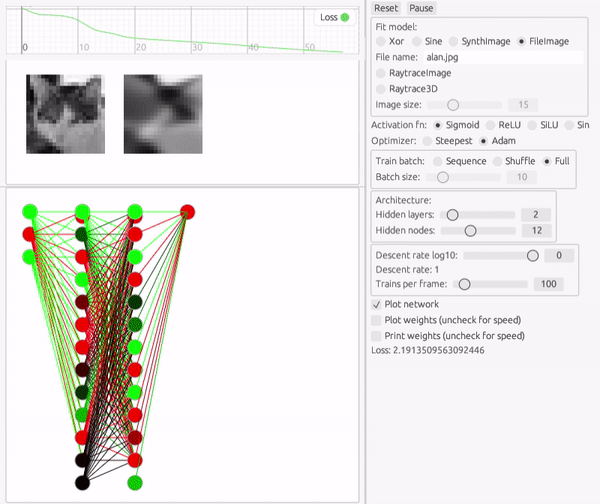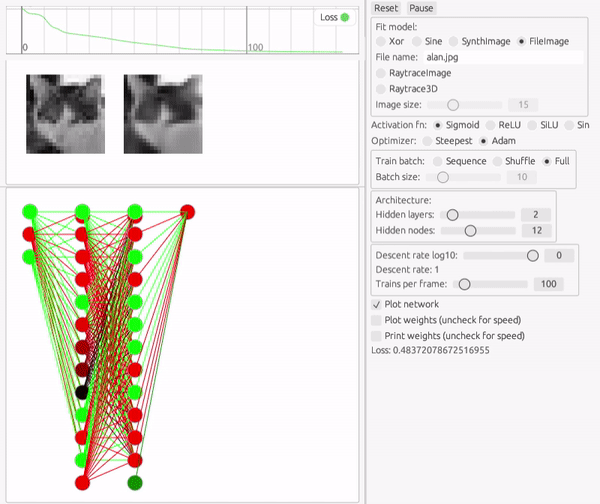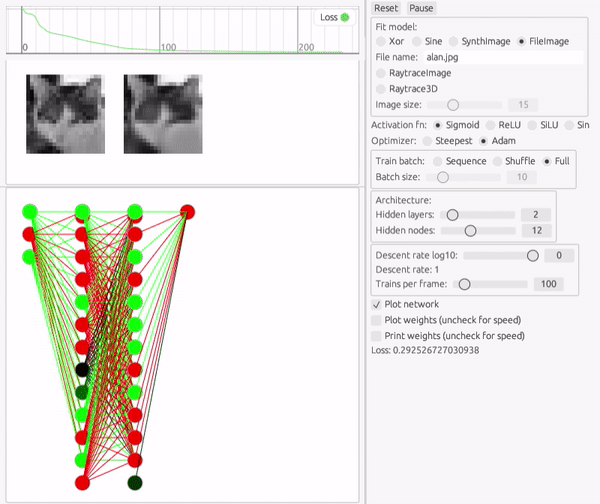
入力が2変数になっただけで、本質的には先ほどの三角関数へのフィットと大して変わりません。

レイトレーシング画像

さて、画像が学習できるなら3次元のシーンも学習できるはずです。ここではだいぶ昔に作ったray-rustというプロジェクトをクレート化して外部ライブラリとして参照することで動的にレンダリングを行った結果を学習データとします。このようなコードの再利用は Rust では本当にやりやすいと感じます。

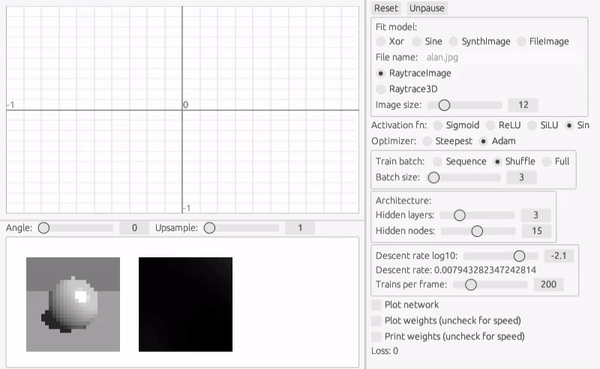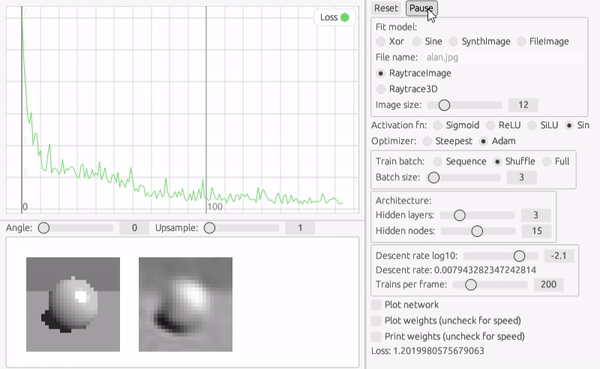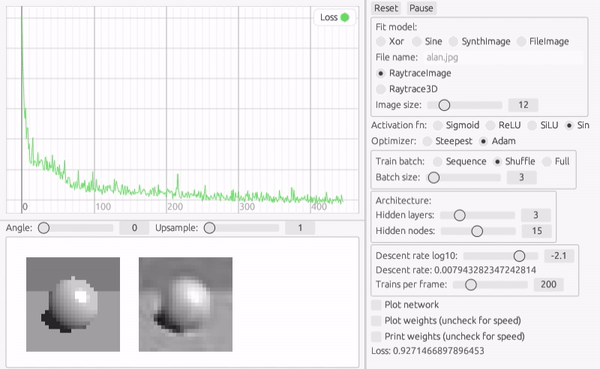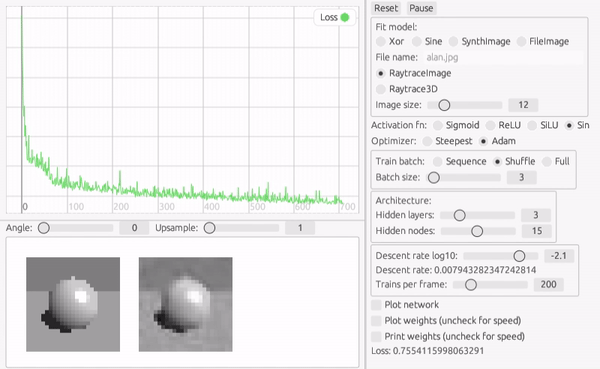
画像がふらついて見えるのは、バッチ訓練と Shuffle の効果です。毎回訓練セットの順番が変わるので、勾配の方向が少しずつ変わっているのです。このように訓練データにランダム性を持たせることで統計的に解に近づいていく方法を確率的再急降下法 (Stochastic Gradient Descent) といいます。

この方法のメリットは、訓練データ全体を評価しなくても最適化ステップが進むので、学習が早い傾向にあることと、勾配が少ない鞍部点に滞留しているような時に抜け出すのに役立つことです。
このようなシャープなエッジを含む画像だと、初期のパラメータが滞留して損失関数の壁を越えられない場合が多いような気がします。そのような場合には Shuffle したミニバッチには効果があります。

3次元シーン

ここでさらに変数を増やして、カメラの位置を入力変数として学習してみます。下のアニメでも見て取れるように、訓練中でもカメラの角度をリアルタイムに変えて見れます。

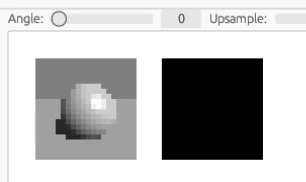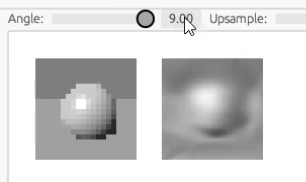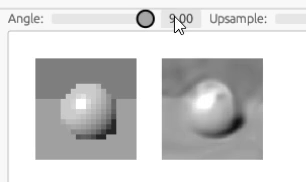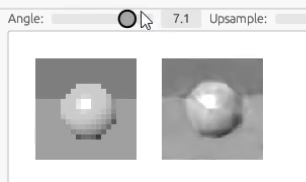
ここら辺になってくると訓練にも時間がかかるので、全ての過程をアニメーションにはできませんが、結果だけ示すと次のようになります。

さらに、解像度を上げるため、サンプラーに工夫を加えます。我々はレイトレーシングレンダラーを持っていますので、事前に訓練データを行列で用意しておく代わりに、毎回ランダムな光線を発射してサンプルを取得することができます。原理的にはこの方法で画像のピクセルや回転角の量子化効果を避け、本当のモデルのサンプリングを行うことができるはずです。

このサンプリングは RaytraceSampler で実装していますが、これを説明するとレイトレーシングの記事になってしまいそうなので割愛します。

また、画像サイズが入力よりも大きくなるので、レンダリング用にアップサンプルする機能も付けます。

これにより学習した結果が、冒頭にも掲載したこのアニメーションです。

解像度や回転角度が元画像よりもスムーズになっているのが見て取れると思います^[5]。ちなみに、元画像は損失関数の評価に使っているので、あまり高解像度にすると学習速度に影響してしまいます。このため 30x30 ピクセルの比較的小さい画像にしてあります。

この例では、隠れ層 4 層、パーセプトロン数 26 個、活性化関数 SiLU、バッチは Shaffle の 10 サンプル、学習速度 10^-3.5 といったパラメータで学習しています。

ちなみに、活性化関数を三角関数に変えてみると次のようになります。

そもそも三角関数で学習できるということ自体が少々驚きですが、境界線がややぼやけているのと、黒いはずの部分に周期的な縞模様が見えています。これは SiLU と違って明確な境界を持たない活性化関数の表れだと思われます。別の言い方をすると jpeg のリンギングノイズと同種のものです。

[2023/6/30 追記] 重み行列の画像表現

ちょっと改変を施して重み行列を画像として表示する機能を加えました。

従来はニューロン同士の接続を線で表し、赤色で負の、緑色で正の重みを表現していましたが、これだとモデルの規模が大きくなってきたときに何が何だかわからなくなります。

元々は行列なので、画像として表現するのは簡単です。行は前の層のニューロンに相当し、列は次の層のニューロンの入力に相当します。画像で表現することでそれぞれの重みの様子が一目で把握しやすくなります。

すでに上の画像でもいくつかの気づきが得られます。例えば、第二隠れ層の重みのいくつかの行は、他の行に比べて重みが小さいことが分かります。これは前段のニューロンにほとんど結果への影響力がないことを表します。つまり「死んだ」ニューロンを示唆します。

さらに全体を通して見ると後段の層の重みのほうが色が薄い(=重みの絶対値が小さい)ことがわかります。これは前段がバックプロパゲーションの影響を受けて変動しやすいことを示します。また後段の重みの表現力が全て生かされていないことを示します。これは正則化などの手法によって改善できるかもしれません。

可視化によって得られる知見は想像以上のものがあります。何よりも見ていて飽きません。

まとめ

Rust でディープラーニングフレームワークを一から実装してみました。
CPU で動作するので速度は遅いですが、学習の過程をリアルタイムに可視化することができ、また学習速度などの一部のパラメータはリアルタイムに調整も可能です。
色々な活性化関数や最適化アルゴリズム、ニューラルネットワークのアーキテクチャやバッチ訓練の方法を変えて遊んでみることで、それぞれの特性や得意な点がよくわかりました。
ニューラルネットワークの特性である「万能関数近似器」の一つの例として、3次元シーンのレンダリングを学習させてみました。小さなシーンですが、原理的にはより多くの変数や値域でも学習ができるはずです。十分な計算リソースがあれば。
このように自前で一から実装してみるのは、やはり理解に役立ちます。特にディープラーニング界隈では TensorFlow や PyTorch などのフレームワークが便利なので、中身をブラックボックスとして扱いがちだと思いますが、中身を理解するには作ってみるのが一番です。
このプロジェクトでは Rust を使いましたが、実際に非常に書きやすく感じました。 Python のように動的型だと何か機能を追加するたびに他の何かが壊れるのが普通ですが、 Rust ではそのようなバグの多くがコンパイル時に検出されます。これは生産性に大きく寄与しました。実行速度については言わずもがなです。

脚注

そもそも Typst に手を出した理由が、このような長いドキュメントを管理しやすい形で書く方法を探していたことなのですが、その結果についてはリンク先に記事に書きました。 ↩︎
数学的にはヘヴィサイドの階段関数に似ているが、 $x=0$ の時 0.5 という値をとることが定義されている点が異なります。現実には信号の計算結果が厳密な0に一致することはほぼ皆無であり、違いを気にする必要はありません。 ↩︎
私が習ったときには合成関数の微分則と呼んでいましたが、英語では chain rule が一般的なようです。 ↩︎
実は活性化関数に三角関数を使えば表現できますが、これは $f(x,y) = sin((x + y)/\pi)$ というような関数を考えてみれば XOR に相当する関数を表現できることが分かります。 ↩︎
なお、球の大きさも少し違うように見えますが、これはレイトレーシングの光線の方向の計算方法の違いによるもので、ちょっとしたバグがあると思います。 ↩︎