🚚

Rust で自動微分ライブラリ作ってみたその2 ~応用編~

2023/07/30に公開

Rust

前回は自動微分ライブラリを一から書き上げてみました。前提知識がほぼない状態で始めましたが、まずはその後いくらか調べた結果をまとめておきます。

コンピュータにおける微分の種類

コンピュータで行う微分とは、主に次の三つのどれかに分類できます。

記号微分/数式微分 (Symbolic differentiation) - 人間が紙の上でやるように、数式の変形で新たな式(導関数)を導く方法です。閉じた形式の式が求まるので計算は正確ですが、一つの式に多数の変数が現れる場合、それぞれに対して求めなければいけないので、効率は悪いです。代表的な製品には Python の sympy ライブラリ、 Matlab の Symbolic Math Toolbox、Maxima 、Wolfram Alpha などがあります。
自動微分 (Automatic differentiation) - 本記事の主題です。計算グラフをツリー構造で記憶しておき、ノードを辿ることで値や微分係数を計算します。数式微分に似ていますが、違いは計算グラフをツリーとして記憶しておくことと、具体的な値を代入して直接結果を求めることです。大きな利点として、多数の変数が式に出現する場合でも効率的に計算できる点があり、このような計算方法を Reverse mode automatic differentiation またはディープラーニング界隈ではバックプロパゲーションと呼びます。 PyTorch や TensorFlow では一部として組み込まれています。
数値微分 (Numerical differentiation) - 実際に少しだけ変数を動かしてみて、関数の値がどれだけ変わるかを見て微分係数を求める方法です。直感的でライブラリなどを使わなくても簡単にできるのが利点ですが、正確性は低く、効率も悪いです^[1]。主に上記二つの実装が合っているかを確かめるクロスチェックのために使われます。

さらなる最適化

前回は参照バージョン Term<'a> と参照カウンタバージョン RcTerm を実装しましたが、これらはヒープ上にノードをばらばらに確保するので効率は良いとは言えません。グラフに属するノードのメモリを一続きのメモリにしたほうがキャッシュヒット率は上がります。このようなメモリ確保戦略をアリーナと言ったりしますが、自動微分界隈では Tape と呼ばれているらしいです^[2]。

まずはこの Tape をデータ構造化します。単純な動的配列にノードを配置します。ここで RefCell が出てくるのはあまり美しくありませんが、このノードのリストへの参照は多数出現するのでやむを得ないです。

#[derive(Default, Debug)]
pub struct Tape {
    nodes: RefCell<Vec<TapeNode>>,
}

#[derive(Clone, Debug)]
struct TapeNode {
    name: String,
    value: TapeValue,
    data: f64,
    grad: f64,
}

TapeValue の中身は次のような列挙型です。ポインタの代わりに配列のインデックスを使った相対アドレッシング^[3]で親を指定します。

#[derive(Clone, Debug)]
struct UnaryFnPayload {
    term: u32,
    f: fn(f64) -> f64,
    grad: fn(f64) -> f64,
}

#[derive(Clone, Debug)]
enum TapeValue {
    Value(f64),
    Add(u32, u32),
    Sub(u32, u32),
    Mul(u32, u32),
    Div(u32, u32),
    Neg(u32),
    UnaryFn(UnaryFnPayload),
}

ひとたび Tape をこのように定義すれば、ノードを追加した時には単純にそのインデックスを返すことでノードを参照する「ハンドル」となります。

#[derive(Copy, Clone)]
pub struct TapeTerm<'a> {
    tape: &'a Tape,
    idx: u32,
}

あとの使い方は最初に Tape オブジェクトを初期化するだけで Term や RcTerm と大きく変わりません。

    let tape = Tape::new();
    let a = tape.term("a", 123.);
    let b = tape.term("b", 321.);
    let c = tape.term("c", 42.);
    let ab = a + b;
    let abc = ab * c;
    println!("a + b = {}", ab.eval());
    println!("(a + b) * c = {}", abc.eval());
    let ab_a = ab.derive(&a);
    println!("d(a + b) / da = {}", ab_a);
    let abc_a = abc.derive(&a);
    println!("d((a + b) * c) / da = {}", abc_a);
    let abc_b = abc.derive(&b);
    println!("d((a + b) * c) / db = {}", abc_b);
    let abc_c = abc.derive(&c);
    println!("d((a + b) * c) / dc = {}", abc_c);

ただ、 Rust の場合は Tape を使うことによる大きなメリットが一つあります。それは「ハンドル」を単なる整数のインデックスにできる^[4]ので、 Copy トレイトを実装できることです。これによって式の中でいちいち全ての変数に参照 & をつけなくてもよくなりますし、より重要なのは一時変数をローカル変数にバインドしなくても済むことです。これで次のような多数の変数が出現する式が一行で書けます。

let gaussian = scale * (-(x_mu * x_mu) / sigma / sigma).apply("exp", f64::exp, f64::exp);

自動微分の応用先

自動微分の利点は、多数の変数があっても全てに関する微分係数を一度に求めることができることです。それも、計算グラフの木構造を辿りながら行うので、重複した計算はなく、数式微分でいえば因数分解された状態で行うので、計算にも無駄がありません。

主な応用先は、もちろんディープラーニングですが、それ以外にもいろいろなことに使えます。
実装は前回と同じリポジトリの examples フォルダにあります。

https://github.com/msakuta/rustograd

関数フィッティング

ソース

ガウス分布を含んでいると考えられるデータが与えられたときのことを考えます。分布の平均や標準偏差は未知であると想定します。最小二乗法によってこれらのパラメータ $\mu, \sigma, s$ を推定することができます。

f(x; \mu, \sigma, s) = s \exp \left(-\frac{(x - \mu)^2}{\sigma^2} \right)

最小二乗法を適用するためには、次のような誤差関数を定義する必要があります。
ここで $x_i, y_i$ は $i$ 番目のサンプルです。

L = \sum_i (f(x_i) - y_i)^2

一つ一つ偏微分係数を手で計算していってもいいのですが、面倒です(このレベルでは大したことないですが、この手法を拡張していくにつれすぐに手に負えなくなります)。偏微分係数が求まれば下記のように学習速度パラメータ $\alpha$ を使って再急降下法を使って最適解を探せます。

\begin{align*} \mu &\leftarrow \mu - \alpha \frac{\partial L}{\partial \mu} \\ \sigma &\leftarrow \sigma - \alpha \frac{\partial L}{\partial \sigma} \\ s &\leftarrow s - \alpha \frac{\partial L}{\partial s} \end{align*}

ここで自動微分の出番です。自動微分があれば下記のように計算グラフを構築して loss.backprop() を呼び出すだけです。

    let x = tape.term("x", 0.);
    let mu = tape.term("mu", 0.);
    let sigma = tape.term("sigma", 1.);
    let scale = tape.term("scale", 1.);
    let x_mu = x - mu;
    let gaussian = scale * (-(x_mu * x_mu) / sigma / sigma).apply("exp", f64::exp, f64::exp);
    let sample_y = tape.term("y", 0.);
    let diff = gaussian - sample_y;
    let loss = diff * diff;

最適化ループはクリエイティブになれる部分ですが、例えば次のような単純な更新ルールでも良いです。

    let optimize = |mu: &mut f64, sigma: &mut f64, scale: &mut f64| {
        model.mu.set(*mu).unwrap();
        model.sigma.set(*sigma).unwrap();
        model.scale.set(*scale).unwrap();
        for (&xval, &sample_y) in samples.iter().zip(truth_data.iter()) {
            model.x.set(xval).unwrap();
            model.sample_y.set(sample_y).unwrap();
            model.loss.eval();
            model.loss.backprop();
            *mu -= RATE * model.mu.grad();
            *sigma -= RATE * model.sigma.grad();
            *scale -= RATE * model.scale.grad();
        }
    };

次に示すアニメーションは、実際に自動微分を使って適当に決めた初期値 init_y が truth_y に収束していく様子を示しています。

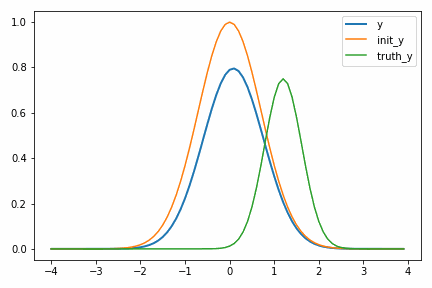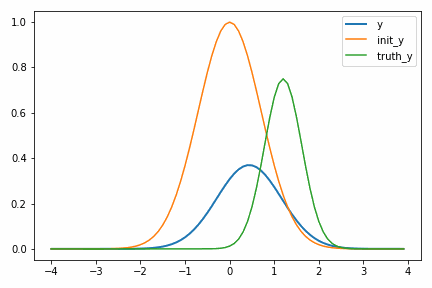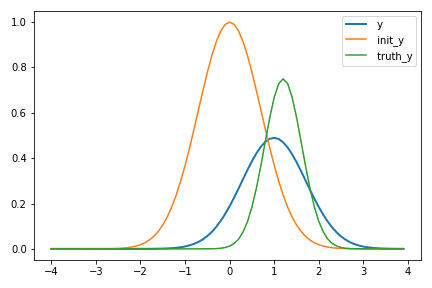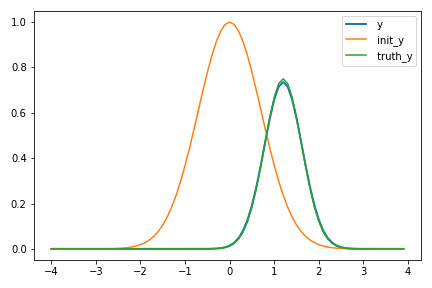
一度スケールパラメータ s が小さくなるのが面白いですが、これは初期値の付近では関数の値が小さく、スケールを落とした方が誤差関数が小さくなるからだと考えられます。このような「回り道」は最適化ではよく見られるもので、最終的に収束するのであれば問題にはなりません。ただどうしても気になるのであればパラメータ $\mu$ だけを最初に最適化するなどの方法はあります。

計算グラフを描画すると次のようになります。

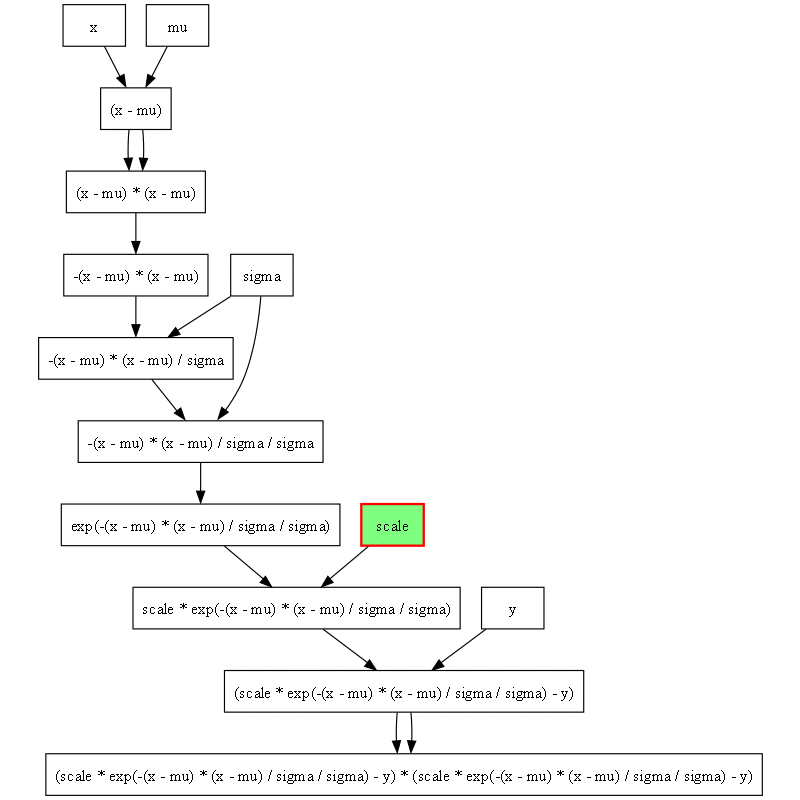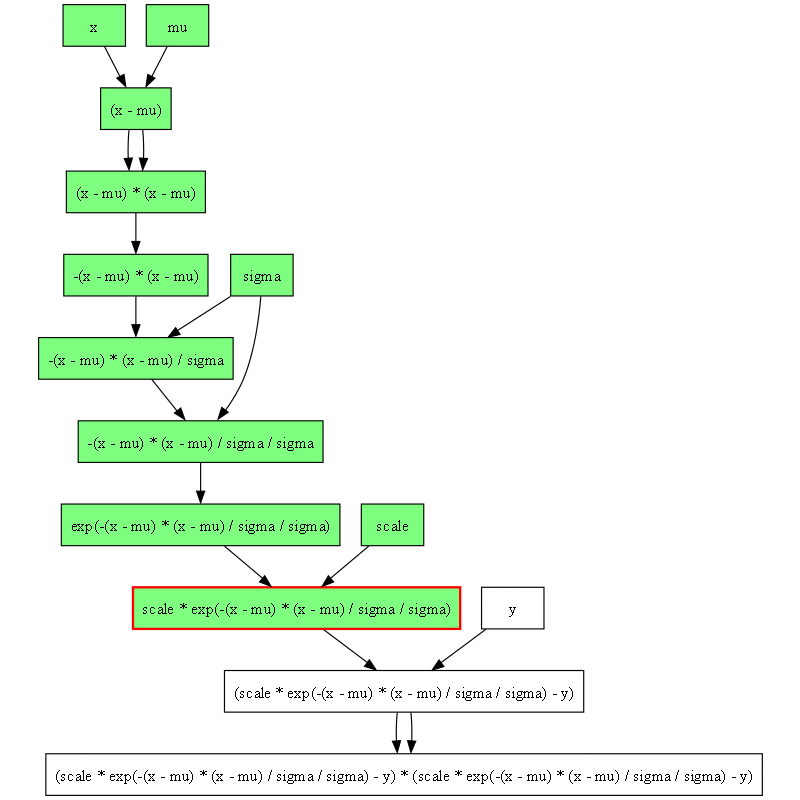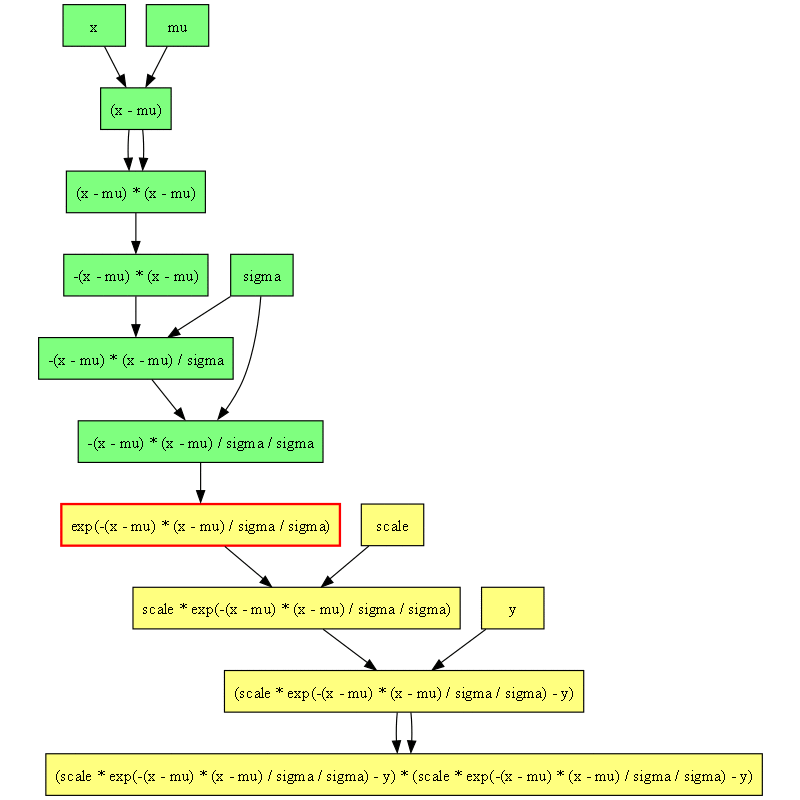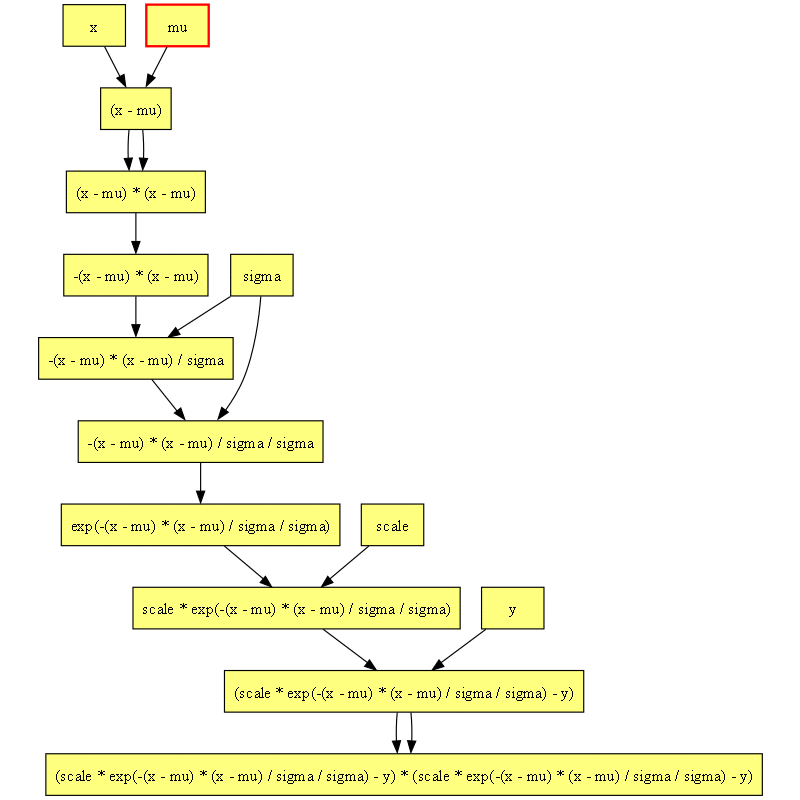
この例では次のような標本平均と標本分散を使って直接パラメータを推定できるので、それほど感慨がわかないかもしれません。しかし次のセクションからもう少し面白くなります。

\begin{align*} \mu &= \frac{1}{N}\sum_i x \\ \sigma &= \sqrt{\frac{1}{N - 1}\sum_i (x - \mu)^2} \end{align*}

ピーク分離

ソース

計測の世界でたびたび出現するのが、ピーク分離という問題です。関数フィッティングに似ていますが、複数のガウス分布を含み、主な目的は二つのピークそれぞれのパラメータを求めることです。

f(x; \mathbf{\mu}, \mathbf{\sigma}, \mathbf{s}) = \sum_k s_k \exp \left(-\frac{(x - \mu_k)^2}{\sigma_k^2} \right)

モデルは前セクションとよく似ていますが、ガウス分布が二つあるのでその部分はラムダで共通化しています。

    let x = tape.term("x", 0.);

    let gaussian = |i: i32| {
        let mu = tape.term(format!("mu{i}"), 0.);
        let sigma = tape.term(format!("sigma{i}"), 1.);
        let scale = tape.term(format!("scale{i}"), 1.);
        let x_mu = x - mu;
        let g = scale * (-(x_mu * x_mu) / sigma / sigma).apply("exp", f64::exp, f64::exp);
        (mu, sigma, scale, g)
    };

    let (mu0, sigma0, scale0, g0) = gaussian(0);
    let (mu1, sigma1, scale1, g1) = gaussian(1);
    let y = g0 + g1;

    let sample_y = tape.term("y", 0.);
    let diff = y - sample_y;
    let loss = diff * diff;

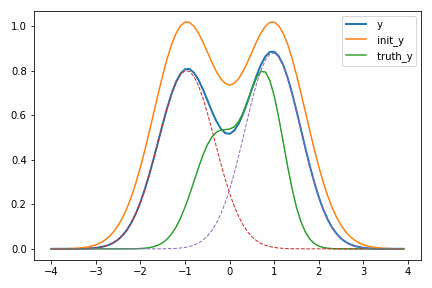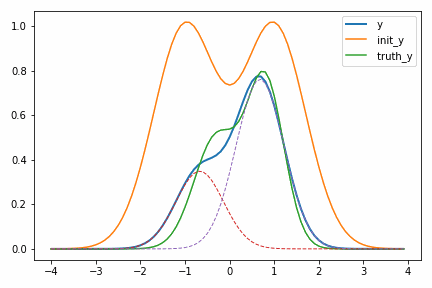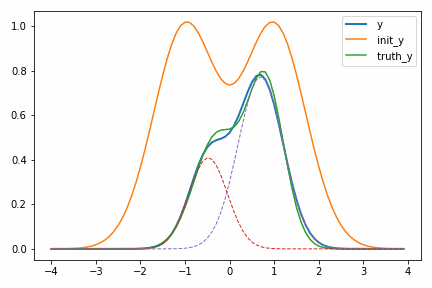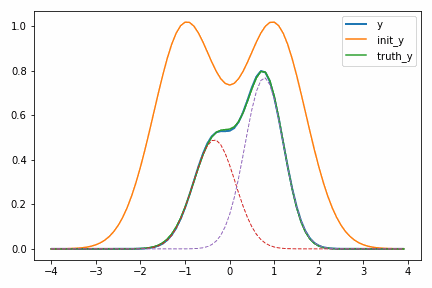
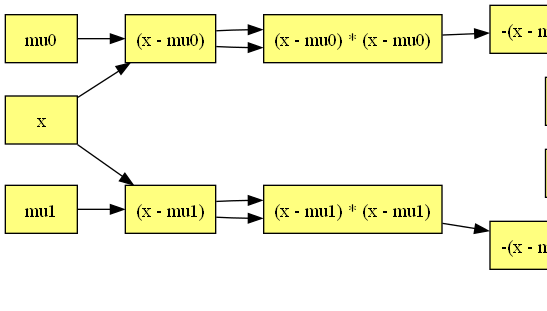
計算グラフはここまで来ると複雑すぎて手で偏微分を計算しようという意欲も湧いてきません。

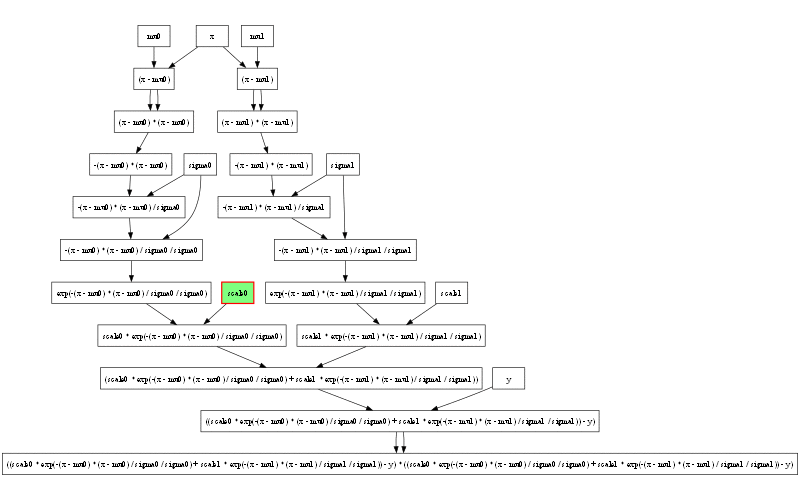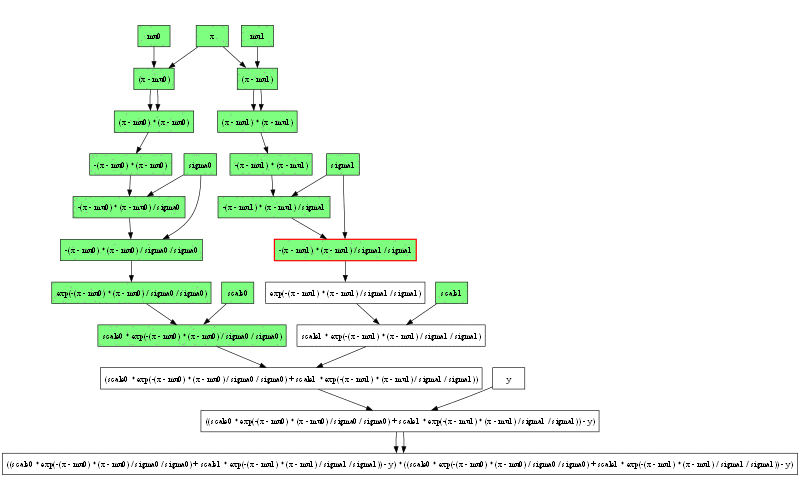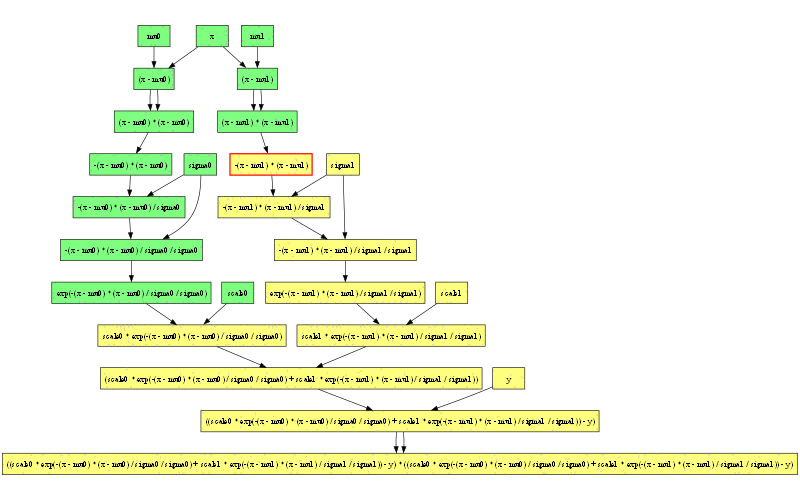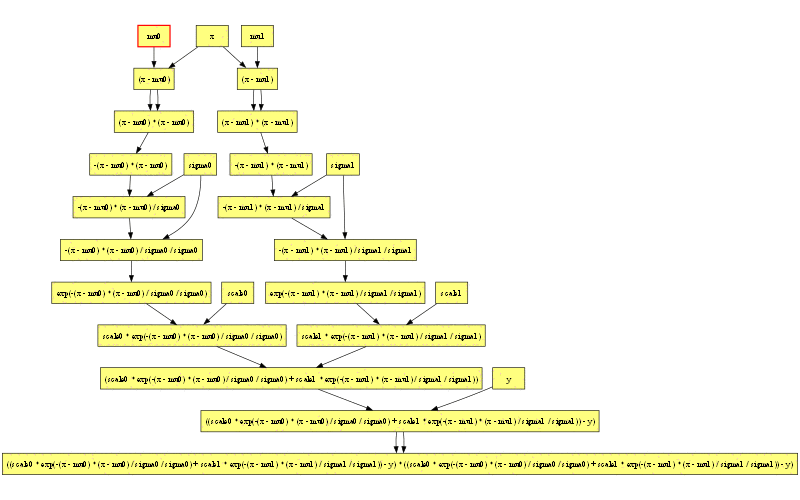
計算グラフの左端には注目する価値があります。2つのガウス分布の式で $x$ が共通であるため、グラフ上では共通祖先のノードとして出現します。また (x - mu0) から子ノードへの矢印が2重になっているのも面白いところです。これは2変数関数をまだサポートしていないので pow が実装できないためです。

なお、このような問題では初期値の設定が重要になります。真のピーク位置は次のように 0.8 と -0.3 ですが、初期値を 1.0 と 2.0 から始めてしまうとどうなるでしょうか。

    fn truth(x: f64) -> f64 {
        0.75 * (-(x - 0.8).powf(2.) / 0.35).exp() + 0.5 * (-(x + 0.3).powf(2.) / 0.5).exp()
    }

次のように局所解に落ち込んでしまいます。

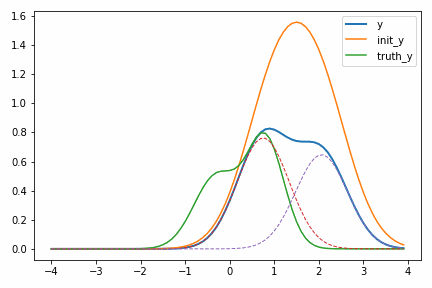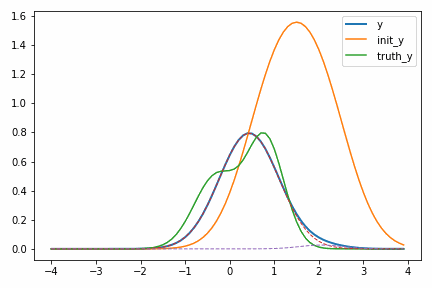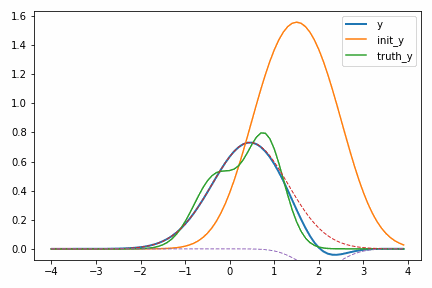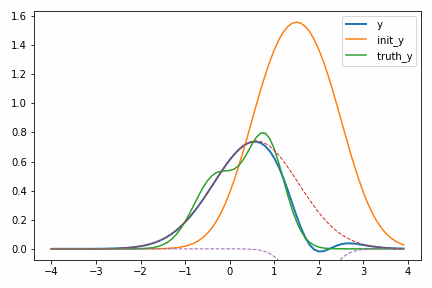
これを避けるための手法は様々ありますが、ここでは最も簡単なのは初期値のガウス分布で真のガウス分布を挟み込むようにすることです。三つ以上のガウス分布が混ざってきたときはさらに工夫する必要があります。

まとめ

本日は自動微分でできることの一端として関数フィッティングとピーク分離を紹介しました。ディープラーニングも一種の最適化問題なので、自動微分を使った最適化という問題の枠組みに当てはまりますが、それ以外にもいろいろ応用できそうだと思います。

個人的には自分で自動微分ライブラリを一度実装してみることをお勧めしたいと思います。木構造と再帰呼び出しができればそれほど難しくないですし、 Rust でなくても構いません。自分で実装することで見えてくる知見は、ただライブラリを使うだけよりもはるかに大きいと思います。

実際、自動微分の実装はある種の練習問題のように扱われているらしく、 GitHub で "autograd" を検索したり、Qiita で "自動微分" を検索すると死ぬほどヒットします。

脚注

非常に小さな値の差を複雑な計算に通したとき、結果の誤差は浮動小数点の性質から相対的に大きくなります。しかし、差分を大きくしすぎると真の微分係数からの乖離が大きくなります。 ↩︎
厳密には微分係数は別の配列にして返すことで複数の関数で共有できるようにするのを Tape と呼ぶようです。 rustograd は Define-and-run 設計であり、繰り返し backprop() を呼ぶことでテンソルのサポートの代わりにしているので、微分係数 grad のバッファは TapeNode の一部にしてメモリアロケーションを減らしています。 ↩︎
ここでいう相対アドレッシングとは、このノードからの相対アドレスではなく(それでも動きますが)この配列の先頭からのアドレスという意味です。 usize は 64bit 環境では大きすぎるので u32 にしてあります。 ↩︎
これは Rust の借用チェッカーを回避する代表的な手段で、メモリアリーナのようなデータ構造の実装では多用されます。ここでは動的配列の増長に伴うリアロケーションが起こっても有効な参照であり続けるためにインデックスで参照しています。配列の大きさを超えるインデックスでアクセスしようとすると実行時エラーになるので、生の参照なら借用チェッカーがコンパイル時にチェックできることを実行時にしているわけです。「回避できるなら借用チェッカーを言語に実装する意味はあるのか」と Rust の言語設計を批判する人もいますが、借用チェッカーが防いでいるのは未定義動作であり、範囲外アクセスは未定義動作ではありません。 ↩︎

コンピュータにおける微分の種類

さらなる最適化

自動微分の応用先

関数フィッティング

ピーク分離

まとめ

Discussion