〰️
「FFT(高速フーリエ変換)を完全に理解した」になるまで 3(実装編)
アプリを作ってフーリエ変換を視覚的に確認してみる
- ブラウザ上で動作するwebアプリを作ってみました。
こちらより確認できます。
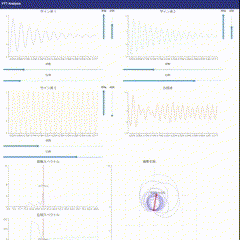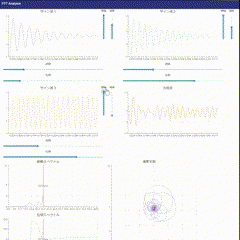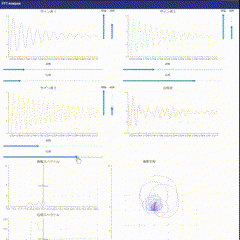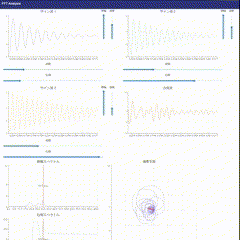
アプリの解説
- サイン波の生成: 3種類の振動をグラフ化します。振幅、周期、減衰、位相の4つのパラメータを変更できます。
- 合成波の生成: 単振動を合成しグラフ化成します。
- 周波数軸グラフの生成: FFTを実装し振幅と位相をグラフ化します。
- 複素平面の視覚化: 指定した周波数でのDFTの結果を複素平面上にグラフ化します。
実装について
プログラム全体(React-TypeScriptで実装しています。)
import React, { useState, useEffect, PureComponent, useMemo } from "react";
import { AppBar, Toolbar, Typography, Grid, Slider, Box } from "@mui/material";
import { styled } from "@mui/material/styles";
import { SliderProps } from "@mui/material/Slider";
import {
LineChart,
Line,
CartesianGrid,
XAxis,
YAxis,
Tooltip,
ReferenceLine,
ResponsiveContainer,
} from "recharts";
// FFTアルゴリズムの実装(data点数が2のべき乗であることが前提)
function fft(data: Complex[]): Complex[] {
// データ内の点の総数N
const N = data.length;
// データが1点の場合、再帰を終了する
if (N <= 1) return data;
// データを偶数インデックスと奇数インデックスの要素に再帰的に分割
const half = N / 2;
const even = fft(data.filter((_, i) => i % 2 === 0));
const odd = fft(data.filter((_, i) => i % 2 !== 0));
// FFTの計算における負の回転因子を事前計算
const a = -2 * Math.PI;
// FFT結果を保持するための配列を初期化
let results = new Array<Complex>(N);
// 結果の前半部分のために偶数と奇数部分を組み合わせる処理を行うループ
for (let k = 0; k < half; k++) {
// k番目の回転因子 (e^(2πi*k/N)) を計算
const exp: Complex = {
r: Math.cos((a * k) / N),
i: Math.sin((a * k) / N),
};
// 奇数部FFT結果のk番目の要素に回転因子を適用
let temp: Complex = {
r: exp.r * odd[k].r - exp.i * odd[k].i,
i: exp.i * odd[k].r + exp.r * odd[k].i,
};
// 偶数部FFT結果と回転因子を適用した奇数部FFT結果を組み合わせる
results[k] = {
r: even[k].r + temp.r,
i: even[k].i + temp.i,
};
// FFT結果の後半部分を偶数部FFT結果から回転因子を適用した奇数部FFT結果を引いて計算
results[k + half] = {
r: even[k].r - temp.r,
i: even[k].i - temp.i,
};
}
// 結果として得られたFFTの配列を返す
return results;
}
// 特定の周波数に対するDFT計算関数
function calculateDFTForFrequency(
data: Complex[],
targetFrequency: number,
numPoints: number,
samplingRate: number
): Complex[] {
// DFT結果を格納する配列を初期化
const dftResults = [];
// 周波数をサンプルレートで正規化するための定数(ラジアン単位)
const twoPi = 2 * Math.PI;
const freqRad = (twoPi * targetFrequency) / samplingRate;
// データセットの各点に対してDFTの計算を行うループ
for (let n = 0; n < numPoints; n++) {
// 総和計算用の実部と虚部を初期化
let realPart = 0;
let imagPart = 0;
// この周波数とサンプルインデックスにおける角度を計算
const angle = freqRad * n;
// 実部と虚部の値を計算して総和
realPart = data[n].r * Math.cos(angle) - data[n].i * Math.sin(angle);
imagPart = data[n].i * Math.cos(angle) + data[n].r * Math.sin(angle);
// 計算された複素数をDFT結果配列に追加
dftResults.push({ r: realPart, i: imagPart });
}
// 計算されたDFT結果を返す
return dftResults;
}
const generateSineWave = (
numPoints: number,
freq: number,
amp: number,
decay: number,
phase: number
): Complex[] => {
return Array.from({ length: numPoints }, (_, index) => {
const angle =
(index / numPoints) * freq * Math.PI * 2 + (phase * Math.PI) / 180;
const amplitude = Math.sin(angle) * amp * Math.exp(-decay * index);
return { r: amplitude, i: 0 };
});
};
function formatFrequency(frequency: number): string {
return frequency.toFixed(1);
}
function App() {
const [frequencyRange, setFrequencyRange] = useState([0, 100]);
const [amp1, setAmp1] = useState<number>(5);
const [amp2, setAmp2] = useState<number>(5);
const [amp3, setAmp3] = useState<number>(5);
const [decay1, setDecay1] = useState<number>(0.003);
const [decay2, setDecay2] = useState<number>(0.005);
const [decay3, setDecay3] = useState<number>(0.001);
const [freq1, setFreq1] = useState<number>(17);
const [freq2, setFreq2] = useState<number>(23);
const [freq3, setFreq3] = useState<number>(31);
const [phase1, setPhase1] = useState<number>(-120);
const [phase2, setPhase2] = useState<number>(77);
const [phase3, setPhase3] = useState<number>(0);
const [selectedFrequency, setSelectedFrequency] = useState(33.201);
const [dftDataForChart, setDftDataForChart] = useState<Complex[]>([]);
const [centroid, setCentroid] = useState({ r: 0, i: 0 });
const numPoints = 512;
const samplingRate = 1000;
const freqStep = parseFloat((samplingRate / numPoints).toFixed(3));
const sineWave1 = generateSineWave(numPoints, freq1, amp1, decay1, phase1);
const sineWave2 = generateSineWave(numPoints, freq2, amp2, decay2, phase2);
const sineWave3 = generateSineWave(numPoints, freq3, amp3, decay3, phase3);
const compositeWave = sineWave1.map((point, index) => {
return {
r: point.r + sineWave2[index].r + sineWave3[index].r,
i: point.i + sineWave2[index].i + sineWave3[index].i,
};
});
const timeAxis = Array.from(
{ length: numPoints },
(_, i) => i / samplingRate
);
const generateChartData = (waveData: Complex[], timeAxis: number[]) =>
waveData.map((point: Complex, index: number) => ({
time: timeAxis[index],
value: point.r,
}));
const chartData1 = generateChartData(sineWave1, timeAxis);
const chartData2 = generateChartData(sineWave2, timeAxis);
const chartData3 = generateChartData(sineWave3, timeAxis);
const chartDataComposite = generateChartData(compositeWave, timeAxis);
const fftResults = fft(compositeWave);
const frequencyAxis = Array.from(
{ length: numPoints / 2 },
(_, i) => (i * samplingRate) / numPoints
);
const amplitudeSpectrum = fftResults.map((c) =>
Math.sqrt(c.r ** 2 + c.i ** 2)
);
const amplitudeSpectrumData = amplitudeSpectrum
.slice(0, numPoints / 2)
.map((amp, index) => ({
frequency: frequencyAxis[index],
amp: (amp * 2) / numPoints,
}));
const phaseSpectrum = fftResults.map((c) => {
let phase = (Math.atan2(c.i, c.r) * 180) / Math.PI + 90;
if (phase > 180) phase += -360;
return phase;
});
const phaseSpectrumData = phaseSpectrum
.slice(0, numPoints / 2)
.map((phase, index) => ({
frequency: frequencyAxis[index],
phase: phase,
}));
useEffect(() => {
const dftResults = calculateDFTForFrequency(
compositeWave,
selectedFrequency,
numPoints,
samplingRate
);
setDftDataForChart(dftResults);
const total = dftResults.reduce(
(acc, point) => ({ r: acc.r + point.r, i: acc.i + point.i }),
{ r: 0, i: 0 }
);
setCentroid({
r: (total.r / dftResults.length) * 2,
i: (total.i / dftResults.length) * 2,
});
}, [
selectedFrequency,
numPoints,
samplingRate,
freq1,
freq2,
freq3,
amp1,
amp2,
amp3,
decay1,
decay2,
decay3,
phase1,
phase2,
phase3,
]);
return (
<>
<StyledAppBar position="static">
<Toolbar>
<StyledTypography variant="h6">FFT Analysis</StyledTypography>
</Toolbar>
</StyledAppBar>
<Grid container spacing={2}>
{/* 各サイン波のグラフとスライダー */}
<Grid item xs={9} md={5}>
<WaveChart data={chartData1} color="#8884d8" title="サイン波 1" />
<LabeledHorizonSlider
label="周期"
value={freq1}
onChange={(e, val) => typeof val === "number" && setFreq1(val)}
min={1.0}
max={50.0}
/>
<LabeledHorizonSlider
label="位相"
value={phase1}
onChange={(e, val) => typeof val === "number" && setPhase1(val)}
min={-180}
max={180}
step={1}
/>
</Grid>
<Grid item xs={1} md={0.4}>
<LabeledVerticalSlider
label="振幅"
value={amp1}
onChange={(e, val) => typeof val === "number" && setAmp1(val)}
orientation="vertical"
min={0}
max={5}
step={0.1}
/>
</Grid>
<Grid item xs={1} md={0.4}>
<LabeledVerticalSlider
label="減衰"
value={decay1}
onChange={(e, val) => typeof val === "number" && setDecay1(val)}
orientation="vertical"
min={0}
max={0.01}
step={0.001}
/>
</Grid>
<Grid item xs={9} md={5}>
<WaveChart data={chartData2} color="#82ca9d" title="サイン波 2" />
<LabeledHorizonSlider
label="周期"
value={freq2}
onChange={(e, val) => typeof val === "number" && setFreq2(val)}
min={1.0}
max={50.0}
/>
<LabeledHorizonSlider
label="位相"
value={phase2}
onChange={(e, val) => typeof val === "number" && setPhase2(val)}
min={-180}
max={180}
step={1}
/>
</Grid>
<Grid item xs={1} md={0.4}>
<LabeledVerticalSlider
label="振幅"
value={amp2}
onChange={(e, val) => typeof val === "number" && setAmp2(val)}
orientation="vertical"
min={0}
max={5}
step={0.1}
/>
</Grid>
<Grid item xs={1} md={0.4}>
<LabeledVerticalSlider
label="減衰"
value={decay2}
onChange={(e, val) => typeof val === "number" && setDecay2(val)}
orientation="vertical"
min={0}
max={0.01}
step={0.001}
/>
</Grid>
<Grid item xs={9} md={5}>
<WaveChart data={chartData3} color="#ffc658" title="サイン波 3" />
<LabeledHorizonSlider
label="周期"
value={freq3}
onChange={(e, val) => typeof val === "number" && setFreq3(val)}
min={1.0}
max={50.0}
/>
<LabeledHorizonSlider
label="位相"
value={phase3}
onChange={(e, val) => typeof val === "number" && setPhase3(val)}
min={-180}
max={180}
step={1}
/>
</Grid>
<Grid item xs={1} md={0.4}>
<LabeledVerticalSlider
label="振幅"
value={amp3}
onChange={(e, val) => typeof val === "number" && setAmp3(val)}
orientation="vertical"
min={0}
max={5}
step={0.1}
/>
</Grid>
<Grid item xs={1} md={0.4}>
<LabeledVerticalSlider
label="減衰"
value={decay3}
onChange={(e, val) => typeof val === "number" && setDecay3(val)}
orientation="vertical"
min={0}
max={0.01}
step={0.001}
/>
</Grid>
{/* 合成波のグラフ */}
<Grid item xs={9} md={5}>
{" "}
<CompositeChart
data={chartDataComposite}
color="#ff7300"
title="合成波"
/>
</Grid>
</Grid>
<Grid container spacing={2}>
{/* 振幅スペクトルのグラフ */}
<Grid item xs={12} md={5}>
<Grid>
<Box sx={{ width: "100%", height: "100%" }}>
<SpectrumChart
title="振幅スペクトル"
data={amplitudeSpectrumData}
frequencyRange={frequencyRange}
color="#8884d8"
dataKey="amp"
selectedFrequency={selectedFrequency}
dominMinY={0}
dominMaxY={10}
/>
</Box>
</Grid>
{/* 位相スペクトルのグラフ */}
<Grid>
<Box sx={{ width: "100%", height: "100%" }}>
<SpectrumChart
title="位相スペクトル"
data={phaseSpectrumData}
frequencyRange={frequencyRange}
color="#82ca9d"
dataKey="phase"
selectedFrequency={selectedFrequency}
dominMinY={-200}
dominMaxY={200}
/>
</Box>
</Grid>
</Grid>
<Grid item xs={12} md={5}>
<ComplexPlaneChart
title="複素平面"
data={dftDataForChart}
centroid={centroid}
/>
</Grid>
<Grid container spacing={2}>
<Grid item xs={12} md={12}>
<Typography align="center" marginTop={3}>
選択周波数: {selectedFrequency} Hz
</Typography>
</Grid>
<Grid item xs={10} md={5}>
<LabeledHorizonSlider
label="周波数表示範囲"
value={frequencyRange}
onChange={(e, val) => setFrequencyRange(val as number[])}
valueLabelDisplay="auto"
min={0}
max={250} // ナイキスト周波数まで
/>
</Grid>
<Grid item xs={10} md={5}>
<LabeledHorizonSlider
label="表示周波数選択"
value={selectedFrequency}
onChange={(e, val) => setSelectedFrequency(val as number)}
min={0}
max={numPoints / 4 - 1}
step={freqStep}
/>
</Grid>
</Grid>
</Grid>
<StyledAppBar position="static">
<Toolbar>
<StyledTypography>Copyright (c) 2023 mass</StyledTypography>
</Toolbar>
</StyledAppBar>
</>
);
}
export default App;
// スタイリング
const StyledAppBar = styled(AppBar)({
background: "#2c387e",
boxShadow: "none",
borderBottom: "1px solid rgba(255, 255, 255, 0.12)",
});
const StyledTypography = styled(Typography)({
fontWeight: 500,
color: "#FFFFFF",
});
const VerticalSlider = styled(Slider)(({ theme }) => ({
"& .MuiSlider-thumb": {
height: 10,
width: 10,
},
"& .MuiSlider-track": {
width: 2,
},
"& .MuiSlider-rail": {
width: 3,
},
height: 150,
marginTop: theme.spacing(1),
marginBottom: theme.spacing(1),
marginLeft: theme.spacing(0),
marginRight: theme.spacing(0),
}));
const LabeledVerticalSlider = ({
label,
...sliderProps
}: LabeledVerticalSliderProps) => {
return (
<Box sx={{ width: "100%", height: "100%", textAlign: "center" }}>
<Typography gutterBottom>{label}</Typography>
<VerticalSlider {...sliderProps} />
</Box>
);
};
const HorizonSlider = styled(Slider)(({ theme }) => ({
"& .MuiSlider-thumb": {
height: 10,
width: 10,
},
"& .MuiSlider-track": {
height: 2,
},
"& .MuiSlider-rail": {
height: 3,
},
marginLeft: theme.spacing(4),
marginRight: theme.spacing(4),
}));
const LabeledHorizonSlider = ({
label,
...sliderProps
}: LabeledHorizonSliderProps) => {
return (
<Box sx={{ width: "100%", height: "15%", textAlign: "center" }}>
<Typography gutterBottom>{label}</Typography>
<HorizonSlider {...sliderProps} />
</Box>
);
};
// インターフェース
interface Complex {
r: number;
i: number;
}
interface WaveData {
time: number;
value: number;
}
interface ComplexPlaneChartProps {
data: Complex[];
centroid: Complex;
title: string;
}
interface LabeledVerticalSliderProps extends SliderProps {
label: string;
}
interface LabeledHorizonSliderProps extends SliderProps {
label: string;
}
interface CustomizedLabelProps {
x: number;
y: number;
stroke: string;
value: string;
}
class CustomizedLabel extends PureComponent<CustomizedLabelProps> {
render() {
const { x, y, stroke, value } = this.props;
return (
<text
x={x}
y={y}
dy={-10}
dx={10}
fill={stroke}
fontSize={16}
textAnchor="middle"
>
{value}
</text>
);
}
}
// グラフ
const WaveChart = ({
data,
color,
title,
}: {
data: WaveData[];
color: string;
title: string;
}) => {
return (
<Box>
<Typography variant="h6" align="center">
{title}
</Typography>
<ResponsiveContainer width="100%" height={300}>
<LineChart data={data}>
<CartesianGrid strokeDasharray="3 3" />
<XAxis dataKey="time" />
<YAxis domain={[-5, 5]} />
<Line type="monotone" dot={false} dataKey="value" stroke={color} />
</LineChart>
</ResponsiveContainer>
</Box>
);
};
const CompositeChart = ({
data,
color,
title,
}: {
data: WaveData[];
color: string;
title: string;
}) => {
return (
<Box>
<Typography variant="h6" align="center">
{title}
</Typography>
<ResponsiveContainer width="100%" height={300}>
<LineChart data={data}>
<CartesianGrid strokeDasharray="3 3" />
<XAxis dataKey="time" />
<YAxis domain={[-15, 15]} />
<Line type="monotone" dot={false} dataKey="value" stroke={color} />
</LineChart>
</ResponsiveContainer>
</Box>
);
};
const SpectrumChart = ({
title,
data,
frequencyRange,
color,
dataKey,
selectedFrequency,
dominMinY,
dominMaxY,
}: {
title: string;
data: Array<{ frequency: number; [key: string]: number | string }>;
frequencyRange: number[];
color: string;
dataKey: string;
selectedFrequency: number;
dominMinY: number;
dominMaxY: number;
}) => {
const filteredData = data.filter(
(item) =>
item.frequency >= frequencyRange[0] && item.frequency <= frequencyRange[1]
);
return (
<Box>
<Typography variant="h6" align="center">
{title}
</Typography>
<ResponsiveContainer width="100%" height={300}>
<LineChart data={filteredData}>
<CartesianGrid strokeDasharray="3 3" />
<XAxis
dataKey="frequency"
domain={[frequencyRange[0], frequencyRange[1]]}
type="number"
scale="linear"
tickFormatter={formatFrequency}
/>
<YAxis domain={[dominMinY, dominMaxY]} />
<Tooltip />
<ReferenceLine x={selectedFrequency} stroke="red" label="DFT freq" />
<Line type="monotone" dot={false} dataKey={dataKey} stroke={color} />
</LineChart>
</ResponsiveContainer>
</Box>
);
};
const ComplexPlaneChart: React.FC<ComplexPlaneChartProps> = ({
title,
data,
centroid,
}) => {
const chartData = data.map((point, index) => ({
x: point.r,
y: point.i,
index,
}));
const [width, height] = useWindowSize();
const chartSize = Math.min(600, width - 30);
return (
<Box width={chartSize} height={chartSize}>
<Typography variant="h6" align="center">
{title}
</Typography>
<ResponsiveContainer>
<LineChart>
{calcRefLines(-15, 15, 5).map((line) => (
<ReferenceLine key={line.key} x={line.value} stroke="lightgrey" />
))}
{calcRefLines(-15, 15, 5).map((line) => (
<ReferenceLine key={line.key} y={line.value} stroke="lightgrey" />
))}
<XAxis type="number" dataKey="y" name="Real" domain={[-15, 15]} />
<YAxis
type="number"
dataKey="x"
name="Imaginary"
domain={[-15, 15]}
/>
<Line
data={chartData}
type="monotone"
dot={false}
dataKey="x"
stroke="#8884d8"
/>
<Line
data={[
{ x: centroid.r.toFixed(2), y: centroid.i.toFixed(2) },
{ x: 0, y: 0 },
]}
dataKey="x"
stroke="red"
strokeWidth={4}
fill="red"
label={({ x, y, stroke, index }) =>
index === 0 ? (
<CustomizedLabel
x={x}
y={y}
stroke={stroke}
value={`X:${centroid.r.toFixed(2)}, Y:${centroid.i.toFixed(
2
)}`}
/>
) : (
<svg></svg>
)
}
/>
</LineChart>
</ResponsiveContainer>
</Box>
);
};
const calcRefLines = (min: number, max: number, step: number) => {
const lines = [];
for (let i = min; i <= max; i += step) {
lines.push({ key: `line-${i}`, value: i });
}
return lines;
};
function useWindowSize() {
const [size, setSize] = useState([window.innerWidth, window.innerHeight]);
useEffect(() => {
const handleResize = () => {
setSize([window.innerWidth, window.innerHeight]);
};
window.addEventListener("resize", handleResize);
return () => window.removeEventListener("resize", handleResize);
}, []);
return size;
}
再帰アルゴリズムについて
- 実装に当たり再帰的アルゴリズムを使用しています。
FFT関数の中でFFT関数を呼び出すことにより、再帰させます。
// FFTアルゴリズムの実装(data点数が2のべき乗であることが前提)
function fft(data: Complex[]): Complex[] {
// データ内の点の総数N
const N = data.length;
// データが1点の場合、再帰を終了する
if (N <= 1) return data;
// データを偶数インデックスと奇数インデックスの要素に再帰的に分割
const half = N / 2;
const even = fft(data.filter((_, i) => i % 2 === 0));
const odd = fft(data.filter((_, i) => i % 2 !== 0));
FFT関数を再帰する際にdataを偶数行、奇数行で分割し半分にしています。
条件分岐でdataが1以下になると、dataを返すことで繰り返しを終わり計算に入ります。
計算部分の実装
- ※Javascriptでは、デフォルトで虚数を扱えないため、sin・cos で計算しています。
// FFTの計算における負の回転因子を事前計算
const a = -2 * Math.PI;
// FFT結果を保持するための配列を初期化
let results = new Array() < Complex > N;
// 結果の前半部分のために偶数と奇数部分を組み合わせる処理を行うループ
for (let k = 0; k < half; k++) {
// k番目の回転因子 (e^(2πi*k/N)) を計算
const exp: Complex = {
r: Math.cos((a * k) / N),
i: Math.sin((a * k) / N),
};
// 奇数部FFT結果のk番目の要素に回転因子を適用
let temp: Complex = {
r: exp.r * odd[k].r - exp.i * odd[k].i,
i: exp.i * odd[k].r + exp.r * odd[k].i,
};
// 偶数部FFT結果と回転因子を適用した奇数部FFT結果を組み合わせる
results[k] = {
r: even[k].r + temp.r,
i: even[k].i + temp.i,
};
// FFT結果の後半部分を偶数部FFT結果から回転因子を適用した奇数部FFT結果を引いて計算
results[k + half] = {
r: even[k].r - temp.r,
i: even[k].i - temp.i,
};
}
// 結果として得られたFFTの配列を返す
return results;
}
表にして整理してみる
8点のデータで計算した例を表にまとめてみました。
- 表1:バタフライ演算(FFTの解説で用いられることの多い計算例)

入力に対し和と差を計算します。その際、差には回転因子
表1のように、収束するまで演算を繰り返し、最後にbitリバースを行い順番を並べ替えると出力がえられます。
-表2:再帰アルゴリズム(今回の実装)

入力を偶数部分と奇数部分を再帰的に分割していきます。
分割が最小単位になったら、それぞれに回転因子をかけて計算を繰り返します。
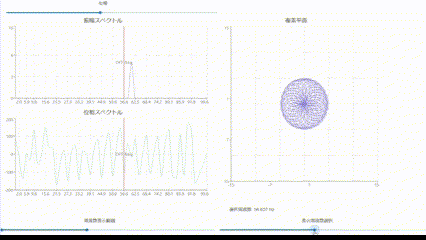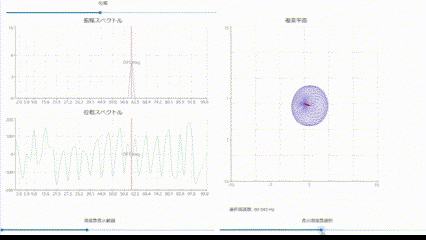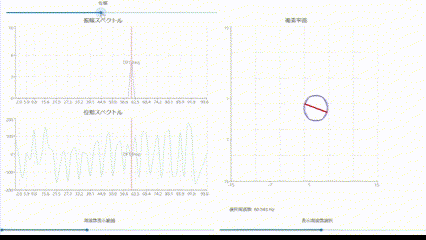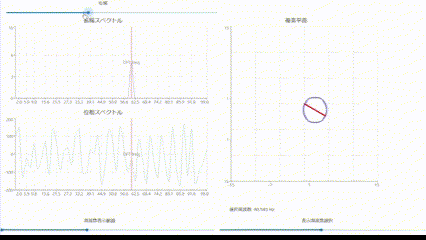
複素平面での表現について
- DFTで求められる結果を単一の周波数のみ抽出し複素平面上にグラフ化することで、
周波数毎に複素平面でどのように表現されるかを視覚化しました。
各周波数成分の振幅と位相の関係が直感的にわかると思います。
あとがき
今回FFTについて記事を書いてみましたが、アルゴリズム部分の最適化などまだちゃんと理解できていない部分も多いです。
計算式を眺めるよりはまずはやってみた方が分かりやすい分野だと思うので、言語(Excelでも)は何でもいいのでまず実装してみるといいかな、と思いました。
FFTだけであればPythonがコードも少ないし分かり易くていいですね。
pythonでの実装例
import numpy as np
def recursive_fft(x):
N = len(x)
if N <= 1:
return x
# 偶数インデックスと奇数インデックスに配列を分割
even = recursive_fft(x[0::2])
odd = recursive_fft(x[1::2])
# 一つの周期に対する回転因子を計算
twiddle_factors = np.exp(-2j * np.pi * np.arange(N) / N)
# FFTの結果を計算
return np.concatenate([even + twiddle_factors[:N // 2] * odd,
even - twiddle_factors[:N // 2] * odd])
# テストデータ(8点のサンプル)
x = np.random.random(8)
# 再帰的FFTを実行
fft_result = recursive_fft(x)
fft_result
ただ実装出来るだけでなく、ある程度中身も理解しておきたいと思いまとめてみました。
おわりに
機械設計やCAD、電子工作についてゆるくつぶやいています。
興味がある方は、ぜひX(旧 Twitter)をフォローしてください。
Discussion