「FFT(高速フーリエ変換)を完全に理解した」になるまで 1(概要編)

まえおき

FFT(高速フーリエ変換)について、数学的な視点から解説している記事は多いと思います。
私は機械系エンジニアとして務めているので、実用的な話やもう少し感覚的に理解できるような内容にまとめたいと思います。
また、FFTと関係ないですが、ダニング=クルーガー効果を知らない方は記事を読む前にチェックしておくことをお勧めします。

この記事のコンセプト

• 記事の前半では簡単に説明するために細かな説明は省きます。※正確な表現では無くなる場合もあります。
• 実装に入るまで数式は使わず、グラフと言葉で解説していきたいと考えています。(無理だったら・・・)
• 最初に概要や使い方、注意点などを、それ以降は実装しながら、計算方法や数式を解説したいと思います。
• 詳しく知りたい方はWikipediaや検索してください。私が説明するよりは正確に説明されている記事があると思います。

FFT(高速フーリエ変換)って?

振動を人(機械)が理解(処理)しやすい様に時間軸から周波数軸に変換する計算（アルゴリズム）です。
図1

図1の様な複数の単振動が足し合わさって出来た波形が、合成波（図2左）になります。
図2

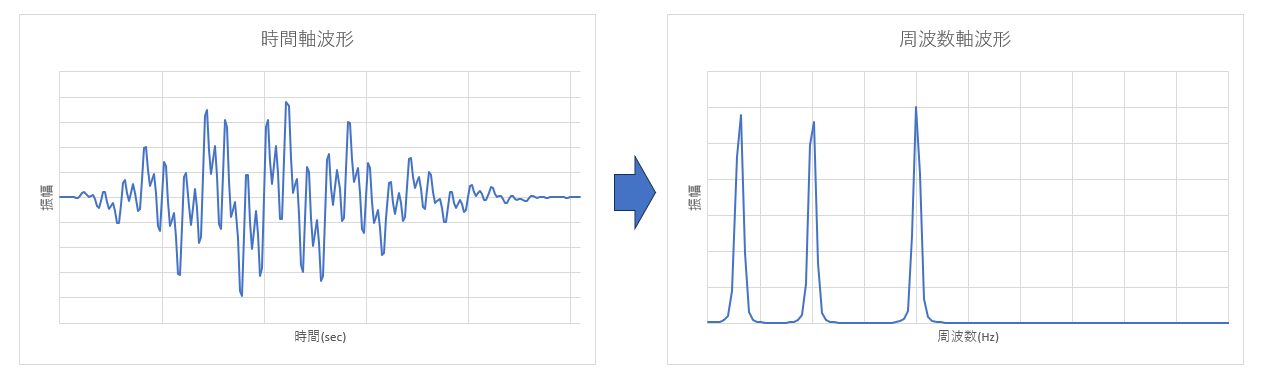
音や構造物の振動などは複雑な合成波となるため、時間軸波形からではどの様な特性か判別が難しいです。
その際にFFTを行い周波数軸の波形（図2右）に変換して確認します。

どんな時に使うの?

振動特性の確認、音声処理、画像処理などに使用されます。
その他にも、機械の異常検出、心電図の解析にも使われています。

どうやって使うの？

周波数軸の波形を比較して異常を見つけたり、特定の周波数のノイズを除去する等様々な使い方をします。

どんな分野に使われる?

• 機械の振動確認: 加速度センサーやレーザー計等を用いて機械の振動を測定し、FFTを行い特性を分析します。得られた特性が想定通りになっているか等を確認します。
• 音声データの分析: マイク等を用いて録音したデータにFFTを行い特性を分析します。
  オーディオ等で使われるイコライザーは見慣れているのではないでしょうか。
  低音を強くしたかったら低い周波数を強調したりしますよね。
• 画像処理: 画素値の変化を波としてとらえて、FFTを行いノイズの除去等を行います。画像のような2次元データは1次元ずつ処理を行うようです。ここら辺はあまり詳しくはないです。

使い方の例

下図は過去と現在の状態を比較するイメージ図

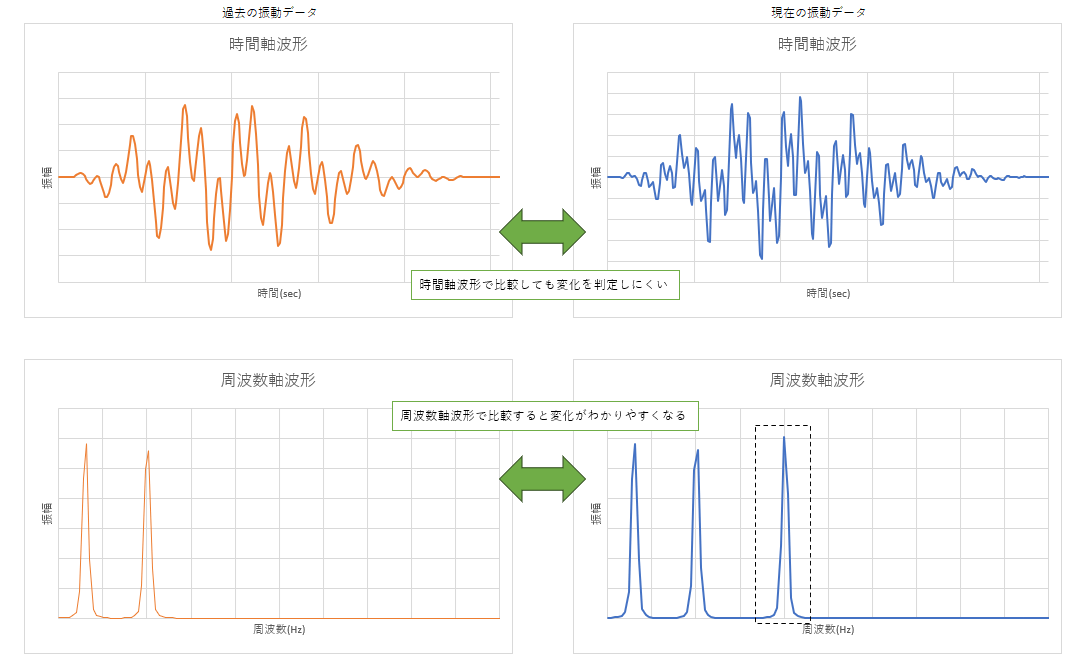
周波数軸に変換することで、どのような変化をしているのか分かりやすくなります。
このような変化から、異常が起こってないか?を推定したりします。

窓関数について

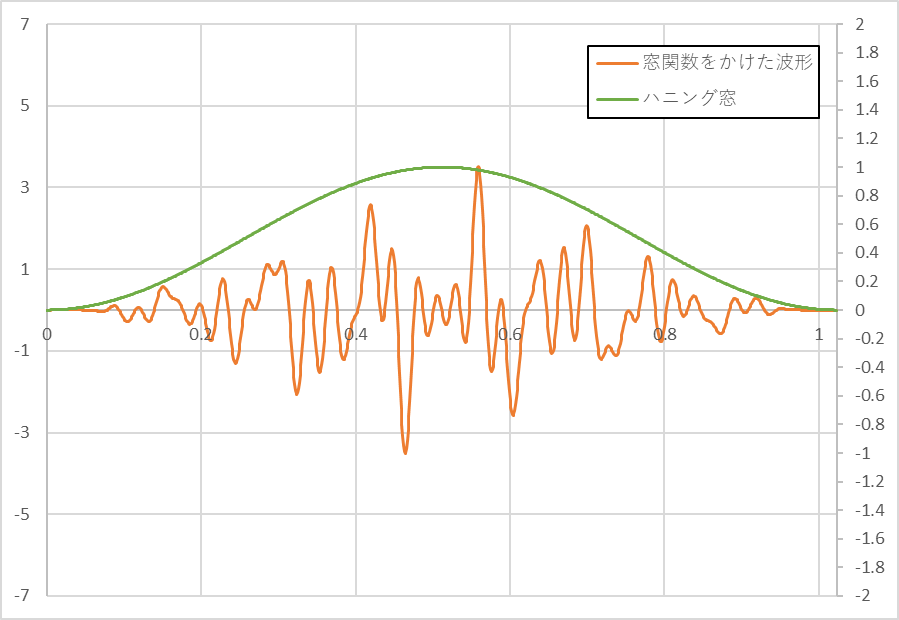
FFTを行う時の前処理として窓関数で振動波形を補正することが一般的です。
下図は窓関数での補正イメージ図です。

分析したい内容により適切な窓関数を選択する必要があります。

矩形窓

すべての領域で値が1となるため、波形が変化しませず、元の波形そのままとなります。

ハニング窓

0 から始まり、中央で最大値（1）に達し、再び0に戻るコサインカーブの形状の補正になります。
波形を切り取った場所による不連続を軽減し、周期性のある波形によく使われます。

何を使えばいいか?

周期的な振動に対しFFTを行う場合、ハニング窓の使用が一般的です。
矩形窓は、ハンマリング試験などの計測範囲内に振動の起点から収束までが含まれる場合に適しています。

注意点

• 矩形以外の窓関数を使用すると元の波形が変化することになります。それぞれの窓関数が波形にどのような影響を与えるかを理解することが大事です。

実際の測定

FFTを行う際は、事前に変換対象のデータを測定しておく必要があります。
例えば、機械の振動データを測定・分析する場合、以下の手順で行います。

測定～結果の確認までの流れ

1. 振動の測定: センサー等を用いてデータを収集

   • データの各測定点の間隔は一定である必要があります。
   • ハンマー等で加振する場合もあります。

   

2. 窓関数の適用: 収集したデータに窓関数などを適用
   

3. FFT: FFTを適用し、周波数成分を抽出
   

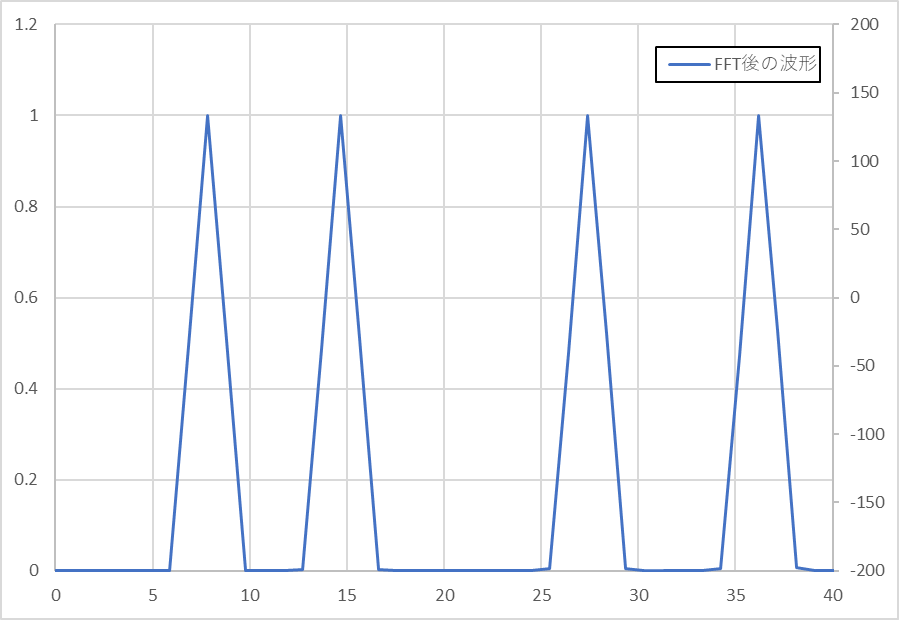
4. 結果の確認: FFTの結果を元に妥当性等の判断する

測定条件について

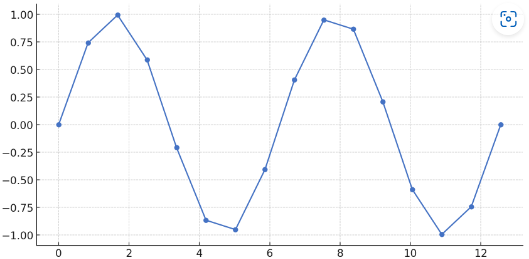
サンプリング間隔: 下図のように均一な間隔で取得
サンプリング点数: 2のべき乗で取得※測定後に2のべき乗になるよう切り取ってもOK。

また、測定器毎に適切な設定がされているかを確認する必要があります。
FFT機能付きの測定器を使用する場合、条件を満たすように設定されていることが多いと思います。

加振方法について

FFTはある入力(加振)に対し、出力(振動)を得たものを解釈しやすい形に変換する計算です。
出力を得るには、何かしらの入力が必要です。
一般的には、ハンマリングや振動試験機等が用いられます。
上記を使用し、インパルス加振やランダム加振などを行います。これにより、出力(振動)を得ます。

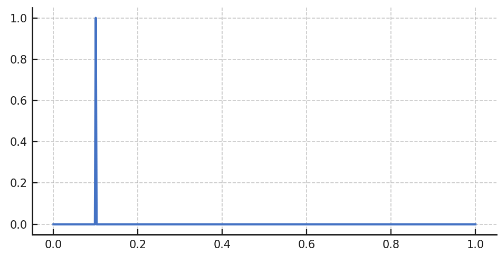
インパルス加振: インパルス加振は瞬間的(理想は0秒)に力を与えます。しかし、物体は弾性体のため、必ず力は時間をかけて与える事となります。

• 理想的なインパルス加振
  
• 現実の加振
  
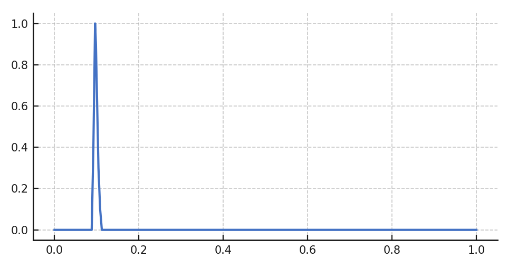
  力のかかる時間により物の動きに振動を抑える効果がかかってしまうため、試験をする時などは十分に気を付ける必要があります。

ランダム加振: ランダム加振は不規則に力を与えます。全周波数範囲にわたって一様なエネルギーとなるように加振する必要があります。

注意点

• FFTは周期的な振動の分析を前提とした計算方法です。
• インパルス加振などの非周期的な振動の場合、測定結果の解釈には特に注意が必要です。例えば、比較評価を行う場合には、測定/解析条件を一致させることが大事です。
• サンプリング間隔については、測定したい周波数に対応し、十分に短い時間とする必要があります。目安としては測定したい最大周波数の逆数の半分以下とする必要があります。

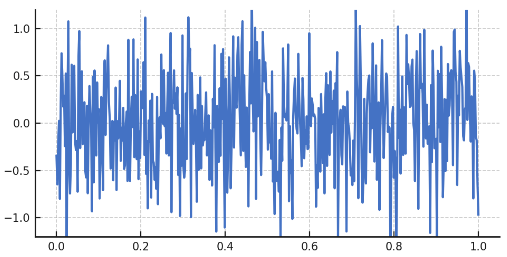
FFTの誤った使い方

FFTは誤った使い方をすると、思っていた答えが求められない可能性があります。
周期振動ではない波形をFFTする場合は特に注意が必要です。

誤ってハニング窓を適用した場合

タイミングにより FFT後の振幅の値が変化します。周期振動ではない場合は矩形窓を選択した方がよいです。

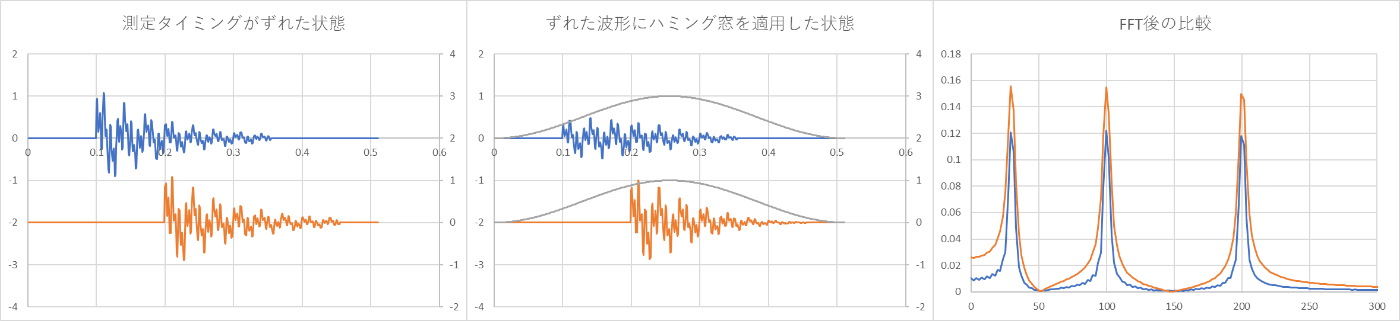
サンプリング点数が違う場合

周期的でない振動を比較したい場合は、比較前後で測定条件を同一にし、振動の起点から収束までが含む測定にすることが望ましいです。
また、振幅の絶対値も波形の切り取り方によって変わります。

※基本的に、FFT後に振幅の絶対値を求めるために、総サンプリング点数で割る事となります。そのため、サンプリング点数が多い(収束後の時間が長い)と、周波数軸での振幅の絶対値は小さくなります。

まとめ

FFTを行う際は色々なことに気を付けないと、得たい結果と違うものになってしまうことがあります。
色々な条件があり、一見複雑に見えるかもしれませんが、ひとつひとつの要素としては気を付けていれば難しいことではないので改めて理解しながら進めると今後のためになると思います。

FFTの「高速」について

FFT(高速フーリエ変換)は、DFT(離散フーリエ変換)の計算量を削減するアルゴリズムです。そのため、DFTと比べ高速に処理することが出来ます。
DFTを計算する時、各サンプリング点は、円周上の点の座標を求める様な計算をしています。
言葉ではイメージしにくいと思うので図にしてみます。

2のべき乗の場合(データ数8点)

2のべき乗でない場合(データ数7点)

8点のデータでは、規則性があることがわかります。
例えば、[1,3,5,7]は符号は変わりますが、XYの絶対値はすべて同じになります。
このような対称性や周期性を活かし、計算量を削減することで「高速」にフーリエ変換を行うことができます。

計算量の違い

実際に計算をした場合、測定点数が増えるほどFFTとDFTでは計算量が大きく変わってきます。
下図は計算量の違いをグラフにしたものになります。

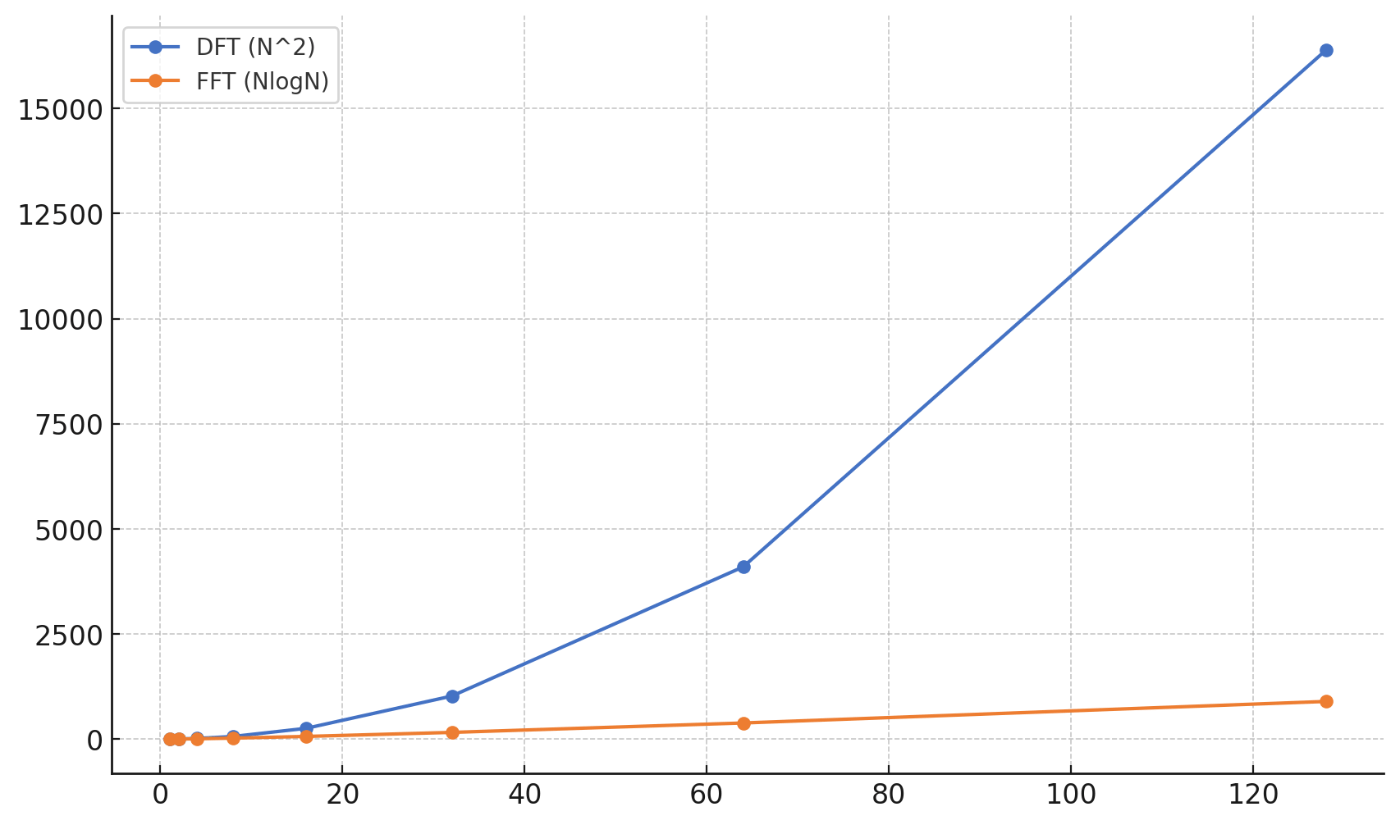
X軸: データ点数（N）
Y軸: 計算に必要な乗算の回数

DFT では、データ点数の二乗の計算回数が必要となるため、少し点数を増やすだけで膨大な計算量となってしまいます。

FFTのアルゴリズムについて

FFTのアルゴリズムにはいくつか種類があります。
代表的なものとしてCooley-Tukey のアルゴリズムがあります。

再帰的な実装

データを偶数番目と奇数番目のデータに分割し、それぞれのサブセットに対して FFTを再帰的に適用します。

反復的な実装

データに対して最小の分割数になるまでバタフライ演算を行った後、データの順番を並び替え FFTを行います。

今後の記事ではReact(TypeScript)とExcelを使ってこのアルゴリズムの説明をしたいと考えています。

DFTの見た目のはなし

グラフで見てみる

下図のような単振動があった場合

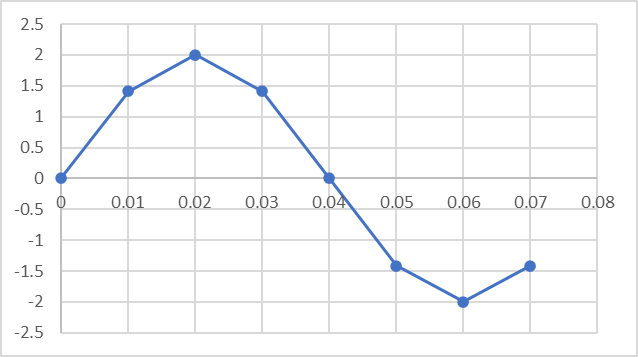
DFTを行うことで各周波数毎に下図のような結果が求められます。

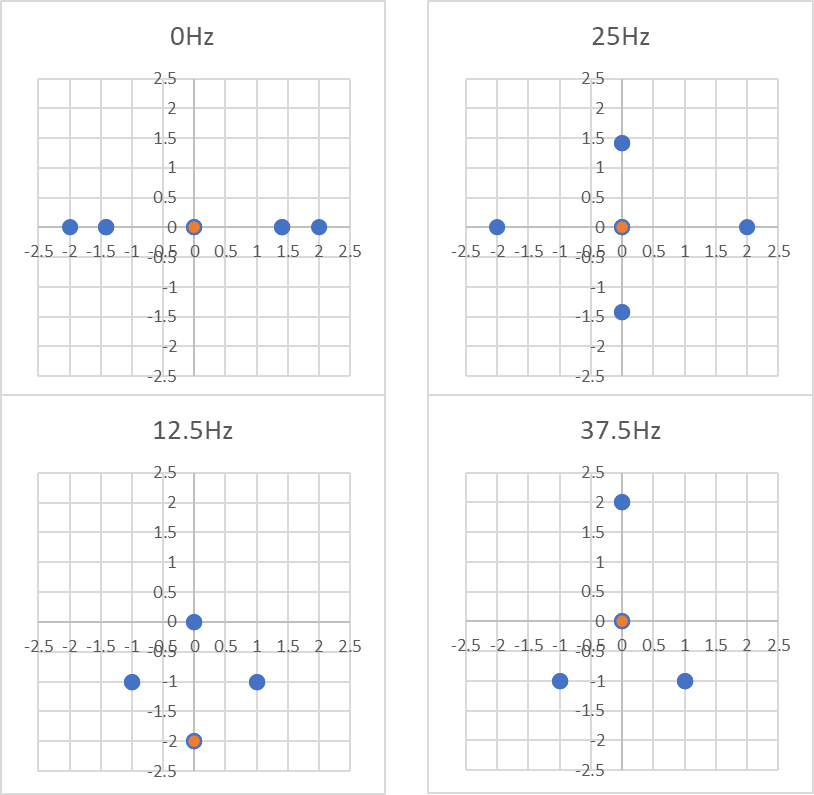
各青点は各サンプル点の複素平面での座標となり、橙点はそれぞれの総和に総サンプル点数で割って2をかけたものになります。

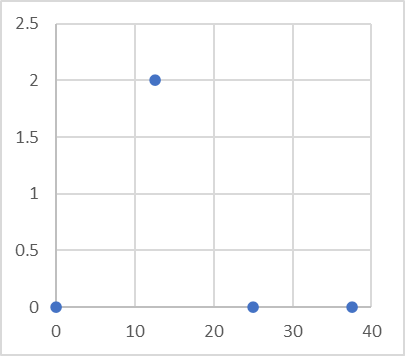
この橙点が0Hzから順にプロットした物が、よく見る周波数軸のグラフになります。

DFTの計算式

DFTの式を見てみたいと思います。

$$X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i2\pi kn/N}$$

ここで、

• $k$:周波数領域インデックス
• $n$:時間領域インデックス
• $X[k]$:周波数軸のk番目の振幅
• $x[n]$:時間軸のn番目の振幅
• $N$:サンプル総点数
• $e^{-i2\pikn/N}$:複素指数関数(周波数領域における各点での信号の位相)
• Σ（シグマ）総和を意味し、n=0からN-1までの和を取ります。

$x[n]$が入力（測定データ等）であり、$X[k]$が出力（変換結果）です。
この式では、入力の各サンプル点$x[n]$が出力$X[k]$の各周波数成分にどのように寄与するかを計算しています。

$k$、$n$はインデックス番号のため、ある測定データがあった時どちらも0から連番をとります。
上記のことから、$X[k]$は、$x[n]$のn番目のデータ夫々に複素指数関数をかけ、総和をとったものということがわかります。

表にした場合(サンプル点が4点の場合)

表にすることで、計算のイメージがつき易くなると思います。
n、kのインデックスに対し、複素指数関数の中でそれぞれマトリックス上にかけた後、総和をとります。

時間	x[n]	インデックス	0	1	2	3	←k
0	$x[0]$	0	$x[0] \cdot e^{-i2\pi 0\cdot0/N}$	$x[0] \cdot e^{-i2\pi 1\cdot0/N}$!	$x[0] \cdot e^{-i2\pi 2\cdot0/N}$	$x[0] \cdot e^{-i2\pi 3\cdot0/N}$
0.01	$x[1]$	1	$x[1] \cdot e^{-i2\pi 0\cdot0/N}$	$x[1] \cdot e^{-i2\pi 1\cdot0/N}$!	$x[1] \cdot e^{-i2\pi 2\cdot0/N}$	$x[1] \cdot e^{-i2\pi 3\cdot0/N}$
0.02	$x[2]$	2	$x[2] \cdot e^{-i2\pi 0\cdot0/N}$	$x[2] \cdot e^{-i2\pi 1\cdot0/N}$!	$x[2] \cdot e^{-i2\pi 2\cdot0/N}$	$x[2] \cdot e^{-i2\pi 3\cdot0/N}$
0.03	$x[3]$	3	$x[3] \cdot e^{-i2\pi 0\cdot0/N}$	$x[3] \cdot e^{-i2\pi 1\cdot0/N}$!	$x[3] \cdot e^{-i2\pi 2\cdot0/N}$	$x[3] \cdot e^{-i2\pi 3\cdot0/N}$
		↑n
		$X[k]$	$X[0]$	$X[1]$	$X[2]$	$X[3]$

まとめ

最後に少し計算式に触れましたが、次回の記事で実際にこの計算をしてみたいと思います。

あとがき

私自身理系の出身ではないので、フーリエ変換という言葉を最初に聞いたのは社会人になってからでした。ある程度自分の中に落としておきたい気持ちもあり、記事を書いています。
説明がおかしいところがあれば教えてもらえると助かります。
javascriptを使って実装するならどうせなら、触れるようなアプリにしたら面白いかなぁとか考えたりもしてます?

おわりに

機械設計やCAD、電子工作についてゆるくつぶやいています。
興味がある方は、ぜひX(旧Twitter)をフォローしてください。