Zenn
〰️

「FFT(高速フーリエ変換)を完全に理解した」になるまで 2(DFT編)

2023/12/23に公開
dft
FFT
tech
まえおき

前回の記事の続きになります。
概要を知りたい方はまずはこちらをよんでください。

DFTを計算してみる。

前回からのおさらいになりますが、まずは DFTの計算を見ていきたいと思います。

数式の確認

X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i2\pi kn/N}
  • k:周波数領域インデックス
  • n:時間領域インデックス
  • X[k]:周波数軸のk番目の振幅
  • x[n]:時間軸のn番目の振幅
  • N:サンプル総点数
  • e^{-i2\pikn/N}:複素指数関数(周波数領域における各点での信号の位相)
  • Σ（シグマ）総和を意味し、n=0からN-1までの和を取ります。

上式を計算する場合、x[0]~x[N-1]にそれぞれe^{-i2\pikn/N}をかけた後、すべてを足すことで、X[0]~X[N-1]が得られることがわかります。

2\piは1回転を表し、kn/Nは、時間領域と周波数領域のインデックス番号をそれぞれかけて総点数で割っています。表にしてみるとイメージがわかりやすいです。

回転成分(2\pikn/N)を表にしてみる(データ数8点の場合)

マトリックスで表現すると下表になります。

  • kを列、nを行のインデックスとしkn/Nを表にすると

    インデックス番号 0 1 2 3 4 5 6 7
    0 \frac{0\times0}{N} \frac{0\times1}{N} \frac{0\times2}{N} \frac{0\times3}{N} \frac{0\times4}{N} \frac{0\times5}{N} \frac{0\times6}{N} \frac{0\times7}{N}
    1 \frac{1\times0}{N} \frac{1\times1}{N} \frac{1\times2}{N} \frac{1\times3}{N} \frac{1\times4}{N} \frac{1\times5}{N} \frac{1\times6}{N} \frac{1\times7}{N}
    2 \frac{2\times0}{N} \frac{2\times1}{N} \frac{2\times2}{N} \frac{2\times3}{N} \frac{2\times4}{N} \frac{2\times5}{N} \frac{2\times6}{N} \frac{2\times7}{N}
    3 \frac{3\times0}{N} \frac{3\times1}{N} \frac{3\times2}{N} \frac{3\times3}{N} \frac{3\times4}{N} \frac{3\times5}{N} \frac{3\times6}{N} \frac{3\times7}{N}
    4 \frac{4\times0}{N} \frac{4\times1}{N} \frac{4\times2}{N} \frac{4\times3}{N} \frac{4\times4}{N} \frac{4\times5}{N} \frac{4\times6}{N} \frac{4\times7}{N}
    5 \frac{5\times0}{N} \frac{5\times1}{N} \frac{5\times2}{N} \frac{5\times3}{N} \frac{5\times4}{N} \frac{5\times5}{N} \frac{5\times6}{N} \frac{5\times7}{N}
    6 \frac{6\times0}{N} \frac{6\times1}{N} \frac{6\times2}{N} \frac{6\times3}{N} \frac{6\times4}{N} \frac{6\times5}{N} \frac{6\times6}{N} \frac{6\times7}{N}
    7 \frac{7\times0}{N} \frac{7\times1}{N} \frac{7\times2}{N} \frac{7\times3}{N} \frac{7\times4}{N} \frac{7\times5}{N} \frac{7\times6}{N} \frac{7\times7}{N}

  • となり、これに2\pi(rad)=360(deg)をかけると

    インデックス番号 0 1 2 3 4 5 6 7
    0 0 0 0 0 0 0 0 0
    1 0 45 90 135 180 225 270 315
    2 0 90 180 270 360 450 540 630
    3 0 135 270 405 540 675 810 945
    4 0 180 360 540 720 900 1080 1260
    5 0 225 450 675 900 1125 1350 1575
    6 0 270 540 810 1080 1350 1620 1890
    7 0 315 630 945 1260 1575 1890 2205

    ※rad単位より、deg(度)の方が説明しやすいので表はdegにしています。
    となります。

回転成分をグラフにしてみる

  • 上記の表だと回転成分がわかりにくいので、0~360degに直してみる。
    インデックス番号 0 1 2 3 4 5 6 7
    0 0 0 0 0 0 0 0 0
    1 0 45 90 135 180 225 270 315
    2 0 90 180 270 0 90 180 270
    3 0 135 270 45 180 315 90 225
    4 0 180 0 180 0 180 0 180
    5 0 225 90 315 180 45 270 135
    6 0 270 180 90 0 270 180 90
    7 0 315 270 225 180 135 90 45
  • グラフにすると下記のようなイメージ

サンプルを作ってExcelで計算してみる

※Excel2021を使って計算しています。
　SEQUENCE関数等の配列関数に対応していない場合、適宜数式を修正する必要があります。

ゴールイメージ

データ数8点の単振動波形を作成して、DFTで周波数軸の波形をに変換するまでを解説していきます。

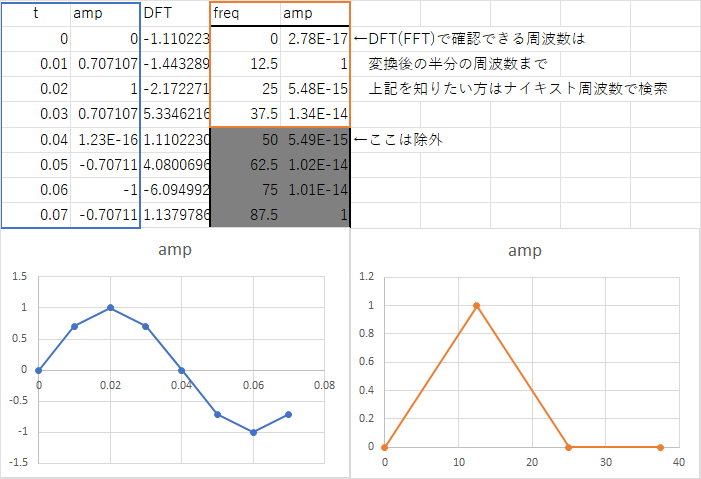
計算の説明

  • 計算結果を先に知りたい方は下記をA1セルに張り付けてください。
  • 解説するためにあえて細かく分けて数式を書いています。
Excelコピペ用(A1セルに張り付け)
DFT.csv
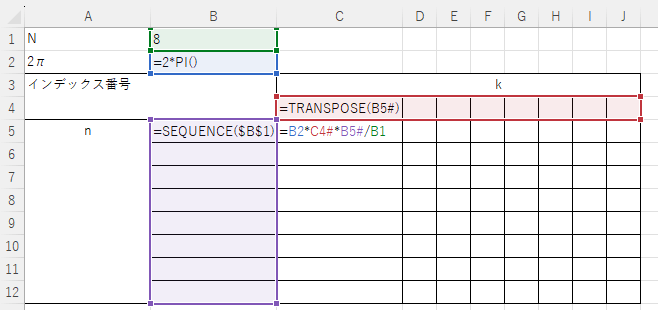
N	8
2π	=2*PI()
インデックス番号					k
		=TRANSPOSE(B5#)
n	=SEQUENCE($B$1)-1	=B2*C4#*B5#/B1








インデックス番号					k
		=TRANSPOSE(B16#)
n	=SEQUENCE($B$1)-1	=COMPLEX(0,-C5#,"i")








インデックス番号					k
		=TRANSPOSE(B27#)
n	=SEQUENCE($B$1)-1	=IMEXP(C16)	=IMEXP(D16)	=IMEXP(E16)	=IMEXP(F16)	=IMEXP(G16)	=IMEXP(H16)	=IMEXP(I16)	=IMEXP(J16)
		=IMEXP(C17)	=IMEXP(D17)	=IMEXP(E17)	=IMEXP(F17)	=IMEXP(G17)	=IMEXP(H17)	=IMEXP(I17)	=IMEXP(J17)
		=IMEXP(C18)	=IMEXP(D18)	=IMEXP(E18)	=IMEXP(F18)	=IMEXP(G18)	=IMEXP(H18)	=IMEXP(I18)	=IMEXP(J18)
		=IMEXP(C19)	=IMEXP(D19)	=IMEXP(E19)	=IMEXP(F19)	=IMEXP(G19)	=IMEXP(H19)	=IMEXP(I19)	=IMEXP(J19)
		=IMEXP(C20)	=IMEXP(D20)	=IMEXP(E20)	=IMEXP(F20)	=IMEXP(G20)	=IMEXP(H20)	=IMEXP(I20)	=IMEXP(J20)
		=IMEXP(C21)	=IMEXP(D21)	=IMEXP(E21)	=IMEXP(F21)	=IMEXP(G21)	=IMEXP(H21)	=IMEXP(I21)	=IMEXP(J21)
		=IMEXP(C22)	=IMEXP(D22)	=IMEXP(E22)	=IMEXP(F22)	=IMEXP(G22)	=IMEXP(H22)	=IMEXP(I22)	=IMEXP(J22)
		=IMEXP(C23)	=IMEXP(D23)	=IMEXP(E23)	=IMEXP(F23)	=IMEXP(G23)	=IMEXP(H23)	=IMEXP(I23)	=IMEXP(J23)

インデックス番号					k
		=TRANSPOSE(B38#)
n	=SEQUENCE($B$1)-1	=IMPRODUCT($B48,C27)	=IMPRODUCT($B48,D27)	=IMPRODUCT($B48,E27)	=IMPRODUCT($B48,F27)	=IMPRODUCT($B48,G27)	=IMPRODUCT($B48,H27)	=IMPRODUCT($B48,I27)	=IMPRODUCT($B48,J27)
		=IMPRODUCT($B49,C28)	=IMPRODUCT($B49,D28)	=IMPRODUCT($B49,E28)	=IMPRODUCT($B49,F28)	=IMPRODUCT($B49,G28)	=IMPRODUCT($B49,H28)	=IMPRODUCT($B49,I28)	=IMPRODUCT($B49,J28)
		=IMPRODUCT($B50,C29)	=IMPRODUCT($B50,D29)	=IMPRODUCT($B50,E29)	=IMPRODUCT($B50,F29)	=IMPRODUCT($B50,G29)	=IMPRODUCT($B50,H29)	=IMPRODUCT($B50,I29)	=IMPRODUCT($B50,J29)
		=IMPRODUCT($B51,C30)	=IMPRODUCT($B51,D30)	=IMPRODUCT($B51,E30)	=IMPRODUCT($B51,F30)	=IMPRODUCT($B51,G30)	=IMPRODUCT($B51,H30)	=IMPRODUCT($B51,I30)	=IMPRODUCT($B51,J30)
		=IMPRODUCT($B52,C31)	=IMPRODUCT($B52,D31)	=IMPRODUCT($B52,E31)	=IMPRODUCT($B52,F31)	=IMPRODUCT($B52,G31)	=IMPRODUCT($B52,H31)	=IMPRODUCT($B52,I31)	=IMPRODUCT($B52,J31)
		=IMPRODUCT($B53,C32)	=IMPRODUCT($B53,D32)	=IMPRODUCT($B53,E32)	=IMPRODUCT($B53,F32)	=IMPRODUCT($B53,G32)	=IMPRODUCT($B53,H32)	=IMPRODUCT($B53,I32)	=IMPRODUCT($B53,J32)
		=IMPRODUCT($B54,C33)	=IMPRODUCT($B54,D33)	=IMPRODUCT($B54,E33)	=IMPRODUCT($B54,F33)	=IMPRODUCT($B54,G33)	=IMPRODUCT($B54,H33)	=IMPRODUCT($B54,I33)	=IMPRODUCT($B54,J33)
		=IMPRODUCT($B55,C34)	=IMPRODUCT($B55,D34)	=IMPRODUCT($B55,E34)	=IMPRODUCT($B55,F34)	=IMPRODUCT($B55,G34)	=IMPRODUCT($B55,H34)	=IMPRODUCT($B55,I34)	=IMPRODUCT($B55,J34)
		=IMSUM(C38,C39,C40,C41,C42,C43,C44,C45)	=IMSUM(D38,D39,D40,D41,D42,D43,D44,D45)	=IMSUM(E38,E39,E40,E41,E42,E43,E44,E45)	=IMSUM(F38,F39,F40,F41,F42,F43,F44,F45)	=IMSUM(G38,G39,G40,G41,G42,G43,G44,G45)	=IMSUM(H38,H39,H40,H41,H42,H43,H44,H45)	=IMSUM(I38,I39,I40,I41,I42,I43,I44,I45)	=IMSUM(J38,J39,J40,J41,J42,J43,J44,J45)
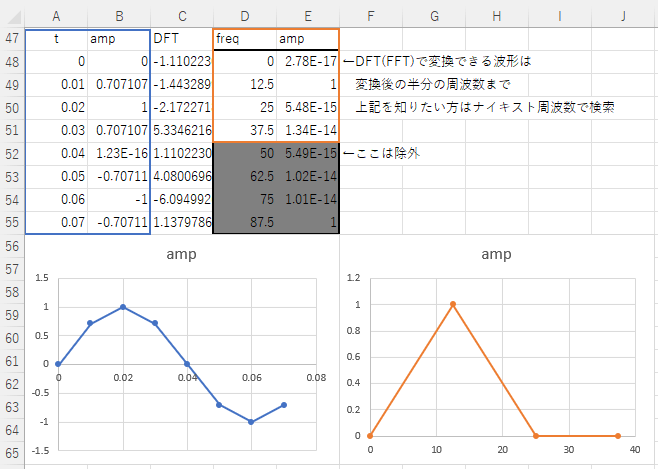
t	amp	DFT	freq	amp
=(SEQUENCE(B1)-1)/100	=SIN((PI()*2/B1*(SEQUENCE(B1)-1)))	=TRANSPOSE(C46:J46)	=1/$A$49/(B1)*(SEQUENCE(B1)-1)	=IMABS(C48)/$B$1*2	←DFT(FFT)で変換できる波形は
				=IMABS(C49)/$B$1*2	　変換後の半分の周波数まで
				=IMABS(C50)/$B$1*2	　上記を知りたい方はナイキスト周波数で検索
				=IMABS(C51)/$B$1*2
				=IMABS(C52)/$B$1*2	←ここは除外
				=IMABS(C53)/$B$1*2
				=IMABS(C54)/$B$1*2
				=IMABS(C55)/$B$1*2

回転因子部分の計算

  • 数式

    1. A1セルにデータ数である8を入力
    2. B1セルに=2*PI()で2\piの計算
    3. B5セルに=SEQUENCE($B$1)-1でnの配列を作成
    4. C4セルに=TRANSPOSE(B5#)でkの配列を作成
    5. C5セルに=B2*C4#*B5#/B1で2\piにn*kの配列をかけて、サンプル点数Nで割る
      ※配列関数がサポートされているExcelでは#を付けることで配列計算できる。

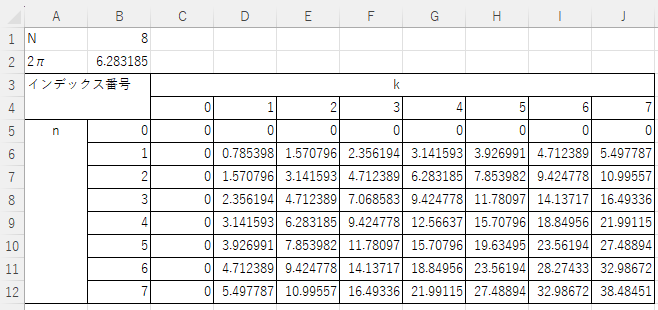
  • 計算結果

複素指数関数の計算

  • 数式

    1. C16セルに=COMPLEX(0,-C5#,"i")で回転因子部分の計算結果に虚数単位をかけ、複素数を作成
    2. C27セル以下に=IMEXP(C16)のように各セルにIMEXP関数を使って複素指数関数を計算
      ※私の使用してているバージョンでは、複素数関数が配列に対応していないため、これ以降は、配列関数ではなく、各セルに直接入力します。

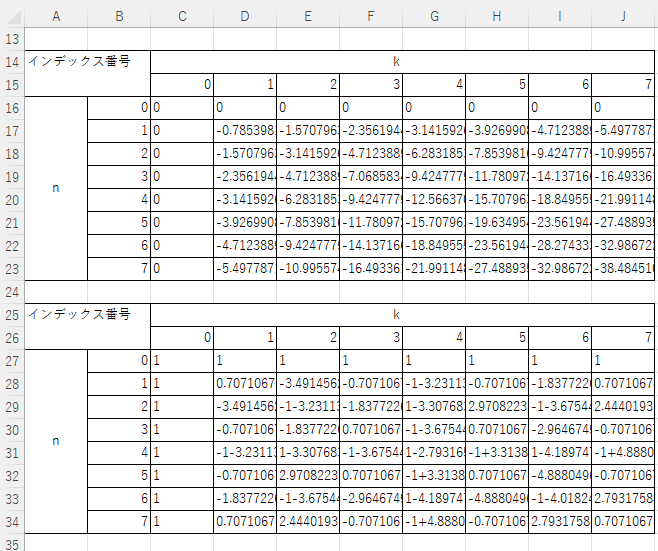
  • 計算結果

    回転因子の各値が複素指数関数によって複素平面上の点として表現されます。

n=0~N-1までの総和の計算

  • 数式

    1. C38セル以下に=IMPRODUCT($B48,C27)のようにIMPRODUCT関数を使い、各行の複素数の積を計算
    2. C46セル以下に=IMSUM(C38,C39,C40,C41,C42,C43,C44,C45)のようにIMSUM関数を使って、各行の複素数の総和を計算
      これにより、各周波数成分の振幅が求められます。

  • 計算結果
    IMSUM関数により計算された各列の総和が、DFTの結果として得られます。
    これは各周波数成分の振幅を表します。

サンプル波形の作成とDFT結果から周波数軸グラフ作成の方法

  • 数式

    1. サンプル波形を作成
      • A48セルに=(SEQUENCE(B1)-1)/100で時間軸の配列を作成
      • B48セルに=SIN((PI())*(2/B1)*((SEQUENCE(B1)-1)))でサイン波の振幅の配列を作成
    2. C48セルに=TRANSPOSE(C46:J46)でDFTの結果配列を置換
    3. D48セルに=1/$A$49/(B1)*(SEQUENCE(B1)-1)で時間軸に対応した周波数軸の配列を作成
    4. E48セル以下に=IMABS(C48)/$B$1*2でDFTの結果から振幅を抽出

  • 計算結果
    サンプル波形とそのDFT結果の周波数軸グラフが表示され、DFTの効果が明確に理解できます。

まとめ

DFTの計算を分解することで、より理解しやすくなると思います。
波形データにDFTを適用することで、その周波数成分を明確に見ることができ、DFTがどのように役立つかがわかります。
※逆に言うと元の時間軸波形以上の情報はとれないので、時間軸波形で充分判断できる場合は周波数軸に変えて確認する必要はないと思います。
次回の記事では、FFTの実装などを解説してみたいと思います。

あとがき

FFTとDFTを説明するにあたり、どの程度まで書くとよいか正直書いた今でも迷っています。
あまり、数学よりになり過ぎたくはない(詳しい解説は他の方が多数説明して頂けてますし)、
でも、この記事を読んでいただけた方に感覚的に理解できて誤った使い方をしなくなる、更に実装もできるくらいになるといいなと思います。

おわりに

機械設計やCAD、電子工作についてゆるくつぶやいています。
興味がある方は、ぜひX(旧 Twitter)をフォローしてください。

GitHubで編集を提案

Discussion