ARIMAを復習するのであります!(時系列解析)
AR(1) 過程と期待値・分散・自己共分散
設定
ただし、
統計量(結果)
以下、定常状態を仮定する。
期待値
分散
自己共分散
自己相関係数
統計量(導出)
期待値
分散
したがって、
自己共分散
自己相関係数
AR(1) 過程の予測値
結果
予測期待値
ただし、
予測分散
導出
予測期待値
予測分散
図で見てわかる AR(1) の予測値の挙動
前回求めたAR(1)過程の予測期待値・予測分散が何を意味しているかを視覚的に理解するために、Pythonでシミュレーションを行なってみた。
以下では、
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(0, 51, 1)
y0 = -1.0
c = 1.2
phi = 0.8
sigma = 1.0
fig, ax = plt.subplots(1,1)
for i in range(0,10):
list_ar1 = []
y_prev = y0
list_ar1.append(y0)
eps = np.random.normal(0, sigma, 50)
for i in range(0,50):
yt = c + phi * y_prev + eps[i]
list_ar1.append(yt)
y_prev = yt
ax.plot(t, list_ar1)
mu = c / (1 - phi)
muk = mu + phi ** t * (y0 - mu)
vk = sigma**2 * (1 - phi ** (2 * t)) / (1 - phi**2)
upper_bound = muk + 1.96 * np.sqrt(vk)
lower_bound = muk - 1.96 * np.sqrt(vk)
ax.plot(t, muk, ls="-", c="gray")
ax.plot(upper_bound, ls="--", c="gray")
ax.plot(lower_bound, ls="--", c="gray")
ax.set_ylabel("$y_t$")
ax.set_xlabel("$t$")

色のついた実線は、異なる乱数を用いて描いた10本のシミュレーション軌道である。
灰色の実線は予測期待値
である(ただし、
灰色の点線は、予測分散
に基づいて計算した95%信頼区間である。
予測分散は
それに合わせて、信頼区間も時間と共に幅が広がりながら最終的には一定の長さに落ち着くことが見てとれる。
シミュレーション軌道は、予測期待値を中心に、おおよそこの点線の範囲内で変動している。
AR(1) 過程のパラメータ推定
設定
以下のようなモデルを考える:
ただし、
パラメータ推定値(結果)
ここで、
とした。
なお、いずれも、不偏推定量ではない。
パラメータ推定方法
係数 c, \phi
最小二乗法による推定を行う。
残差平方和を以下のように定義する:
これを最小化するような
そのためには、残差平方和を偏微分して値が0になる
これを解くと、
のように求まる。
誤差項分散 \sigma^2
いったん天下りに以下のように定義する:
この時、この推定量は
補足: 最尤推定による方法
以下、誤差項が正規分布であると仮定を置く:
このとき、
係数 c, \phi
したがって、
対数尤度は、
この対数尤度関数が最大になる
を最小化する
したがって、先ほどと同様に、
が得られる。
誤差項分散 \sigma^2
そのためには、式(1) を
すると、以下のように求まる:
AR(1) 過程において係数の最小二乗法による推定値が不偏推定量にならないことの説明
以下の記事でAR(1) 過程のパラメータ
ここでは、この時の係数
が不偏推定量にならないことを示す:
(時系列でない)単回帰ではなぜ最小二乗推定が不偏だったか?
まずシンプルな単回帰に立ち戻り、単回帰ではなぜ最小二乗推定による結果が不偏推定量になったのかを復習する。
モデルは、
ただし、
また、
ただし、
このとき
のようになり、
AR(1) モデルの場合
AR(1) モデルでも、
しかし、前述の単回帰の時と異なり、上式の右辺第二項の期待値が0にならない:
なぜかというと、
実際、
と表したとき、
のように
以上から、
まとめ
以上から、AR(1) モデルでは、観測値
補足: y_{t+k} \varepsilon_t
共分散を求めてみると、
AR(1)過程でパラメータ推定量が一致推定量であることを示す
上記の投稿で述べたように、AR(1)過程
(ただし、
のもと、
ただし、
とした。
今回は、これらがパラメータ
回帰係数推定量 \hat{\phi}
上記投稿でも述べたとおり、
このとき、
が成り立つので、
となる。
定数項推定量 \hat{c}
上述のように
であるが、ここで
であるので、
が成り立つ。
なお、
を用いた。
誤差項分散推定量 s^2
AR(1)モデルの定義より
が成立する。
なお、
とした。
ここで、
が成り立つことから、
となる。
従って、移項して両辺を
が得られる。
ここで、
に着目すると、
となることが示される。
補足
(1) \frac{1}{T}\sum_{t=1}^T \varepsilon_{t+1} y_t \xrightarrow{p} 0
詳細は下記書籍の §7.2 を参照のこと:
J. D. Hamilton, Time Series Analysis (1994, Princeton Univ. Press)
(4) \sum_{t=1}^T \hat{\varepsilon}_{t+1} = 0 \sum_{t=1}^T \hat{\varepsilon}_{t+1}y_t = 0
直接的な示し方
であることから
が成り立つことを利用した。
一般的な示し方
下記の投稿のように計画行列 (design matrix)
上記の投稿でも記述したように、回帰式
が与えられたとき、最小二乗法による回帰係数推定量
従って、以下の関係が成り立つ:
ここで、
今回の場合、
に対応するので、
が成り立つことから、
が示される。
AR(1)過程におけるパラメータ推定量の漸近分布
上記の投稿で述べたように、AR(1)過程
では、
ただし、
とした。
さらに、下記の投稿ではこれらの推定量が
今回は、推定量
結果
ホワイトノイズ
このとき、推定量
定数項 c \phi
特に、
誤差項分散 \sigma^2
特に、誤差項
導出
以下にならってベクトル・行列表記をとる:
定数項 c \phi
以下の投稿と同様に、
と表すことができる。
従って、
が成り立つ。
ここで、
と置いて、
が成り立つ(詳細は省略)。
従って、
が成り立ち、さらに今回のケースでは
であることから
が成り立つ。
誤差項分散 \sigma^2
下記の誤差項分散推定量の一致性の箇所で議論したように、
であるので、
のように表すことができる。
このうち右辺第一項については、
が成り立つことから
となる(詳細は省略)。
さらに右辺第二項以降については、
かつ
が成り立つので、いずれも
以上から、
が示された。
なお、誤差項
となる。
補足
ベクトル・行列表現を用いた誤差分散推定量s^2
上記では
まず、推定量
ここで、
に着目してさらに式変形をすると、
のようになる。
なお、二行目から三行目の変換の際に、
という関係を用いた。
よって、
となる。
この式の右辺第一項は上述の通り
であり、右辺第二項については
より
となる。
以上から、
statsmodels で AR(1) モデル
以下のように AR(1) モデル
に従う時系列データ
そのうえで、出力された値が理論をもとにどのように計算されるかを見ていく。
なお、今回はデータ長
import numpy as np
import matplotlib.pyplot as plt
y0 = -1.0
c = 1.2
phi = 0.8
sigma = 1.0
nsample = 100
t = np.arange(0, nsample+1, 1)
fig, ax = plt.subplots(1,1)
list_ar1 = []
y_prev = y0
list_ar1.append(y0)
eps = np.random.normal(0, sigma, nsample)
for i in range(0,nsample):
yt = c + phi * y_prev + eps[i]
list_ar1.append(yt)
y_prev = yt
ax.plot(t, list_ar1)
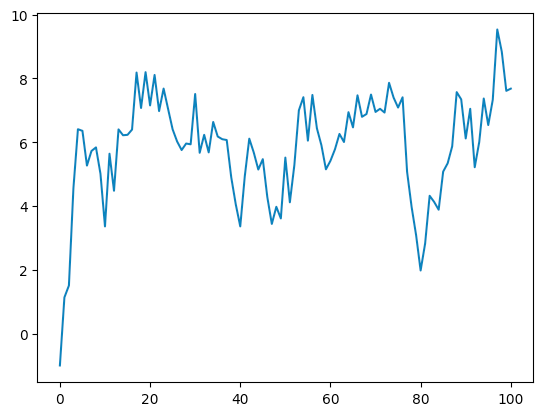
モデル作成
AR モデルの作成には、AutoReg クラスを使用する:
AutoReg では、最小二乗法によりパラメータ
from statsmodels.tsa.ar_model import AutoReg
from statsmodels.graphics.tsaplots import plot_predict
# モデル作成
## AR(p) モデルの次数 p は `lags` で指定
## 今回は定数項 c も含めるため、`trend="c"` のように指定した。
ar_mod = AutoReg(list_ar1, lags=1, trend="c")
ar_res = ar_mod.fit()
# 結果のプロット
fig, ax = plt.subplots()
ax.plot(list_ar1) # 入力データのプロット
plot_predict(ar_res, ax=ax); # 推測値と信頼区間(default では 95%)の表示
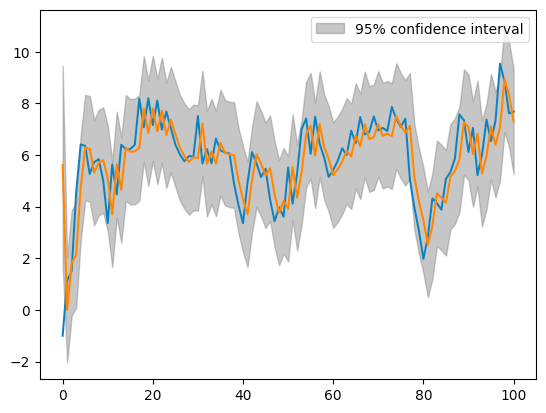
青線は観測値
予測値は、
信頼区間の下限・上限は、誤差項分散推定値
ここで、
予測
観測値を取得した期間より未来の値を out-of-sample 予測することもできる。
以下では、20期先までの予測を行い、その結果を観測値とともにプロットしている。
fig, ax = plt.subplots()
plot_predict(ar_res, start=0, end=120, ax=ax)
ax.vlines(101, *ax.get_ylim(), color="red", linestyles="dashed")
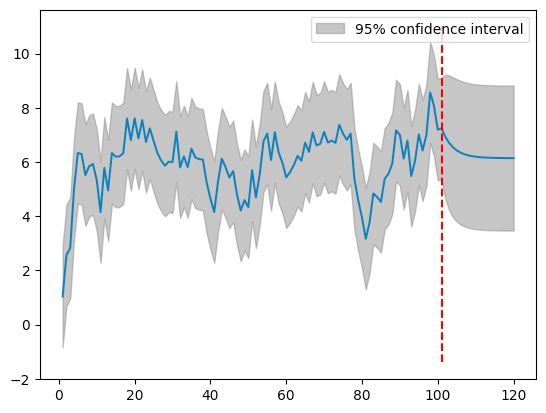
ここでの青線は、区間
ただし、
一方で灰色で表示されているのは95%信頼区間である。
モデル Summary
summary() メソッドを使うことで、モデルに関する統計量を表示できる。
print(ar_res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: y No. Observations: 101
Model: AutoReg(1) Log Likelihood -137.147
Method: Conditional MLE S.D. of innovations 0.954
Date: Tue, 01 Aug 2023 AIC 280.294
Time: 13:35:22 BIC 288.110
Sample: 1 HQIC 283.457
101
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 1.7493 0.348 5.025 0.000 1.067 2.432
y.L1 0.7151 0.057 12.467 0.000 0.603 0.828
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.3983 +0.0000j 1.3983 0.0000
-----------------------------------------------------------------------------
上記で3段に分かれたうちの2段目が、予測パラメータについての統計である。
ここでは、const は定数項 y.L1 は係数
パラメータ推定値
coef 列はパラメータ推定値である。ここでは、
であったことがわかる。
ただし、
なお、誤差項標準偏差 S.D. of innovations に書かれており、
である。
パラメータ標準誤差
std err 列は標準誤差
それぞれ以下のように計算されている:
なぜこうなるかを簡単に示す。下記の投稿より、
が成り立つ。さらに、
が成り立つので、
と見做すと、
となる。
補足: ARIMAクラスとの違い
今回使用した AutoReg クラスのほかに、ARIMA クラスを用いて AR モデルを作成することもできる。
両者の違いは、モデルの推定方法である。
AutoReg は最小二乗法を用いるのに対して、ARIMA はカルマンフィルタを使用する。