Zenn
Open13

Rustで作る自動微分ライブラリの応用ショーケース

Rust
機械学習
自動微分
msakutamsakuta

自動微分ライブラリ rustograd を作ってみた (記事1, 2) りしていますが、考えうる応用があまりにもたくさんあるので、丁寧な解説は抜きにショーケース化したいと思います。

まずは分類問題。機械学習では代表的な問題ですが、これも自動微分の恩恵にあずかれます。

簡単なところから始めて2クラス分類をします。 特徴 x を持つクラス t のサンプルの集まりを (x_i, t_i) (i=0,1,..., N) として訓練データとします。このとき１層ニューラルネットワークで重み行列を W
、 バイアスを \mathbf{b} とすると

\mathbf{s} = W x + \mathbf{b}

というのが第１層の出力になります。

ここでは線形分離可能な単純なケースを考え、１層だけで十分な場合を考えます。すると上記の s はそのままソフトマックス関数へ投入され

y_k = \frac{\exp{s_k}}{\sum_j \exp{s_j}}

となります。ここで f_k はクラス k の予測確率、 s_k は \mathbf{s} ベクトルの第 k 要素です。

これをさらに交差エントロピー誤差関数に通します。

E(W) = -\sum_{n=0}^N \{ t_n \ln y_n + (1 - t_n) \ln(1 - y_n) \}

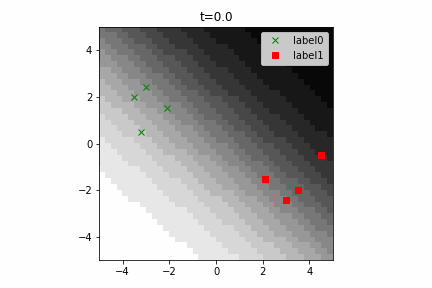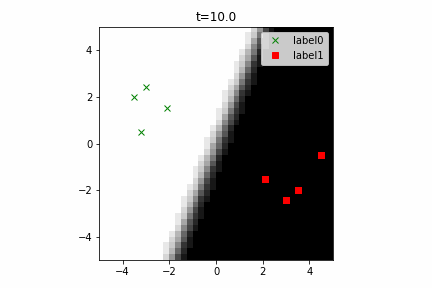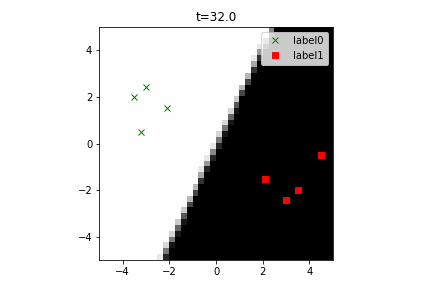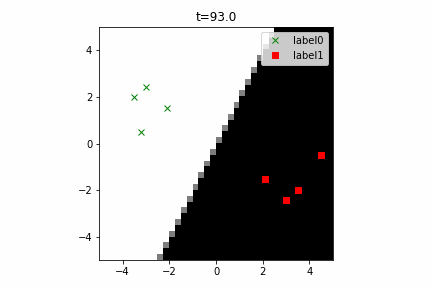
パラメータとなる W (2 x 2 行列) と \mathbf{b} (2 ベクトル) を自動微分によるバックプロパゲーションで学習します。その過程を表したのが次のアニメーションです。白の強度がクラス0への分類確率になります。

このコードは こちら にあります。

msakutamsakuta

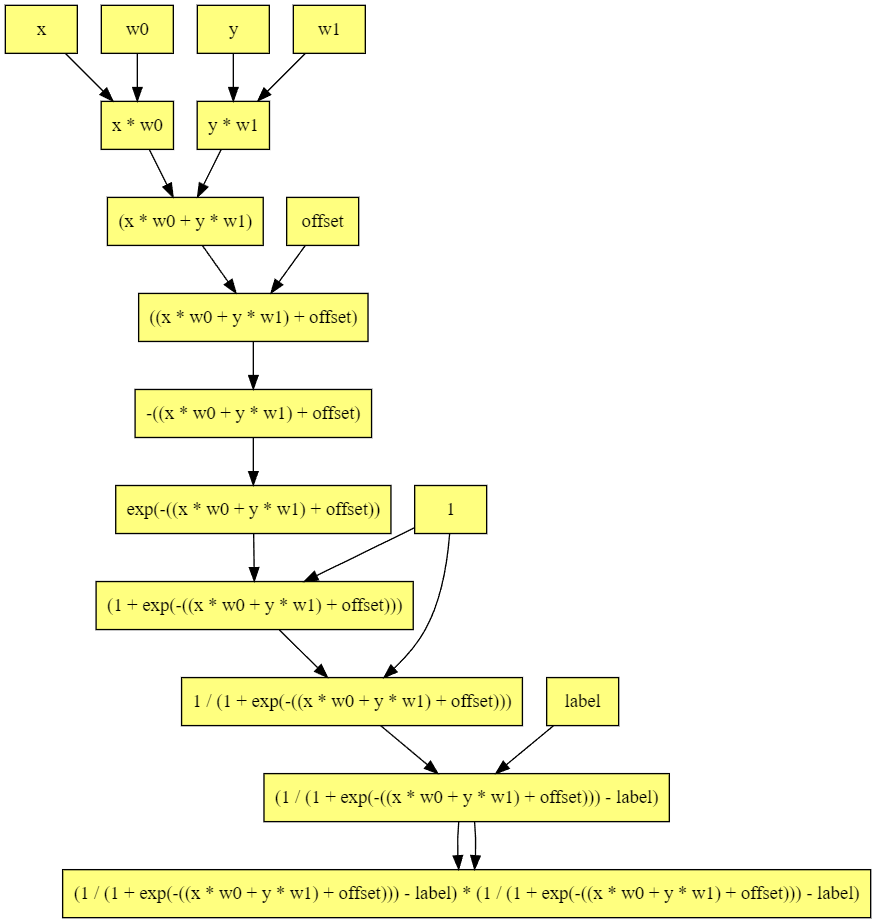
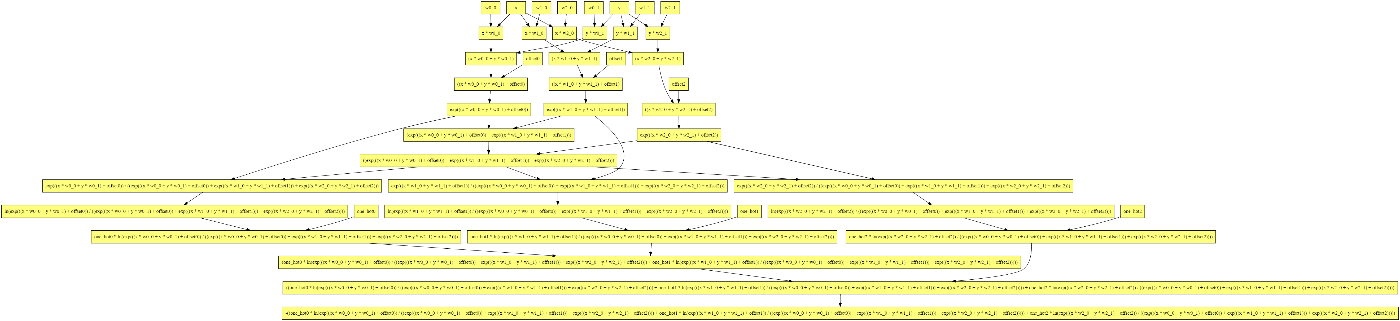
なお、この計算グラフは次のようになります。線形分離可能な２クラス分類という最も簡単な部類の機械学習でもこのぐらい複雑になるんですね。

ただし、計算の効率という意味ではかなり無駄があります。ソフトマックス関数と交差エントロピーの合成をパラメータに関して勾配を取ると、次のようにシンプルな式になるそうです。

\nabla E(W) = \sum_{n=0}^N (y_n -t_n) x_n

自動微分では単純に計算グラフを辿るので、このような式の単純化はできず、愚直にグラフを辿っていくことになります。この影響は速度だけではなく、パラメータの安定性にも関わります。ここではあまり学習回数や勾配降下速度を上げすぎるとパラメータが無限大に発散します。これはソフトマックス関数に指数関数が含まれているからだと考えられます。

詳しくは PRML 4.1.2 節参照のこと。

msakutamsakuta

実は最初にシグモイド関数を直接フィッティングしてロジスティック回帰を試してみたのですが、うまくいきませんでした。シグモイド関数は次のような関数です。

\sigma(x) = \frac{1}{1 + \exp(-x)}

誤差関数は直接クラスの値との差の２乗としていました。

L = \sum_n (\sigma(x_n) - t_n)^2

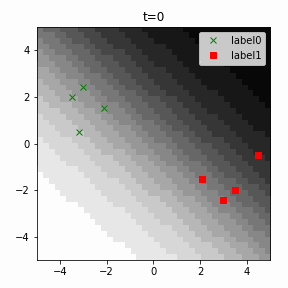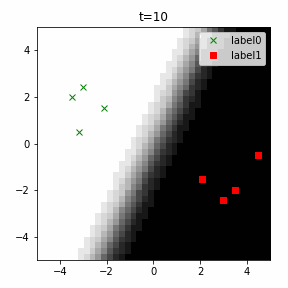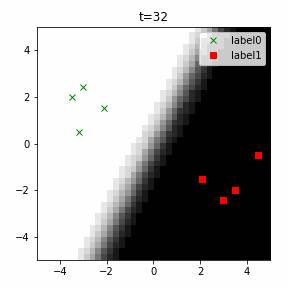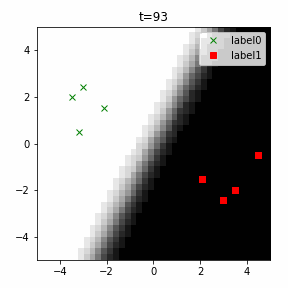
どう上手くいかなかったかは次のアニメーションで明らかだと思います。

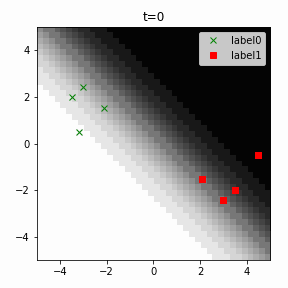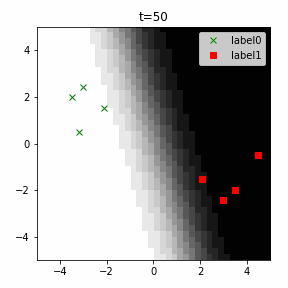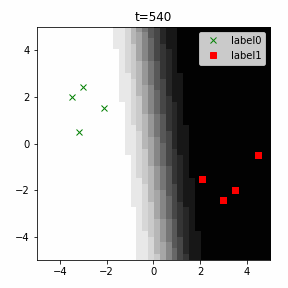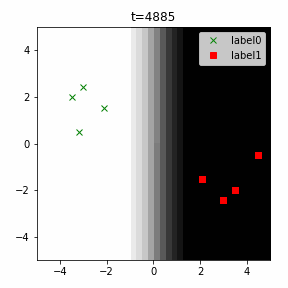
クラス分類こそできているのですが、収束が極めて遅く、ソフトマックス関数と交差エントロピー誤差を使ったときには100回程度の繰り返し計算回数で奇麗に分離できていたのに対し、5000回繰り返してもなんだか真ん中でスパッと分離してくれません(時刻 t は対数スケールにしてあるので、時間経過とともに再生速度が加速していくのに注意してください)。

これはシグモイド関数とクラスの誤差を単純な値の差で評価すると次のようになり、決定境界から離れたサンプルの勾配が非常に小さくなるからだと考えられます。

計算グラフは次のように非常に単純になるのですが、収束が遅い分の影響のほうが大きいです。

「クラス分類問題では二乗誤差よりも交差エントロピー誤差のほうが、収束が早くなると同時に汎化能力が高まることを見い出した。」(PRML p235)という結果があるそうですが、なぜそうなるのかよく理解していないです。

msakutamsakuta

ソフトマックス関数と交差エントロピー誤差はうまく機能してくれるのですが、分離境界があまりにもはっきりしすぎ、白黒はっきりさせないと気が済まないようです。もうちょっと手心というか、サンプルが少ない辺りではグレーゾーンを設けてもいいんじゃないでしょうか。

こんなときは、正則化という手法が有効です。これは誤差関数にパラメータの二乗を加えて、パラメータが極端に大きくなってしまうのを防ぐ方法です。パラメータ \lambda は正則化パラメータと呼ばれ、正則化の強さを制御します。

E(W) = -\sum_{n=0}^N \{t_n \ln y_n + (1 - t_n) \ln(1 - y_n) \} - \lambda || W || ^2

\lambda=1 でグレーゾーンがある程度の幅を維持するようになりました。

計算グラフ上では赤線で囲った部分が正則化で付け加わった部分になります。

正則化は見た目だけの問題ではなく、過学習を防ぐための手法の一つとしても重要です。この例では予測確率を1か0に際限なく近づけていく方向の学習が一方的に行われるので、極端な分類器ができてしまいます。決定境界で領域を２分するだけならあまり違いはないですが、他クラス問題や線形分離できない複雑な問題になってきたときに汎化能力を維持するために重要です。

それは置いておくとして、このような式の調整をしても微分の計算をいちいちし直さなくても自動的に勾配を下ってくれるのはとっても便利ですね。やはり自動微分はすばらしいです。

msakutamsakuta

ここまで来れば他クラス分類もあと一歩です。必要なのは交差エントロピー誤差の定義を一般化して次のようにするだけです。

E(W_1, ..., W_K) = -\sum_{k=1}^K t_k \ln y_k

ここで K はクラスの数、 t は one-hot encode されたラベルです。

以下に3クラスの場合のアニメーションを示します。

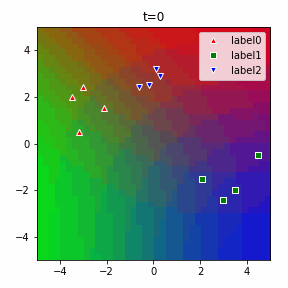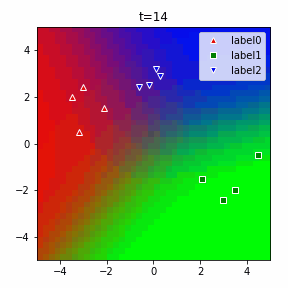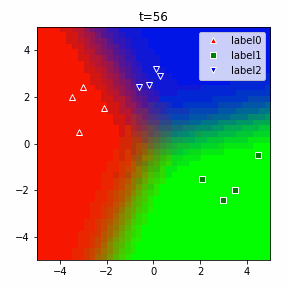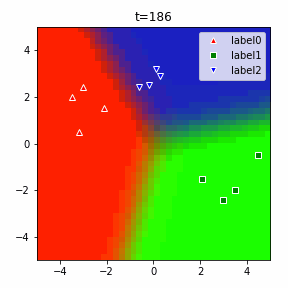
ソフトマックスだの交差エントロピーだのといった込み入った準備は、２クラスでは煩わしいですが、このように他クラス分類に一般化する際にも自然に拡張することができるというメリットがあります。

ソースコードはこちらです。

msakutamsakuta

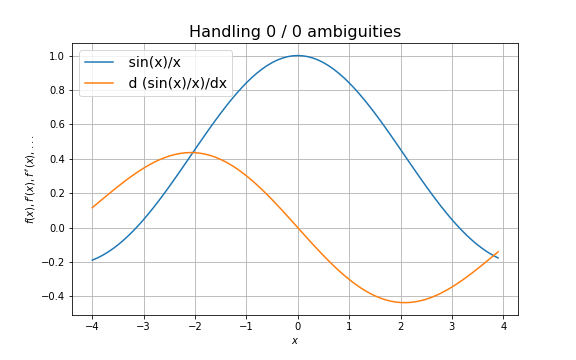
自動微分は 0 / 0 などの値が不定な関数の評価にも使えることがあります。代表的な例は次のようなものです。

f(x) = \frac{\sin(x)}{x}

この関数は x \rightarrow 0 の極限で 1 の値を取りますが、単純に値を代入するだけでは不定になってしまいます。こんなときは l'Hospital の定理で微分係数の比にすると計算できる場合があります。

\lim_{x \rightarrow 0} \frac{f(x)}{g(x)} = \lim_{x \rightarrow 0} \frac{f'(x)}{g'(x)}

これは値の評価と微分係数の評価を同時に行う二重数のような実装では不定な割り算が出てきたときに自動的に適用することができますが、 Tape や計算グラフを作る方法では難しいです。

msakutamsakuta

ロケットサイエンス

自動微分はロケットの軌道計算にも使われているそうです。ここではそれを再現するために超単純化した問題を示します。コードはこちらです。

まずはロケットの状態を位置 \vec{p} と速度 \vec{v} で示します。加速度は \vec{a} で表し、単純に地球(か何らかの重力原となる天体)の位置 \vec{p}_e との差を万有引力係数をモデル化した G でスケールしたものです。本来は Runge-Kutta 法を使って解くべきですが、 rustograd の実装はまだ最適化が十分でなく、あまり大規模な計算グラフを扱えないので、ベレの方法を使います。

\begin{align*} \vec{a} &= G \frac{(\vec{p}_e - \vec{p})}{||\vec{p}_e - \vec{p}||^2} \\ \vec{v} &\leftarrow \vec{v} + \vec{a} \\ \vec{p} &\leftarrow \vec{p} + \vec{v} + \frac{1}{2} \vec{a} \end{align*}

これを数回ループすることで将来の位置を予測します。

計算グラフはループの中身の全ての中間変数を含むので、大きくなります。コード上は下記のようになりますが、最終的に生成されるノードの数は8回のループで 153 個になります。

    let mut accels = vec![];
    let mut vs = vec![vx];
    let mut xs = vec![pos];
    for _ in 0..8 {
        let diff = earth - pos;
        let len = diff.x * diff.x + diff.y * diff.y;
        let accel = diff / len * gm;
        accels.push(accel);
        pos = pos + vx + accel * half;
        xs.push(pos);
        vx = vx + accel;
        vs.push(vx);
    }

    let target_x = tape.term("target_x", 0.);
    let target_y = tape.term("target_y", 1.);
    let last_pos = xs.last().unwrap();
    let diffx = last_pos.x - target_x;
    let diffy = last_pos.y - target_y;
    let loss = diffx * diffx + diffy * diffy;

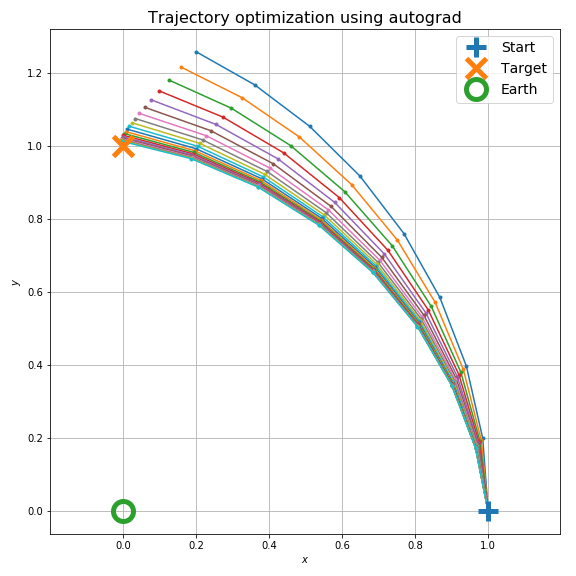
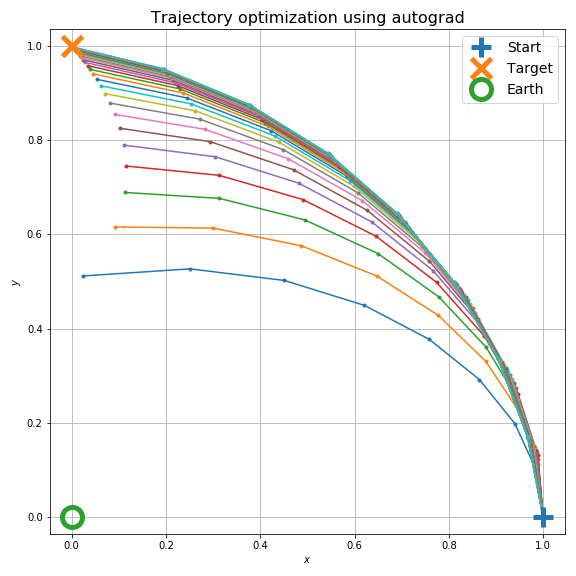
さて、目的はこの軌道を望みの位置に持ってくるように初速を調整することです。ここでは望みの位置 (0, 1) と最終的な位置 \vec{p} の差を損失関数とし、初速 \vec{v} の x, y 成分に関する損失関数の微分を使って最適化してみます。

20回の最適化ループで以下のように軌道が調整できます。

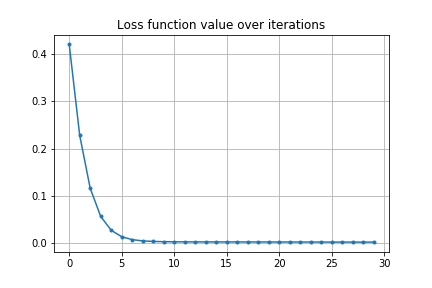
損失関数の変化は以下のグラフのようになります。

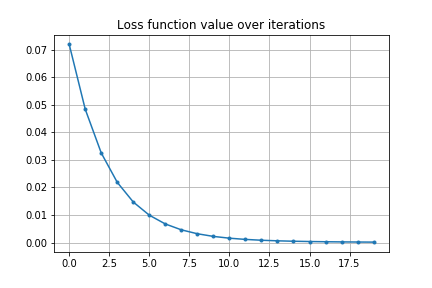
安定性の評価

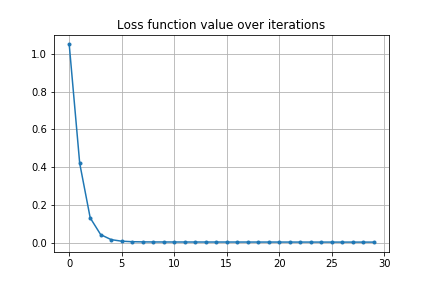
これだけでは初期値の変動に対する安定性があるかよくわかりません。前の例では初期値は目的地をオーバーシュートするような軌道でしたので、今度は初速を下げてアンダーシュートするような軌道から最適化を始めてみます。

結果は以下のようになります。

ここで示したのは非常に単純なモデルで、楕円軌道ならもっと直接的な解法があると思いますが、一般に n-body problem になったときには解析的に解けないので、数値的に軌道計算するしかありません。このような場合でも微分が計算できるのが自動微分の利点です。

msakutamsakuta

前回の計算が間違っていたので仕切り直します ^^;
加速度は長さの正規化の分を含めていませんでした。
また2次の Runge-Kutta 法を使うようにしました。ここで h は時間ステップですがこのシミュレーションでは 1 としています。

\begin{align*} \vec{a}(\vec{p}) &= G \frac{(\vec{p}_e - \vec{p})}{||\vec{p}_e - \vec{p}||^3} \\ \Delta \vec{v}_1 &= h \vec{a}(\vec{p}) \\ \Delta \vec{p}_1 &= h \vec{v} \\ \Delta \vec{v}_2 &= h \vec{a}(\vec{p} + \Delta \vec{p}_1 / 2) \\ \Delta \vec{p}_2 &= h (v + \Delta \vec{v}_1 / 2) \\ \vec{v} &\leftarrow \vec{v} + \Delta \vec{v}_2 \\ \vec{p} &\leftarrow \vec{p} + \Delta \vec{p}_2 \end{align*}

また、もう少し軌道計算っぽく目的地を地球の反対側にしました。
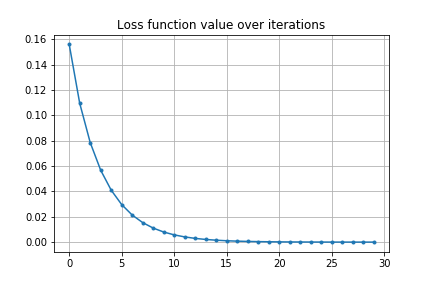
これで最適化過程は次のようになります。

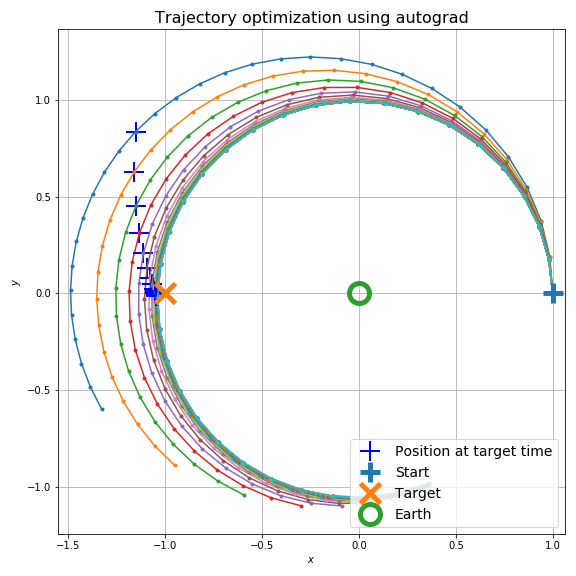
初期値がアンダーシュートする条件では次のようになります。

msakutamsakuta

ちなみにこのときの計算グラフはこんな感じです。それぞれのタイムステップが前のステップに依存するため、依存性の連鎖が非常に長くなります。このレベルになると記号微分は非現実的です。

msakutamsakuta

空気抵抗のある砲弾の軌道最適化

ソース

ロケットの軌道計算と似ていますが、こちらは砲弾の速度による抵抗がある場合のモデルです。

\begin{align*} \vec{a} &= -G\hat{y} - D\frac{\vec{v}}{||\vec{v}||^2} \\ \vec{v} &\leftarrow \vec{v} + \vec{a} \\ \vec{p} &\leftarrow \vec{p} + \vec{v} + \frac{1}{2} \vec{a} \end{align*}

ここで G は重力加速度、 D は空気抵抗による速度の減衰率、タイムステップは 1 としています。

空気抵抗がなければ放物線になり、解析的に容易に解けますが、空気抵抗は非線形な微分方程式となり、解析的に解くのは簡単ではありません。そこで何も考えずに次のようにモデルを立て、自動微分を適用します。

    let mut pos = Vec2 {
        x: tape.term("x", 0.),
        y: tape.term("y", 0.),
    };
    let mut vx = Vec2 {
        x: tape.term("vx", 0.75),
        y: tape.term("vy", 0.5),
    };

    let gm = tape.term("GM", GM);

    let zero = tape.term("0.0", 0.0);
    let half = tape.term("0.5", 0.5);
    let drag = tape.term("drag", 0.02);
    let mut accels = vec![];
    let mut vs = vec![vx];
    let mut xs = vec![pos];
    for _ in 0..30 {
        let velolen2 = vx.x * vx.x + vx.y * vx.y;
        let velolen12 = velolen2.apply(
            "pow[3/2]",
            |x| x.powf(1. / 2.),
            |x| 1. / 2. * x.powf(-1. / 2.),
        );
        let accel = gravity(zero, gm) - vx * drag / velolen12;
        let delta_x2 = vx + accel * half;
        pos = pos + delta_x2;
        accels.push(accel);
        xs.push(pos);
        vx = vx + accel;
        vs.push(vx);
    }

    let target = Vec2 {
        x: tape.term("target_x", 10.),
        y: tape.term("target_y", 0.),
    };
    let last_pos = *xs.last().unwrap();
    let diff = last_pos - target;
    let loss = diff.x * diff.x + diff.y * diff.y;

最適化計算は下図のようになります。空気抵抗のため砲弾発射直後と着弾時の X 方向の速度が非対称であることが見て取れますが、目標に着弾するように最適化ができていることがわかります。

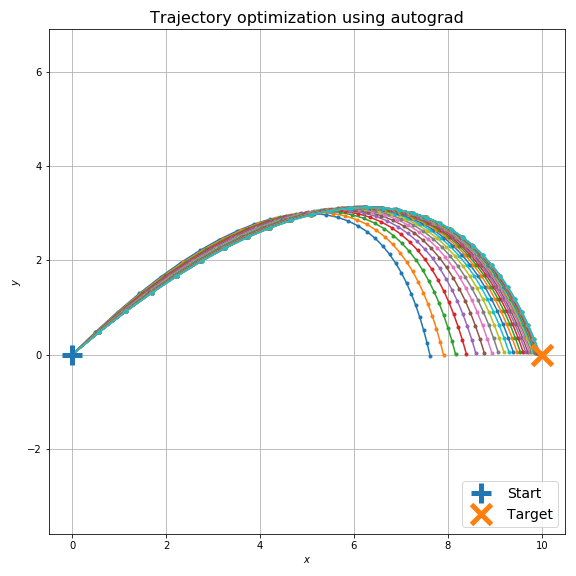
もちろん、初期条件でオーバーシュートする場合も大丈夫です。

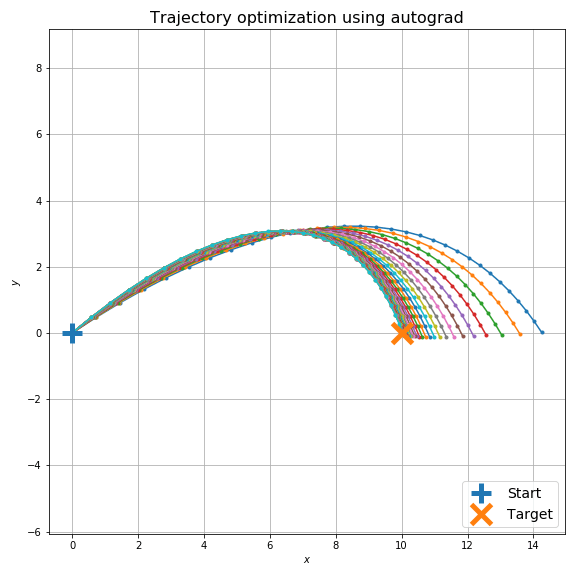
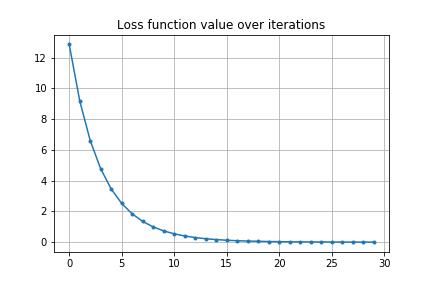
ちょっと極端な例ですが、初期条件で逆方向に砲弾を打ち出していても最適化できます。

msakutamsakuta

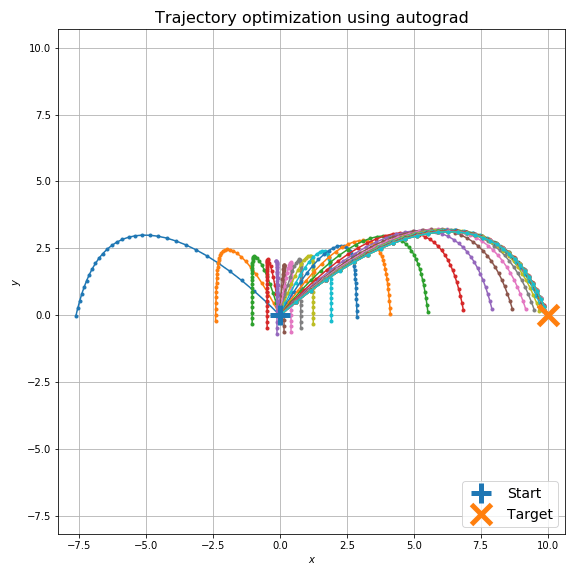
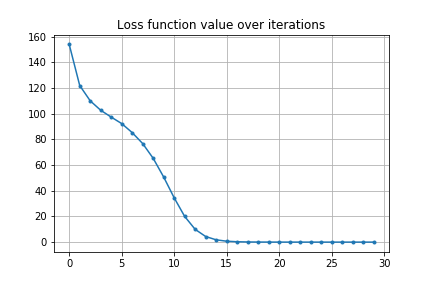
空気抵抗下で2つの砲弾を空中衝突させる

ソース

もっとクレイジーな最適化も考えられます。前の空気抵抗下の砲弾と同じですが、2つの砲弾を空中で衝突させることを考えます。やることは砲弾のシミュレーションを2つに増やすことと、損失関数を固定の目標との距離から2つの砲弾の距離に変えることだけです。

解が対称だとつまらないので、発射点の高さを変えて非対称にしています。

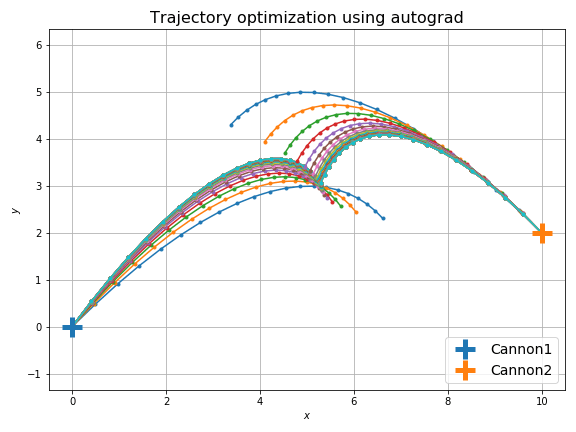
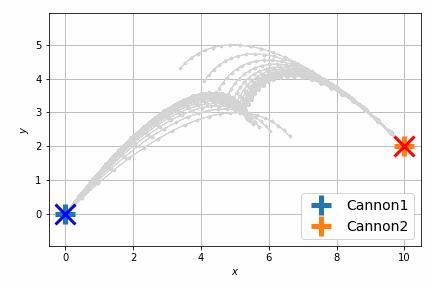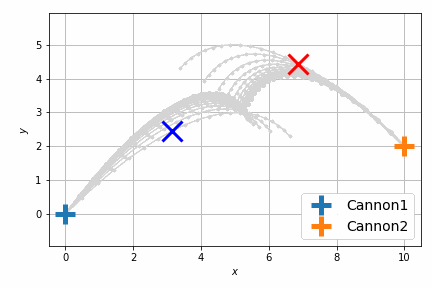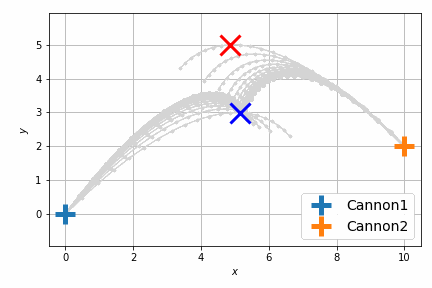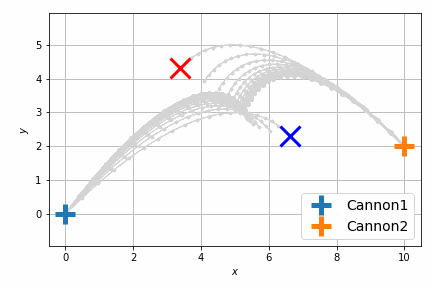
これだけだとよくわからないので、砲弾の軌跡をアニメーションにします。次に示すのは最適化前です。

最適化後はこんな感じです。

msakutamsakuta

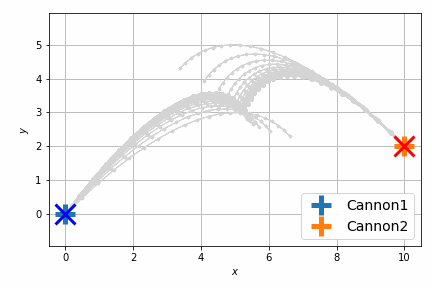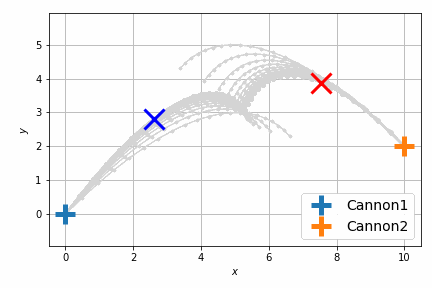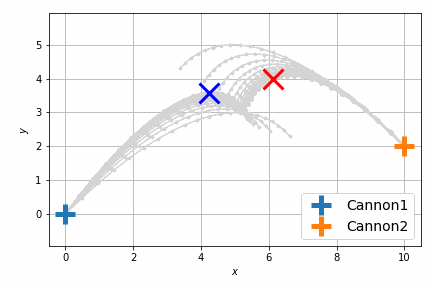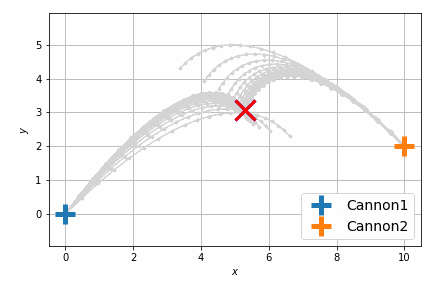
前回は砲弾のシミュレートを固定のステップ数 (20回) 行い、最後のステップで衝突させましたが、衝突させること自体が目的であれば、最後のステップで衝突する必要はなくて、衝突するならばいつでもよいわけです。つまり砲弾のシミュレーションの過程のいずれかの瞬間における距離が最小になればよいのです。

このような条件をモデル化するため、 min 関数を自動微分の計算グラフに導入します。 rustograd には任意の2変数関数を定義する機能が最近追加されましたので、 BinaryFn トレイトを実装することでこれを実現します。

struct MinOp;

impl rustograd::BinaryFn<f64> for MinOp {
    fn name(&self) -> String {
        "min".to_string()
    }

    fn f(&self, lhs: f64, rhs: f64) -> f64 {
        lhs.min(rhs)
    }

    fn t(&self, data: f64) -> (f64, f64) {
        (data, data)
    }

    fn grad(&self, lhs: f64, rhs: f64) -> (f64, f64) {
        if lhs < rhs {
            (1., 0.)
        } else {
            (0., 1.)
        }
    }
}

モデルとしては2項演算子と似ています。左と右のオペランドのうち小さいほうを選ぶという演算は次のように素直に実装されます。

impl rustograd::BinaryFn<f64> for MinOp {
    fn f(&self, lhs: f64, rhs: f64) -> f64 {
        lhs.min(rhs)
    }
}

ちょっとトリッキーなのは微分係数の計算です。2変数関数には入力が2つありますので、微分の結果も2つあることになります。このため grad トレイトメソッドは2つの値を返します。 min 関数の場合、左を選んだら左の微分係数がそのまま使われ、右を選んだら右が使われますので、次のような条件になります。

impl rustograd::BinaryFn<f64> for MinOp {
    fn grad(&self, lhs: f64, rhs: f64) -> (f64, f64) {
        if lhs < rhs {
            (1., 0.)
        } else {
            (0., 1.)
        }
    }
}

これで2つの変数の最小値とその微分係数を自動微分で求めることができますが、最終的に求めたいのは砲弾の軌跡上の全てのタイムステップでの最小値です。とはいえ、2つが合成できるならいくつでもできます。ここでは hist1 と hist2 にそれぞれの砲弾の状態の履歴を記憶しており、その距離の最小値を次のように計算できます。

    let loss = hist1
        .iter()
        .zip(hist2.iter())
        .fold(None, |acc: Option<TapeTerm<'a>>, cur| {
            let diff = cur.1.pos - cur.0.pos;
            let loss = diff.x * diff.x + diff.y * diff.y;
            if let Some(acc) = acc {
                Some(acc.apply_bin(loss, Box::new(MinOp)))
            } else {
                Some(loss)
            }
        })
        .unwrap();

結果は次のようになります。

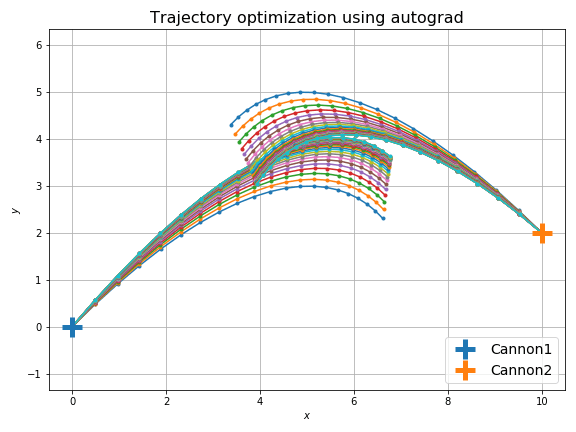
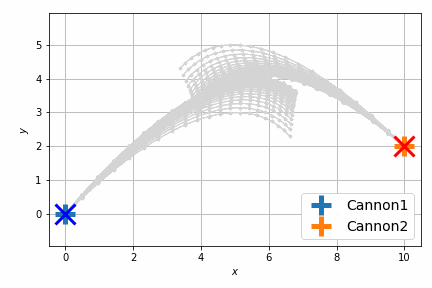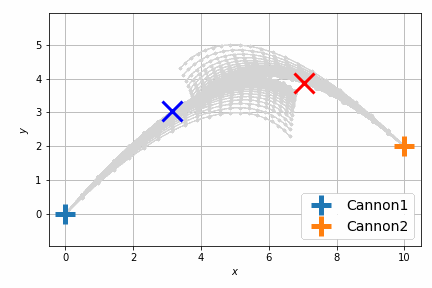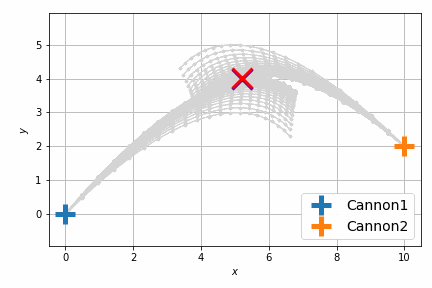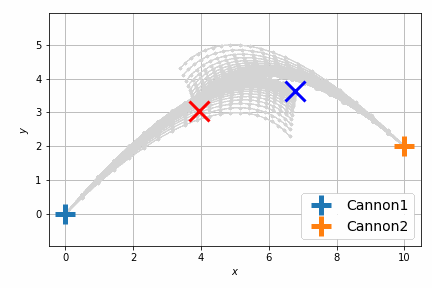
以前よりも自然に最短距離で衝突するようになりました。

msakutamsakuta

モデル予測制御

ソース

さて、砲弾にロケットエンジンをつけて空中で加速をつけられるようにしたらどうなるでしょうか。これは要するにミサイルですね。動的に目標を追跡するような制御ができるようになります。

前回までは発射時点での向きと速度のみを制御していましたが、ミサイルの制御は刻々と変化していく自分と目標の状態に応じる必要があります。このような制御の中でもよく使われているのがモデル予測制御 (Model Predictive Control) です。

モデル予測制御は、要するに物理モデルに基づいて短いシミュレーションを行い、目的の状態(位置・速度・向きなど)からの誤差を最小にするような最適化制御です。非常に多くのバリエーションがありますが、最初に一度だけ最適化計算をするのではなく、時間発展とともに継続的に計算を繰り返すという特徴があります。このためモデルが不正確だったり、外乱が加わったり、計測誤差があったとしてもそれを修正しながらそれなりの解を求めることができます。

能書きはこれくらいにして、実際の制御結果を見てみましょう。

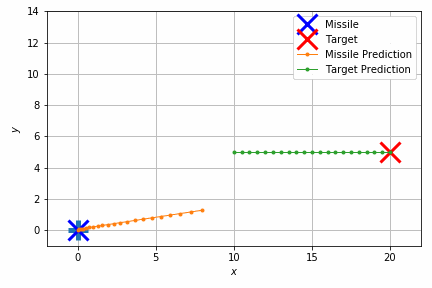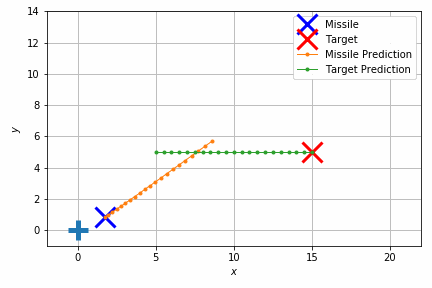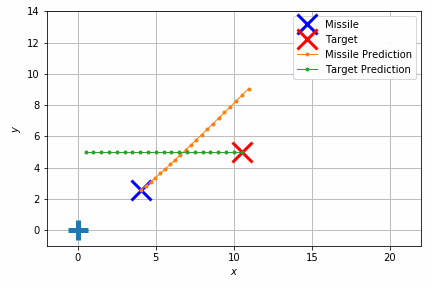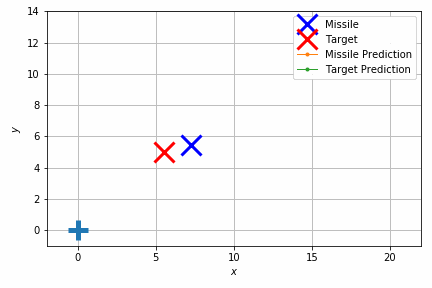
このシミュレーションでは重力のほかにランダムな速度を加えて外乱を再現しています。それでもターゲットの移動体にそれなりの正確さで当たっていることが見て取れます。

結果だけ見ると簡単そうに見えますが、実際には加速度や向きの制約があり、急に向きを変えたりすることはできません。このため将来を見通して加速度や向きを調整する必要があります。

このような制御でよく使われているのは他に PID 制御があり、計算量が非常に少ないという利点がありますが、パラメータ調整が難しくなりがちです。モデル予測制御はモデル上で最適化したい条件を直接指定できるので(この場合はターゲットとミサイルの最小距離)、職人技のようなパラメータ調整をしなくても済み、条件の変動に対して頑健でもあります。