はじめに
【情報数学】にてこの記事の目的について読んで頂けると幸いです。
線形代数のスクラップ
行列式
n次正方行列Aに対して\\
\operatorname{det}A\stackrel{def}{=}\sum_{i_1,i_2,\dots,i_n=1}\epsilon_{i_1i_2\dotsi i_n}a_{i_11}a_{i_22}\cdots a_{i_nn}
\epsilon_{i_1i_2\dotsi i_n}はレヴィ=チヴィタ記号です。
しかしまあ意味不明なので2次正方行列をみていきます。
\begin{aligned}
\operatorname{det}
\left(
\begin{array}{c}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{array}
\right)
&=\sum_{i_1,i_2=1}\epsilon_{i_1i_2}a_{i_11}a_{i_22}\\
&=\epsilon_{11}a_{11}a_{12}+\epsilon_{12}a_{11}a_{22}+\epsilon_{21}a_{21}a_{12}+\epsilon_{22}a_{21}a_{22}\\
&=\epsilon_{12}a_{11}a_{22}+\epsilon_{21}a_{21}a_{12}\\
&=a_{11}a_{22}-a_{21}a_{12}
\end{aligned}
\epsilon_{11}=0,\epsilon_{12}=1,\epsilon_{21}=-1であることに注意しましょう。
幾何学的意味
行列式は符号付きの体積拡大率を表しています。
単純に次のような座標変換を考えると
\begin{pmatrix}
x'\\
y'\\
z'
\end{pmatrix}
=
\begin{pmatrix}
2&0&0\\
0&3&0\\
0&0&4\\
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
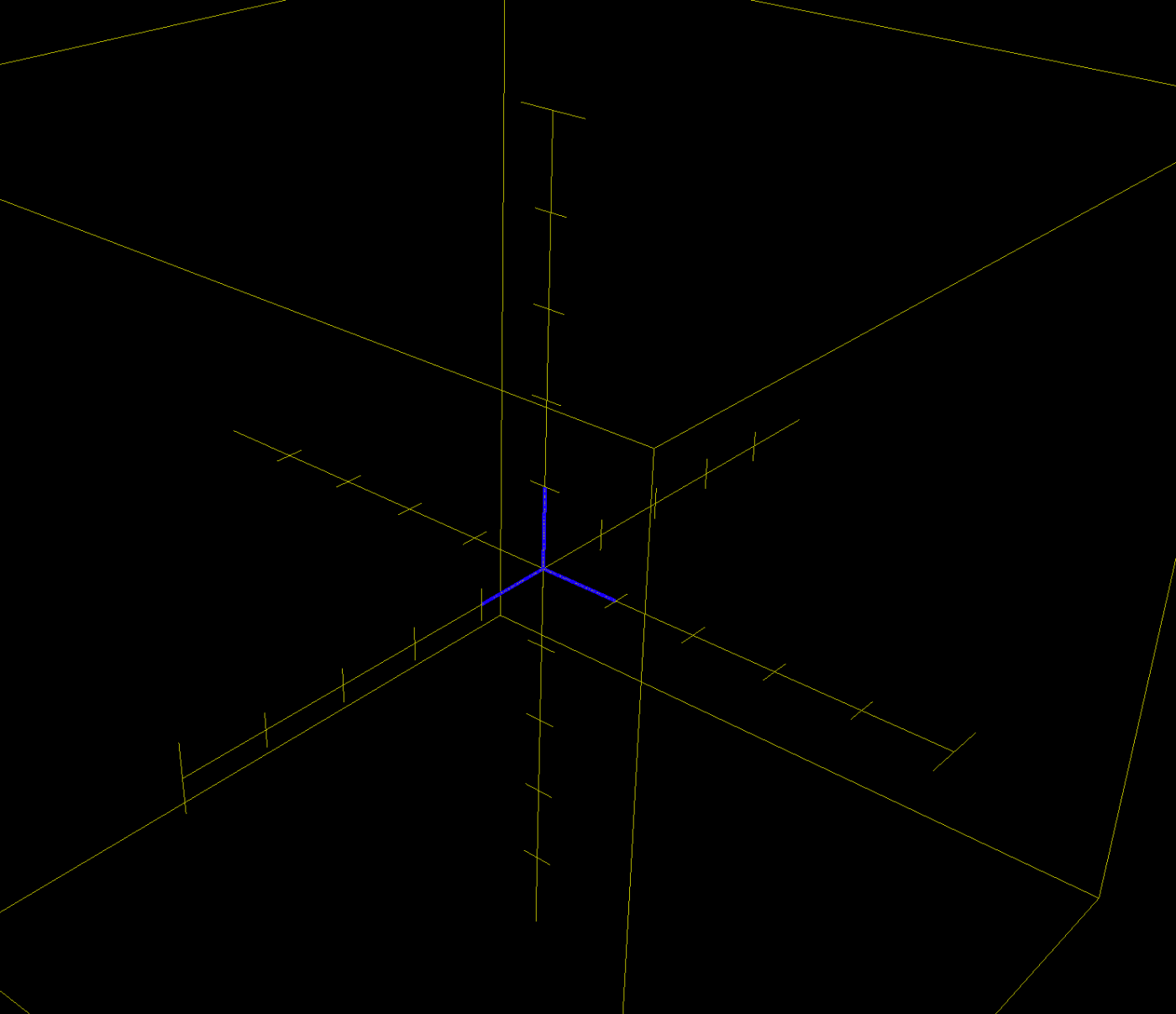
標準基底が
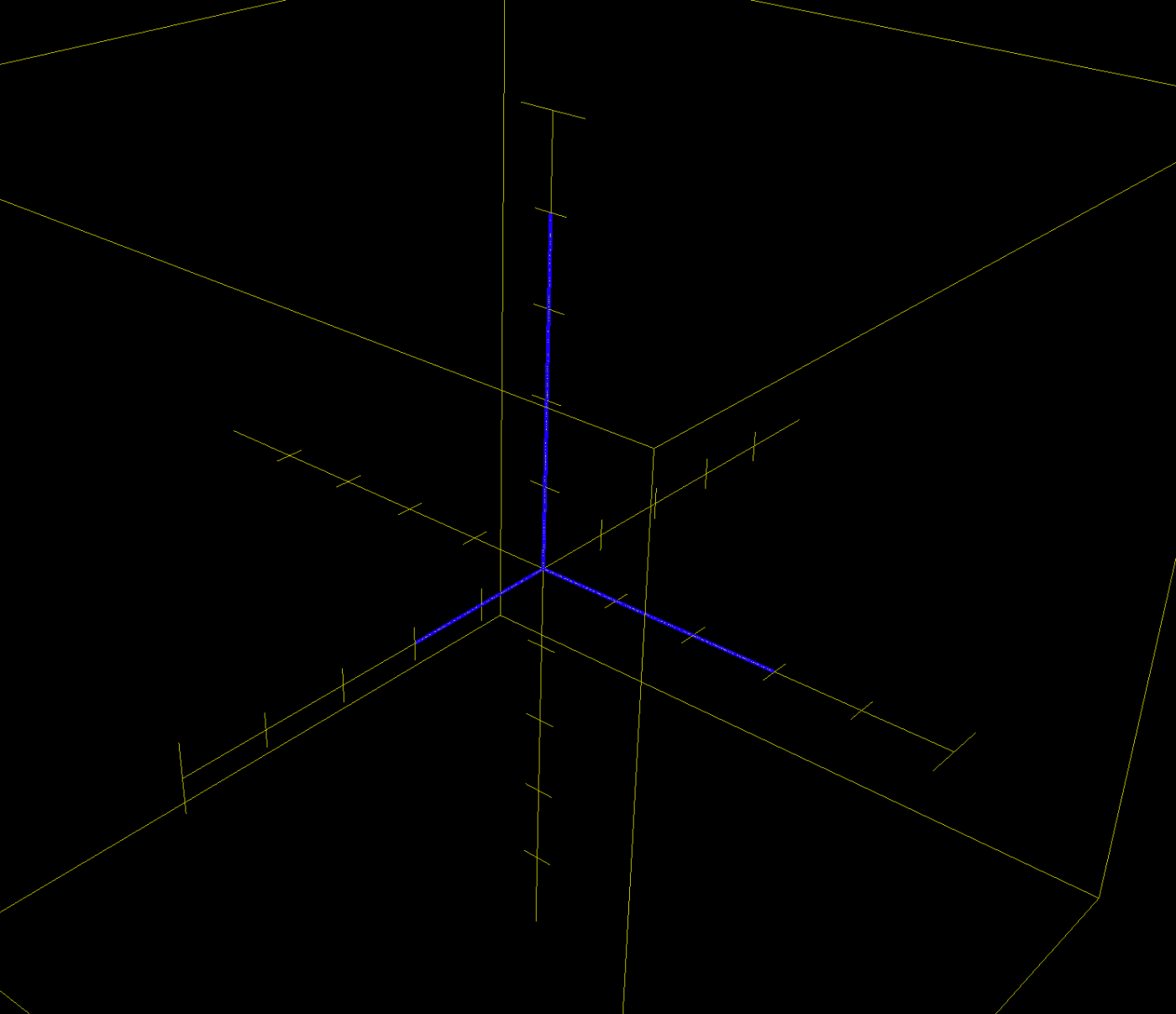
こうなります。
標準規定が張る並行六面体の体積が\det A=2\times3\times4倍になっています。
今回はただ座標を引き伸ばしただけですが、回転するような複雑な変換でも行列式と(符号付きの)体積拡大率は一致します。
(というかMacのGrapherとかいうアプリで図作ってみたけど死ぬほど使いづらくてこれが限界。どうすればいいんだ。)
抽象的な定義
f \colon A \in M(n,n) \rightarrow \mathbb{K} \\
\begin{aligned}
&(1) \quad 多重線形性\\
&(2) \quad 退化性\\
&(3) \quad 正規化条件\\
\end{aligned}\\
の3つを満たすとき、f(A)は行列式である。
証明
標準基底\{\mathbf{e}_1,\mathbf{e}_2, \dots , \mathbf{e}_n\}を用いて各列ベクトルを線形結合で\\
表示すると多重線形性により\\
\begin{aligned}
A
&=(\sum_{i_1}a_{i_11}\mathbf{e}_{i_1},\sum_{i_2}a_{i_21}\mathbf{e}_{i_2}, \dots ,\sum_{i_n}a_{i_n1}\mathbf{e}_{i_n})\\
&=\sum_{i_1,i_2, \dots ,i_n=1}a_{i_11}a_{i_22}\dots a_{i_nn}\operatorname{det}(\mathbf{e}_{i_1},\mathbf{e}_{i_2}, \dots , \mathbf{e}_{i_n})\\
\end{aligned}\\
ここで\operatorname{det}(\mathbf{e}_{i_1},\mathbf{e}_{i_2}, \dots , \mathbf{e}_{i_n})は、添字が\operatorname{det}(\mathbf{e}_{1},\mathbf{e}_{2}, \dots , \mathbf{e}_{n})のとき、\\
正規化条件により1になる。交代性により\mathbf{e}_{i_1},\mathbf{e}_{i_2}, \dots , \mathbf{e}_{i_n}を並び変えて\\
\mathbf{e}_{1},\mathbf{e}_{2}, \dots , \mathbf{e}_{n}にする際、1回置換する事に(-1)倍されるがこの回数\\
は偶置換か奇置換のどちらかが一意的に定まるので\\
\begin{aligned}
&\sum_{i_1,i_2, \dots ,i_n=1}a_{i_11}a_{i_22}\dots a_{i_nn}\operatorname{det}(\mathbf{e}_{i_1},\mathbf{e}_{i_2}, \dots , \mathbf{e}_{i_n})\\
=&\sum_{i_1,i_2, \dots ,i_n=1}\epsilon_{i_1,i_2,\dots,i_n}a_{i_11}a_{i_22}\dots a_{i_nn}\operatorname{det}(\mathbf{e}_{1},\mathbf{e}_{2}, \dots , \mathbf{e}_{n})\\
=&\sum_{i_1,i_2, \dots ,i_n=1}\epsilon_{i_1,i_2,\dots,i_n}a_{i_11}a_{i_22}\dots a_{i_nn}
\end{aligned}\\
多重線形性
線形空間V_1,V_2, \dots ,V_nの各ベクトルとスカラーについて、\\
f( \mathbf{v}_1, \mathbf{v}_2, \dots ,k\mathbf{v}_i+l\mathbf{v'}_i, \dots ,\mathbf{v}_n)\\
=kf( \mathbf{v}_1, \mathbf{v}_2, \dots ,\mathbf{v}_i, \dots ,\mathbf{v}_n)+ lf( \mathbf{v}_1, \mathbf{v}_2, \dots ,\mathbf{v'}_i, \dots ,\mathbf{v}_n)\\
退化性
線形空間V_1,V_2, \dots ,V_nの各ベクトル\mathbf{v}_1, \mathbf{v}_2, \dots ,\mathbf{v}_nについて\\
一つでも同じものがあるとき\\
f( \mathbf{v}_1, \mathbf{v}_2, \dots ,\mathbf{v}_i, \dots ,\mathbf{v}_n)=0
正規化条件
行列式の性質
基本変形
\begin{aligned}
&(1) \quad ある列をスカラー倍したものを他の列に足しても行列式は変わらない。\\
&(2) \quad ある列をk倍すると行列式はk倍になる。\\
&(3) \quad ある列と他の列を入れ替えると(-1)倍になる。\\
\end{aligned}
基本変形に少し条件がついただけです。
これらは前述の抽象的な定義から証明できます。
転置
\operatorname{det}A=\operatorname{det}\!^{t}A
行と列を入れ替えても影響が無いということなので、行基本変形を行っても問題ありません。
積
\operatorname{det}(AB)=(\operatorname{det}A)(\operatorname{det}B)
体積拡大率であることを考えれば当たり前です。
逆行列
\operatorname{det}A^{-1}=\frac{1}{\operatorname{det}A}
第1列が特殊なとき
\operatorname{det}
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & a_{m2} & \cdots & a_{mn}
\end{pmatrix}
=
a_{11}\operatorname{det}
\begin{pmatrix}
a_{22} & \cdots & a_{2n} \\
\vdots & \ddots & \vdots \\
a_{m2} & \cdots & a_{mn}
\end{pmatrix}\\
第1行と第1列が丸々なくなります。
交代性によるサイズ変更
第i行が1である標準基底\mathbf{e}_iを第j列にもつ行列A \in M(n,n)の\\第i行と第j列を除いた行列M_{ij}を用いて\\
\operatorname{det}(\mathbf{a}_1,\mathbf{a}_2,\dots,\mathbf{e}_i,\dots,\mathbf{a}_n)=(-1)^{i+j}\operatorname{det}M_{ij}
証明
\mathbf{e}_iの第i行の成分である1を他の成分の順序を変えないように(1,1)にもっていくことを考える。\\
まず第1行へもっていくためにi-1回入れ替えを行い、そこから第1列へもっていくのにi-1回\\
入れ替えを行えばいいから合計i+j-2回の入れ替えを要する。最後にサイズを変更すれば\\
\operatorname{det}(\mathbf{a}_1,\mathbf{a}_2,\dots,\mathbf{e}_i,\dots,\mathbf{a}_n)=1\times(-1)^{i+j-2}\operatorname{det}M_{ij}=(-1)^{i+j}\operatorname{det}M_{ij}となる。
余因子展開
A \in M(n,n)の第i行と第j列を除いた行列M_{ij}を用いて\\
\Delta _{ij}\stackrel{def}{=}(-1)^{i+j}\operatorname{det}M_{ij}\\
をAの余因子という。
この余因子を用いると行列式を次のように展開できます。
\operatorname{det}A=\sum_{k}a_{ik}\Delta_{ik}=a_{i1}\Delta_{i1}+a_{i2}\Delta_{i2}+\dots+a_{in}\Delta_{in}
証明
標準基底 \{\mathbf{e}_1,\mathbf{e}_2, \dots , \mathbf{e}_n\}を用いて第j列を線形結合で表示すると\\
多重線形性により\\
\begin{aligned}
A
&=(\mathbf{a}_1,\mathbf{a}_2,\dots,\sum_{i}a_{ij}\mathbf{e}_i,\dots,\mathbf{a}_n)\\
&=\sum_{i}a_{ij}\operatorname{det}(\mathbf{a}_1,\mathbf{a}_2,\dots,\mathbf{e}_i,\dots,\mathbf{a}_n)\\
&=\sum_{i}a_{ij}(-1)^{i+j}\operatorname{det}M_{ij}
\end{aligned}
行と列は入れ替えてもいいので列について展開しても大丈夫です。
余因子行列による逆行列の導出
\operatorname{adj}A\stackrel{def}{=}\!^t(\Delta _{ij})\\
を余因子行列という。
余因子を成分に持つ行列です。
これを用いて逆行列は次のようになります
A^{-1}=\frac{1}{\operatorname{det}A}\operatorname{adj}A
証明
\begin{aligned}
(A\operatorname{adj}A)_{ij}
&=\sum_{k}(A)_{ik}(\operatorname{adj}A)_{kj}\\
&=\sum_{l}a_{ik}\Delta_{jk}\\
&=
\begin{cases}
\operatorname{det}A\quad(i=j)\\
0\quad(i\not ={j})\quad (退化性による)
\end{cases}
\end{aligned}\\
ゆえに
A\operatorname{adj}A=diag(\operatorname{det}A,\operatorname{det}A,\dots,\operatorname{det}A)
となるから\\
A(\frac{1}{\operatorname{det}A}\operatorname{adj}A)=\frac{1}{\operatorname{det}A}A\operatorname{adj}A=I_n\\
(\frac{1}{\operatorname{det}A}\operatorname{adj}A)Aについても同様。
つまり、行列式とAの全ての成分に関する余因子を求めれば逆行列を得られます。
計算が大変すぎるので役に立ちませんが...
しかしこの式をよくみると\operatorname{det}A\not ={0}なら逆行列が存在するということになります。これが線形代数3-3の同値表現(6)の説明になります。
行列式が0
行列式が0というのは、幾何学的には体積が0になるということになります。
3次元空間なら縦横高さのうち少なくとも一個がなくなってしまったということです。
言い換えれば、線形独立だった基底が線形従属になってしまう=基底が減るともいえます。
これはよく考えてみれば当然の事態で、行列は基底を変えてしまうわけですからその基底が変換後も基底で居続けられるかは行列の気分次第です。
標準規定の行き先は行列の列ベクトルですから、行列が正則かどうか(=基底が基底で居続けられるかどうか)というのは行列の列ベクトルが線形独立か否かというのがさらなる同値表現として考えられそうです。
これは次回説明します。


Discussion