【因果推論】層化無作為化実験(Stratified RCT)をPythonで実装してみた
無作為化実験(RCT)は、因果推論の基本的な手法として実証分析で多く活用されているのみならず、「A/Bテスト」という名前でビジネスにおける効果検証手法としても活用されていることは周知の事実だと思います。
そんなRCTの一種に、層化無作為化実験(Stratified RCT/層化A/Bテスト) があります。この手法は、共変量の値をもとに個体を層に分け、層ごとにRCTを実施し、各層の推定量を重みづけして全体の平均処置効果の推定量を得る手法です。共変量の偏りを小さくするRCT手法である層化RCTは、2024年話題の川口、澤田(2024)「因果推論の計量経済学」、及び安井、伊藤、金子(2024)「Pythonで学ぶ効果検証入門」でも取り上げられています。
本記事では、前述の「Pythonで学ぶ効果検証入門」で触れられていなかった、層化RCTの不偏推定量の取得過程を、人工疑似データを用いてPythonで実行することを目的としております。
層化RCTの説明は簡単に触れますが、あくまでも本記事の目的は層化RCTの不偏推定量の取得過程に関するPythonコードをご紹介することですので、層化RCTの詳しい説明に関しましては前述のとても分かりやすい書籍をご参照頂きますと幸いです。
本記事内の情報、コードの誤りがありましたら、コメントで教えていただきますと幸いです。
RCTに対する問題意識と、層化RCTの仕組み
RCT実行時に発生しうる問題の一つは、Treatment GroupとControl Groupに属するサンプルに偏りが生じうる、ということです。このGroup間の共変量の不均衡を防ぐために、層化RCTでは共変量に基づいた層化を行い、層ごとに独立したRCTを実行して処置効果を推定し、それらを適切に重み付けして全体の平均処置効果(ATE)を算出します。得られた推定量は、RCTから得られたATEに比べて分散が小さくなり、特に結果と強く相関する共変量に基づいて層化を行うと精度の向上が顕著になるとされています(Athey, Imbens(2017))。
より詳細な説明やメリット・デメリット、具体的なユースケースに関しては、前述の「因果推論の計量経済学」、「Pythonで学ぶ効果検証入門」、およびAthey, Imbens(2017)"The Econometrics of Randomized Experiments"に詳しく書かれておりますので、ご参照ください。
ATEの不偏推定量の算出方法
層化RCTにおいて、ATEを算出する方法を二通り紹介します。これら以外の導出方法や、推定量の不偏性の証明、分散の導出等に関しては、前述の「因果推論の計量経済学」をご参照ください。
その1 ~層ごとの平均の差をとる方法~
個体の共変量に基づき、層を1,2,…,Sに分ける。各層で同一の処置割り当て確率を置き、層sにおける平均処置効果を
-
\overline{Y}_{t,s} -
\overline{Y}_{c,s}
このとき、全体の平均処置効果
-
n_s -
N
この
その2 ~回帰~
Yを層ダミーと、層ダミーと処置ダミーの交差項とに回帰することで得られる交差項の係数が、各層の平均処置効果の推定量、すなわち「その1」の
回帰式は以下の通り
-
S_{is} -
Z_i
上記の回帰式で得られた
層化RCTを実行するPythonコード
実行場面の設定
ECサイト会員に向けて購入プロセスの簡素化施策を実施したことが、実際の購買につながったかどうかの効果検証を行うケースを想定します。このECサイトは、カゴ落ち(購入放棄)に悩んでいると仮定します。そのためサイト運営会社は、購入までのプロセスの一部を簡素化することで、かご落ちを防ぎ購買の完結を促したいと考えています。今回は、この効果を検証するためにA/Bテストを実行する場面を想定します。
結果変数は、ユーザーごとの、購入かごに入れた全アイテムに対する実際に購入されたアイテムの割合とします。
共変量は、ユーザーの年齢と会員歴(年)とします。また、上記の結果変数は、共変量の一部とTreatmentに依存すると考えます。
人工データの作成
人工データ作成および処置割り当てのコード作成においては、うとしん(2023)「Pythonで因果推論(3)~介入とランダム化比較試験~」を参考にさせていただきました。
今回、各層で3割をTreatment Group、7割をControl Groupにすることとします。加えて、処置を行うことの効果を0.4として結果変数を作成します。
import numpy as np
import pandas as pd
def make_covariate(n_samples, seed):
np.random.seed(seed)
#共変量1:年齢を正規分布(平均35歳、標準偏差10歳)から生成
ages_continuous = np.random.normal(35, 10, size=n_samples).astype(int)
ages_continuous = np.clip(ages_continuous, 20, 49) # 年齢範囲を20歳〜49歳に制限
#共変量2:会員歴
membership_years = np.random.randint(1, 10, size=n_samples)
#共変量をデータフレームにまとめる
df = pd.DataFrame({
'age_continuous': ages_continuous,
'membership_years': membership_years
})
#年齢層を10年区切りで作成
df['Age_Group'] = pd.cut(df['age_continuous'], bins=[20, 30, 40, 50], labels=[f'{i}0s' for i in range(2, 5)], right=False)
#年層を3年区切りで作成
df['Year_Group'] = pd.cut(df['membership_years'], bins=np.arange(1, 11, 3), labels=[f'{i}-{i+2}' for i in range(1, 8, 3)], right=False)
#年齢をダミー化
df['20s'] = (df['Age_Group'] == '20s').astype(int)
df['30s'] = (df['Age_Group'] == '30s').astype(int)
#層ごとにグループ番号を振る
df['Group'] = df.groupby(['Age_Group', 'Year_Group']).ngroup()
#各グループごとにTreatmentを割り当て
ratio = 0.3 #処置割当比率
rng = np.random.default_rng(seed)
df['Treatment'] = 0
for group, group_df in df.groupby('Group'):
num_samples = round(len(group_df) * ratio)
treat_indices = rng.choice(group_df.index, num_samples, replace=False)
df.loc[treat_indices, 'Treatment'] = 1
#ノイズとYスコア(目的変数、購入かごに入れた全アイテムに対する実際に購入されたアイテムの割合)の生成
df['Y_noise'] = np.random.normal(0, 0.1, n_samples)
df['Y_score'] = (
0.1 * df['20s'] +
0.1 * df['30s'] +
0.05 * df['membership_years'] +
0.4 * df['Treatment'] +
df['Y_noise']
)
return df
#データセットを作成
df = make_covariate(n_samples=1000, seed=4)
print(df[['Group', 'Age Group', 'Year Group']].value_counts().sort_index(level='Group', ascending=True))
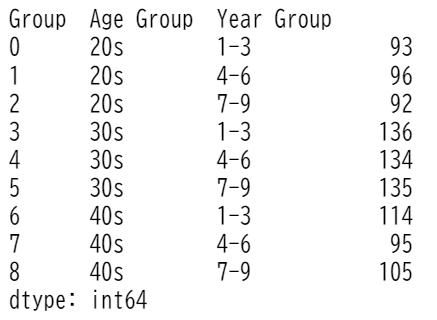
共変量に基づいて層化されたことが確認できます。
【追記(2024.12.02)】「# 年齢範囲を20歳〜49歳に制限」の部分において、50歳以上のユーザーを切り捨てることを意図していましたが、誤って50歳以上のユーザーを丸め込むコードとなってしまいました。今回のテーマからして、推定量の算出には大きな影響がないためこのままといたします。
推定量の取得 ~その1~
処置の平均処置結果は以下の通り。
tau = 0
tau_list = []
for g in range(0, 9):
mean_treatment = df[df['Group'] == g][df['Treatment'] == 1]['Y_score'].mean()
mean_control = df[df['Group'] == g][df['Treatment'] == 0]['Y_score'].mean()
tau_list.append(mean_treatment - mean_control)
tau += ((mean_treatment - mean_control) * len(df[df['Group'] == g])/len(df))
print(tau)

想定通り、平均処置効果は0.4に近い値となりました。
また、各層の平均処置効果は以下の通りです。
print(tau_list)

層ごとに値のばらつきはあるものの、今回はおおむねどの層も平均処置効果が0.4になっています。こうした層ごとの平均処置効果の値の違いを、効果の異質性として捉えることができます。
推定量の取得 ~その2~
各層の平均処置効果は、各層のダミー変数と処置のダミー変数の交差項の係数で表されます。
import statsmodels.formula.api as smf
#回帰分析
model = smf.ols(formula='Y_score ~ C(Group) + C(Group):C(Treatment)', data=df).fit()
print(model.summary())
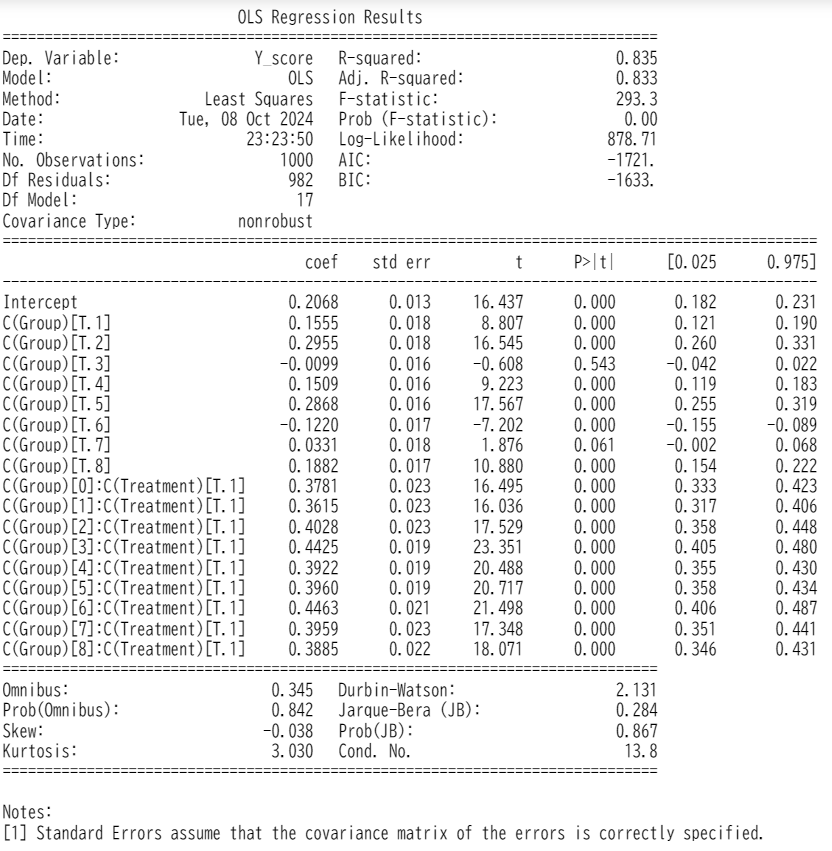
各層のATEは1%有意水準でも有意であるという結果を得ました。
また、全体の平均処置効果は以下の手順で取得されます。
#1.交差項の係数を取得
coefficients = [model.params[f'C(Group)[{i}]:C(Treatment)[T.1]'] for i in range(9)]
#2.Groupごとのサンプル数をカウントして全体比を計算
group_counts = df['Group'].value_counts().sort_index()[:9] # グループ0〜8の人数
group_ratios = group_counts / group_counts.sum() # 全体に対する割合
#3.交差項の係数に人数の割合を重みづけして総和を計算
weighted_sum = np.dot(coefficients, group_ratios)
print(f'重み付けした総和: {weighted_sum}')

この結果から、全体の平均処置効果、および各層の平均処置効果は、その1で取得したものとその2で取得したものが一致することを確認できます。
おわりに
本記事では、層化RCTにおける平均処置効果の推定量の算出方法、および実装のためのPythonコードを紹介しました。層化RCTは推定量の分散を小さくして精度を高めることができるほか、層ごとにRCTを行うため、効果の異質性も観察できるという利点があります。
通常のRCTに比べて層化を行うコストはあるものの、より効果検証の精度を上げる手法としてビジネスでも活用できるのではないかと思います。近年では機械学習手法などを用いて効果の異質性を観察するケースも見られますが、そうした手法にくらべて層化RCTは仕組みが分かりやすく、A/Bテストを理解している方は比較的容易に活用できると思います。
本記事では層化における共変量の選択や変数化に関しては議論していません。とりわけ、共変量を離散化する段階で閾値に分析者の恣意性が入り込む可能性があり、その功罪については筆者は理解できていないので、今後の課題としたいと思います。
Discussion