初めに
これからしばらく準同型暗号の一方式CKKS (Cheon-Kim-Kim-Song)を紹介します。Microsoftが開発しているSEALなどで実装されています。
CKKSの記事一覧
完全準同型暗号の概要
完全準同型暗号FHE(fully homomorphic encryption)とは暗号文を復号することなく、暗号文を操作できる暗号です。数学的には暗号文の加算と乗算を任意回計算できます。実際には演算回数が制限される場合も多く、その場合は厳密にはレベルド(leveled)準同型暗号といいます。
たとえば、生成AIは便利ですが企業で使う場合は情報漏洩が心配です。もしAIサーバのデータ処理にFHEを使えれば、
- 処理したいデータmを暗号化して
- 暗号文c=Enc(m)をサーバに渡し、
- サーバ側で暗号文のままデータを処理して暗号文c'=f(c)を生成し、
- それをクライアントに戻します。
- 最後にクライアントはc'を復号して処理結果Dec(c')=f(m)を得られます。
AIサーバに秘密情報を渡さなくてよいので大変ありがたいです。このようなことが出来るように日々研究が進められています。CKKSはレベルド準同型暗号の一つで、今まで紹介してきた楕円曲線暗号ではなく格子暗号と呼ばれるジャンルです。実数や複素数係数の多項式を使うため、しばらく多項式に関する数学的な準備をしましょう。ハードな内容ですが、丁寧に説明したつもりなので頑張ってください。
1のべき乗根
Mを4以上の2のべき乗の形の整数で、i:=\sqrt{-1}、\xi:=e^{2i\pi/M}とします。\xiは1のM乗根（\xi^M=1）です。
1の8乗根の例（M=8, N=4）
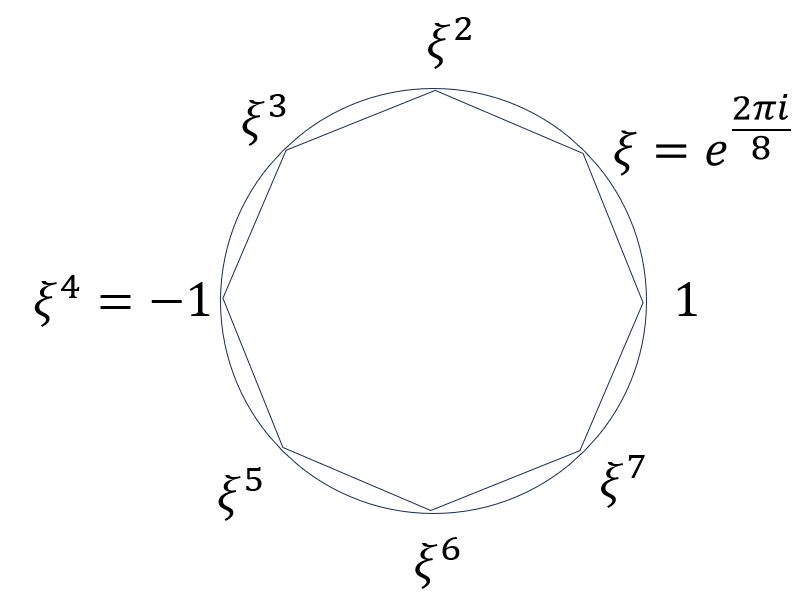
\xiの性質をいくつか確認しておきます。
-
\xiを、Mの半分N:=M/2乗すると-1。\xi^N=e^{\pi i}=-1.
-
N個の\xiの奇数乗、\xi, \xi^3, \xi^5, \dots, \xi^{2N-1}は全て互いに異なる。
-
(X-\xi)(X-\xi^3)\cdots(X-\xi^{2N-1})=\prod_{j=1}^N(X-\xi^{2j-1})=X^N+1である。
- なぜなら両辺の多項式はどちらもXのN次式、かつX^Nの係数は1であり、
- 左辺の多項式にX=\xi^{2j-1}を代入すると0。右辺の多項式も(\xi^{2j-1})^N+1=(\xi^N)^{2j-1}+1=(-1)^{2j-1}+1=-1+1=0.
- つまりN個の異なるX=\xi^{2j-1}を解に持つ。よって両辺の多項式は一致する。
多項式の集合からなる環
ℂを複素数体（複素数全体の集合）として、ℂ[X]を変数Xに関する複素数係数多項式全体とします。
多項式f(X)とg(X)に対して、多項式の和と差(f \pm g)(X):=f(X) \pm g(X)や積(fg)(X):=f(X)g(X)を定義できます。ただ、定数でない多項式の逆数（逆元）は多項式にはならないので割り算は定義できず、体にはなりません。このような加減乗算ができる集合を環(ring)といいます。
ℂのN次元ベクトル空間ℂ^Nもベクトルの各成分ごとに加減乗算することで環になります（0:=(0, \dots, 0)が加法に関する単位元、1:=(1,\dots, 1)が乗法に関する単位元です）。
\begin{align*}
(1, 2, 3, 4) + (5, 6, 7, 8) &= (6, 8, 10, 12),\\
(1, 2, 3, 4) \times (5, 6, 7, 8) &= (5, 12, 21, 32).
\end{align*}
さて、ℂ[X]から、ℂ^Nへの写像σを1のM乗根\xiを使って次のように定義します。
f(X)を多項式としたとき、f(X)のX=\xi^{2j-1}における値をN個並べたもの、つまり
σ: ℂ[X] \ni f \mapsto (f(ξ), f(ξ^3), \dots, f(ξ^{2N-1})) \in ℂ^N.
σは多項式の値を計算するだけなので、多項式 f, g に対して多項式の和f+gや積fgのX=aにおける値はf(a)+g(a)やf(a)g(a)です。つまり
- σ(f + g) = σ(f) + σ(g).
- σ(fg) = σ(f)σ(g).
群の場合は加法群なら上の式、乗法群なら下の式を満たすとき（群）準同型といいました。環は加算と乗算両方定義されているので両方成り立っているとき環準同型といいます。
なお、ℂ[X]の中でf(X)=0が加法に関する単位元、f(X)=1が乗法に関する単位元で、σによる行き先はそれぞれベクトル0=(0, \dots, 0)と1=(1, \dots, 1)です。
σの性質
σの性質をもう少し詳しく調べます。
σの全射性
f(X)を複素数係数N-1次多項式f(X)=\sum_{k=0}^{N-1} a_k X^kとすると、σ(f) = (\sum_{k=0}^{N-1} a_k (ξ^{2j-1})^k)_{j=1, \dots, N}.
a := (a_0, a_1, ..., a_{N-1})をN次元ベクトル、s_{kj}:=\xi^{(2j-1)k}, S:=(s_{kj})_{k=0,\dots,N-1, j=1,\dots, N}をN \times N行列、b:=σ(f)\in ℂ^NもN次元ベクトルとすると、b=aSと書けます（ベクトルと行列の掛け算）。つまりσはベクトルに行列Sを掛ける操作とみなせます。
SはVandermonde行列と呼ばれる行列で\xi, \xi^3, \dots, \xi^{2N-1}が全て異なるので逆行列が存在します。したがって、ℂ^Nの任意のbに対してa:=bS^{-1}とするとaS=b、つまりσ(a)=bとなるaが存在します。このような性質を持つσを全射であるといいます。
σのkernel
σの行き先が0になる多項式全体Ker(σ):=\Set{f\in ℂ[X] | σ(f)=0}をσの核(kernel)といいます。f \in Ker(\sigma)をとると、定義によりf(\xi)=f(\xi^3)= \dots =f(\xi^{2N-1})=0.
これはX=\xi^{2j-1}が方程式f(X)=0の解であることを意味します。つまりf(X)はX-\xi, X-\xi^3, \dots, X-\xi^{2N-1}で割り切れます。
この記事の最初の節で示したようにX-\xi, \dots, X-\xi^{2N-1}を全部掛けるとX^N+1だったのでf(X)はX^N+1で割り切れます。
つまりKer(σ)はX^N+1の倍数\Set{(X^N+1)g(X) | g(X) \in ℂ[X]}=(X^N+1)ℂ[X]です。
同型写像
R:=ℂ[X]/(X^N+1)をX^N+1で割った余りの多項式全体、つまりXについてのN-1次多項式全体とします。拡大体のときと同様、Rは多項式同士の普通の加減算、乗算後にX^N+1で割った余りをとることで乗算を定義できます。
任意の多項式f(X)について、X^N+1で割ったときの商をq(X), 余りをr(X)とするとf(X)=(X^N+1)q(X)+r(X)とかけ、余りの次数は最大N-1です。
このときσ(f)を考えるとX^N+1の部分が0になるのでσ(f)=σ(r)です。よって、今までの議論により
\tilde{σ}:R=ℂ[X]/(X^N+1) \ni r(X) \mapsto σ(r) \in ℂ^N
は1対1の対応です。そして環準同型でもあるので、環同型といいます。この対応によりRと複素N次ベクトル空間ℂ^Nを同一視できます。この同一視では多項式同士の加減乗算が、ベクトル同士の加減乗算に対応します。
※（数学の人向け） σ:ℂ[X] \rightarrow ℂ^Nが全射で環準同型で、Ker(σ)=(X^N+1) ℂ[X]なので、同型写像\tilde{σ}:R=ℂ[X]/(X^N+1) \rightarrow ℂ^Nが誘導されます。
まとめ
多項式をX^N+1で割った余りとN次元ベクトル空間を同一視する方法を紹介しました。多項式の加減乗算はベクトルの要素ごとの加減乗算に対応します。
次回、この対応を用いてベクトル空間の平文を多項式で表示する方法を紹介します。
Discussion