準同型暗号CKKSその2 エンコードとデコード

初めに

前回、多項式環とベクトル空間の同型対応を紹介しました。今回はそれを使ってCKKSの平文空間、およびエンコード・デコードという処理を紹介します。

前回の復習

$M$を4以上の2のべきの形の整数、$\xi:=e^{2\pi i/M}$, $N:=M/2$としたとき$σ:ℂ[X]/(X^N+1) \rightarrow ℂ^N$を$σ(f):=(f(\xi), f(\xi^3), \dots, f(\xi^{2N-1}))$で定義し、それが環同型となっていることを示しました。$ℂ[X]/(X^N+1)$は$N-1$次以下の多項式の集合と同一視しておきます。

複素共役

複素数$z=a+bi$（$a,b \in ℝ）$に対して、複素共役（きょうやく）を$conj(z):=a-bi$と書きます。複素共役は複素平面の$x$軸に対する線対称の操作です。markdownでチルダ$\tilde{z}$は表記しづらいので$conj$を使います。
複素数$z$, $w$の和や積の複素共役はそれぞれの複素共役です。

$$\begin{align*} conj(z+w)&=conj(z)+conj(w),\\ conj(zw)&=conj(z)conj(w). \end{align*}$$

実数$a$の複素共役は変化しません。

$$conj(a)=a.$$

さて、$\xi$について$conj(\xi)=\xi^{M-1}$です。よって$conj(\xi^u)=\xi^{M-u}$です。
前回の1の8乗根の例を見ても、

$$\begin{align*} conj(\xi)&=\xi^7,\\ conj(\xi^2)&=\xi^6,\\ conj(\xi^3)&=\xi^5,\\ conj(\xi^4)&=\xi^4 \end{align*}$$

を確認できます。

実数係数多項式環

$f$が実数係数多項式なら$conj(f(\xi^{2j-1}))=f(conj(\xi^{2j-1}))=f(\xi^{M-2j+1})$です。だから$σ(f)=(f(\xi^{2j-1}))_{j=1,\dots,N}$は$N$次元ベクトルですが、後半$N/2$個の要素は前半の$N/2$個の要素を逆順にして複素共役をとったものです。つまり情報としては前半の$N/2$個で十分です。

実係数多項式$f$についての$σ(f)$

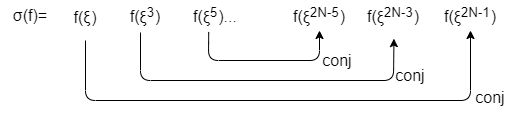
逆に、一般の複素数係数多項式$f \in ℂ[X]/(X^N+1)$が
条件(real-cond) : $conj(f(\xi^{2j-1}))=f(\xi^{M-2j+1})$ for $j=1,\dots,N/2$
を満たすと$f \in ℝ[X]/(X^N+1)$です。
なぜなら任意の$f(X) \in ℂ[X]/(X^N+1)$は、ある実数係数多項式$g, h \in ℝ[X]/(X^N+1)$を使って$f(X)=g(X)+ih(X)$と書けます。$t:=2j-1$とすると、

$$conj(f(\xi^t))=conj(g(\xi^t)+ih(\xi^t))=g(\xi^{M-t})-ih(\xi^{M-t}).$$

ここで条件(real-cond)より

$$conj(f(\xi^t))=f(\xi^{M-t})=g(\xi^{M-t})+ih(\xi^{M-t}).$$

両者が等しいので$h(\xi^{M-t})=0.$ 複素共役をとれば$h(\xi^t)=0.$ これが$t=1,3,\dots,N-1$で成り立つので$h(X)=0.$ これは$f \in ℝ[X]/(X^N+1)$を意味します。

そこで、$ℂ^N$の前半だけを取り出す写像を定義します。

$$π: ℂ^N \ni (z_1, \dots, z_N) \mapsto (z_1, \dots, z_{N/2}) \in ℂ^{N/2}.$$

この逆写像は一意には決まりませんが、前半分から後ろ半分を逆順の複素共役で復元する写像を

$$π^{-1}: ℂ^{N/2} \ni (z_1,...,z_{N/2}) \mapsto (z_1,...,z_{N/2}, conj(z_{N/2}), .., conj(z_1)) \in ℂ^N$$

と定義します。すると先程の議論により$σ(ℝ[X]/(X^N+1))$の要素は条件(real-cond)を満たし、逆に条件(real-cond)を満たす$f \in ℂ[X]/(X^N+1)$は$f \in ℝ[X]/(X^N+1)$なので$H:=π^{-1}(ℂ^{N/2}) \subseteq ℂ^N$とすると$σ(ℝ[X])=H$です。
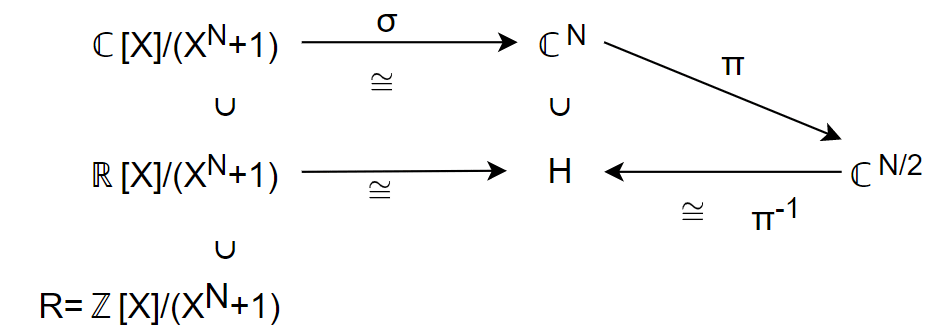
関係がややこしくなったので図示すると

$ℂ[X]$と$ℝ[X]$の関係

CKKSの平文空間とエンコード・デコード

ようやくCKKSの平文空間を定義する準備が出来ました。$R:=ℤ[X]/(X^N+1)$とします。$R$は整数係数多項式を$X^N+1$で割った余りの集合です。$R$がCKKSの平文空間です。
実はCKKSは厳密な準同型暗号ではなく、近似準同型暗号というもので、暗号化して復号すると元の値から少しずれます。加算や乗算でも誤差がでます。
暗号化する準備で発生する誤差を制御するための値をスケール因子$Δ$といいます。小数$x$を整数に丸めたものを$[x]$と書き、より一般に多項式$f$の各係数を整数に丸めたものも$[f]$と書くことにします。
暗号化したい複素$N/2$次元ベクトル$z \in ℂ^{N/2}$をとり、$f:=σ^{-1}(\pi^{-1}(z))$とします。前節の図で右端の要素を左端の空間に持ってきます。
$f$は実数係数多項式で、それをスケール因子$Δ$倍して係数を整数に丸めたもの$[Δf] \in R$を得る操作をエンコードといいます。

$$Ecd : ℂ^{N/2} \ni z \mapsto [Δσ^{-1}(\pi^{-1}(z))] \in R=ℤ[X]/(X^N+1).$$

逆に平文空間$R$の多項式$f$に対して$\pi(σ(Δ^{-1}f)) \in ℂ^{N/2}$を得る操作をデコードといいます。

$$Dcd : R=ℤ[X]/(X^N+1) \ni f \mapsto \pi(σ(Δ^{-1}f)) \in ℂ^{N/2}.$$

エンコードとデコードは扱いたい$N/2$次元ベクトルをCKKSの平文空間$R$に移したり、元に戻したりする操作であって、暗号化・復号ではないことに注意してください。
また、エンコードの際に丸め処理が入っているのでエンコードしてデコードしても完全に元に戻るとは限らないことにも注意してください。スケール因子$Δ$を大きくとれば、その誤差を小さくできます。

まとめ

CKKSの平文空間$R=ℤ[X]/(X^N+1)$を定義しました。$ℂ^{N/2}$と実数係数多項式の集合$R=ℤ[X]/(X^N+1)$との関係を調べ、それらの間を行ったり、来たりするエンコードとデコードを定義しました。