🕌

FunctorチュートリアルとBiinvariant Opticsへの展望

2025/12/17に公開

Haskell

idea

はじめに/ロードマップ

関数型言語の一部にはモナドっていう、難しくて、人々が苦しんでて、わかった暁にはかならずチュートリアルを書きたくなるものがあるらしいですね。

この記事はモナドチュートリアルではありません。

個人的には難しいのってモナド自体というよりむしろ、仰々しい名前のついたフワッとした抽象、特に高階型まわりのあれやこれや、というジャンルだと思っています。

その代表例で、まだシンプルなやつであるFunctorというのがあります。

前半は、ゆっくりとFunctorのチュートリアルを行います。
だんだんギアをあげて隣接する概念に手を伸ばし、今アツい概念であるProfunctor Opticsや、その拡張であり、名前がついてなさそうなので個人的にBiinvariant Opticsと呼んでいるものまでを滑らかに語れればいいなと思っています。

コード例は都合の良さからHaskellで示していますが、Haskellを見慣れていない人のためにも比較的読みやすいコードをたくさん置きました。

1階型/1-variantness

Functor

V2

平易なものからはじめます。

V2という型があります。

data V2 a = V2 a a

こんな形をしています。aにIntを入れて(Int,Int)を作ったりDoubleを入れたりして2次元座標を表す目的で使う型ですが、2次元座標のつもりでなくても任意の(非高階)型aの要素2つをもったデータを表すことができます。

高階型とカインド

非高階型とは言いましたが、多くのプログラミング言語で"型"と言われているもののことで、Haskellでは「Typeカインドの型」「*カインドの型」と言います。名前が複数あるのは歴史的事情です。この記事ではTypeとします。
「Typeカインドの型」というからには他のカインドの型もありそうな言い回しですよね。一つの例が、V2のように1つTypeの型名を入力するとTypeの型になる、Type -> Typeカインドの型です。言語によっては"型変数1つをとるジェネリクス型"でしょうか？
Nimではこうですね。

type V2[A] = tuple[x, y: A]

カインドという言葉を多用しますが、高階型を含めた型の分類くらいの意味です。あとで補足するかもしれません。
納得してから行きたいという人には次の記事がおすすめです。

ここでV2 Int -> V2 Doubleという型の関数を考えてみましょう。

例

i2d :: Int -> Double
i2d = fromIntegral

-- ひっくり返して半分
swapAndHalf :: V2 Int -> V2 Double
swapAndHalf (V2 x y) = V2 (i2d y / 2) (i2d x / 2)

-- 相加平均と相乗平均
averages :: V2 Int -> V2 Double
averages (V2 x y) = V2 (i2d (x + y) / 2) (sqrt (i2d (x * y)))

-- 単純に両辺をキャストするだけ
vi2vd :: V2 Int -> V2 Double
vi2vd (V2 x y) = V2 (i2d x) (i2d y)

-- 引数を無視して原点を返す
constOrigin :: V2 Int -> V2 Double
constOrigin _ = V2 0 0

-- ...

無数にあります。

文字(Unicodeコードポイント)の型Charとその単方向連結リストの型Stringに対するV2 Char -> V2 Stringを考えたときにも、あらゆる煮たり焼いたりが可能そうなことが想像できます。

-- 単一文字からなる無限文字列の組 
-- 無限リストを生成するrepeat関数が標準ライブラリにあるの本当に無法で好き
infiniteStrings :: V2 Char -> V2 String
infiniteStrings (V2 x y) = V2 (repeat x) (repeat y)

ここまで挙げた関数はどれもV2に食わせた中身の型の特徴を利用していました。
fromIntegral, (+), (*), (/), repeatなど。

ここで任意の型aとbについてV2 a -> V2 bという関数を作ることを考えます。

mapV2 :: V2 a -> V2 b
mapV2 (V2 x y) = ...

どうですか？中身の特徴を用いないとまともな手段では書けなくなりますね。~~まともでない手段としてはUnsafeCoerceなどがあります。~~
aからbへの変換、a -> b型の関数が与えられればV2 a -> V2 bを書けそうです。

余談

ちなみにHaskellではこの手の任意の型をとる抽象的な関数が異様に簡潔な表記法で書けます。型名のところに小文字でなんか書くだけです。

mapV2 :: (a -> b) -> V2 a -> V2 b
mapV2 f (V2 x y) = V2 (f x) (f y)

なんか綺麗でいいですね。なんか綺麗というのは、具体的には\a -> aというパススルーをする関数をfに入れたときに全体が\(V2 x y) -> V2 x yというパススルーになってたり、関数合成演算子(.)を使って書くとmapV2 f . mapV2 gがmapV2 (f . g)と等しくなったりという性質の良さです。^[1]

mapなんちゃら

V2以外についても同じように中身の特徴を見ないで変換する関数を書きます。^[2] ^[3] ^[4] ^[5] ^[6]

例

-- aが1個、というかaそのもの
newtype Identity a = Identity {runIdentity :: a}

mapIdentity :: (a -> b) -> Identity a -> Identity b
mapIdentity f (Identity a) = Identity (f a)

-- 0個か1個
data Maybe a = Nothing | Just a

mapMaybe :: (a -> b) -> Maybe a -> Maybe b
mapMaybe _ Nothing = Nothing
mapMaybe f (Just a) = Just (f a)

-- eかもしれない
data Either e a = Left e | Right a

mapEither :: (a -> b) -> Either e a -> Either e b
mapEither _ (Left e) = Left e
mapEither f (Right a) = Right a

-- なんかくっついてる
mapTuple :: (a -> b) -> (w, a) -> (w, b)
mapTuple f (w, x) = (w, (f x))

-- rをとってaを返す関数(r -> a)
newtype Reader r a = Reader {runReader :: r -> a}

mapReader :: (a -> b) -> Reader r a -> Reader r b
mapReader f (Reader x) = Reader (\r -> f (x r))

-- Readerと同じように関数(r -> a)もmapできる
mapFn :: (a -> b) -> (r -> a) -> (r -> b)
mapFn ab ra r = ab (ra r)

-- 2分木
data Tree a = TLeaf a | TNode (Tree a) (Tree a)

mapTree :: (a -> b) -> Tree a -> Tree b
mapTree f (TLeaf a) = TLeaf (f a)
mapTree f (TNode l r) = TNode (mapTree f l) (mapTree f r)

-- 素朴なfinger tree
data FT a = Empty | Single a | Deep (Digit a) (FT (Node a)) (Digit a)
data Digit a = One a | Two a a | Three a a a | Four a a a a
data Node a = Node2 a a | Node3 a a a 

mapDigit :: (a -> b) -> Digit a -> Digit b
mapDigit f (One x) = One (f x)
mapDigit f (Two x y) = Two (f x) (f y)
mapDigit f (Three x y z) = Three (f x) (f y) (f z)
mapDigit f (Four x y z w) = Four (f x) (f y) (f z) (f w)

mapNode :: (a -> b) -> Node a -> Node b
mapNode f (Node2 x y) = Node2 (f x) (f y)
mapNode f (Node3 x y z) = Node3 (f x) (f y) (f z)

mapFT :: (a -> b) -> FT a -> FT b
mapFT _ Empty = Empty
mapFT f (Single a) = Single (f a)
mapFT f (Deep l x r) = Deep (mapDigit f l) (mapFT (mapNode f) x) (mapDigit f r)

これらはa -> bがあればf a -> f bが書けるType -> Typeカインドの型fだということができます。

型クラス

この型ごとに名前が異なるよく似た関数で名前空間を埋め尽くすの気に入りませんね。まあそういう抽象的なものをまとめるのプログラマーは好きなので様々な言語でinterfaceとかtraitとかconceptとかprototypeとかいろいろな切り口の言語機能が提供されていますが、Haskellでは"型クラス(type class)"でやります。

Semigroupという型クラスを例に挙げます。

class Semigroup a where 
  (<>) :: a -> a -> a

半群...閉じた加算が結合則を満たす...というとブラウザバックされるかもしれませんが、要するに右から左からくっつけられるTypeカインドの型を表す型クラスが、Semigroupです。

連結リストでの実装はこのように書かれています。

instance Semigroup [a] where 
  (<>) = (++)

(++)はリスト同士を連結するリスト専用の関数です。

余談

Semigroup, Monoidクラスの具体的な勘所についてはこの記事がかなり効きます。

SemigroupのようにTypeカインドの型に対する抽象はたいていのモダンな言語で容易に書けると思います。

import sequtils

type 
  Semigroup = concept x, type t
    x.sappend(x) is t

proc sappend[T](x, y: seq[T]): seq[T] = x.concat y

proc stimes[T: Semigroup](n: int, t: T): T =
  result = t
  for _ in 1..<n:
    result = result.sappend t
    
when isMainModule:
  assert 3.stimes(@['a']) == @['a', 'a', 'a']

少なくともNimは余裕ですね。

問題はType->Typeカインドの型の場合で、たいていの言語で頑張ることになります。^[7]
頑張るのって説明のノイズなので、今回は言語仕様のおかげで頑張らなくていい言語のひとつであるHaskellで話を進めます。

Functorクラス

先程の"a -> bがあればf a -> f bが書けるf"のことを、Haskellの標準ライブラリbaseではFunctorという名前の型クラスで表現しています。標準ライブラリbaseにあります。嬉しい言語です。

class Functor f where
  fmap :: (a -> b) -> f a -> f b

なので上記の例に上げたmapなんちゃらという関数はわざわざmapなんちゃらという名前をつけなくても、

instance Functor (Either e) where
  fmap f (Right a) = Right (f a)
  fmap _ (Left e) = Left e

というふうに書くことで名前がfmapひとつで済むということですね。

いまやすべてのFunctorに適用できる関数を書くこともできるようになりました。^[8]

hylo :: Functor f => (f b -> b) -> (a -> f a) -> a -> b
hylo f g = h where h = f . fmap h . g

hyloが気になる人のために軽く紹介

例えばなにかしらコレクションがあってそれを走査したいとします。
"全体の長さを取得して、ループカウンタを宣言して、for文で回しつつカウンタをインクリメントする"というのは、間違ってないけど(無限ループになって停止しないなど)境界でいくらでも事故りそうな手続きです。
そこへモダンなプログラミング言語だとイテレータをイテレートするというナイスな代替手段を持っていることが多いですよね。
アナロジー。
なにかしら再帰を起こす関数を書きたいとします。
直接に再帰を書いても間違いではないのですが、(無限再帰になって停止しないなど)境界でいくらでも事故りうるうえに、コンパイル最適化の妨げになるなどの難があります。
recursion schemeというゴツい概念があって、生の再帰に対する代替手段です。研究途上です。
イテレータが内部的には結局ループカウンタを持ってインクリメントしてることがあるのと同様に、recursion schemeも結局のところ内部的には再帰しているのですが、イテレータを使うと陽にインクリメントしなくていいように、recursion schemeを使うと陽に再帰しなくてよくなります。
hyloはこのひとつで、気持ちとしてはイテレータ生産とイテレータ消費って打ち消しあって中間データ不要になるよね？というものです。難しいので興味があれば突っ込んでみてください。

そして、これが標準ライブラリbaseにあることで、他のライブラリの作者も追随して、Functorのインスタンスになりそうな型がたいていそのようになっています。治安が良いですね。

加えて、後述の変なことをしない限りたいていのType -> Type型はFunctorになるということ、その実装は型の構造から一意に導出できることが知られており、GHCでは自動で書いてくれる機能すらあります。

-- rose tree
data Rose a = Rose a [Rose a] deriving (Functor)
-- ↑ これでinstance Functor Rose where fmap = 以下略 も書いたことになり、震える

Applivative, Alternative, Monad, Comonad, Traversableなどさまざまな型クラスの親となることもあって、この粒度の抽象がドシッと言語の中枢に据わっています。嬉しいですね。

そのへんの話は世のモナドチュートリアルに譲ります。
モナドチュートリアルで検索するとたくさん記事が出てきますが、正直「仰々しい名前の高階型の型クラスでフワッとしたやつを理解することの難しさ」以上の困難は特にないと信じています。

	型クラス	めあて
1	`Semigroup`	仰々しい名前のフワッとした型クラスを理解する。
2	`Functor`	仰々しい名前のついた高階型の型クラスでフワッとしたやつに慣れ親しむ。

というのが近道だと思っています(そこまでやればMonadとかも書いてあるまんま読めばいいので)。

Functor概念がある言語はHaskellだけではないので、すでに慣れ親しんでいる人は退屈だったかもしれませんが、個人的には引っかかりの多い場所だろうと思ったので丁寧にやりました。
ここからはあんまり日本語で記事になってない話をします。

Functor以外

"後述の変なこと"、すなわちFunctorにならないType -> Typeカインドの型についてという本題です。本題なんですが、ここまで丁寧にやったぶん加速していきます。

Contravariant

これらの型はFunctorになりません。^[9] ^[10] ^[11]

newtype Predicate a = Predicate {getPredicate :: a -> Bool}
newtype Comparison a = Comparison {getComparison :: a -> a -> Bool}
newtype Op r a = Op {getOp :: a -> r}

Functorというのはf a -> f bを得るためにa -> bが必要な型でしたが、これらは引数と返り値がひっくり返ったb -> aを与えることでf a -> f bが作れます。

そのような型のための型クラスがContravariantです。^[12]

class Contravariant f where
  contramap :: (b -> a) -> f a -> f b

Functorを理解したみなさんには何も難しいことないですね。インスタンスの実装を演習問題にしてもいいくらいです。解答はhackageのsourceのところに書いてあります。

Contravariantという名前について

Functorという名前は数学の圏論という分野由来なんですが、HaskellのFunctor型クラスは圏論の関手(functor)そのものではなくて、"Hask圏における共変自己関手(Covariant Endo-functor)"のことです。僕は数学に自信がないので詳しい解説は有識者の方に譲りますが、Covariantの対義語がContravariant(反変)です。
fmap :: (a -> b) -> f a -> f b
contramap :: (b -> a) -> f a -> f b
対義っぽさ。Contravariantの人たちも圏論的な意味ではfunctorだそうです。ちょっとかわいそうな感じがしないでもないですが。

Invariant

そしてFunctorにもContravariantにもならないType -> Typeカインドの型もあります。 ^[13]

newtype Endo a = Endo {appEndo :: a -> a}

a -> bだけでもb -> aだけでもEndo a -> Endo bすなわち(a -> a) -> b -> bを作ることはできなくて、その両方が要求されます。

これをやるための型クラスは流石にbaseには入ってなくて、invariantパッケージのInvariantというのがあります。^[14]

class Invariant f where
  invmap :: (a -> b) -> (b -> a) -> f a -> f b

instance Invariant Endo where
  -- invmap :: (a -> b) -> (b -> a) -> Endo a -> Endo b
  invmap ab ba (Endo aa) = Endo (\b -> ab (aa (ba b))

他のプログラミング言語では

ScalazのInvariantFunctor(xmap), CatsのInvariant(imap)と同じです。Purescriptにもpurescript-invariantがあるな。僕がScala書かないのでHaskellで記事書いちゃってるけどこっちのほうが型クラス階層しっかりしててよかったかもしれないです。Ocamlにあるかどうかはググってもわかりませんでした。

この概念これから大切なのでもうひとつくらいオリジナル例を作りましょう。
Functorな(->)(関数)とContravariantなOpを1つの型が同時に持っちゃうとどちらも必要になります。

data s <-> t = Isomorphism (s -> t) (t -> s)
instance Invariant ((<->) s) where
  -- invmap :: (a -> b) -> (b -> a) -> (s <-> a) -> (s <-> b)
  invmap ab ba (Isomorphism sa as) = Isomorphism (\s -> ab (sa s)) (\b -> as (ba b))

この表記、何か変……？

Haskellでは、型と値はなるべく同じようなルールで表記できるように設計されています(嬉しい)。
関数と演算子についてはこちらをご参照ください。

これら関数(及び演算子)もまた(関数)型です。
(アナロジー)
おなじように、2つ以上型パラメータを取る高階型は、バッククオートで中置できるし、ユーザ定義の演算子でもいいし、演算子ならカッコで囲むと前置になるし、そして、型です(嬉しい)。^[15]

data (:*:) (f :: k -> Type) (g :: k -> Type) (p :: k) = f p :*: g p

あと型構築子(型宣言の右辺にあるやつ)は、型名と一致しなくてもいいです。一致を求めると直和型が書けなくなるというのもありますが、この(<->)とIsomorphismの例のようにめっちゃ違ってても(名前空間がかさばって不親切であるという点を除いては)構わないです。^[16] ^[17] ^[18] ^[19]

data (a :: k) :~: (b :: k) where
  Refl :: a :~: a

data Cofree f a = a :< f (Cofree f a)

data (:+:) (f :: k -> Type) (g :: k -> Type) (p :: k) = L1 (f p) | R1 (g p)

data Complex a = !a :+ !a

余談ですが、値と型の関係のアナロジーで型の分類をカインドでやっている、という理解ができるようになります。型注釈と同じ::という記号でカインドを注釈しています。嬉しいですね。

既存のライブラリにおける`(<->)`型

ここでの(<->)型はsemigroupoidsライブラリのData.IsomorphismのIsoをつかってIso (->)としたものやinvertibleライブラリのData.Invertible.BijectionのところにあるBijection (->)および(<->)と同一です。
概念として重要なので絶対に先駆者がいます。少なくとも記号は自分で考えたんですけど、(->)との対比がきれいになって、かつ見た目で意味が伝わるような記号となると収斂してくるものですね。この記事を書いててはじめてinvertibleライブラリ見たんですけど、ほんとうに偶然の一致です。怖い。
まあただこれらのライブラリはちょっとこの記事の説明には過剰な抽象化がなされているため、今回はこうして触れるにとどまります。いうても(->)がパラメータ化されてkになってるだけなんですけど。

同型について

数学のことばで同型(isomorphic)というものがあって、等しさを緩めたやつです。

ざっくり言います。

例として十二支と遊戯王の十二獣モンスターを考えます。

https://yugioh-wiki.net/index.php?������


十二支
十二獣


子
《十二獣モルモラット》

丑
《十二獣ブルホーン》

寅
《十二獣タイグリス》

卯
《十二獣ラビーナ》

辰
《十二獣ドランシア》

巳
《十二獣ヴァイパー》

午
《十二獣サラブレード》

未
《十二獣ラム》

申
《十二獣ハマーコング》

酉
《十二獣クックル》

戌
《十二獣ライカ》

亥
《十二獣ワイルドボウ》

十二獣モンスターは十二支そのものではありませんが、十二支との間には、モチーフになった干支: 十二獣モンスター \rarr 十二支 と この干支をモチーフとする十二獣モンスター: 十二支 \rarr 十二獣モンスター という2つの関係があり、十二支と十二獣モンスターが一対一対応を持っているためこの2つを合成しても一切情報を落とさず戻ってくることができます。
一般に対象AとBが同型である(isomorphic)とは、f: A \rarr B, g: B \rarr Aという2つの写像(射)があって、その合成fg, gfがgf=1_A,fg=1_Yを満たすことです。(1_A,1_BをそれぞれA,Bにおける恒等写像(恒等射)とします。)。fを同型写像/同型射(Isomorphism)といい、gをその逆射といいます。あるいは逆。という説明でわかった人で遊戯王を知らない人は遊戯王wikiを見なくてもいいです。あるいは十二支と\Z/12の関係に置き換えてください。

十二支	十二獣
子	《十二獣モルモラット》
丑	《十二獣ブルホーン》
寅	《十二獣タイグリス》
卯	《十二獣ラビーナ》
辰	《十二獣ドランシア》
巳	《十二獣ヴァイパー》
午	《十二獣サラブレード》
未	《十二獣ラム》
申	《十二獣ハマーコング》
酉	《十二獣クックル》
戌	《十二獣ライカ》
亥	《十二獣ワイルドボウ》

a <-> b型はaとbが同型であると主張することに使えることがわかります。^[20]この記事の後半で使います。

Omnivariant

InvariantはFunctorでもContravariantでもないType->Typeカインドの型でしたが、逆に、FunctorかつContravariantであるようなfはf a -> f bを書くためになにが必要でしょうか。

答えはbaseのphantom関数にあります。

phantom :: (Functor f, Contravariant f) => f a -> f b
phantom x = () <$ x $< ()

-- 補足 `base`での実装にはconst関数とかがでてきてやさしくないので書きなおしています。
(<$) :: (Functor f) -> a -> f b -> f a
a <$ x = fmap (\(_ :: b) -> a)

($<) :: (Contravariant f) -> f b -> b -> f a
x $< b = contramap (\(_ :: a) -> b)

()は()という値のみを持つ型です。zenですね～。(<$)も($<)も左結合の演算子なので、x :: f aに対して() <$ xとやってf ()型を得て、( (() <$ x) :: f ()) $< ()の結果がf bになります。

先ほどとうって変わってa -> bもb -> aも要りません。一体どんな型がFunctorかつContravariantなのか、ツラを拝みたくなりますね。^[21] ^[22] ^[23]

data Proxy a = Proxy

instance Functor Proxy where 
  fmap _ _ = Proxy

instance Contravariant Proxy where
  contramap _ _ = Proxy

newtype Const r a = Const { getConst :: r }

instance Functor (Const r) where
  fmap _ (Const r) = Const r

instance Contravariant (Const r) where
  contramap _ (Const r) = Const r
  
newtype Clown f x a = Clown { runClown :: f x }

instance Functor (Clown f x) where
  fmap _ (Clown fx) = Clown fx

instance Contravariant (Clown f x) where
  contramap _ (Clown fx) = Clown fx

a -> bもb -> aも使ってないことがわかります。それどころかa型に関連するものがなにも入っていません。なにもしない計算を2回もやるのってもったいないので型クラスにしてしまいましょう。

class Omnivariant f where
  omnimap :: f a -> f b
  default omnimap :: (Functor f, Contravariant f) => f a -> f b
  omnimap = phantom

例えばProxyの2階バージョンDaydraemなんてものをでっち上げてみましょう(あとで使います)。

-- a も b も無視する
data Daydream a b = Daydream

instance Omnivariant (Daydream x) where
  omnimap _ = Daydream

instance Functor (Daydream x) where
  fmap _ _ = Daydream

instance Contravariant (Daydream x) where 
  contravariant _ _ = Daydream

instance Invariant (Daydream x) where
  invmap _ _ _ = Daydream

1-variantness

このようにしてaやbの具体的な性質に言及せずにf a -> f bを得るための型クラスが4つ出揃いました。
表にまとめましょう。

	`a -> b`	`b -> a`
Invariant	必要	必要
Functor(Covariant)	必要	不要
Contravariant	不要	必要
Omnivariant	不要	不要

a -> bとb -> aそれぞれが必要か不要かによって4通りあるという景色があります。

ここで、

invmap :: Invariant f => (a -> b) -> (b -> a) -> f a -> f b
invmap' :: Invariant f => (a <-> b) -> f a -> f b

omnimap :: Omnivariant f => f a -> f b
omnimap' :: Omnivariant f => Daydream a b -> f a -> f b

contramap :: Contravariant f => (b -> a) -> f a -> f b
contramap' :: Contravariant f => Op a b -> f a -> f b

という変形をしても、

invmapIso :: ((a -> b) -> (b -> a) -> f a -> f b) <-> ((a <-> b) -> f a -> f b)
invmapIso = Isomorphism (\f (Isomorphism g h) -> f g h) (\f g h -> f (Isomorphism g h))

omnimapIso :: (f a -> f b) <-> (Daydream a b -> f a -> f b)
omnimapIso = Isomorphism (\f Daydream -> f) (\f -> f Daydream)

contramapIso :: ((b -> a) -> f a -> f b) <-> (Op a b -> f a -> f b)
contramapIso = Isomorphism (\f (Op g) -> f g) (\f g -> f (Op g))

という同型関係があるため構わないことがわかります。

変形後のコードの第一引数を見てみましょう。

型クラス	関数	第一引数
Invariant	invmap'	(<->) a b
Functor	fmap	(->) a b
Contravariant	contramap'	Op a b
Omnivariant	omnimap'	Daydream a b

p a bという形に揃いましたね。しかもp aが綺麗に左端の型クラスのインスタンスになっています。
一般化の時間です。

-- FunctionalDependenciesとかいくつかのGHC拡張が必要な書き方。GHC拡張なんぞやついてはここでは扱いません。
class (forall a. k (p a)) => Variantness k p | k -> p, p -> k where
  genVariant :: (k f) => p a b -> f a -> f b

p aが型クラスkのインスタンスであるとき、pをつかってなんちゃらmapをgenVariantで書き換えられるという関係の、kとpが一対一対応である……くらいの意味合いなんですが、記号が多くなってきてイカツいですね。
イカツいときには具体的なインスタンスを書いて脈を落ち着かせましょう。

instance Variantness Invariant (<->) where
  genVariant :: Invariant f => (a <-> b) -> f a -> f b
  genVariant (Isomorphism f g) = invmap f g

instance Variantness Functor (->) where
  genVariant :: Functor f => (a -> b) -> f a -> f b
  genVariant = fmap

instance Variantness Contravariant Op where
  genVariant :: Contravariant f => Op a b -> f a -> f b
  genVariant (Op f) = contramap f

instance Variantness Omnivariant Daydream where
  genVariant :: Omnivariant f => Daydream a b -> f a -> f b
  genVariant Daydream = omnimap

Invariant, Covariant, Contravariant, Omnivariantをまとめた呼び方がググってもググってもでてこないので、個人的に1-variantnessと命名しました。日本語訳はまだ考えていません。^[24]

semi-optics

これまでf a -> f bを生み出すための条件の話ばかりしていて、f a -> f bそのものについてはあまり話をしていませんでした。
いっぱい書くのもスマートじゃないので型エイリアスをつけます。

type Semioptic f s a = f a -> f s

この記事では以降このSemioptic f s aの形でかけるものを総称してsemi-opticsと呼びます。

ツッコミたいことはたくさんあるとおもいます。
「opticsとは何でsemi-opticsは何が何のどう半分なんだ」
「opticsは聞いたことあるけどsemi-opticsなんて聞いたことないぞ、造語か？」
「f a -> f sって書くより長いじゃねえか」
「いままでずっとaとbでやってきたのにいきなりsなんて書いてどういう了見なんだ」
「そもそもなんのために右辺と左辺でaとsの順番を入れ替えてるんだ」
申し訳ありませんが、後述します。型エイリアスは都合の良さのためにつけるものなので、都合のよさについて述べなければなりません。

いくつかはここで答えられます。
semi-opticsは僕の造語です。opticsは既存のものです。

既存のものであるOpticにそろえてaとbではなくaとsという書き方にしていて、右辺と左辺のaとsを入れ替えています。

脱線しました。使用例として、Variantness型クラスを書き換えましょう。

class (forall a. k (p a)) => Variantness k p | k -> p, p -> k where
  genVariant :: (k f) => p a s -> Semioptic f s a

利用

なんとかmapあるいはgenVariantによって得られたSemioptic f s aの消費について考えます。

fに具体的なType -> Typeカインドの型を入れて様子を見てみましょう。

-- `base`にある、任意の型に対するパススルー関数
id :: x -> x
id x = x

review' :: Semioptic Identity s a -> a -> s
review' l a = runIdentity (o (Identity a))

view' :: Semioptic (Op a) s a -> s -> a
view' l = getOp (o (Op id)) 

views' :: Semioptic (Op r) s a -> (a -> r) -> s -> r
views' l f = getOp (o (Op f))

over' :: Semioptic Endo s a -> (a -> a) -> s -> s
over' l f = appEndo (l (Endo f))

onProduct' :: Semioptic ((,) w) s a -> w -> a -> (w -> s -> r) -> r
onProduct' l w a f = let (w', s) = l (w, a) in f w' s

onSum' :: Semioptic (Either e) s a -> Either e a -> (e -> r) -> (s -> r) -> r
onSum' l ea er sr = case l ea of 
  Left e -> er e
  Right s -> sr s

Semioptic なんたら s a ->の右側にある型に注目すると、急に実用的な香りがしてきます。
どんどん抽象に行くんじゃないのと思っていた方には肩透かしかもしれませんが、この香りはどちらかというと抽象化が汎用性という側面を研いだことによる恩恵です。

クラスベースOOPにおけるゲッターっぽい雰囲気を漂わせるreview'やview'、コールバックメソッドっぽい顔ぶれのviews'、更新メソッドっぽいover'など。

この記事で仙人みたいな気持ちになるのは浅いです。俗世のギラツキを忘れないでください。
徹頭徹尾、実用的なプログラミングの話をしています。
この記事と相性のいい、いわば近道の言語のひとつであるHaskellでやっているだけで、HKTをエミュレートするなどのところから頑張るとたいていの言語で実装することができます。言語固有の話ではありません。

Semioptic f s aを作る際には、どの型クラスを通じて作ったかによってfに入れられるType -> Typeが制限されます。その制限は、型クラスに書いてあるちょうどそのままです。
Semioptic fはゲッターや更新メソッドになったりならなかったりする計算の一般化で、Type -> Typeカインドの型fにかけられた型クラスによってどれになるかならないかが決まります。
そしてこれらsemi-opticを消費する関数においては、aやsが具体的にどんな型でどのような性質をもっているかに言及していません。どちらがwrapperでcontentなのかとか一切論じずに、ゲッターや更新を書けます。

ギラギラしてきましたか？ギラギラしてきましたね。

生成

消費の話をしていました。逆にSemioptic f s aのaとsに具体的な型を入れたものを作ることを考えます。
genVariant関数で統一的に作りましょう。

例

Omnivariant

oV2Int :: Omnivariant f => Semioptic f (V2 Int) Int
oV2Int = genVariant Daydream

oStrChar :: Omnivariant f => Semioptic f String Char
oStrChar = genVariant Daydream

退屈ですね。Omnivariant なら任意のaとsについて同じように書けます。

oArbitary :: Omnivariant f => Semioptic f s a
oArbitary = genVariant Daydream

ここからはそうではありません。
Contravariant

cV2IFirst, cV2ISecond, cV2ISum :: Contravariant f => Semioptic f (V2 Int) Int
cV2IFirst = genVariant (Op (\(V2 x _) -> x))
cV2ISecond = genVariant (Op (\(V2 _ y) -> y))
cV2ISum = genVariant (Op (\(V2 x y) -> x + y))

cStrHead :: Contravariant f => Semioptic f String (Maybe Char)
cStrHead = genVariant (Op (\s ->
  case s of
    (a:_) -> Just a
    _ -> Nothing)))

Functor

fV2IDup, fV2IX0, fV2I0Y :: Functor f => Semioptic f (V2 Int) Int
fV2IDup = genVariant (\i -> V2 i i)
fV2IX0 = genVariant (\i -> V2 i 0)
fV2IY0 = genVariant (\i -> V2 0 i)

cSingletonStr :: Functor f => Semioptic f String Char
cSingletonStr = genVariant (\a -> [a])

Invariantについては、genVariantの引数がきちんと同型になるように注意すると性質のよいsemi-opticsが作れます。

iV2ITuple :: Invariant f => Semioptic f (V2 Int) (Int, Int)
iV2ITuple = genVariant (Isomorphism hither yon)
  where
    hither (V2 x y) = (x, y)
    yon (x, y) = (y, x)

iV2Swap :: Invariant f => Semioptic f (V2 a) (V2 a)
iV2Swap = genVariant (Isomorphism f f)
  where
    f (V2 x y) = V2 y x

iCurried :: Invariant f => Semioptic f (a -> b -> c) ((a, b) -> c)
iCurried = genVariant (Isomorphism curry uncurry)
  -- where 
  --   curry f (a, b) = f a b
  --   uncurry f a b = f (a, b)
  -- ↑これらは`base`の関数

-- 商と余り
data QRInt = QRInt {mQuotient :: Int, mRemainder :: Int}

-- 法をデータに付与するコンテナ
-- 0除算を防ぐために、(法-1)の絶対値を非負整数型Wordで表現する
data ModulusWord a = ModulusInt {mSig :: Bool, mMod :: Word, mContent :: a}

word2Int :: Word -> Int
word2Int = fromIntegral

getMod :: Bool -> Word -> Int
getMod True w = word2Int w + 1
getMod False w = negate (word2Int w + 1)

divModMQR :: ModulusWord Int -> ModulusWord QRInt
divModMQR (ModulusWord s m i) = let (q,r) = divMod i (getMod s m) in ModulusWord s m (QRInt q r)

mulAddMQR :: ModulusWord QRInt -> ModulusWord Int
mulAddMQR (ModulusWord s m (QRInt q r)) = ModulusWord s m (q * (getMod s m) + r)

-- ==も所詮Eqという型クラスの演算子なのでオーバーロードできる
instance Eq (ModulusWord Int) where
  ModuluWord _ _ i == ModulusWord _ _ j = i == j

instance Eq (ModulusWord QRInt) where
  mi == mj = mulAddMQR mi == mulAddMQR mj

-- ==が書き換えられたので、同型
iMQR :: Invariant f => Semioptic f (ModulusWord Int) (ModulusWord QRInt)
iMQR = genVariant (Isomorphism divModMQR mulAddMQR)

semi-opticsを消費する際には、具体的なaやsにふれることなくゲッターにしたり更新にしたりすることができる、というのが前章の主張でした。
逆にsemi-opticsを生成するということは、aやsの関係について具体的に記述しながら、最終的にどのような動作になるかが保留された、多態な関数を書くことと等しいです。

合成

さて、semi-opticsの正体は関数の型エイリアスでした。
関数なので、関数合成を考えることができます。

baseには、関数合成演算子(.)があります。乱用すると初心者を振り落とすコードになるのでなるべく封じていましたが、これからほどほどに使います。

(.) :: (b -> c) -> (a -> b) -> (a -> c)
f . g = \a -> f (g a)

合成の向きとしては数学の $f \circ g$ と同じです。

aにf z、bにf y、cにf xを代入してみましょう。

-- sOpticCompose :: (f y -> f x) -> (f z -> f y) -> (f z -> f x)
sOpticCompose :: Semioptic f x y -> Semioptic f y z -> Semioptic f x z
sOpticCompose = (.)

使用例です。

vSwap :: Invariant f => Semioptic f (V2 a) (V2 a)
vSwap = genVariant (Isomorphism swapV swapV) where swapV (V2 x y) = V2 y x

vApp :: (Contravariant f, Semigroup a) => Semioptic f (V2 a) a
vApp = genVariant (Op (\(V2 x y) -> x <> y))

newSO :: (Invariant f, Contravariant f, Semigroup a) => Semioptic f (V2 a) a
newSO = vSwap . vApp

f a -> f sをSemioptic f s aと定義したおかげで、(.)で合成したときにちょっと読みやすくなっています。

前章で、semi-opticsの生成は、aやsの関係について記述されたものを書きながら、消費時の最終形を保留することであると書きました。semi-opticsの合成によって、生成時と同じ保留をしながら、より複雑な関係性を新規に作り出すことができます。

semi-optical carrierとsemi-opticsの同型

Variantness型クラスの定義を再掲します。

class (forall a. k (p a)) => Variantness k p | k -> p, p -> k where
  genVariant :: (k f) => p a s -> Semioptic f s a

kに入る型クラスのことを1-variantnessと呼んでいます、pにも名前をつけたいですね。
運び手という意味でcarrierと呼びましょう。^[25]
semi-opticsのcarrier、semi-optical carrierです。

ちょっと型エイリアスを失礼することでスッキリさせてください。
型クラスkを満たす任意のfに対するSemioptic f s aというのをこう書くことができます。

type ConstrainedSemioptic k s a = forall f. k f => Semioptic f s a

そうすると

genVariant' :: Variantness k p => p a s -> ContrainedSemioptic k s a
genVariant' p = genVariant p

というふうにfを消去した形でgenVariantを書き直すことができます。^[26]

その逆

makeSCarrier :: Variantness k p => ContrainedSemioptic k s a -> p a s

という関数を書くことができれば、carrierとsemi-opticsが同型であるといえそうです。

天下り式にはなるんですが、semi-opticsと同型なcarrierについてこのような型クラスで書くことができます。

class (Variantness k p) => SemiCarrier p k | p -> k, k -> p where
  id' :: p a a

makeSCarrier :: SemiCarrier p k => ContrainedSemioptic k s a -> p a s
-- ↓ 型エイリアスの読み替え
-- makeSCarrier :: SemiCarrier p k => (forall f. k f => Semioptic f s a) -> p a s
-- ↓ Variantnessの定義より、(p a)はkのインスタンスであるためfに代入していい
-- makeSCarrier :: SemiCarrier p k => Semioptic (p a) s a -> p a s
-- ↓ 型エイリアスの読み替え
-- makeSCarrier :: SemiCarrier p k => (p a a -> p a s) -> p a s
makeSCarrier l = l id'

そしてこれまで作ってきた1-variantnessは全部これを満たします。

instance SemiCarrier (<->) Invariant where
  id' = Isomorphism id id

instance SemiCarrier (->) Functor where
  id' = id

instance SemiCarrier Op Contravariant where
  id' = Op id

instance SemiCarrier Daydream Omnivariant where
  id' = Daydream

気分がいいということを感じていただきたいです。この同型性は次章で使います。

ヒエラルキー

1-variantnessの各クラスを見ていると、これらの間になにか包含関係のようなものがある気がしてきます。
具体的には、fがOmnivariantならinstance Functor fもinstance Contravariant fも書けそうですし、fがFunctorかContravariantならinstance Invariant fが書けそうです。書いてみましょう。

-- 各種wrapper
newtype WrappedO f a = WrappedO (f a)
newtype WrappedF f a = WrappedF (f a)
newtype WrappedC f a = WrappedC (f a)

instance (Functor f) => Invariant (WrappedFunctor f) where
  invmap :: (Functor f) => (a -> b) -> (b -> a) -> WrappedF f a -> WrappedF f b
  invmap f _ (WrappedF fa) = WrappedF (fmap f fa) -- (b -> a)を無視する

instance (Contravariant f) => Invariant (WrappedC f) where
  invmap :: (Contravariant f) => (a -> b) -> (b -> a) -> WrappedF f a -> WrappedF f b
  invmap _ g (WrappedC fa) = WrappedC (contramap g fa) -- (a -> b)を無視する

instance (Omnivariant f) => Functor (WrappedO f) where
  fmap _ (WrappedO fa) = WrappedO (omnimap fa) -- (a -> b)を無視する

instance (Omnivariant f) => Contravariant (WrappedO f) where
  contramap _ (WrappedO fa) = WrappedO (omnimap fa) -- (b -> a)を無視する

instance (Omnivariant f) => Invariant (WrappedO f) where
  invmap _ _ (WrappedO fa) = WrappedO (omnimap fa) -- 引数全無視

Wrappedなんちゃらって必要？

instance (Contravariant f) => Invariant f where
  invmap _ g fa = contramap g fa

、と書きたいですね。書きたいんですけど、右辺がHaskellの(というかHaskellのデファクトスタンダードコンパイラGHCの)型推論に差し支える形になってしまうらしく、UndecidableInstances拡張とかいうちょっと癖の悪い魔術が必要になるので、泣く泣くでございます。
型クラスの上下関係というか、クラスベースOOPでいうところの継承みたいな機能はあるにはある^[27]んですが、OmnivariantはともかくとしてFunctor,Contravariant,Invariantは既存の型クラスで、すでに宣言されてしまっているので、親子関係を今更いじることができません。
そのかわりWrappedなんちゃらと、DerivingVia拡張という癖のいい魔術を使うことで

data Daydream a b = Daydream
  deriving (Functor, Contravariant, Invariant) via (WrappedO (Daydream a))

instance Omnivariant (Daydream x) where
  omnimap _ = Daydream

というふうに自動導出させることができるようになります。

このすでに書かれた型クラスに親を再定義することができない、みたいな問題はかつてSemigroupとMonoidの間で起こっていて、Semigroup-Monoid proposalという名前で知られていました。

このへんはちょっとHaskellの弱みではあります。
wrapperとDerivingViaの組み合わせが、結果的に"継承より移譲"っぽい書き心地になることの良し悪しを論ずるのはまたの機会を待ちましょう。

invmapの意味論的には、関数を利用する際には(a -> b)と(b -> a)の両方を耳を揃えて提出しないといけない一方で、呼び出された関数の内部実装としてはどちらかあるいは両方を無視しても構わないという感じになっています。
すなわちなんとかmap(ないしgenVariant)を呼び出すにあたってはOmnivariantよりFunctor/Contravariant、それらよりもInvariantのほうが条件がきつい一方で、各1-variantnessを実装できるfの種類は、Invariantが最も多く、ついでFunctor/Contravariantが多く、Omnivariantが最も少なさそうです。

{(a -> s), (s -> a)}の冪集合とSemi-opticalヒエラルキー

文が長くこみいってきましたね。悪癖です。図の時間かもしれません。

InvariantならばFunctor, InvariantならばContravariant, FunctorならばOmnivariant, ContravariantならばOmnivariantという4つの関係を菱形に書いた図 1-variantness同士の関係

こういう話でした。

一方でこのような図も書けます。

(<->) a sから(->) a sへの関数(Isomorphism f _) -> f), (<->) a sからOp a sへの関数(Isomorphism _ g) -> Op g), (->) a sからDaydream a sへの関数( -> Daydream), Op a sからDaydream a sへの関数( -> Daydream)をVariantnessと同様の菱形に並べた図 semi-optics carrier同士の関係

semi-optics carrierとsemi-opticsの同型関係が思い出されますね。このcarrier同士の関係関数は、Wrappedなんちゃらに対する上位型クラスの実装で引数を捨てていたのと対照できます。

a -> sとs -> aのそれぞれの有無で2*2の4通りの1-variantnessができる、ということについて踏み込んで抽象化すると、冪集合の包含関係による順序が成す束というかっこいい感じの言い方のものが出てきます。出てきますが、要素数が2なので、図としてはこんな感じぽっちです。

要素数2の集合{x, y}の冪集合P({x, y})の要素が成す束 {x,y}の冪集合の包含関係による順序が成す束

うーんシンプル。しかしこれ要素数がちょっと増えると図がほんとうに綺麗になるので、楽しみにしてください。

Semi-opticsなんぞや、そしてそれが有用そうであること、基本的な性質(生成・合成・消費・上下関係)について頭に叩き込んだものとします。^[28]

2階型/2-variantness と Optics

大サビですが、記事が長くて腱がイカれてきたので加速します。
これまでType -> Typeカインドの型fがとりうる型クラスのことである、1-variantnessのことについて考えてきました。
Type -> Type -> Typeカインドの型pがとりうる型クラスのあつまりとして、2-variantnessという名前のものを考えるとしたらこうなりますよね？

class (forall a b. k (c a b)) => Variantness2 k c | k -> c, c -> k where
  genVariant2 :: (k p) => c a b s t -> p a b -> p s t

p a b -> p s tあ～～～～～～～これです。これはOpticsと本当に世間で呼ばれているやつです。久しぶりに僕の造語じゃないやつがでてきました。semi-opticsはこれの半分というつもりで命名したんです。

lensライブラリではちょっと変形したやつがそう呼ばれていますが、相互にトリビアルな変換ができるので問題ありません。

ここでは

type Optic p s t a b = p a b -> p s t

というふうに型エイリアスをつけます。
Variantness2を書き換えます。

class (forall a b. k (c a b)) => Variantness2 k c | k -> c, c -> k where
  genVariant2 :: (k p) => c a b s t -> Optic p s t a b

ここで左辺のcをOptical carrierと呼びましょう。

SemiCarrierにあたるやつも書けます。

class Variantness2 k c => Sell c k | c -> k, k -> c where
  sell :: c a b a b -- 慣用的にsellと呼ばれている

-- type ConstraindOptic k s t a b = forall p. k p => Optic p s t a b
-- makeCarrier :: Sell c k => ContraindOptic k s t a b -> c a b s t
-- ↓ pに(c a b)を代入する
makeCarrier :: Sell c k => Optic (c a b) s t a b -> c a b s t
makeCarrier l = l sell

BifunctorとProfunctor

キーゼルバッハ部位に血が集まってきましたね。クールダウンとして、具体的にVariantness2のインスタンスになる型クラスにどんなものがあるか覗いてみましょう。たとえば、baseからはBifunctorがあります。^[29]

class Bifunctor p where
  bimap :: (a -> s) -> (b -> t) -> p a b -> p s t

instance Bifunctor (,) where
  bimap as bt (a, b) = (as a, bt b)

instance Bifunctor Either where
  bimap as _ (Left a) = Left (as a)
  bimap _ bt (Right b) = Right (bt b)

instance Bifunctor Const where
  bimap as _ (Const a) = Const (as a)

newtype Tagged a b = Tagged {unTagged :: b}

instance Bifunctor Tagged where
  bimap _ bt (Tagged b) = Tagged (bt b)

これって本当にクールダウンなんですか？はい、皆さんやっておられますよ～。
profunctorsライブラリにはProfunctorがあります。^[30]

class Profunctor p where
  dimap :: (s -> a) -> (b -> t) -> p a b -> p s t

instance Profunctor (->) where
  dimap sa bt ab s = bt (ab (sa s))

newtype Forget r a b = Forget {runForget :: a -> r}
instance Profunctor (Forget r) where
  dimap sa _ (Forget ar) = Forget (\s -> ar (sa s))

instance Profunctor Tagged where
  dimap _ bt (Forget b) = Forget (bt b)

余談ですが、昨年のアドベントカレンダーにProfunctorについての記事を書いたことがありました。

Profunctorの一面ではありますが、一面にすぎません。贅沢な使い方です。

Optic carrier

BifunctorとProfunctorについて、carrierの形を考えます。

data Biexchange a b s t = Biexchange (a -> s) (b -> t)

instance Bifunctor (Biexchange x y) where
  bimap as bt (Biexchange xa yb) = Biexchange (\x -> as (xa x)) (\y -> bt (yb y))

instance Variantness2 Bifunctor Biexchange where
  genVariant2 (Biexchange as bt) = bimap as bt

instance Sell Biexchange Bifunctor where
  sell = Biexchange id id

data Proexchange a b s t = Proexchange (s -> a) (b -> t)

instance Profunctor (Proexchange x y) where
  dimap sa bt (Proexchange ax yb) = Proexchange (\s -> ax (sa s)) (\y -> bt (yb y))

instance Variantness2 Profunctor Proexchange where
  genVariant2 (Proexchange sa bt) = dimap sa bt

instance Sell Proexchange Profunctor where
  sell = Proexchange id id

消費

身体がほどよい抽象でポカポカしてきましたね！
では、Optic p s t a bのpに具体的なType -> Type -> Typeを入れて消費してみましょう。

view :: Optic (Forget a) s t a b -> s -> a
view l = runForget (l (Forget id))

review :: Optic Tagged s t a b -> b -> t
review l = unTagged . l . Tagged

coview :: Optic Const s t a b -> a -> s
coview l = getConst . l . Const 

newtype Cotagged r a b = Cotagged {runCotagged :: b -> r}

coreview :: Optic (Cotagged t) s t a b -> t -> b
coreview l = runCotagged (l (Cotagged id))

over :: Optic (->) s t a b -> (a -> b) -> s -> t
over = id

newtype Kiosk c a b = Kiosk {runKiosk :: c -> a -> b}

set :: Optic (Kiosk b) s t a b -> b -> s -> t
set l = runKiosk (l (Kiosk (\b _ -> b)))

preview :: Optic (Forget (Maybe a)) s t a b -> s -> Maybe a
preview l = runForget (l (Forget Just))

coover :: Optic Op s t a b -> (b -> a) -> t -> s
coover l = getOp . l . Op

newtype Star f a b = Star {runStar :: a -> f b}

traverseOf :: Optic (Star f) s t a b -> (a -> f b) -> s -> f t
traverseOf l = runStar . l . Star

newtype Into r p a b = Into {runInto :: p a b -> r}

cooverprod :: Optic (Into r (,)) s t a b -> (a -> b -> r) -> s -> t -> r
cooverprod l = uncurry . runInto . l . Into . curry

cooversum :: Optic (Into r Either) s t a b -> (a -> r) -> (b -> r) -> Either s t -> r
cooversum l ar br = runInto (l (Into (either ar br))) -- either は Data.Eitherの関数

newtype State s a = State {runState :: s -> (a, s)} 

initState :: Optic State s t a b -> a -> State s t
initState l a = l (State (\b -> (a, b)))

-- https://hackage.haskell.org/package/lens-5.3.2/docs/Control-Lens-Traversal.html#v:partsOf の翻案
newtype PartsOf a s t = PartsOf {runPartsOf :: s -> [a] -> ([a], [a], t))}
newtype Proshop a b s t = Proshop {runProshop :: s -> (a, b -> t)}

partsOf :: Optic (PartsOf a) s t a a -> Proshop [a] [a] s t
partsOf l = Proshop (\s -> let f = runPartsOf (l (PartsOf (\(\a as -> let (b, c) = unroll a as in (a:as, b, c))))) s in (let (a, _, _) = f [] in a, \as -> let (_, _, t) = f as in t))
  where 
    unroll a [] = ([], a)
    unroll _ (x: xs) = (xs, x)

余談 Stateモナド

Opticにぶちこんで終わるにはもったいないくらい良いものです。

semi-opticsとは段違いに動きの幅が生まれます。
もはや各方向へのセッターやゲッターがあり、実行前後で型が変換される完全な更新メソッドがあり、その他バラエティ豊かな計算効果があります。多種多様なOptics同士の変換関数すら考えられるようになりました。^[31]

合成

semi-opticsと同様同じpをもつOptic p同士は合成できます。

type Semioptic f s   a   = f a   -> f s
type Optic     p s t a b = p a b -> p s t

型エイリアスSemiopticの定義に際して右辺と左辺でパラメータの配置をひっくり返したのは、関数合成演算子(.)で合成したときに型の数珠つなぎが読みやすくなるためというのもありますが、既存の定義であるOpticに揃えることが目的です。

Opticのほうで何でひっくり返してるかというのはわかりませんが、合成の読みやすさはあるんじゃないかなと思っています。

ともあれ、aとs, bとtという二組の関係を数珠つなぎに複雑に組み上げて、なおかつその関係がどのように消費されるかを保留することができます。

よりみち(Profunctor Optics)

pの条件をProfunctorとその下位クラスに絞ったOpticsは、Profunctor Opticsと呼ばれています。
任意のType -> Type -> Typeの話をしたあとなのできつい制限にみえるかもしれませんが、それだけでひとつのジャンルを築けるくらいの広がりがあります。

これについては、記事が世界に存在しているので、ゆっくりと読みましょう。
さきほどの消費関数のなかでは、view, review, over, set, preview, traverseOf, partsOfがProfunctor Opticsの住人です。

ヒエラルキー

ここで、2-Variantnessを新たにふたつ導入します。

1つめは、Biinvariantです。

class Biinvariant p where
  wmap :: (a -> s) -> (s -> a) -> (b -> t) -> (t -> b) -> Optic p s t a b

data Exchange a b s t = Exchange (a <-> s) (b <-> t)

instance Biinvariant (Exchange x y) where
  wmap as sa bt tb (Exchange (Isomorphism xa ax) (Isomorphism yb by)) =
    Exchange (Isomorphism (as . xa) (ax . sa)) (Isomorphism (bt . yb) (by . tb))

instance Variant2 Biinvariant Exchange where
  genVariant2 (Exchange (Isomorphism as sa) (Isomorphism bt tb)) = wmap as sa bt tb

instance Sell Exchange Biinvariant where
  sell = Exchange id' id'

invariantパッケージではInvariant2という名前になっています。^[32]

2つめは、Absurdityです。

class Absurdity p where
  explode :: Optic p s t a b

data Utopos a b s t = Utopos

instance Absurdity (Utopos x y) where
  explode Utopos = Utopos

instance Variant2 Absurdity Utopos where
  genVariant2 Utopos = explode

instance Sell Utopos Absurdity where
  sell = Utopos

1-variantnessのヒエラルキーの両端にいた両極端InvariantとOmnivariantのように、2-variantのヒエラルキーを書いたときにこのような極端なものが両端に来ると思いませんか？

Biinvariant, Bifunctor, Profunctor, Absurdityのcarrierはどれも、{a -> s, s -> a, b -> t, t -> b}の部分集合である(=冪集合の要素である)とみなせます。
1-variantnessのときには、そのヒエラルキー図が、2要素の……すみません、日本語がかさばるので、記号を入れます。

n要素の集合の冪集合の要素と包含関係からなる束、の記号

説明

n 要素の集合、は 0 から n-1 までの数の集合と同型です。

https://qiita.com/Trubetzkoy/items/ce87d23b46637cf0da00
集合の文脈では、正の整数 n って書いて n 要素の集合を表してもいいということらしいです(？)。[33]
集合 S に対する冪集合は 𝒫(S) や 2^S と書かれます。要素数が本当に 2^{Sの要素数} 個になるのと対応していていいですね。後者で書きます。
束に限らず、なにかあつまりとその間の演算の組で表される構造みたいなのは、コンマ区切りであつまりの名前と演算の名前をならべがちです。

冪集合と包含関係の束は、包含記号 \subseteq を使って (2^S,\subseteq) 、あるいは集合の和と積をつかって (2^S,\cup,\cap) とやったりします。

以降、 $n$ 要素の集合の冪集合の要素と包含関係からなる束について、 $(2^n,\subseteq)$ と書きます。まあ数回書くだけではあるのでコピペしてもいいんですけど、目が滑りますよね。

ヒエラルキー

時を戻しましょう。
1-variantnessのヒエラルキー図は、 $(2^2,\subseteq)$ を使って書けました。
2-variantnessのヒエラルキー図を書くには、 $(2^4,\subseteq)$ を使えば良さそうです。

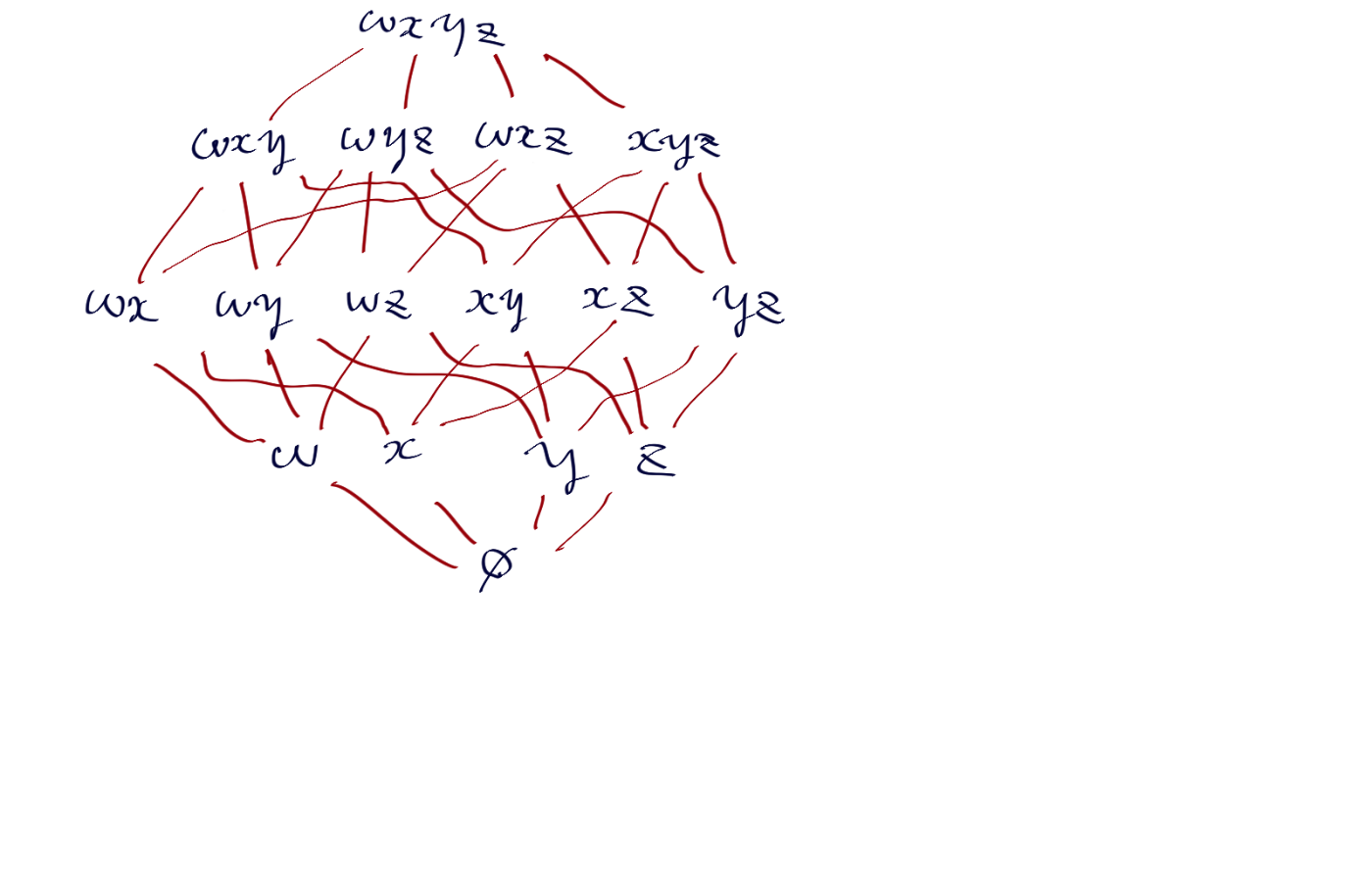
4={w,x,y,z}として、 $(2^4,\subseteq)$

w,x,y,zにa -> s, s -> a, b -> t, t -> bを入れたときBiinvariant, Profunctor, Bifunctor, Absurdityはこの位置に来ます。
(2^4,ubseteq)の中に既知の2-Variantnessを図示 $(2^4,\subseteq)$ 上の2-variantnessの位置

未知なる型クラスが $2^4-4=12$ 個あって、恐ろしいですね。
個人的にこの辺を全網羅するコードを書こうとしたことがあり、実際そこでは16個の型クラスとキャリアを書いて、階層関係を、すべてを概ね16の倍数個書くところまでは終わったのですがあまりに名前に統一感がなかったりその後のところで力尽きていたりで世に出ていません。
ただこの辺を全部やるとさっき"Profunctor Opticsの住人です"と言わなかった物事が整然と並びます。

Biinvariant Opticsとは、私の造語で、この $(2^4,\subseteq)$ にはじまる、BiinvariantとAbsurdityの間にある無数の型クラスのいずれかで制限されたpをもつ、Optic p s t a bのことです。

Profunctor Optics の外にあるものを拾いに行きたかった、というモチベーションから始まりました。Functorチュートリアルから始めて新規概念の話をするのは野蛮だったかもしれませんね。ここまで読んでしまったからには今更です。

私たちは船に乗っています。私は提示しました。私たちがいい感じにします。

展望(strengthの導入、lens/prism)

あとはもう全部余談です。

いままで、aとsの関係、というときに、「a -> sかs -> aもしくはその両方もしくは」と制限していました。他にも関係は考えられます。aのところを(c,a)やEither c aやc -> aと置き換えるみたいな操作をすると、上下関係にあるvariantnessのちょうど間の強さの型クラスが得られます。

variantnessと直交する概念で、個人的にはstrengthと呼ぼうかなと思っています(未定)。

「無数の型クラス」というのはそういうニュアンスもこもっていました。14個って無数というには少ないです。

こういう中間の強さのものを使うと、組み合わせ方によっては、世でLensやPrismやGrateと呼ばれているOpticsが得られます。人々はProfunctor Opticsの話をしているので、それらはProfunctor下のものです。

歴史の話をすると、言葉としてはOpticsよりLens/Prismが先です。
「合成可能なゲッターやセッターの組」として発見/考案されたLensと、その双対Prism。
それらの合成が満たすものとは、そうして得られたものの総称とは……みたいな議論のなかでOpticsという呼び名が与えられたと伝え聞いています。

variantnessの話だけでこんな文字数になってしまいましたし、variantnessとは比べ物にならないくらい組み合わせが爆発するので、現在の型クラスベースアプローチだと人間の脳みそからはみ出してしまいます。
ただ、OpticsがLensやPrismからはじまった概念であるからには、そこへ帰っていかなければなりません。

私たちの宿題とします。海は凪いでいます。

アドベントカレンダー

この記事は仙骨マウスパッド製作委員会アドベントカレンダー2025に参加しています。

https://adventar.org/calendars/11350

脚注

はじめに/ロードマップ

1階型/1-variantness

Functor

V2

mapなんちゃら

型クラス

Functorクラス

Functor以外

Contravariant

Invariant

Omnivariant

1-variantness

semi-optics

利用

生成

合成

semi-optical carrierとsemi-opticsの同型

ヒエラルキー

{(a -> s), (s -> a)}の冪集合とSemi-opticalヒエラルキー

2階型/2-variantness と Optics

BifunctorとProfunctor

Optic carrier

消費

合成

よりみち(Profunctor Optics)

ヒエラルキー

n要素の集合の冪集合の要素と包含関係からなる束、の記号

ヒエラルキー

展望(strengthの導入、lens/prism)

アドベントカレンダー

Discussion