Profunctorってどう使うの？ 〜Lensで学ぶProfunctor〜

はじめに

この記事は、Profunctorという名称や定義などは見たことがあるが、これが何ものなのか、実際どう使うのかワカラン😭という人向けの記事です。

またPureScriptにおいてLensがどのような仕組みで実現されているのかの興味がある人向けでもあります💪

難しそうなところはできるだけ図解を試みました。

どう学ぶ？Profunctor

Profunctorは抽象的であるがゆえの強力さを持っていると思いますが、一方で抽象的であるがゆえ実用のイメージがしづらいかと思います。
このような対象について学ぶ場合のアプローチは色々あるかと思いますが、本記事のアプローチは

「実用されているライブラリでの使い方を見てみよう✨」

です！
実用に足るライブラリの機能がどう実現されているかも知ることができて一石二鳥だ、とモチベーションがわきませんか？（わかない？）

わかないという意見はガン無視🙈して進めます。ちなみに今回はProfunctorが実用されているライブラリとしてタイトル通りLensを取り上げます。
PureScriptにはprofunctor-lensesというライブラリがありますので、こちらのコードを見ながら解説を加えていきます。

PureScriptのLensはHaskellのそれとは大分実装方法が異なるようですが、Profunctorの例としては参考になるかと思います

この記事で登場する方々

解説に入る前に、この記事でご登場願う型クラスやtypeなどを挙げておきます。
漫画とか小説の冒頭の登場人物一覧のようなもので、これらについて解説を行います。

• Profunctorとそのお友達🤝

  • Profunctor
  • Strong

• Lensとゆかいな仲間たち🤝

  • Lens
  • Optic
  • AGetter
  • Setter
  • Fold
  • Forget

ProfunctorやLensにはもっと沢山の関係者がいますが、説明に必要だと考えた最小限の対象に絞っています。

LensにおけるProfunctorの使用例

では、早速ですがLensの使用例と、Lensのライブラリのコードを見てみましょう。

以下はLensを作る例です。Lensを作るにはlens関数を使います。

例

-- テキトーに用意したデータ型
type BoxRec = { value :: String }
data Box = Box BoxRec

_Box :: Lens Box Box BoxRec BoxRec
_Box = lens (\(Box a) -> a) (\_ -> Box)

Lensはgetterとsetterの組だとよく言われていますが、(\(Box a) -> a)がgetterの部分で、(\_ -> Box)がsetterの部分にあたります。

では、lensのコードを見てみましょう。
はい！ドンッ💥

Lens

lens :: forall s t a b. (s -> a) -> (s -> b -> t) -> Lens s t a b
lens get set = lens' (\s -> (Tuple (get s) \b -> set s b))

lens' :: forall s t a b. (s -> Tuple a (b -> t)) -> Lens s t a b
lens' to pab = dimap to (\(Tuple b f) -> f b) (first pab)

profunctor

class Profunctor p where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> p b c -> p a d

上記のコードを図解してみます。

lens関数からはlens'という関数が呼び出されています。
getとsetは、lens'に渡している関数の中で呼び出されています（つまり後から使われます）。
そして、lens'ではdimapという関数を呼び出しています。
これはProfunctorの関数ですね。
ということで出てきましたよ Profunctor。

が、これだけでは「この関数ではProfunctorが使われてるね😄」ということしかわからないでしょう。

私は初見では何もわかりませんでした😨

ということで、解説に移っていきます。

ここではLensを作っただけで使用していません。使用するところはあとでやります。

lensとdimapの話

わかること、わからないこと

さきほどのコードは複雑そうですが、そう見えるのはgetterやsetterなどの関数を使う関数を新しく作って別の関数に渡してたりするからで、冷静に追えばわかる程度のものです。
出てくる型もTupleのような見知った型です。
そこを除くと、よくわからない部分というのはProfunctorとLensの部分になるでしょう。
これらがわかれば動作を理解できそうです。
ということでこれらを説明します👨‍🏫

🏹Profunctor

Profunctorの定義はこうなっています。
型変数pでパラメーター化された型クラスになっていますね。
そしてdimapという関数が定義されています。

profunctor

class Profunctor p where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> p b c -> p a d

このdimapという関数はとても重要な関数で、上記のlens関数の他にもLensのライブラリではしばしば登場します。

それにしても初見ではぱっと見よくわからない関数に見えると思います。
そこでちょっと線を引いてみます。

-> のような意味合いで線を引いてみた
Functionである(->)とこの線をあわせて辿っていくと、aからdまで繋がっています。
そうすると(a -> b)と(c -> d)とp b cを引数として渡すと、aをdに写すp a dのようなものが返ってくるような関数合成のような構造が見えてこないでしょうか。

実際、関数そのものに対するProfunctor型クラスのインスタンスが定義されており、この実装は関数合成そのものです。

型変数pを『関数』にした場合のprofunctorのインスタンス

instance profunctorFn :: Profunctor (->) where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> (b -> c) -> (a -> d)
  dimap a2b c2d b2c = a2b >>> b2c >>> c2d

テストを書いて確認してみます。

dimapのテスト

spec :: Spec Unit
spec = do
  describe "Produnctor Test" do
    it "dimap" do
      let
        fn = dimap show Just ("add " <> _)
      fn 100 `shouldEqual` Just "add 100"

dimapの結果が、show >>> ("add" <> _) >>> Justという合成になることが確認できました。

これはインスタンスが関数の場合の例でしたが、Profunctorは型クラスとして定義されているため、インスタンスによって様々なことを実現できます。例えば、Profunctorを関数(a -> b)と(c -> d)を繋げるような部分と捉えた場合、繋げ方をインスタンスによって変えることで色々やれるわけです。つまり拡張性があります。これは単なる関数合成より抽象的で強力💪です。

さきほど私は「関数合成のような構造が......」と書きましたが、それはここでの説明においては関数合成をイメージすると理解しやすいと考えたからで、構造の捉え方をそのように限定する必要はありません。解釈を限定するよりは、抽象を理解するために具象に行ったあとはまた抽象に戻り、そこからまた具体に、といった具合に抽象と具象を行ったりきたりする方が得られるものは多いと個人的には思います。

しかし私がこのタイミングでPfofunctorは強力🦾と書いてみたところで、あまりそういった実感やイメージが持てない方もおられるのではないかと思います。

やはり具体例が必要だと思います。

ということで、インスタンスの例を一つ紹介しましょう。
どうせならLensで使われている型にします。

🥴Forget

それはForgetです。
見てください。次のようにこの型はProfunctor型クラスのインスタンスになっています。

Forget

newtype Forget :: forall k. Type -> Type -> k -> Type
newtype Forget r a b = Forget (a -> r)

instance profunctorForget :: Profunctor (Forget r) where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> Forget r b c -> Forget r a d
  dimap f _ (Forget z) = Forget (z <<< f)

型変数を見てください。型変数bが右辺にまったく登場しません。
いわゆるPhantom Typeです。

オイオイオイ右辺のヤツ、完全にbを忘れちまってるぞ😮‍💨
すぐわかりますがこれがイイんです。
この型変数としては出てくるけど、使われていないというのがすごくイイ。

ま、それは置いておいてdimapの実装部分も見てみましょう。

Forgetのdimap
(c -> d)の部分が_となっており、まったく使われていません。
定義からForget r b c型の値はForget (b -> r)で、Forget r a d型の値はForget (a -> r)という形になります。
型変数cやdはPhantom Typeなため、出てきません。
Forget zのzは(b -> r)なので、(a -> b)と合成すれば(a -> r)になるので、Forget (z <<< f)はForget (a -> r)にマッチします。

このForgetのdimapの特徴は、2つ目の引数の関数をスルーするというところです。
さきほどイイと書いたのはこういうことができるからなんです。
ちなみにこの特徴がLensで活かされることになります。

Forgetの他にもLensにはProfunctorのインスタンスになっている型が色々ありますので、気になったら調べてみてください。

🔍Lens

次にLensにいきます。
Lensはこのように定義されています。

Lens

type Lens s t a b = forall p. Strong p => Optic p s t a b

type Optic :: (Type -> Type -> Type) -> Type -> Type -> Type -> Type -> Type
type Optic p s t a b = p a b -> p s t

つまりLensとは結局Opticなわけです。わかりやすくするため、Opticを使わないで定義してみます。

Opticを使わない場合の定義

type Lens s t a b    = forall p. Strong p => p a b -> p s t

案外シンプルです。
ここでStrongという新しい型クラスが登場したので、これについても見ていきましょう。

💪Strong

これがStrongの定義です。

Strong

class Profunctor p <= Strong p where
  first :: forall a b c. p a b -> p (Tuple a c) (Tuple b c)
  second :: forall a b c. p b c -> p (Tuple a b) (Tuple a c)

Profunctorがsuperclassになっていますね。
そして何やらfirst``secondという関数はTupleを用いた何かを返すようです。

これまたイメージが浮かびづらいと思うので、具体的なインスタンスをお見せしましょう。

ということで、またForgetにご登場いただきます。
なぜならForgetはStrongのインスタンスでもあるからです💪

Forget

instance strongForget :: Strong (Forget r) where
  first :: forall a b c. Forget r a b -> Forget r (Tuple a c) (Tuple b c)
  first (Forget z) = Forget (z <<< fst) -- Tuple b c は無視されて Tuple a c の a を fst で取って (a -> r) 渡している
  --first (Forget z) = Forget (\(Tuple a _) -> z a) ↑はこういうこと

  second :: forall a b c. Forget r b c -> Forget r (Tuple a b) (Tuple a c)
  second (Forget z) = Forget (z <<< snd)
  --second (Forget z) = Forget (\(Tuple _ a) -> z a) ↑はこういうこと

相変わらず、最後の型パラメーターのことは忘れてしまっています😄

Lens再び

必要な情報が揃ったので、再びlens関数のところに戻ってきました。
(LensのOpticを使わない定義や、ProfunctorやStrongもあわせて載せています)

type Lens s t a b = forall p. Strong p => p a b -> p s t

lens :: forall s t a b. (s -> a) -> (s -> b -> t) -> Lens s t a b
lens get set = lens' (\s -> (Tuple (get s) \b -> set s b))

lens' :: forall s t a b. (s -> Tuple a (b -> t)) -> Lens s t a b
lens' to pab = dimap to (\(Tuple b f) -> f b) (first pab)

class Profunctor p where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> p b c -> p a d

class Profunctor p <= Strong p where
  first :: forall a b c. p a b -> p (Tuple a c) (Tuple b c)

まず、lens'から呼ばれているdimapやfirstはこれまで見てきたように型クラスの関数です。
LensはProfunctor p => p a b -> p s tなので、型変数pがどの型になるかによってdimapやfirstの動作は変わってきますね。

これも何か実際のインスタンスを例にとって見たほうがよいでしょう。

ということで再びForgetの登場です。

pがForget rの場合

まずProfunctorとStrongの（Forgetの）インスタンスの定義をまとめて再掲します。

Profunctor & Strong

instance profunctorForget :: Profunctor (Forget r) where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> Forget r b c -> Forget r a d
  dimap f _ (Forget z) = Forget (z <<< f)

instance strongForget :: Strong (Forget r) where
  first :: forall a b c. Forget r a b -> Forget r (Tuple a c) (Tuple b c)
  first (Forget z) = Forget (z <<< fst)

これをもとにlens'をもう一度見てみましょう。
Lens s t a bとはforall p. Strong p => p a b -> p s tのことであったので、pをForget rにしてみます。

lens'

lens' :: forall r s t a b. (s -> Tuple a (b -> t)) -> Forget r a b -> Forget r s t
lens' to pab = dimap to (\(Tuple b f) -> f b) (first pab)

するとpabの部分は、Forget r a bであることがわかります。

次にForgetのdimapでは(\(Tuple b f) -> f b)は使われないので、返されるのはfirst pabとtoの合成関数を持つForgetとなります。

図解: pがForget rの場合のlens'
firstでTuple a bのaの部分だけ取得しているため、setterであるb -> t(赤枠の部分)は無視されています。
またfirstで取得しているaはgetterの結果でした。
このaがpabであるForget r a bが持っている関数zに渡されています。
つまり、ForgetにおけるLens関数とは、『getterの元ネタsを渡すと、sからgetterで値を取得し、その結果を、渡したForgetが持つ関数に渡した結果を返すという関数を持つForgetを返す』という関数です（文章で書くとわかりづらいな😵‍）。

【lensのgetとsetが、どのタイミングで呼ばれているか】
↑の説明のとおりgetは最初の関数の(s -> Tuple a (b -> t))のaの部分を取得する際に呼び出されます。
またsetは最初の関数(s -> Tuple a (b -> t))の(b -> t)の部分ですが、これは関数なので最初の関数が実行されるときは呼ばれません。
(b -> t)がどこで実行されるか追っていくと。dimapの最後に繋がる関数(\(Tuple b (b -> t)) -> (b -> t) b)で使われていることがわかります（Forgetの場合は無視されますが）。
実装でいうと(\(Tuple b f) -> f b)のf bの部分です。
なのでsetは最後の関数で呼ばれます。

---

さて、ここまででlens関数が返しているLensがなんだか何となくおわかりいただけたのではないでしょうか（特にForgetの場合は）😄
getterとsetterを使う大枠の部分と、関数を繋げる部分を切り離しておき、その繋げる部分をProfunctorのインスタンスによって差し替えられるようになっているわけです。
ちなみにLensの他の仲間たち、例えば代数的データ型のような直和型を扱うPrismや、配列的な値を扱えるAffineTraversalなどでもdimapが使われていますが、同じような考え方で作られていると思います。

Lensを使う

ここまでは、Lensを作るところまでを解説してきましたので、次は実際に作ったLensを使った場合の動作について見ていきたいと思います🙋‍♂‍

例として値の取得と設定を行うテストを書いてみました。

Box

type BoxRec = { value :: String }
data Box = Box BoxRec

-- テストで使うためのShowとEq
instance showBox :: Show Box where
  show (Box b) = _.value b
instance eqBox :: Eq Box where
  eq (Box b1) (Box b2) = _.value b1 == _.value b2

-- BoxのLensを定義
_Box :: Lens' Box BoxRec
_Box = lens (\(Box a) -> a) (\_ -> Box)

テスト

spec :: Spec Unit
spec = do
  describe "Lensのテスト" do
    it "viewで値を取得することができる" do
      let
        box = view _Box (Box {value: "Value"})
      box `shouldEqual` {value: "Value"}

    it "setで値を設定することができる" do
      let
        box = set _Box {value: "NewValue"} (Box {value: "Value"})
      box `shouldEqual` Box {value: "NewValue"}

👓view

Lensを使って値を取得するために使えるのがview関数です。
定義を見てみましょう。

view

view :: forall s t a b. AGetter s t a b -> s -> a
view l = unwrap (l (Forget identity))

新しいおともだちAgetterが登場したので、viewの内容を見る前にAGetterの定義を見てみましょう。

AGetter

type AGetter :: Type -> Type -> Type -> Type -> Type
type AGetter s t a b = Fold a s t a b

type Fold :: Type -> Type -> Type -> Type -> Type -> Type
type Fold r s t a b = Optic (Forget r) s t a b

type AGetter s t a b = Forget a a b -> Forget a s t

結局AGetterはtype Foldなのですが、Foldを見ると見慣れたOpticとForgetを使って定義されています。
わかりやすくするため、FoldやOpticを使わないで定義してみるとこうなります。

FoldやOpticを使わないで定義した版

type AGetter s t a b = Forget a a b -> Forget a s t

なんとAGetterとはこれまで散々見てきたForgetでした。
Forget a a b = Forget (a -> a)で、Forget a s t = Forget (s -> a)です。

AGetterの定義がわかったところで、viewの定義に戻ります。

view

view :: forall s t a b. AGetter s t a b -> s -> a
view l = unwrap (l (Forget identity))

これをForgetで置き換えてみるとこうなります。

view

view :: forall s t a b. (Forget a a b -> Forget a s t) -> s -> a
view l = unwrap (l (Forget identity))

lは(Forget a a b -> Forget a s t)という関数なので、引数を(Forget identity)として呼び出すことができます（Forget a a b = Forget (a -> a)だから）。
するとForget a s t型の値が返ってきます。Forget a s t = Forget (s -> a)なので、これをunwrapすると(s -> a)。この関数を引数sで呼び出すとaが返ってくる、というわけです。

ところでこの(Forget identity)はどう使われているのでしょうか？
まず、そもそも上記の例ではview関数の引数として、Lens型の値を渡していました。
あらためてLensの定義を見てみます(Opticを使わない形に書き換えてあります)。

Lens

type Lens s t a b = forall p. Strong p => p a b -> p s t

そしてAGetterの定義と見比べてみましょう(こちらもOpticを使わない形に書き換えてあります)。

AGetter

type AGetter s t a b = Forget a a b -> Forget a s t

ここで、Forgetが型クラスStrongのインスタンスであったことを思い出してください。
故にAGetterを引数にとる関数にLens型の値を渡した場合、Forgetのインスタンスが選択されることになります。

ところでlens関数の型変数pがForgetだった場合の説明は、既にしていましたね？
もう一度、図を見てみましょう。
今回はpabであるForgetが持っている関数がidentityだということがわかっているので、そのように図を更新してあります。またForgetの場合setterは使われないので図では着目していません。

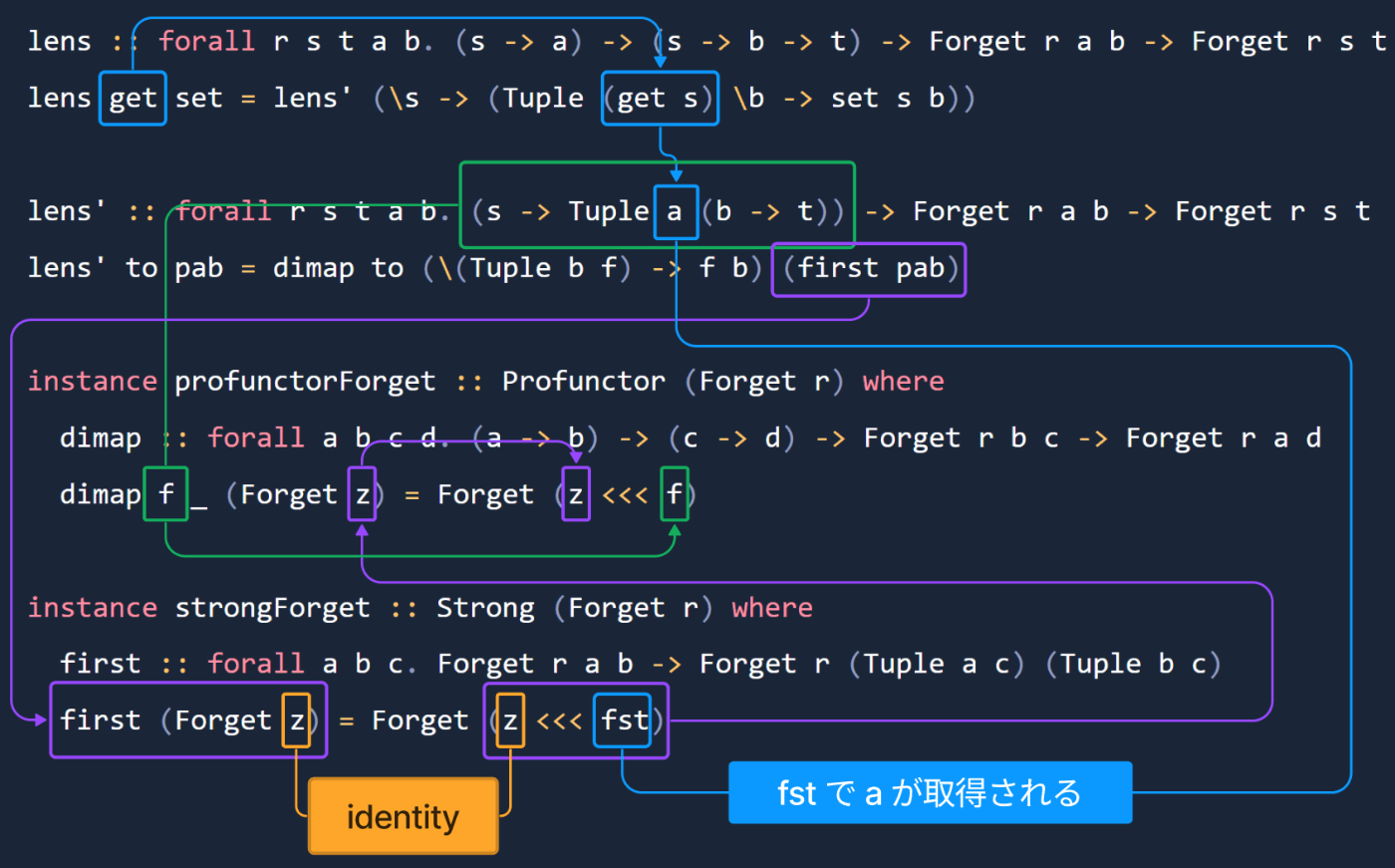
つまり、view関数は、getterで取得した値をそのまんま返しているというわけです。

🤏set

次にset関数です。
定義はこうです。

set

set :: forall s t a b. Setter s t a b -> b -> s -> t
set l b s = over l (const b) s

over :: forall s t a b. Setter s t a b -> (a -> b) -> s -> t
over l = l

また新しいお友達Setterが出てきたのでこちらの定義も見ましょう。

Setter

type Setter s t a b = Optic Function s t a b

お馴染みのOpticを使わない定義も見てみます。
Optic pの部分を見てみると、単なる関数になっています。

Opticを使わない定義

type Setter s t a b  = (a -> b) -> (s -> t)

ではSetterの定義を見たところで、setのコードを見てみましょう。

set

set :: forall s t a b. Setter s t a b -> b -> s -> t
set l b s = over l (const b) s

overから返される関数(a -> b) -> s -> tに、引数として(const b)とsを渡しています。
つまりa -> bにconst bが、sにはまんまsが渡されて、tが返ってきます。
const bなのでaがどのような値であろうとbはそのまま渡されます。
overも見てみましょう。
SetterをOpticを使わない形で置き換えてみると、overの型アノテーションはこうなります。

((a -> b) -> (s -> t)) -> (a -> b) -> s -> t

((a -> b) -> (s -> t))型の関数に、引数として(a -> b)型の関数を渡すと、(s -> t)型の関数が返され、その関数に引数としてsを渡してtが返るというわけですね。

さて、setに渡されているlとは、Lens型の値でした（viewのときと同じく）。

ということで、またまたLensとlens関数を見てみます。

Lensとlens

type Lens s t a b = forall p. Strong p => p a b -> p s t

lens :: forall s t a b. (s -> a) -> (s -> b -> t) -> Lens s t a b
lens get set = lens' (\s -> (Tuple (get s) \b -> set s b))

lens' :: forall s t a b. (s -> Tuple a (b -> t)) -> Lens s t a b
lens' to pab = dimap to (\(Tuple b f) -> f b) (first pab)

class Profunctor p where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> p b c -> p a d

class Profunctor p <= Strong p where
  first :: forall a b c. p a b -> p (Tuple a c) (Tuple b c)

setの場合、Strong pのpが何になるかというと、Optic FunctionとなっていたことからわかるようにFunctionすなわち->になります。
一番最初の方で書いたのですが、次のように->もまたProfunctorのインスタンスになっているため、可能なのです。

型変数pを『関数』にした場合のprofunctorのインスタンス

instance profunctorFn :: Profunctor (->) where
  dimap :: forall a b c d. (a -> b) -> (c -> d) -> (b -> c) -> (a -> d)
  dimap a2b c2d b2c = a2b >>> b2c >>> c2d

これは単なる関数合成ですね🙂
Strongの方はこうです(Strongにはsecondという関数も定義されているのですが省略しています)。

Strong (->) のインスタンス

instance strongFn :: Strong (->) where
　first :: forall a b c. (a -> b) -> (Tuple a c) -> (Tuple b c)
  first a2b (Tuple a c) = Tuple (a2b a) c

これでdimapとfirstの実装がわかったので、lensの動きもわかりそうです。
図解してみましょう。

set関数はLensの関数であるlに、引数pabとしてconst bを渡していました。

set :: forall s t a b. Setter s t a b -> b -> s -> t
set l b s = over l (const b) s

これはfirstにおけるa2bの部分にあたります。またconst x yとは、yの値がなんであれ必ずxを返すという関数なのでconst bは常にbを返す(a -> b)型の関数となります。
このbはset関数の引数として渡した値で、setしたい値そのものになります。
そしてこの関数const bに渡されるaとはLensのgetterの結果です。
なのでgetterで取得した値は無視されるということになります（図の青枠の部分）。
setの場合のdimapは単なる関数合成なのですが、処理を見てみるとsetterはviewのときと異なり最後の関数まで渡ってきています（赤枠の部分）。そしてb -> set s bの結果最終的にset s bの結果であるtが返ります。

---

viewとsetどちらも同じlens関数で生成されたLensを使っていますが、viewのときはsetterが無視され、setのときはgetterが無視されるということが実現できていることがわかったかと思います🧙
そしてそれを実現しているのがProfunctorなのでした。

おわりに

今回の記事では、Lensという有名なライブラリの実装を通じて、実用的なProfunctorの使われ方を見てきました。
抽象的ゆえに様々な使い方が考えられると思いますが、一例として、抽象化されている部分を『対象と対象を繋ぐ部分』と捉えることで、オープン・クローズドの原則を満たす形で拡張性を持たせるという使い方があることがご理解いただけたかと思います。
Lensのライブラリには、他にもPrismにおけるChoiceの実例であったり、AffineTraversalでの更なるStrongの実例だったりがあり、Profunctor関連の実例の宝庫💎なので、もし興味がわきましたらぜひ参考にしていただきたいと思います。

おまけ (Lensの合成)

おまけとしてLensを合成した場合、どうなっているのか軽く説明してみます。

まずLensを2つ作ってみます。

-- テキトーな入れ物
type BoxRec = { value :: String }
data Box = Box BoxRec

-- Boxを持ってるだけ
newtype Container = Container Box

instance showBox :: Show Box where
  show (Box b) = _.value b
instance eqBox :: Eq Box where
  eq (Box b1) (Box b2) = _.value b1 == _.value b2

derive newtype instance showContainer :: Show Container
derive newtype instance eqContainer :: Eq Container

-- Lens
_Box :: Lens' Box BoxRec
_Box = lens (\(Box a) -> a) (\_ -> Box)

-- Lens
_Container :: Lens' Container Box
_Container = lens (\(Container b) -> b) (\_ -> Container)

このLensを合成したものを使ってview関数を呼び出してみると、普通に値を取得できます（当たり前）

test

spec :: Spec Unit
spec = do
  describe "Getter Test" do   
    it "view" do
      let
        box = view (_Container <<< _Box) (Container $ Box {value: "Value"})
      box `shouldEqual` {value: "Value"}

なぜ(_Container <<< _Box)のようにLensを合成することができるのでしょうか🤔？

ご存知の通りLens s t a bとはforall p. Strong p => p a b -> p s tのことでした。
上記の定義をこちらの定義で書き換えてみるとわかりやすいのでやってみます。

_Box' :: forall p. Strong p => p BoxRec BoxRec -> p Box Box
_Box' = _Box

_Container' :: forall p. Strong p => p Box Box -> p Container Container
_Container' = _Container

この定義であれば次のように合成できることが容易にわかるかと思います。

composed1 :: forall p. Strong p => p BoxRec BoxRec -> p Container Container
composed1 = _Container <<< _Box

今度は上記の定義をLensを使った定義に戻してみます。

composed2 :: Lens' Container BoxRec
composed2 = _Container <<< _Box

Lensの合成はこのようになっています。

最後にview関数を使う場合どうなるかを見てみましょう。

view関数の引数はAGetterで、これは定義的にはForgetを用いた関数なのでインスタンスとしてはForgetのインスタンスが選択されます。
ということで上記をForgetにしてみます。

composed3 :: Forget BoxRec BoxRec BoxRec -> Forget BoxRec Container Container
composed3 = _Container <<< _Box

---

以上で、おまけは終りになります🔚