LFUの進化形! キャッシュ置換アルゴリズムW-TinyLFUを図解する
はじめに
前回の記事ではLRUベースのキャッシュ置換アルゴリズムであるSLRU、ARC、LIRSについて解説しました。
この記事ではLFUを改良したキャッシュ置換アルゴリズムであるW-TinyLFUについて解説します。
LFUの課題
LFU(Least Frequency Used)は、最も高頻度でアクセスされるデータエントリーをキャッシュに残していく戦略です。
LFUはデータエントリーへのアクセス頻度が時間的に一定である場合にキャッシュヒット率が高くなるキャッシュ置換アルゴリズムです。
しかし、LFUには二つの問題が存在します。
第一に、LFUは各データエントリーのアクセス頻度を管理するために複雑で大量のメタデータを保持する必要があります。
第二に、ほとんどの実世界のシナリオでは、アクセス頻度は時間とともに急激に変化します。 例えば動画視聴サービスにおいて、ある日突然大人気となった動画が数日後には全くアクセスされなくなるといったケースは一般的です。このように一度高い頻度でアクセスされたからといって、データ・アイテムをキャッシュに保持し続けることは必ずしも最適とは言えません。
こうした欠点を改善するために、多くのLFUを代替するアルゴリズムが考案されています。今回解説するW-TinyLFUもその一つです。
TinyLFU
W-TinyLFUを解説する前にその前身であるTinyLFUについて解説します。
概要
TinyLFUのアーキテクチャは下図の通りです。
図が示すようにTinyLFUは基本的に単体では使用されず、他のキャッシュ置換アルゴリズムを補助する役割で使用されます。
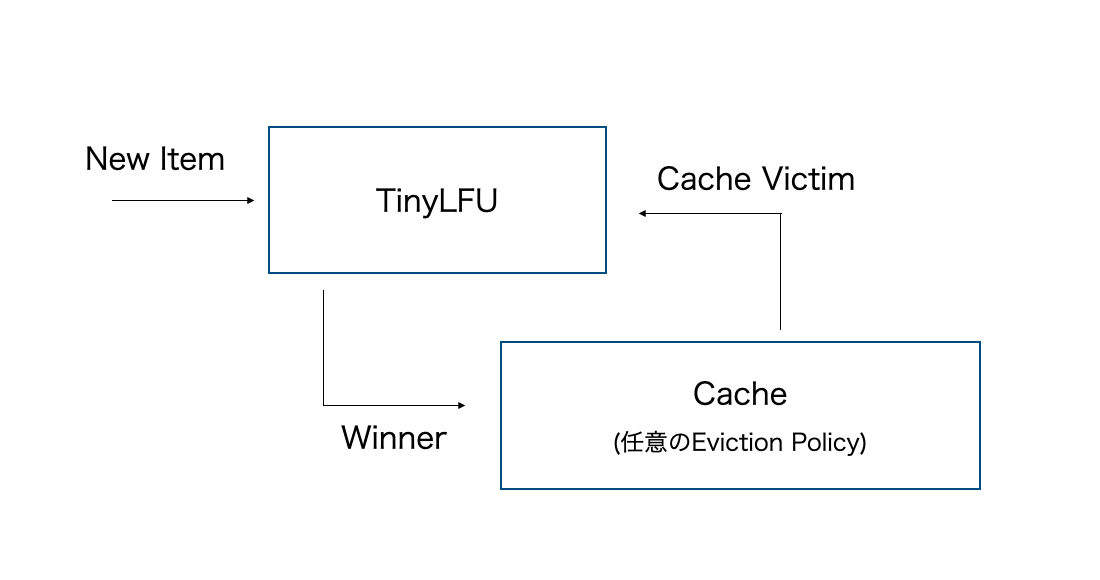
新しいデータが挿入される際にキャッシュ領域がいっぱいである場合、キャッシュ置換アルゴリズムは消去するデータエントリーの候補をTinyLFUに提示します。
そして、TinyLFUはその消去候補を新しいデータエントリーで置き換えることがキャッシュヒット率の向上に寄与するかを判断します。
置き換えるのが良いと判断すれば、新しいデータエントリーをキャッシュに取り込みます。
逆に消去候補を残した方がいいと判断すれば、新しいデータエントリーを破棄し、消去候補をキャッシュに戻します。
TinyLFUの統計情報
TinyLFUはLFUと同様に過去のキャッシュアクセスに関する統計情報をもとにキャッシュエントリの置換を判断します。
長期間にわたってデータ・アイテムのアクセス頻度に関する統計情報を維持する必要がありますが、このような長期間のアクセス履歴を正確に保持することは現実的ではありません。
そのため、TinyLFUはCounting Bloom Filterと呼ばれる確率的データ構造による近似的な統計情報を保持しています。
Counting Bloom Filterについて解説する前に、まずはその基礎となるBloom Filterから解説していきます。
Bloom Filter
Bloom Filterは要素が集合のメンバーであるかどうかをテストできる空間効率の良い確率的データ構造です。
偽陽性(要素が集合内に含まれていないのに含まれていると判定する)の可能性はありますが、偽陰性(集合内に含まれている要素を含まれていないと判定する)になることはないのが特徴です。
集合へのデータの追加
Bloom FilterはmビットのBoolean配列として表現されます。
データを追加する際にはk個のハッシュ関数を適用して、配列インデックスを取得します。そして、そのインデックスに対応する配列の位置のビットを立てます(0→1)。
要素が集合内にあることの判定
ある要素がその集合に含まれるかどうかを調べるには、それをk個のハッシュ関数に入力してk個の配列インデックスを取得します。
それらの位置にあるビット群のどれかひとつでも0である場合は、その要素はその集合には含まれていないと判定できます。
逆にそれらの位置にある全てのビットが1であれば、その要素はその集合に含まれているか、またはそれらのビットは他の要素を追加したときにたまたま全部1になった(偽陽性)ものであると考えられます。

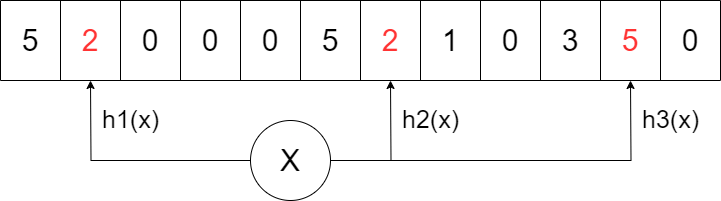
集合 {x, y, z} を表現したブルームフィルタ(m=18、k=3)の例。色つきの矢印は各元に対応しているビット配列上のインデックスを示している。元wは集合 {x, y, z} に含まれないので、対応するビット位置の一部がゼロになっている。
参考 ブルームフィルタ
Counting Bloom Filter
従来のBloom Filterでは「集合内の要素を削除する」操作が不可能でした。
しかし、キャッシュ置換アルゴリズムはキャッシュ内に存在する要素を削除して別の要素に置き換えるのが責務です。そのため削除操作ができないという特徴はキャッシュ置換アルゴリズムで使用する上で非常に不便です。
Counting Bloom FilterではBloom Filterにおける配列の要素を単一ビットからnビットのカウンタに拡張しています。
これによりBloom Filterでは難しかった「集合内の要素を削除する」操作を実現しています。
データの追加と削除
集合にデータを追加する際は、通常のBloom Filterと同様に当該データに対して各種ハッシュ関数を適用し、配列インデックスを取得します。
ここで通常のBloom Filterでは対応する配列要素を0→1にしますが、Couting Bloom Filterではその代わりに対応するインデックスのカウンタをインクリメントします。
逆に削除する場合は対応する配列要素のカウンタをデクリメントします。
Freshness Mechanism
元々のLFUでは要素のアクセス頻度をリセットする方法がないので、急なアクセスパターンの変化に対応できないのが欠点でした。
TinyLFUのCouting Bloom Filterにおいては最新のデータアクセスパターンを反映するためにFreshness Mechanismによって統計情報のクリーンアップが実行されます。
具体的にはグローバル・カウンタSを定義します。
このSをアイテムの追加の度にインクリメントしていき、Sの値がサンプルサイズWに達すると、すべてのカウンタを2で割って、S=W/2に更新します。
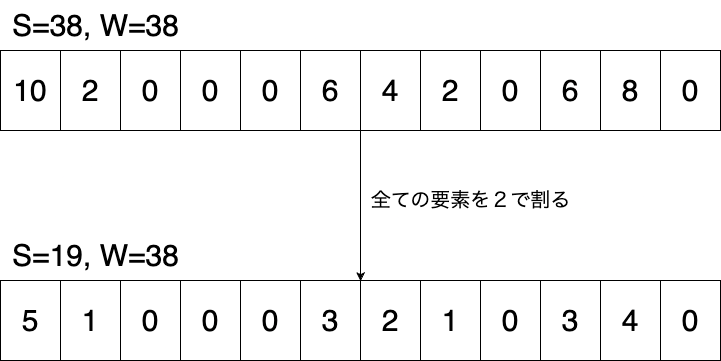
この操作により過去にアクセス頻度が高かったが、現在はアクセスされなくなったデータのカウンタを削減することができ、現在のアクセスパターンをより統計情報に反映することができます。
Couting Bloom Filterの空間容量の最適化
従来のCounting Bloom Filterではアクセス頻度の高い要素も低い要素もともにnビットのカウンタが割り当てられていました。
しかし、アクセス頻度の低い要素はカウンタ値が小さいため、これらにnビットの空間を割り当てるのは無駄です。
こうしたアクセス頻度の低い要素に対して割り当てるカウンタのサイズを減らすためにDoorkeeperと言う手法が提案されました。
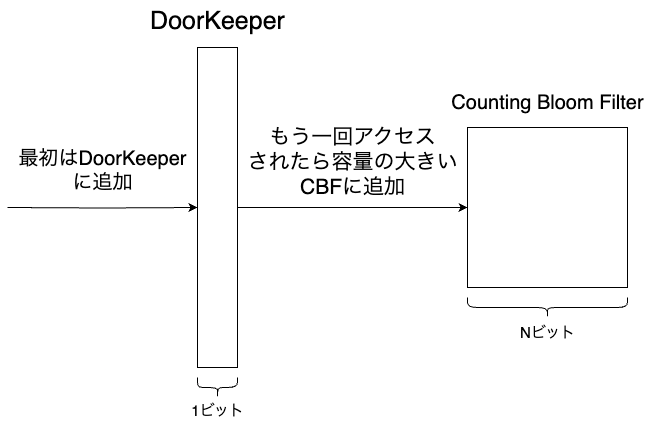
DoorkeeperとはCounting Bloom Filterの前段に配置された通常のBloom Filterのことです。
新しい要素が挿入されたとき、その要素がすでにDoorKeeperに存在すれば、Counting Bloom Filterに挿入されます。
その要素がDoorKeeperに存在しない場合は、DoorKeeperへ挿入されます。
このようにすることで一度しかアクセスされない要素はDoorKeeperにだけ挿入されるので、そうした要素に割り当てるカウンタのサイズを1bitに制限することができます。
また、DoorKeeperは前述したFreshness Mechanismが実行された際にリセットされます。
これによりキャッシュする意義の低い一度しかアクセスされない要素をキャッシュからクリアすることが可能になります。
W-TinyLFU
概要
TinyLFUではLFUの課題に対する一定の解決策を提供しました。
具体的にはCounting Bloom Filterによりアクセス頻度の統計情報の空間容量を削減し、Freshness Mechanismによりアクセスパターンの変化に対応することができるようになりました。
しかしながら、TinyLFUにはバーストアクセス時に特定の要素のカウンタ値が極端に高くなり、バーストアクセス終了後もそのデータがCounting Bloom Filterから長い間排除されない可能性があるという欠点が残っています。
これにより、TinyLFUは一般的なワークロードにおいてLRUよりも性能が悪いことが知られています。
その一方でLRUは単純に最近アクセスされていない要素をキャッシュから排除するため、上記の欠点はLRUには存在しません。
そのため、LRUとTinyLFUを組み合わせてバーストアクセスへの耐性を強化したW-TinyLFUというアルゴリズムが考案されました。
構成
W-TinyLFUは、以下のようにキャッシュをWindowキャッシュとメインキャッシュの2つに分割します。

メインキャッシュの前段にはTinyLFUが配置されます。
W-TinyLFUを構成するTinyLFUでは前述したCounting Bloom Filterの代わりにCount-Min Sketchというデータ構造を使用しています。
Windowキャッシュはキャッシュ置換アルゴリズムとしてLRUを使用し、メインキャッシュはSLRUを使用しています。(SLRUについての詳細は前回の記事を参照してください。)
アイテム追加時の挙動
キャッシュミスが発生するたびに、アクセスされたアイテムはWindowキャッシュに挿入されます。
Windowキャッシュがいっぱいになると、LRUに従ってデータ項目が消去され、消去されたデータ項目については、TinyLFU (Count-Min Sketch)に従ってメイン・キャッシュに入るかどうかが決定されます。
Count-Min Sketch
前節のTinyLFUではCounting Bloom Filterという確率的データ構造を用いて要素の存在判定を行なっていました。
W-TinyLFUではこれをさらに発展させたCount-Min Skecthというデータ構造を用いて、単に存在判定をするだけでなく当該要素の参照頻度を確率的に算出しています。
これにより、Windowキャッシュの削除対象とMainキャッシュの削除対象の参照頻度を比較して、より参照頻度の高い方をキャッシュ中に残すという選択ができるようになっています。
Counting Bloom Filterとの違い
Count-Min Sketchは大まかなコンセプトはCounting Bloom Filterと似ていますが、以下のようにハッシュ関数の分だけ配列を用意するという点が異なっています。
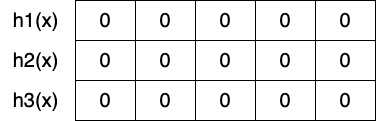
要素の追加時は以下のようにそれぞれのハッシュ関数の出力値をオフセットとして、そのハッシュ関数に対応する配列の要素をインクリメントします。

参照頻度の推定値算出
ある要素の参照頻度を推定するには、当該要素に対して各ハッシュ関数を適用して配列要素にマッピングします。それらの最小値が参照頻度の推定値となります。
ただし、ハッシュ値が衝突することでこの推定値が実際の参照頻度よりも多くなる可能性があります。
Count-Min Sketchの疑似コード
class CountMinSketch:
def __init__(self, width: int, k_num: int):
self.width = width
self.k_num = k_num
self.counters = [[0 for _ in range(self.width)] for _ in range(self.k_num)] # counterとしてk_num個の配列を用意する
self.mask = (1 << (self.width - 1).bit_length()) - 1
# keyに対してk_num個のハッシュ関数を適用して配列オフセットを取得する
# そのオフセットに対応する要素集合の最小値に等しい要素をインクリメントする
def increment(self, key: Hashable):
hashes = [hash(key, k_i) for k_i in range(self.k_num)]
lowest = min(self.counters[k_i][hashes[k_i]] for k_i in range(self.k_num))
for k_i in range(self.k_num):
if self.counters[k_i][hashes[k_i]] == lowest:
self.counters[k_i][hashes[k_i]] += 1
# keyに対応するcounterを取得し、その最小値を推定頻度として返す
def estimate(self, key: Hashable) -> int:
hashes = [self.hash(key, k_i) for k_i in range(self.k_num)]
return min(self.counters[k_i][hashes[k_i]] for k_i in range(self.k_num))
# すべての配列要素を0にクリア
def clear(self):
self.counters = [[0 for _ in range(self.width)] for _ in range(self.k_num)]
# freshness mechanism
def reset(self):
self.counters = [[counter // 2 for counter in counters] for counters in self.counters]
W-TinyLFUの疑似コード
最後に上記のCount-Min Sketchコードを使用したW-TinyLFUの疑似コードを以下に提示します。
class WTinyLfuCache:
def __init__(self, cap, sample_size):
window_cache_cap = max(1, int(cap * 0.01))
main_cache_cap = max(1, cap - window_cache_cap)
self.approximation_sketch = CountMinSketch(sample_size)
self.sample_size = sample_size
self.S = 0 # Freshness MechanismのグローバルカウンタS
self.doorkeeper = BloomFilter(sample_size, 0.01)
self.window_cache = LruCache(window_cache_cap)
self.main_cache = LruCache(main_cache_cap)
# キャッシュに要素を追加する
def push(self, key, val):
# すでにWindowキャッシュに含まれているなら、その先頭に移動させる
if key in self.window_cache:
return self.window_cache.push(key, val)
# すでにMainキャッシュに含まれているなら、その先頭に移動させる
if key in self.main_cache:
return self.main_cache.push(key, val)
window_cache_victim = self.window_cache.push(key, val)
# Windowキャッシュがいっぱいの場合
if window_cache_victim is not None:
window_cache_victim_key, window_cache_victim_val = window_cache_victim
# Mainキャッシュがいっぱいの場合
main_cache_victim = self.main_cache.peek_lru_if_full()
if main_cache_victim is not None:
main_cache_victim_key, _ = main_cache_victim
window_cache_victim_estimation = self.estimate(window_cache_victim_key)
main_cache_victim_estimation = self.estimate(main_cache_victim_key)
# Windowキャッシュの削除候補とMainキャッシュの削除候補の参照頻度を比較して、勝った方をMainキャッシュに残す
if window_cache_victim_estimation > main_cache_victim_estimation:
return self.main_cache.push(window_cache_victim_key, window_cache_victim_val)
return window_cache_victim
# MainキャッシュがいっぱいでなければWindowキャッシュの削除候補をMainキャッシュに追加
return self.main_cache.push(window_cache_victim_key, window_cache_victim_val)
return None
# キャッシュ中の要素を取得
def get(self, key):
val = None
if key in self.window_cache:
val = self.window_cache.get(key)
elif key in self.main_cache:
val = self.main_cache.get(key)
if val is not None:
if self.doorkeeper.check(key):
# Count-Min Sketchのkeyに対応する部分をインクリメント
self.approximation_sketch.increment(key)
self.S += 1
# グローバルカウンタSがサンプルサイズを超えたらFreshness Mechanismを実行する
if self.S >= self.sample_size:
self.approximation_sketch.reset()
self.doorkeeper.clear()
self.S = 0
else:
self.doorkeeper.set(key)
return val
# Count-Min Sketchでkeyに対応する要素の参照頻度推定値を取得
def estimate(self, key):
estimate = self.approximation_sketch.estimate(key)
# keyがdoorkeeperにあれば、doorkeeper分の参照回数(1回)を推定値に追加する
if self.doorkeeper.check(key):
estimate += 1
return estimate
まとめ
この記事では、LFU(Least Frequently Used)を改良したキャッシュ置換アルゴリズムであるW-TinyLFUについて詳しく解説しました。
W-TinyLFUでは、LFUの統計情報のサイズが大きいという欠点をCount-Min Sketchにより解消していることが理解できたと思います。
次回はキャッシュ置換アルゴリズムのCLOCK、SIEVEについて解説する予定です。
参考
Discussion