図解キャッシュ置換アルゴリズム(SLRU, ARC, LIRS)
はじめに
前回の記事ではLRUとLFUについて解説しました。
この記事ではLRUの欠点を改良したアルゴリズムであるSLRU、ARC、LIRSアルゴリズムについて解説します。
SLRU
SLRUの概要
LRUには、一度しかアクセスされないようなエントリーが、他の頻繁にアクセスされるエントリーをキャッシュから削除してしまう場合があるという欠点があります。
このため、キャッシュ領域が十分に長くない場合、疎なアクセスパターンによって多数のエントリーがキャッシュから削除され、アクセス頻度の低いエントリーがキャッシュに大量に残り、キャッシュ・ヒット率が低下するという事態(キャッシュ汚染)が発生する可能性があります。
SLRU(Segmented LRU)はLRUを改良したものでキャッシュに入ってから2回以上ヒットしたエントリーとまだ1回しかヒットしていないエントリーを分けて管理することで短期的にアクセス頻度の高い要素を保護することのできるアルゴリズムです。
SLRUの管理構造
SLRUでは以下のように一定の割合(下の例では8:2とした)でLRUキャッシュをProtectedセグメントとProbationセグメントという2つのセグメントに分割します。
この分割の割合はパラメータとして設定が可能です。

2回以上ヒットしたエントリーはProtectedセグメントへ、1回しかヒットしていないエントリーはProbationセグメントへ格納されます。
新規エントリーの追加
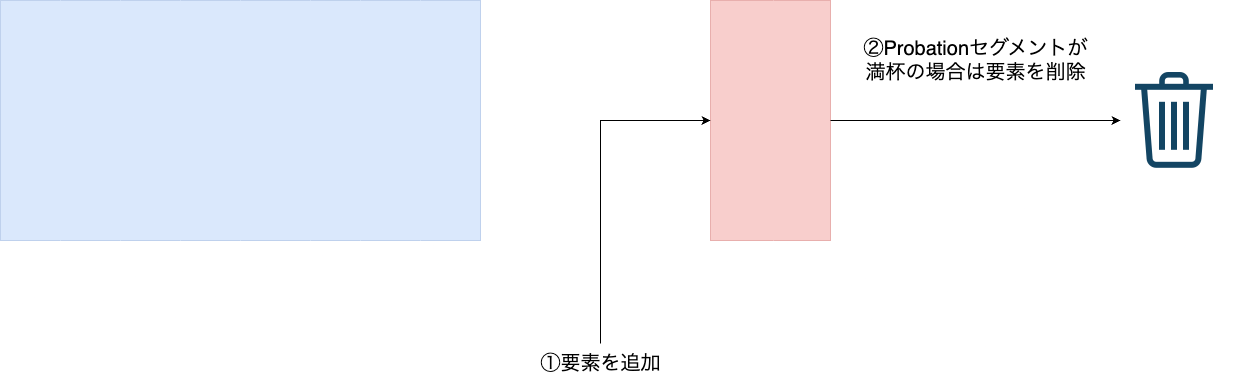
初めてアクセスされたエントリーはProbationセグメントに入ります。
この際にProbationセグメントがいっぱいの場合はエントリーが一つ削除されます。
この削除されたProbationセグメントのエントリーは、保護されずキャッシュから完全に削除されます。
キャッシュアクセス時の挙動
1. Probationセグメント内のエントリーへのアクセス
Probationセグメント内のエントリーで再度アクセスされたものはProtectedセグメントに入ります。

Protectedセグメントがいっぱいの状態でエントリーが追加された場合はProtectedセグメントからエントリーが削除されます。
削除されたProtectedセグメントのエントリーは、Probationセグメントへ移動します。
2. Protectedセグメント内のエントリーへのアクセス
Protectedセグメント内のエントリーがアクセスされた場合は当該エントリーがProtectedセグメントのLRUの先頭へ移動します。

SLRUの疑似コード
from collections import deque
class SLRUCache:
def __init__(self, cap):
self.cache = {}
self.protectedCap = int(cap * protectedRatio)
self.probationCap = cap - self.protectedCap
self.probationLs = deque()
self.protectedLs = deque()
def length(self):
return len(self.probationLs) + len(self.protectedLs)
def write(self, entry):
# すでにcacheにentryが存在する場合
if entry in self.cache:
self.markAccess(entry)
return
# キャッシュ内にentryが存在しない場合、probationセグメントに当該entryを追加
entry.listID = 'probationSegment'
self.probationLs.appendleft(entry)
self.cache[entry] = entry
# entryの追加によりprobationセグメントがいっぱいになったら一番古いエントリーを削除
if self.probationCap > 0 and len(self.probationLs) > self.probationCap:
entry = self.probationLs.pop()
return self.remove(entry)
return
def access(self, entry):
if entry in self.cache:
self.markAccess(entry)
def markAccess(self, entry):
# protectedセグメント内のentryにアクセスした場合、当該entryをprotectedセグメントの先頭に移動する
if entry.listID == 'protectedSegment':
self.protectedLs.remove(entry)
self.protectedLs.appendleft(entry)
return
# probationセグメント内のentryにアクセスした場合、protectedセグメントへ格上げする
entry.listID = 'protectedSegment'
self.probationLs.remove(entry)
self.protectedLs.appendleft(entry)
# protectedセグメントがいっぱいになったら一番古いエントリーをprobationセグメントへ移動する
if self.protectedCap > 0 and len(self.protectedLs) > self.protectedCap:
entry = self.protectedLs.pop()
entry.listID = 'probationSegment'
self.probationLs.appendleft(entry)
# probationセグメントがいっぱいで、protectedセグメントから押し出されたエントリーが入らなければprobationセグメントの一番古いエントリーを削除する
if self.probationCap > 0 and len(self.probationLs) > self.probationCap:
entry = self.probationLs.pop()
self.remove(entry)
return
def remove(self, entry):
if entry not in self.cache:
return None
del self.cache[entry]
if entry.listID == 'protectedSegment':
self.protectedLs.remove(entry)
else:
self.probationLs.remove(entry)
return entry
SLRUのまとめ
各エントリーは、Protectedセグメントに入る前に少なくとも2回アクセスされる必要があります。Protectedセグメントのエントリーは排除されてもProbationセグメントに移動するだけなので、排除されにくくなります。
そのためProtectedセグメント内のエントリーは、アクセス頻度の低いエントリーによってキャッシュから排除される可能性が低くなります。
これにより疎なアクセスパターンに弱いというLRUの欠点が解消されています。
ARC
ARCはSLRUと同様に固定サイズのLRUキャッシュ空間を分割します。
固定の割合で分割を行ったSLRUとは異なり、ARCはアクセスパターンにより動的に分割の割合を変更することが特徴です。
ARCキャッシュの管理構造

ARCではLRUキャッシュを以下の二つの領域に分割します。
T1:直近でアクセスされたエントリーを管理する
T2:アクセス頻度の高い(最低2回アクセス)エントリーを管理する
また、キャッシュ領域の動的なサイズ変更のためのデータとして以下も保持します。
B1:T1にあったけど最近アクセスがなくてT1から追い出されたもの
B2:T2にあったけど最近アクセスがなくてT2から追い出されたもの
T1+B1をL1、T2+B2をL2と呼びます。
キャッシュアクセス時の挙動について
ここではT2へ移動するためのアクセス回数の閾値を2回と仮定します。
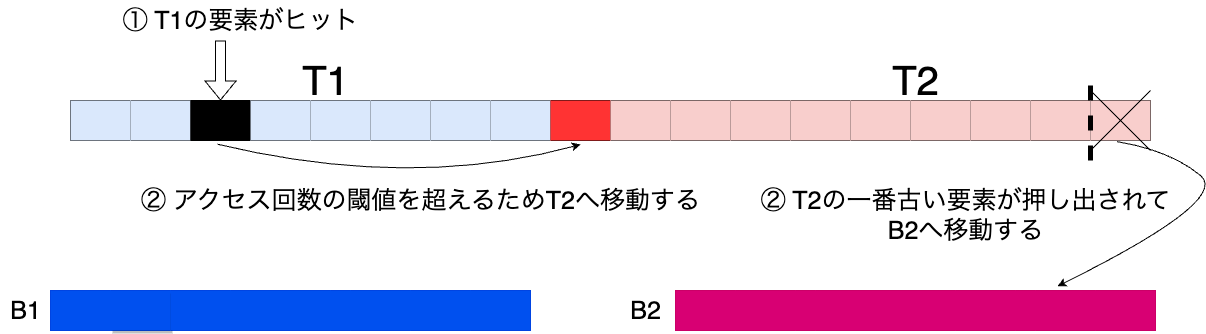
1. T1へのアクセスが起きた場合
T1領域のエントリーがアクセスされると閾値の2回を超えるため、エントリーがT2へ移動します。
また、T2の一番アクセス日時が古いエントリーがB2へと押し出されます。
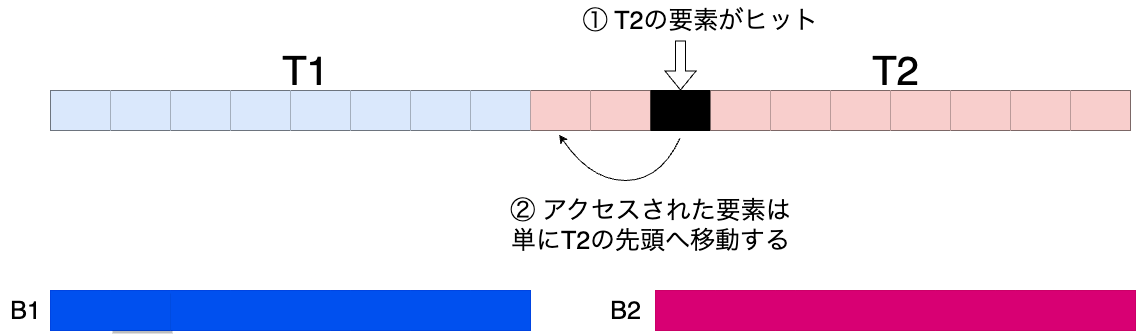
2. T2へのアクセスが起きた場合
T2領域のエントリーがアクセスされた場合は単にそのエントリーがT2で管理されるLRUの先頭に移動します。
キャッシュ領域の動的なサイズ変更について
キャッシュ領域のサイズ変更はB1, B2へのアクセスが起きた際に発生します。
以下にそのアルゴリズムを図示します。
1. B1へのアクセスが起きた場合
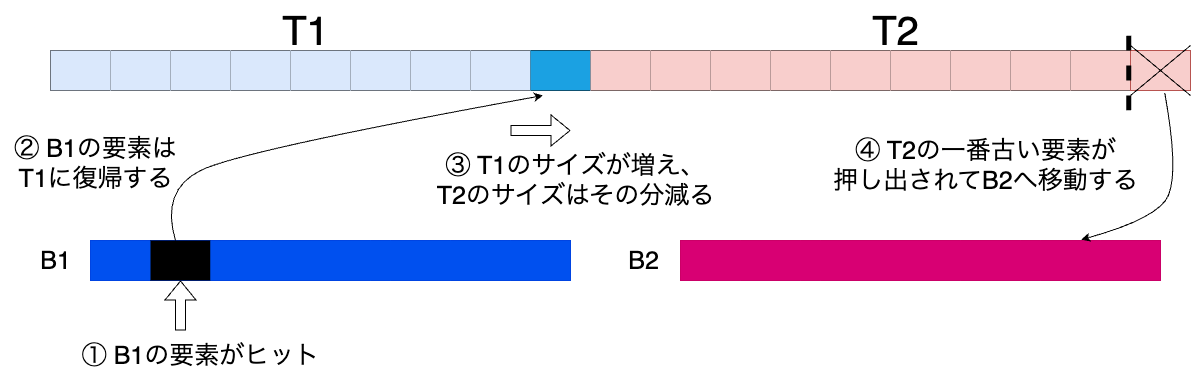
B1へのアクセスがあればB1のエントリーをT1に復帰させて、T1のサイズを1増やします。
そしてT1を増やした分、T2のサイズを減少させ、T2の一番古いエントリーをB2へ移動させます。
2. B2へのアクセスが起きた場合

B1の場合と同様です。
B2へのアクセスがあればB2のエントリーをT2に復帰させて、T2のサイズを1増やします。
そしてT1のサイズを減少させ、T1の一番古いエントリーをB1へ移動させます。
ARCの疑似コード
class ArcCache:
def __init__(self, capacity):
if capacity == 0:
raise ValueError("Cache length cannot be zero")
self.t1 = LruCache(capacity)
self.b1 = LruCache(capacity)
self.t2 = LruCache(capacity)
self.b2 = LruCache(capacity)
self.capacity = capacity
# t1領域の長さ
self.p = 0
def contains_key(self, key):
return self.frequent_set.get(key) is not None or self.recent_set.get(key) is not None
def insert(self, key, value):
# 挿入対象がすでにt1にあるならその対象をt2へ移動する
if self.t1.get(key) is not None:
self.t1.remove(key)
self.t2.insert(key, value)
return True
# 挿入対象がすでにt2にあるならt2の先頭へ移動
if self.t2.get(key) is not None:
self.t2.insert(key, value)
return True
# 挿入対象がb2にあるならt2のサイズを増やして(t1のサイズpを減らす)、対象をb2からt2に移動する
if self.b2.get(key) is not None:
if delta < self.p:
self.p -= 1
else:
self.p = 0
self.b2.remove(key)
self.t2.insert(key, value)
# b2からt2に移動した結果、t1+t2がキャッシュの容量を超えた場合、t1からb1へエントリーを移動する
if len(self.t1.cache) + len(self.t2.cache) >= self.capacity:
self.move_to_b(True)
return True
# 挿入対象がb1にあるならt1のサイズpを増やして、対象をb1からt1に移動する
if self.b1.get(key) is not None:
if delta <= self.capacity - self.p:
self.p += 1
else:
self.p = self.capacity
self.b1.remove(key)
self.t1.set(key, value)
# b1からt1に移動した結果、t1+t2がキャッシュの容量を超えた場合、t2からb2へエントリーを移動する
if len(self.t1.cache) + len(self.t2.cache) >= self.capacity:
self.move_to_b(False)
return True
# それ以外の場合、t1に挿入
self.t1.insert(key, value)
if len(self.t1.cache) + len(self.t2.cache) >= self.capacity {
self.replace(false)
}
return False
# t1->b1またはt2->b2へエントリーを移動させる
def move_to_b(self, b2_contains_key):
# insert関数の挿入対象がb2にある場合。またはt1のサイズがpを超えている場合。
if b2_contains_key or len(self.t1.cache) > self.p:
self.b1.set(self.t1.cache.keys()[0], None)
self.t1.cache.popitem(last=False)
else:
self.b2.set(self.t2.cache.keys()[0], None)
self.t2.cache.popitem(last=False)
ARCのまとめ
分割比率が固定されているSLRUとは異なり、ARCはキャッシュのアクセスパターンが変化する場合も動的に分割比率を変化させて、高いキャッシュヒット率を保つことができます。
しかし、キャッシュの管理のために4つのリストを保持する必要があり、メモリや処理のオーバーヘッド、実装の複雑性が高まるというデメリットがあります。
LIRS
LIRSは、アクセスパターンが大きなループを持つシナリオにおいて、LRUを超える性能を発揮するように設計されたキャッシュアルゴリズムです。
周期的なデータアクセスパターンにおいてループ長がキャッシュ容量より大きい場合(つまり周期内の全要素をキャッシュに収めることができない場合)、従来のLRUは最近性のみを考慮してアクセスの周期性を考慮しないため、本来はすぐにアクセスされるブロックを毎回のループで誤って退避してしまいます。
LIRSは最近性(Recency)と再利用可能距離(Inter-Reference Recency)の両方に基づいたキャッシュエントリー置換の意思決定を行うため、周期性のあるアクセスパターンにおいてLRUより優れた性能を発揮します。
LIRSキャッシュの重要な概念
1. IRR(Inter-Reference Recency)とR(Recency)について
LIRSはキャッシュのエントリごとにIRRとRを計算して、その値に応じてキャッシュ置換の判断を行うアルゴリズムです。
IRRは再利用可能距離とも呼ばれ、あるエントリの過去2回のアクセスの間に、何個の異なるエントリがアクセスされたかを示します。(エントリへの初回アクセス時にはIRRは無限大に初期化されます。)
Rは当該エントリへの最後のアクセスから現在までの間に何個の異なるエントリがアクセスされたかを示します。
言葉で説明してもわかりづらいので、実際のアクセスパターンを例に図示します。
例えば以下の図のようなキャッシュのアクセスパターンを考えてください。
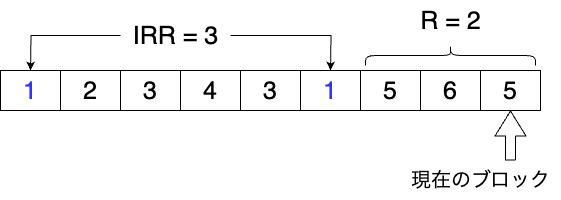
青字で示したエントリー1に対して、IRRを計算します。
エントリー1の過去2回のアクセスの間に、エントリー2,3,4,3がアクセスされています。
IRRは異なるエントリーの数を数えるので、2,3,4の3個が対象となります。
よってエントリー1のIRRは3となります。
また、Rについてはエントリー1への最後のアクセス後から現在までの間に5,6,5がアクセスされています。
IRRと同様に異なるエントリーの数を数えるので、5,6の2個が対象となります。
R=2となります。
2. LIR(Low IRR)とHIR(High IRR)
LIRSアルゴリズムは、すべてのデータエントリ-をLIR(Low IRR)とHIR(High IRR)に分類し、IRRとRの値を比較して、消去するデータ・ブロックを選択します。
IRRは定義上、値が小さいほどそのデータエントリーへのアクセス頻度が高いことを意味します。
逆に値が大きければアクセス頻度が低いことを意味します。
つまり、LIRはアクセス頻度の高いエントリーであり、HIRはアクセス頻度の高いエントリーです。
HIRのエントリーはキャッシュ中に保持されるものと保持されないものに分けられ、それぞれresident HIR, non-resident HIRと呼ばれます。
non-resident HIRはキャッシュ中に保持されませんが、そのアクセス履歴情報は記録されます。
3. その他の用語の定義
Llirs: LIRブロックの長さ
Lhirs: HIRブロックの長さ
LIRSアルゴリズム
LIRSアルゴリズムの基本的な考え方はアクセス頻度の高いLIRのエントリーをキャッシュに常駐させ、キャッシュエントリーの削除が発生したときはHIRのエントリーだけが削除されるようにするというものです。
LIRSアルゴリズムは、スタックSとキューQを用いて、実装されます。
スタックS、キューQと名付けられているものの実際はSもQもFIFOキューとして動作します。
アルゴリズムの挙動
上記の制約条件を満たすための実際のアルゴリズムは以下の通りです。
複雑なので、例を図解しながら解説します。
1. Sが満杯でないとき
新しいデータは一律にSに入力され、LIRとラベル付けされる。
2. Sで満杯であるがQが満杯でない場合
新しいデータはSとQの両方に入り、HIRとラベル付けされる。
3. SとQの両方が満杯のとき
-
新しいデータがアクセスされた場合
新しいデータがSとQの両方に入り、HIRとしてマークされる。Qの一番下にあるHIRブロックが除去される。除去されたブロックがSにも存在する場合、当該HIRブロックはnon-resident HIRに格下げされる。
例
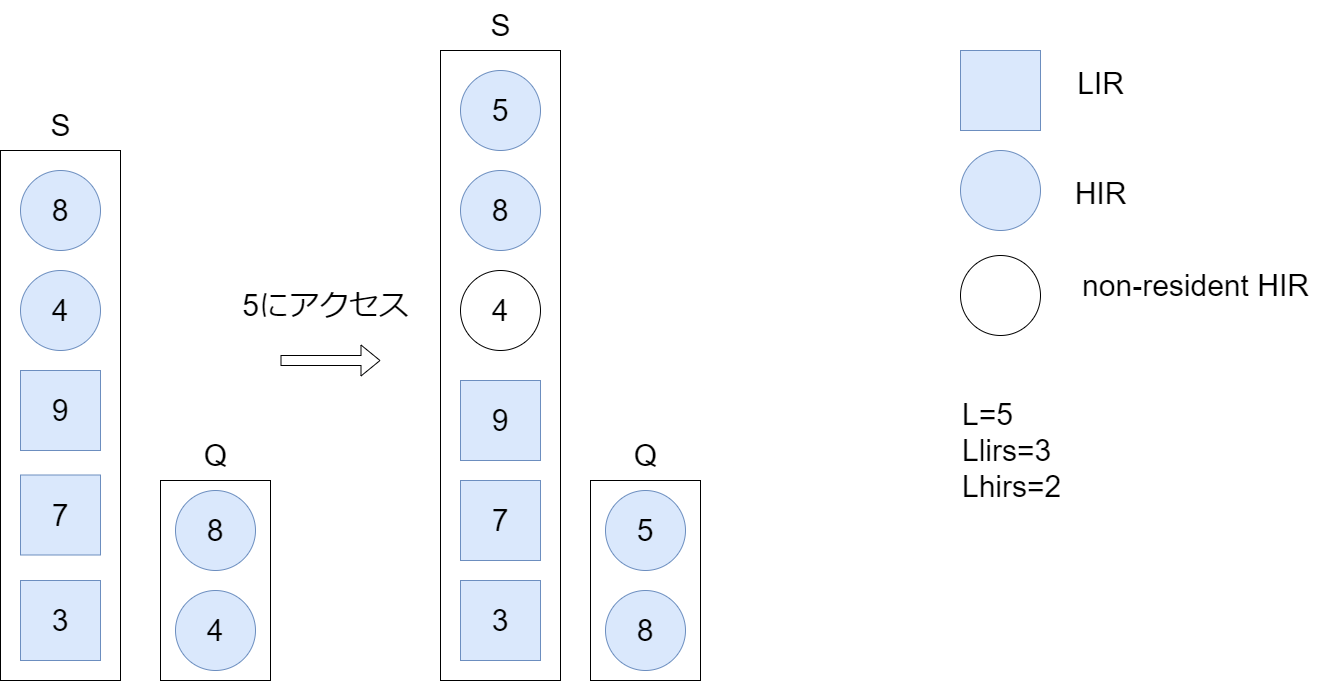
- 新たにアクセスされた5はHIRとしてSの一番上に配置されます。
- そしてQの一番下のHIRである4が削除されます。
- 削除された4はSにも含まれるためSの4がnon-resident HIRに格下げされます。
-
SのLIRブロックがヒットした場合 (LIRブロックはSにのみ存在する)
そのブロックをSの先頭に移動する。当該ブロックがSの一番下にあった場合、「スタックの刈り込み(stack pruning)」を行う(スタックの刈り込みについては後述する)
例
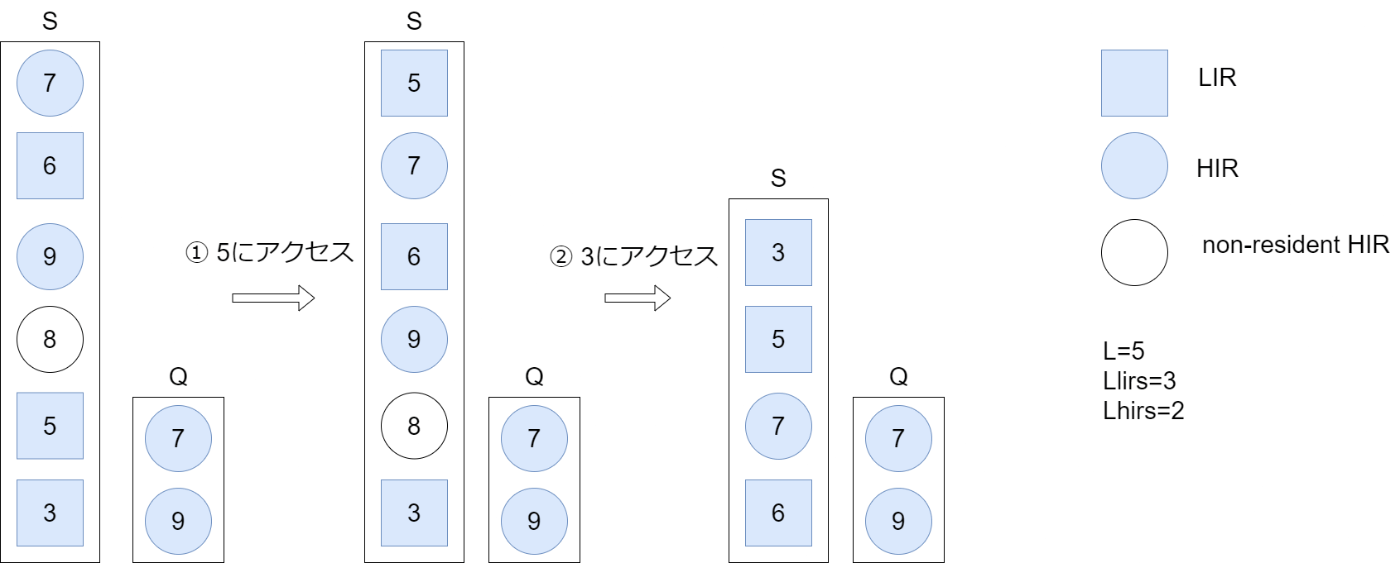
- 5がSの一番上に移動します。
- 3がSの一番上に移動します。Sの一番下がLIRではなくなるため、スタックの刈り込みにより、一番下から最も近いLIR(6)までに存在するHIRが削除されます。
-
SのHIRブロックにヒットした場合 (HIRブロックはQにのみ存在することも、SとQの両方に存在することもある)
そのブロックをSの先頭に移動させながらLIRに格上げし、Qにも一致するノードが存在する場合はQから削除する。同時に、Sの一番下にあるLIRをHIRに格下げし、Qの先頭に移動させ、「スタックの刈り込み」を行う。
例
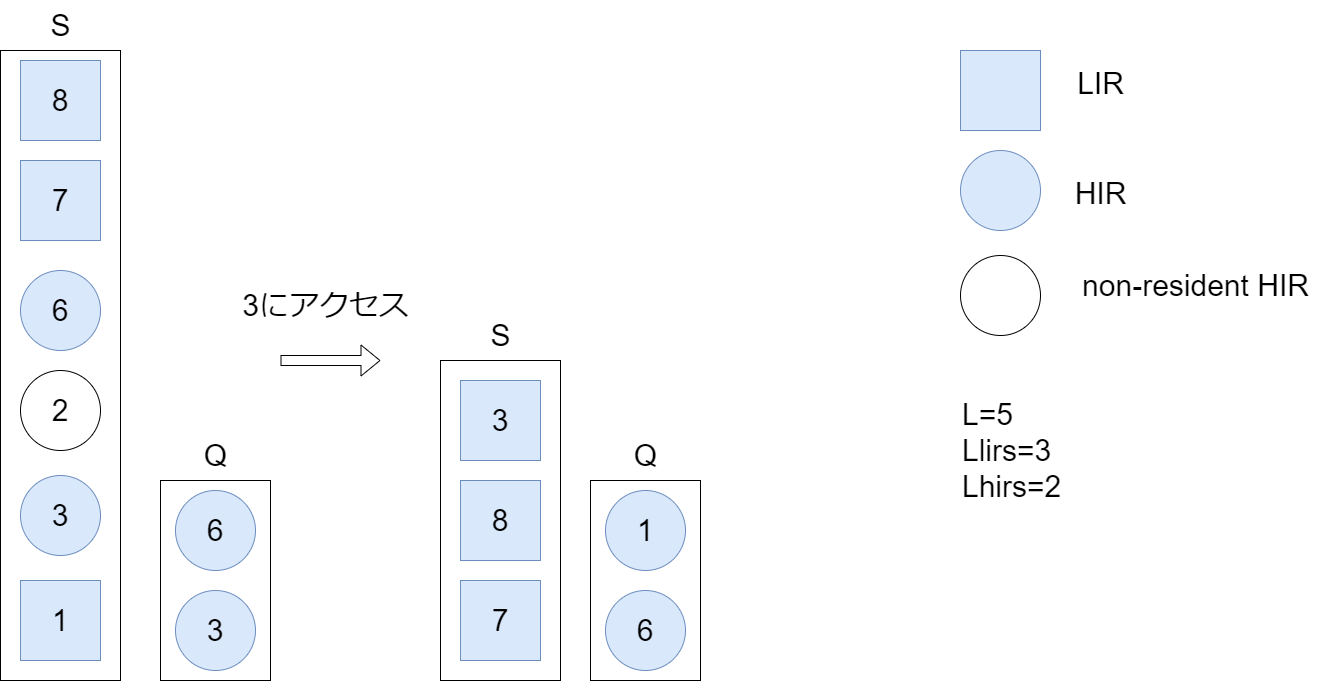
- 3はLIRに昇格してSの一番上に移動します。
- 3はQにも存在するのでQから3を削除します。
- そしてSの一番下のLIR(1)をHIRに格下げしてQの一番上に移動します。
- その後スタックの刈り込みでSの一番下から最も近いLIRである7までのHIR(3,2,6)を削除します。
-
Sに存在しないが、Qには存在するHIRブロックにヒットした場合
そのHIRブロックをQの先頭に移動する。また、このHIRブロックをスタックSの先頭に追加する。
例
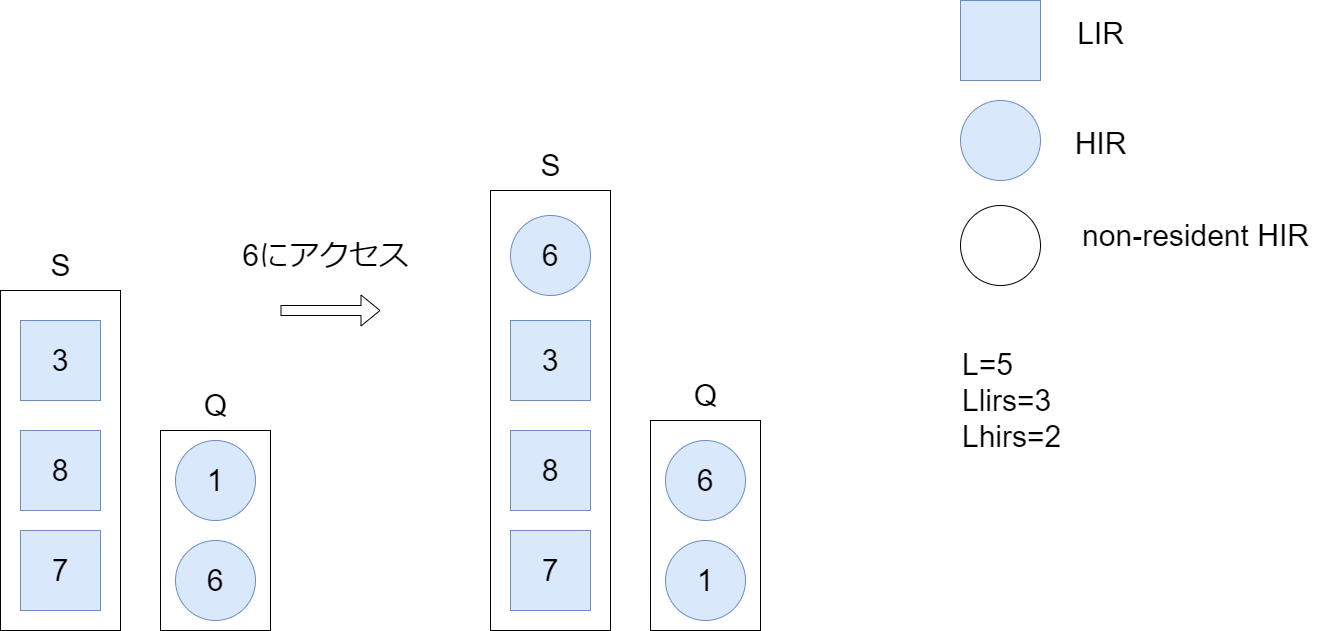
- HIRブロック6はQの先頭に移動します。
- Sの一番上にHIRブロック6を追加します。
-
アクセスされたデータブロックがS内のnon-resident HIRである場合(non-resident HIRはS内にのみ存在する。)
データブロックをLIRにアップグレードし、Sの先頭に移動する。同時にSの最下位にあるLIRをHIRにダウングレードし、Qの最後尾に移動する。
例

- non-resident HIRブロック4はLIRに昇格してSの一番上へ移動する。
- Sの最下位にあるLIRブロック3はHIRへ格下げされ、Qの一番上へ移動する。
- Qの一番下の8が追い出されて削除される。
スタックの刈り込み
Sの一番下のLIRブロックを削除する際に、HIRとnon-resident HIRのブロックをSの一番下から始めて最初のLIRブロックに出会うまで削除する操作です。
これにより、Sの最下部が常にLIRであることが保証され、制約条件の4番が満たされます。
アルゴリズムの考察
上記のアルゴリズムでは単にFIFOキューを操作するだけで明示的にIRRやR値を追跡していないのに、どうして各エントリーをLIRやHIRに分類し、HIRだけを削除対象とすることができるか疑問に思ったでしょうか?
Sでは全てのデータエントリー(LIR、HIR,non-resident HIR)は、アクセス時にLIRブロックとしてFIFOキューの先頭に移動します。
つまり、Sの一番下のエントリーは長い間アクセスされていないことがわかります。言い換えれば、Sの一番下のエントリーのIRR値はSの中で最長であることが保証されます。
そしてアルゴリズムの中ではこのSの一番下のエントリーおよびそれに連なるHIRブロックが削除対象となるため、自然にキャッシュ中のIRRが高いエントリーを削除対象とすることができているというわけです。
LIRSの疑似コード
class LIRSExecutor:
def __init__(self, lirSize, hirSize):
self.lirSize = lirSize
self.hirSize = hirSize
self.cache = []
self.S = LRU()
self.Q = LRU()
def access(self, value):
# キャッシュ中に探しているエントリが存在する場合
if value in self.cache:
location = self.S.find(value)
# Sに探しているエントリが存在する場合
if location >= 0:
state = self.S.getStateByLocation(location)
if state == 'LIR':
# アクセスしたLIRブロックをSの先頭に移動し、スタックの刈り込みを行う
self.S.movToTop(location)
self.S.stackPruning()
else:
# アクセスしたHIRブロックをLIRブロックに昇格させて、Sの先頭に移動させる。
# Sの一番下にあるLIRをHIRに格下げし、Qの先頭に移動させ、「スタックの刈り込み」を行う。
self.hitHIRInStackS(location)
self.Q.findAndRemove(value)
# Sに探しているエントリが存在しなかった場合
else:
location = self.Q.find(value)
# Qにはエントリが存在する場合
if location >= 0:
# QからそのHIRブロックを取り出してSの先頭に移動させる
# 当該HIRブロックをQの先頭に移動する
self.S.pushEntry(self.Q.getEntryByLocation(location))
self.Q.movToEnd(location)
# キャッシュ中に探しているエントリが存在しなかった場合
# キャッシュ中にその見つからなかったエントリを新たに作成する
else:
# (キャッシュ中のLIRブロックの個数)< Llirである時
if self.lirSize > 0:
# Sに当該エントリをLIRブロックとして追加する
self.lirSize -= 1
self.cache.append(value)
tmp = Entry(value, 'LIR')
self.stackS.pushEntry(tmp)
# LIRブロックはこれ以上作れないが、(キャッシュ中のHIRブロック数)< Lhirsであり、HIRブロックはまだ作れる場合
elif self.hirSize > 0:
# SとQに当該エントリをresident HIRとして追加する
self.hirSize -= 1
self.cache.append(value)
self.addAResidentHIREntry(value)
# LIRブロックもHIRブロックもいっぱいである時
else:
# Qの一番下にあるHIRブロックを除去する。
tmp = self.Q.getAndRemoveFrontEntry()
# 除去されたブロックがSにも存在する場合、当該HIRブロックはnon-resident HIRに格下げされる。
self.S.findAndSetState(tmp.rValue, 'nonResidentHIR')
if tmp.value in self.cache:
self.cache[self.cache.index(tmp.value)] = value
# 新しいデータをSとQの両方に挿入し、HIRとしてマークする。
self.addAResidentHIREntry(value)
def addAResidentHIREntry(self, value):
tmp = Entry(value, 'residentHIR')
self.S.pushEntry(tmp)
self.Q.pushToEnd(tmp)
def hitHIRInStackS(self, location):
self.S.movToTop(location)
self.S.setTopState('LIR')
self.S.setBottomState('residentHIR')
self.Q.pushToEnd(self.S.getBottomEntry())
self.S.stackPruning()
LIRSのまとめ
LIRSアルゴリズムはLRUと同じく「局所性の原理」に基づいたキャッシュ置換アルゴリズムです。つまり、最近アクセスされたエントリーは近い将来に再びアクセスされる可能性が高いという原理に基づいています。
LRUが最近性を局所性の指標として用いるのに対し、LIRSアルゴリズムはIRR(再利用可能距離)を局所性の指標として用いてキャッシュエントリーを動的にランク付けして置換の決定を行います。
これにより一般的にLIRSアルゴリズムはLRUよりも高いキャッシュヒット率を達成します。
しかし、LIRSアルゴリズムは、スタックS全体のサイズを制限せず、S内のLIRブロックの数のみをLlirsにより制限するので、連続的なキャッシュミスが発生した場合、S内のnon-resident HIRブロックの数が増加することになり、探索効率が低下する可能性があります。
まとめ
LRUの派生アルゴリズムであるSLRU, ARC, LIRSについて解説しました。
それぞれのアルゴリズムはLRUを改良して作られたものですが、決して万能ではなく特定のワークロードではLRUに性能が劣る場合も多いです。
アルゴリズムの動作原理を理解して、個別の開発ケースに応じて適切なアルゴリズムを選択することが重要になります。
次回はTiny-LFU, W-Tiny-LFUについて解説を行う予定です。
参考
Discussion