E資格対策 14-15章
14章:再帰型ニューラルネットワーク
解答した問題:
- D
- (ア)B,(イ)A,(ウ)C,(エ)B,(オ)B # オはよく分からなかったので後で要確認,コード確認
- D
- (ア)A,(イ),(ウ)A,(エ)B,(オ)A ※イが分からなかったため要確認
- (ア)A,(イ)C,(ウ)B
- B ※要確認
- C
- (ア)C,(イ)A,(ウ)B,(エ)B,(オ)D,(カ)A ※全体的に不明瞭だから要復習
間違えた問題:
2. (ア)B⇒C ※コードと逆伝播確認
4. (イ)B,(オ)A⇒B
5. (ア)A⇒C
6. B⇒A
8. (ア)C⇒A
再帰型ニューラルネットワーク(RNN)の特徴
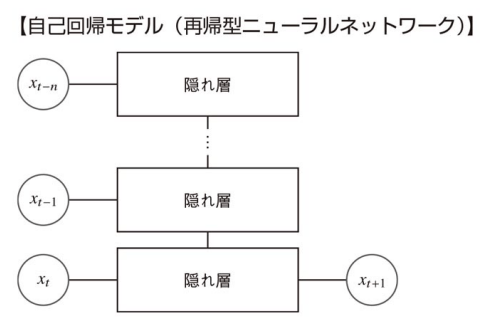
- 時刻毎の
x - 入力される
x - 再帰型ニューラルネットワークの誤差逆伝播法による計算は時系列方向に勾配が遡っていくため,バックプロパゲーション・スルー・タイム(BPTT:BackPropagation Thtough Time) と呼ばれる。
- 系列長が長くなると勾配爆発・勾配消失が起きやすくなるため,活性化関数としてsigmoid関数やtanh関数が使われることが多い。
誤差逆伝播
- 時系列T個のRNNレイヤを連結したネットワークにおいて,出力が2つに分岐しているため逆伝播では各勾配が合算されて伝わる
出力層から伝わる勾配dy_{t}+次の隠れ層から伝わる勾配dh_{t} - 時系列T個のRNNレイヤ連結したネットワークは同じ重みを使用しているため,最終的な入力値の重みに対する勾配は各RNNレイヤの重みの勾配を足し合わせたものになる。
\frac{\partial L}{\partial W_x} = \sum_{t=1}^T dh_t \cdot x_t^T
ここで,
dh_t = \frac{\partial L}{\partial h_t}= \frac{\partial L}{\partial y_t} \cdot \frac{\partial y_t}{\partial h_t} + \frac{\partial L}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial h_t}
ここで,
\frac{\partial y_t}{\partial h_t} = W_y
\frac{\partial h_{t+1}}{\partial h_t} = \phi'(a_t) \cdot W_h
※
勾配クリッピング
勾配爆発を回避するための方法として勾配クリッピングがある。
勾配クリッピングとは,勾配の値が大きくなりすぎないように調整することの総称である。例えば,要素毎にクリッピングする方法や全ての要素を一律にクリッピングする方法等がある。
(以下は全ての要素を一律にクリッピングする方法の例。
ゲート
- ゲート付き再帰型ニューラルネットワークにおけるゲートとはデータを通過させる割合を求める機構である。
- ゲートの活性化関数には出力が0~1に制約されるシグモイド関数がよく用いられる。
- ゲートには2つの入力と1つの出力があり,入力2はシグモイド関数を通ることで各要素が0~1となり,これと入力1とのアダマール積が出力となる。

スキップ接続
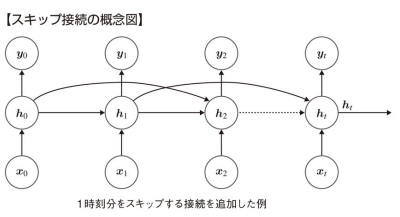
- 長期依存性の課題への対策のひとつとして隠れ層を1時刻以上スキップさせた接続を追加する方法をスキップ接続という
リーキーユニット(leaky unit)
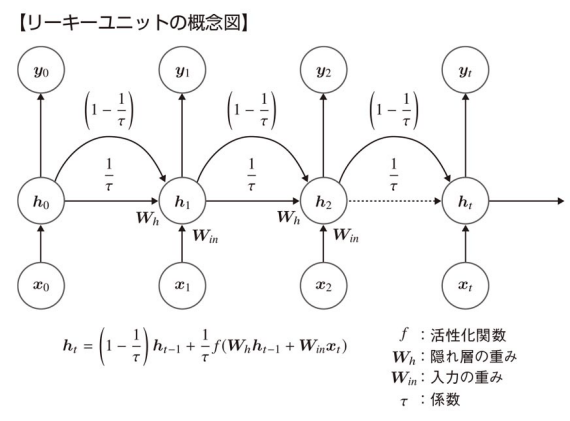
- 隠れ層に線形結合を導入して移動平均の効果を得る。このような線形結合を持った隠れユニットをリーキーユニットと言う。前層から伝わった隠れ層に
1-\frac{1}{\tau} \frac{1}{\tau} - リーキーユニットの効果:
-
勾配消失問題の軽減:
リーキーユニットは、以前の隠れ状態 (h_{t-1}) の影響を一定割合で保ち続けるため、時間が経過するにつれて隠れ状態が完全に消失することを防ぎます。これにより、長期依存関係の学習が容易になります。 -
情報の持続性の向上:
リーキーユニットは、前の状態をある程度保持し続けるため、RNNが過去の情報をより長く保持できるようになります。これにより、長期の依存関係を持つデータの学習が改善されます。 -
安定した学習:
(\alpha) を適切に設定することで、RNNが学習中に過度に振動することなく、安定して訓練されるようになります。これにより、モデルの収束速度が向上することがあります。
-
LSTMの構造
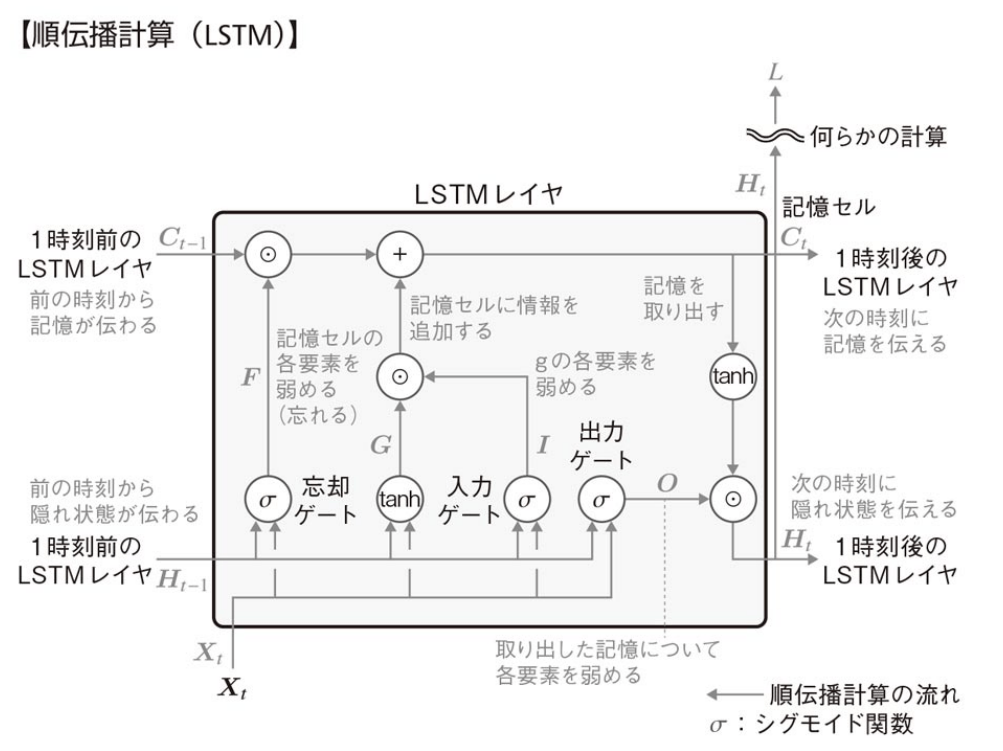
構成要素

LSTMは3つのゲートと記憶セルで構成される。各ゲートは入力値
ここで,上段には,記憶
- 出力ゲート:
- 取り出した記憶について,各要素を弱める(忘れる)度合いを決めるゲート。
- 出力ゲートの出力値
O
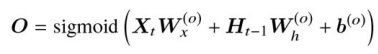
- 忘却ゲート:
- 記憶セルの各要素を弱める(忘れる)度合いを決めるゲート。
- 忘却ゲートの出力値
F
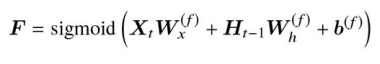
- 入力ゲート:
- 記憶セルに追加される
G - 記憶セルに追加される,入力と隠れ状態を結合した後の値
G
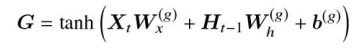
- 入力ゲートの出力値
I
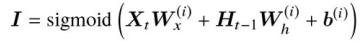
- 記憶セルに追加される
- 記憶セル:
- 過去の情報を記憶する部分。
記憶C_t H_t
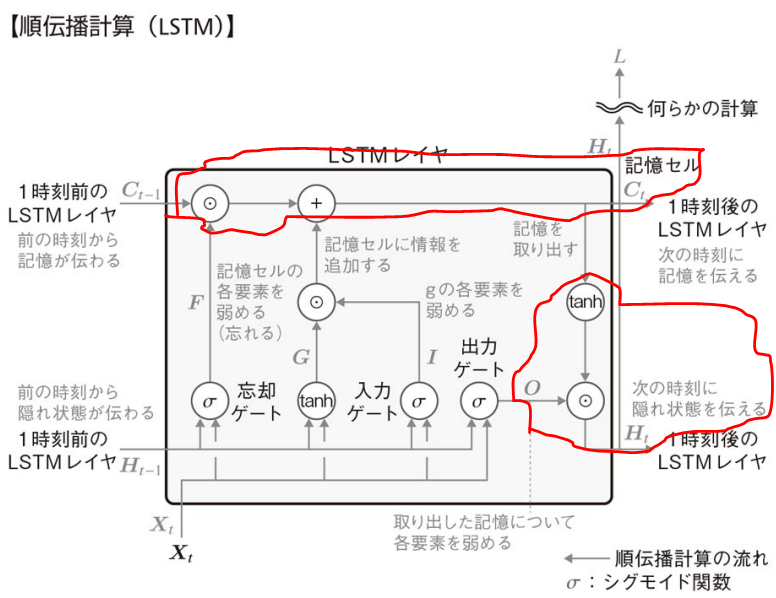
上記で述べた構成要素や前層から伝わる記憶
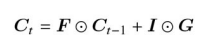
以上により算出された記憶

参考: 覗き穴結合
ゲートの値は,上記では入力値
具体的に,上記の
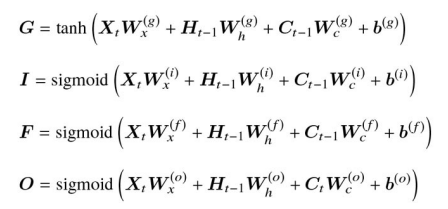
覗き穴結合の計算は,
利点:
- 長期的な情報をより効率的に勝つようできるため,依存関係をモデリングする上で精度向上が望める。
- 各ゲート出力値がより精緻になる。
欠点:
- パラメータ数・計算コストが増加。
- パラメータが増加するため,過学習のリスクが高まる。適切な正則化が必要。
GRU
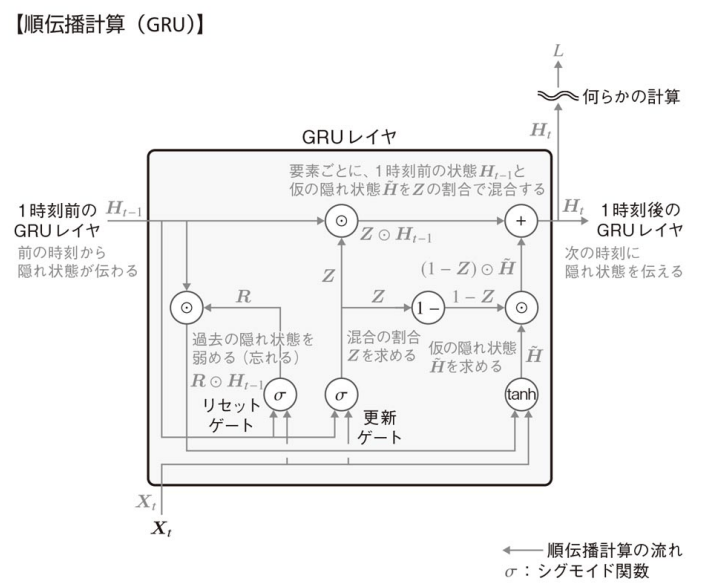
GRUはLSTMとは異なり,直接的に長期記憶の役割を担うセルは存在せず,隠れ状態にその長期的な記憶を蓄えるような工夫がなされている。また,パラメータ数もLSTMに比べて少ない。
構成要素
GRUは主にリセットゲートと更新ゲートの二つのゲートで構成される。
- リセットゲート:
- 過去の隠れ状態を弱める程度を決めるゲート。
- リセットゲートの出力値
R
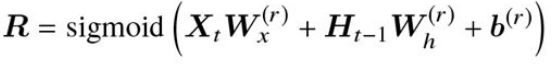
- 更新ゲート:
- 過去の隠れ状態と仮の隠れ状態の混合割合を決めるゲート。
- 更新ゲートの出力値
Z
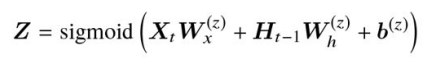
計算の流れ
-
仮の隠れ状態
\tilde{H}
リセットゲートの出力値R H_{t-1}
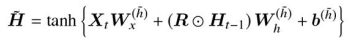
-
隠れ状態
H_t
仮の隠れ状態\tilde{H} Z H_{t-1}

前層からの隠れ状態の値と計算した仮の隠れ状態の値を,更新ゲートの値を基にどういう配分で隠れ状態に反映させるかを決めている。
双方向RNN

RNNはある状態の中間層の出力値を次の状態(未来の状態)に順伝播するネットワークである一方で,双方向RNNは中間層出力を次の状態への順伝播と前の状値への逆伝播の両方向に伝播するネットワークである。双方向RNNでは学習時に過去(前の状態)と未来(次の状態)の情報の入力を必要とすることから,運用時(推論時)も過去から未来までの全状態を入力して初めて予測できるようになる。
-
過去の状態からの順伝播計算:
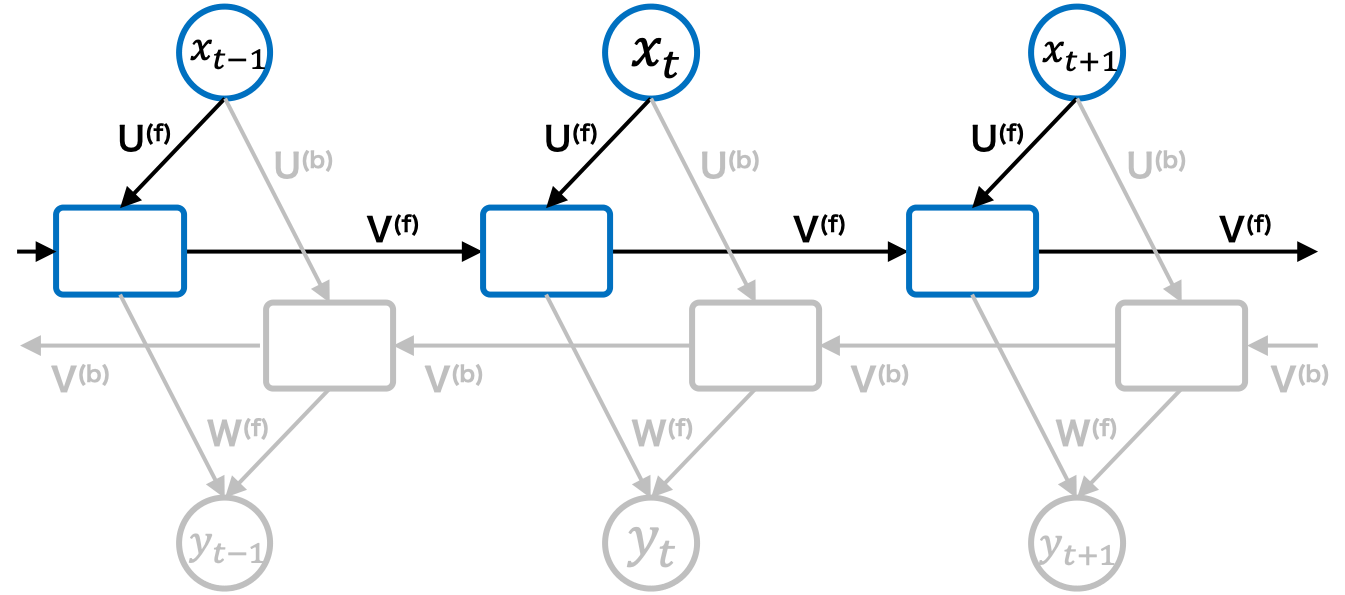
過去の状態からの順伝播では状態t x_t t-1 z_{t-1} U^{(f)} V^{(f)} \phi(\overrightarrow{z}_{t})
\overrightarrow{z}_t=U^{(f)}x_{t}+V^{(f)}z_{t-1}+b^{(f)}_z -
未来の状態からの順伝播計算:
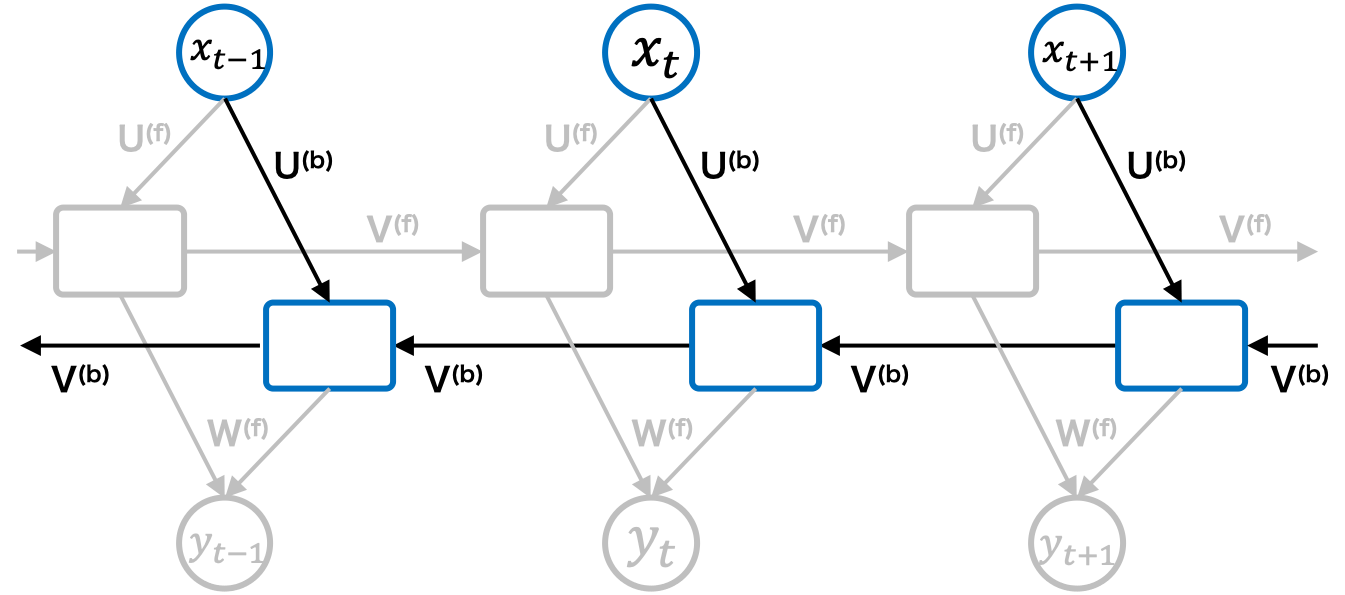
未来の状態からの順伝播計算では状態t x_t t+1 z_{t+1} U^{(b)} V^{(b)} \phi(\overleftarrow{z}_{t})
\overleftarrow{z}_t=U^{(b)}x_{t}+V^{(b)}z_{t-1}+b^{(b)}_z -
出力層の計算:
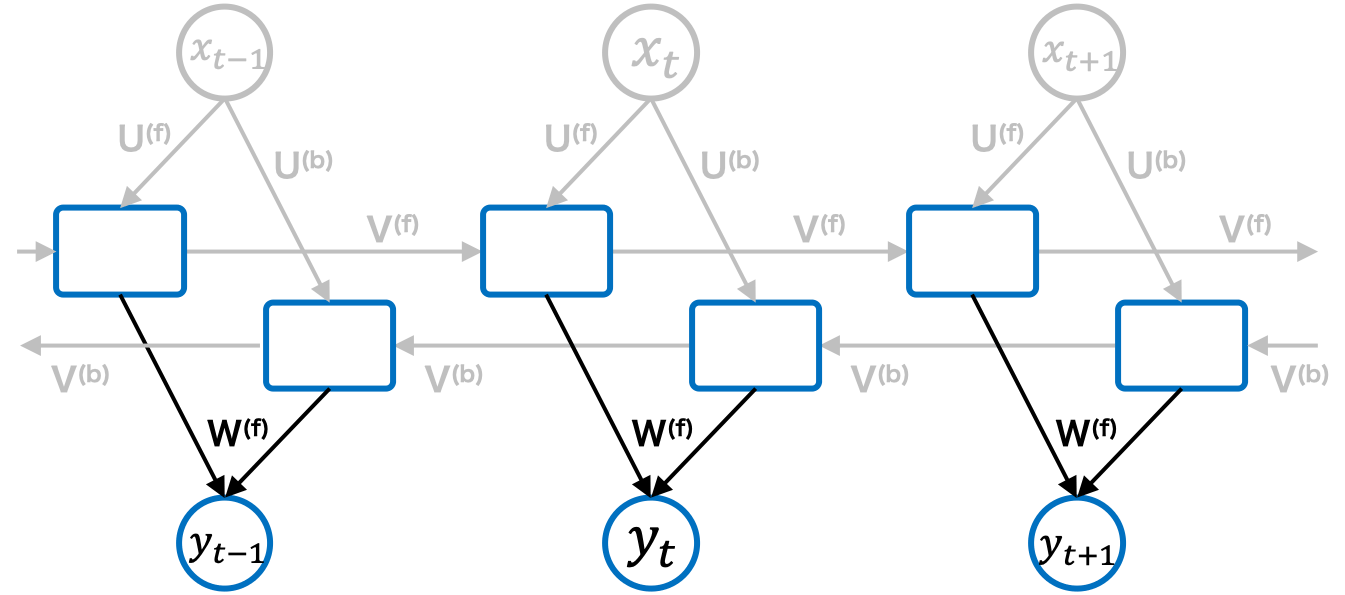
先の計算で伝播してきた2つのベクトル
実装⇒https://github.com/keras-team/keras/blob/v3.3.3/keras/src/layers/rnn/bidirectional.py#L10-L326
model = keras.Sequential()
model.add(
layers.Bidirectional(layers.LSTM(64, return_sequences=True), input_shape=(5, 10))
)
model.add(layers.Bidirectional(layers.LSTM(32)))
model.add(layers.Dense(10))
model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
bidirectional (Bidirectiona (None, 5, 128) 38400
l)
bidirectional_1 (Bidirectio (None, 64) 41216
nal)
dense_3 (Dense) (None, 10) 650
=================================================================
Total params: 80,266
Trainable params: 80,266
Non-trainable params: 0
系列変換モデル
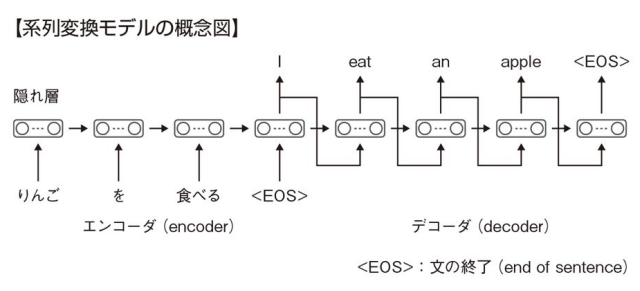
- 上図に示す通り,系列変換モデルにはエンコーダ用の再帰型ニューラルネットワークとデコーダ用の再帰型ニューラルネットワークがある。
- 系列変換モデルの特徴として以下がある。
- 入力系列{りんご,を,食べる}と出力系列{I,eat,an,apple}の長さは一致しなくてよい。
- 系列の長さはデータによって異なっていてもよい。例: {りんご,を,食べる}のデータの次に{私,は,りんご,を,食べる}というデータが入力されても動作する。これは,タイムステップ毎に同じ重み
W_x, W_h
教師強制

- RNNやSeq2Seqモデル等を訓練するとき次のタイムステップの入力として自身の出力を使用するが,初期段階では予測が不正確であることが多い。これによって誤った予測が次のステップの入力として使用され,その結果,さらに誤った予測が続く「誤差の蓄積」が発生する。
- 教師強制とは,以上課題を解決するための手法であり,具体的には,訓練時にモデルが次のステップの入力として実際の訓練データの値(ターゲット値)を使用する方法。
- メリット: モデルがより早く収束する,誤差の蓄積が防げるため安定した学習が可能
エコーステートネットワーク
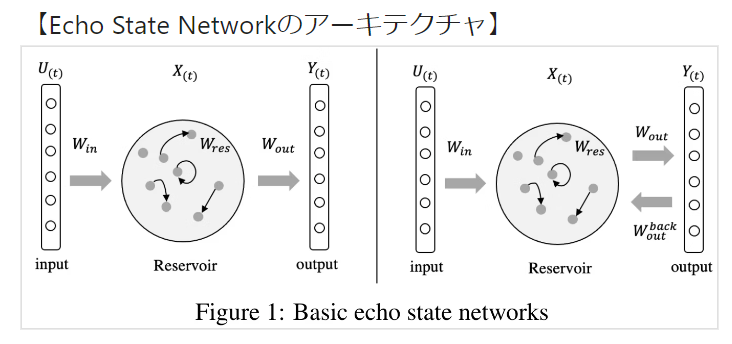
- エコーステートネットワークとは,時系列データに対する高速機械学習手法である。エッジコンピューティングのように時系列データストリームの速度に合わせてリアルタイムにモデルを更新する必要があるケースで有用。
- 入力層とリザバー(隠れ層)を通して高次元空間へ非線形写像しつつ,RNN構造で時系列情報を取得することで出力層(Ridge回帰)の予測を手助けする。
- 入力の重みとリザバー(隠れ層)の重みをランダムな値で固定して出力の重みのみを学習する。
Attention
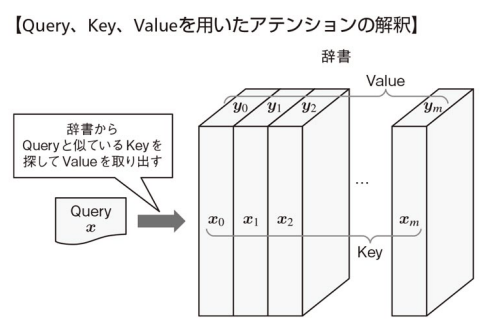
アテンションの概要
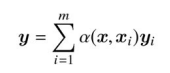
-
-
-
- 上式は,**m個の訓練データ
{(x_i, y_i)}^m_{i=1} x y \alpha x x_i y_i y_i
ソフト・アテンション
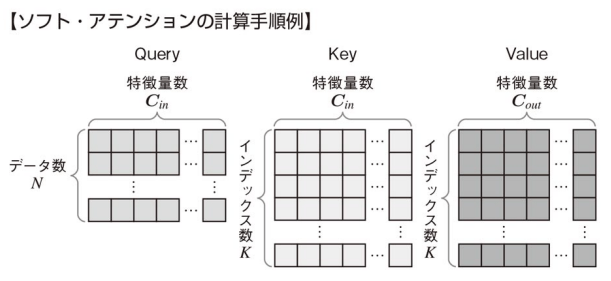
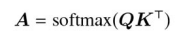
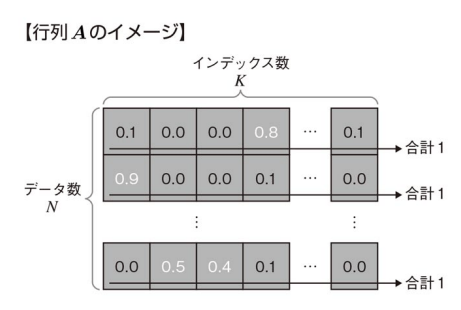
- Query:
データ数N×特徴量数C_{in} Q - Key:
辞書のインデックス数K×特徴量数C_{in} K - Value:
辞書のインデックス数K×特徴量数C_{out} V
この行列
- 入力としての単語埋め込み(word embeddings)は特定の次元数
を持ちますが、最終的な出力として生成される特徴量や埋め込みは、タスク(例えば、次の単語の予測や翻訳など)に応じて異なる次元数 C_{in} を持つことがある。 C_{out} - データ数は検索文として関連付けしたいデータを選んでいる。
グローバル・アテンション
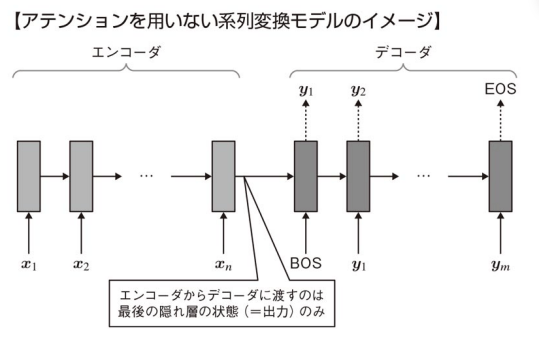
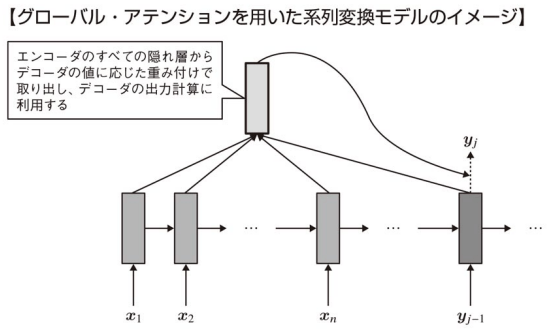
図の薄いグレー部分がエンコーダ,濃いグレー部分がデコーダを表す。エンコーダ側では入力系列
が与えられ,デコーダ側では出力系列 x_1,x_2,...,x_n が得られている。BOSとEOSはセンテンスの最初と最後を表す。 y_1,y_2,...,y_m
アテンションを用いない系列変換モデルは長い系列のデータを学習することが難しく,初期に入力された情報がデコーダまで伝わり辛くなるという問題がよく生じる。
そこで,各デコーダの出力を計算する際に全てのエンコーダの隠れ層の出力を用いるグローバル・アテンションが用いられる(系列変換モデルにアテンションを適用したモデルの一つ)。
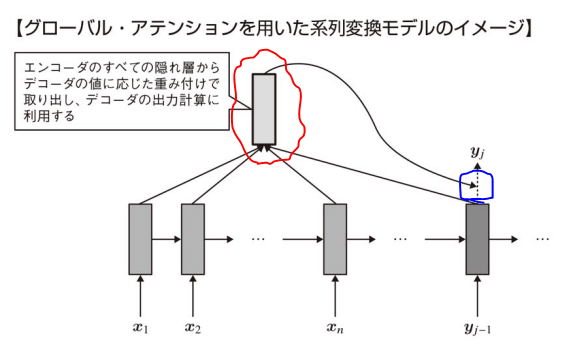
以上図の赤枠で囲った箇所は以下式で表される。以下式中の
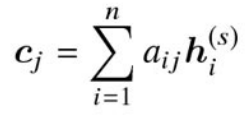
ここで,式中の
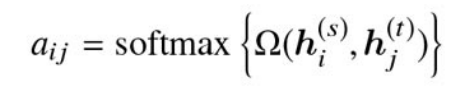
シーケンス内の各位置(トークン)に対してどれだけ注目すべきか(重み)を計算するため,各位置に対して1つの重みが割り当てられる。そのため,shapeは
になる。(隠れ層のノード数方向にsumをとって,各トークン毎のレイヤから値を一つ出すイメージ) N×T
ここで,

つまり,赤枠で囲った箇所はデコーダの
15章:深層学習を用いた自然言語処理
回答した問題:
- ア:B,イ:A,ウ:A,エ:C,オ:D
- ア:A,イ:B,ウ:D,エ:D,オ:B,カ:A,キ:A ※分からない
- ア:B,イ:D,ウ:B,エ:B,オ:A
- ア:C,イ:B,ウ:B,エ:D,オ:A
- ア:C,イ:A,ウ:A,エ:A,オ:C,カ:D,キ:A ※分からない
- ア:A,イ:B,ウ:D,エ:A,オ:B,カ:,キ:,ク: ※分からない
間違えた問題:
2. 大体全部×
3. 間違ってないけど要復習
4. イ:B→D
5. イ:A→B,エ:A→B,オ:C→B
6. 大体全部×
word2vec
- word2vecとは単語埋め込み(Word Embedding)やある語彙の単語やフレーズ群を分散表現へと写像ニューラルネットワークを学習しておき,その埋め込み後ベクトルを入力として各種の機械学習予測を行うための特徴選択手法を指す。
- word2vecは3層MLPで中間層にベクトル表現(300次元程度)が獲得できる。ネットワーク構造以下2種類がある。通常以下モデルの出力層では全ての語彙を対象としてソフトマックス関数と交差エントロピー誤差関数を計算する。
- CBOW: 周辺単語から対象となる1単語を予測するモデル。
- skip-gram: 対象となる1単語から周辺単語を予測するモデル。
- 3層MLPでは入力層側の重み
W_{in} W_{out} W_{in}
負例サンプリング
負例サンプリングを適用した場合の出力層では1個の正例と
-
k - 全ての語彙を対象としてソフトマックス関数を計算することに比べ,負例サンプリング適用時は
k+1 -
k P(w_i)

GNMT(Google's Neural Machine Translation System)
GNMTはGoogle社が開発したニューラル機械翻訳システム。2016年から実際のサービスに利用されている。以下図の通り,エンコーダ,デコーダ,アテンションから構成されている。
このモデルは非常に強力であり,「ポルトガル語→英語」および「英語→スペイン語」の期間翻訳を行ったGNMTモデルを用いると「ポルトガル語→スペイン語」の正解ラベルのペアを1つも与えずにポルトガル語→スペイン語の機械翻訳を行うことができた"ゼロショット学習"の例が報告されている。
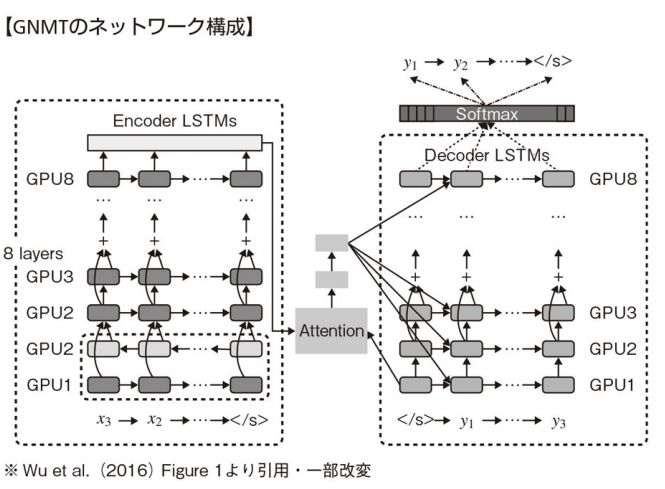
GNMTに採用された工夫は主に以下である。
- LSTMレイヤの多層化: エンコーダ・デコーダ共に8層で構成されている
- 双方向LSTM層: エンコーダの1層目のみ双方向LSTMになっている。エンコーダの1段目と2段目を合わせた部分を1層目と呼んでいる。
- スキップコネクション
- 複数GPUでの分散学習: 8層のエンコーダおよびデコーダに対して1層毎に1個のGPU(計16個)を割り当てている。また,語彙数によっては8個のGPUをエンコーダとデコーダの両方で用いる場合もある。※エンコーダの1層のみが双方向LSTMであるため,他の層は前の層の計算が完全に終了する前に計算を開始することができる(全ての層を双方向LSTMにした場合,それぞれの層は前の層の順方向と逆方向の計算が終わるのを待たなければならず,2GPUしか並列に動かせない)。
- アテンションの利用: デコーダ側の最下層(第1層)の出力とエンコーダ側の最上層(第8層)とを接続して計算する。デコーダ側の時間ステップ
i i+1
複数GPUによる並列化
GNMTではモデル並列化と同時にデータ並列化も行っている。データ並列では,重みの更新は非同期型で行う。
- 同期型: パラメータを更新する際,全てのGPUワーカの順伝播および逆伝播を待つ必要があるため,スループットが低い。
- 非同期型: パラメータを更新する際,他のワーカを待つ必要がないため,スループットが高い。しかし,古いモデルの勾配で更新することがあり得るため,学習が不安定になることがある。
モデル並列
モデル並列(Model Parallelism)は、大規模なディープラーニングモデルを複数のデバイス(通常はGPU)に分割し、それぞれのデバイスがモデルの異なる部分を並行して処理する技術です。これは、モデルが非常に大きくて1つのGPUのメモリに収まらない場合や、計算負荷を分散して訓練速度を上げたい場合に用いられます。
モデル並列は、同じモデルを複数のデバイスで並行して動かす**データ並列(Data Parallelism)**とは異なり、モデル自体を物理的に複数のデバイスに分割して処理します。これにより、巨大なモデルを複数のGPUのメモリに分散させることができ、より大規模な計算が可能になります。
2. モデル並列が必要な理由
モデルが非常に大きい場合、1つのGPUのメモリにモデル全体を載せることができないことがあります。例えば、トランスフォーマー(Transformer)や大規模なニューラルネットワークは、数十億のパラメータを持つことがあり、これを単一のGPUで処理するのは不可能な場合があります。
また、モデル並列を使用することで、複数のデバイスにモデルの計算負荷を分散させることができるため、より効率的に計算を行うことができます。
3. モデル並列の実装方法
モデル並列には、主に2つの実装方法があります。
(1) レイヤーごとの分割
モデルをレイヤーごとに分割し、異なるレイヤーを異なるデバイスで処理する方法です。例えば、最初の数レイヤーをGPU 1で、次の数レイヤーをGPU 2で処理します。
- 利点: 実装が比較的シンプルで、モデルの自然な層構造に基づいて分割できるため理解しやすいです。
- 欠点: 各デバイスが処理を終えるまで次のデバイスが計算を待つ必要があり、GPU間の通信がボトルネックになることがあります。
具体例: 例えば、ディープニューラルネットワークを5層に分け、次のように分割することが考えられます。
- GPU 1: 第1層と第2層
- GPU 2: 第3層と第4層
- GPU 3: 第5層
データがGPU 1で処理された後、その結果がGPU 2に渡され、さらに処理が続きます。
(2) テンソルの分割
モデルの中のテンソル(重み行列やバイアス行列など)を部分的に分割し、それぞれのテンソル部分を異なるデバイスで並列に処理する方法です。この方法は、モデルの大きなテンソルを各GPUに分散させ、全体の計算を効率化します。
- 利点: 大規模なテンソルを並列処理できるため、計算速度の向上が期待できます。
- 欠点: テンソルの分割と再結合には通信オーバーヘッドが伴い、実装が複雑になることがあります。
具体例: 大規模な全結合層や畳み込み層の重み行列を2つのGPUに分割し、それぞれで並列に処理します。計算後、それぞれの結果を結合して次の処理に進むという流れになります。
4. モデル並列の応用シナリオ
モデル並列は、次のような状況で特に有用です。
-
超大規模モデル: GPTやBERTのような数十億パラメータを持つ巨大なモデルでは、1つのGPUのメモリにモデル全体をロードできません。モデル並列を使えば、モデルを分割して複数のGPUで処理できるため、より大きなモデルの訓練や推論が可能になります。
-
大規模畳み込みニューラルネットワーク(CNN): 畳み込み層のカーネルやフィルタが非常に大きい場合、その重み行列やバイアスを分割して並列処理することで、効率的に計算を行えます。
-
トランスフォーマーモデル: トランスフォーマーのような深いモデルでは、アテンションメカニズムやフィードフォワード層を分割して各GPUで並行して計算することができます。
5. モデル並列の課題
モデル並列を実装する際には、いくつかの課題があります。
(1) 通信オーバーヘッド
モデルの異なる部分が異なるGPUに分割されるため、各GPUが計算結果を次のGPUに渡す際に通信が必要です。この通信オーバーヘッドが大きくなると、モデル並列のメリットが減少し、全体の訓練速度が低下する可能性があります。
(2) 負荷分散の難しさ
モデル並列では、各GPUに対する計算負荷が均等でないと、特定のGPUが他のGPUよりも早く処理を終えて待機状態になる可能性があります。これにより、計算リソースが効率的に使用されないことがあります。
(3) 同期の必要性
各GPUが異なる部分の計算を行うため、計算結果を正しく統合するためには各GPUの処理が同期される必要があります。この同期が不適切だと、計算が正しく行われないか、速度が低下する原因となります。
6. モデル並列の実装例
ディープラーニングフレームワーク(PyTorch、TensorFlowなど)は、モデル並列をサポートしており、実装が比較的簡単です。
(1) PyTorchでのモデル並列
PyTorchでは、torch.nn.Module クラスの to() メソッドを使って、モデルの各部分を異なるデバイスに転送し、モデル並列を実装できます。
import torch
import torch.nn as nn
# シンプルな2層のモデル
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.layer1 = nn.Linear(10, 50).to('cuda:0') # GPU 0 に配置
self.layer2 = nn.Linear(50, 1).to('cuda:1') # GPU 1 に配置
def forward(self, x):
x = self.layer1(x)
x = x.to('cuda:1') # GPU 0 -> GPU 1 へ転送
x = self.layer2(x)
return x
# モデルとデータ
model = MyModel()
data = torch.randn(32, 10).to('cuda:0') # データは GPU 0 に配置
# 前向き計算
output = model(data)
このコードでは、layer1 を GPU 0 に、layer2 を GPU 1 に配置しており、データを異なるGPUに転送しながら計算しています。
(2) TensorFlowでのモデル並列
TensorFlowでは、tf.distribute.Strategy を使ってモデル並列を実装できます。具体的には、tf.distribute.MirroredStrategy や tf.distribute.experimental.ParameterServerStrategy を使用して、複数のGPUでモデルのパラメータやレイヤーを分散処理できます。
import tensorflow as tf
# Strategyの設定
strategy = tf.distribute.MirroredStrategy()
with strategy.scope():
# モデルの定義
model = tf.keras.Sequential([
tf.keras.layers.Dense(50, input_shape=(10,)),
tf.keras.layers.Dense(1)
])
# モデルのコンパイル
model.compile(optimizer='adam', loss='mse')
# データと訓練
data = tf.random.normal([32, 10])
labels = tf.random.normal([32, 1])
# 訓練実行
model.fit(data, labels)
このコードでは、`MirroredStrategy
` によってモデルを複数のGPUに自動的に分割し、並列計算を行っています。
7. モデル並列の実例
モデル並列は、次のようなシナリオで効果を発揮します。
-
GPTやBERTのような巨大なモデル: 数十億パラメータを持つ巨大な言語モデルは、単一のGPUに収まらないことが多いため、モデル並列を使用して計算を効率化します。
-
自動運転やロボット工学のシステム: 複数のセンサーデータや画像データを同時に処理する必要があるモデルにおいて、モデル並列を使って複数の処理を同時に行います。
まとめ
モデル並列は、巨大なディープラーニングモデルを複数のデバイスに分割して効率的に処理するための技術です。モデルの計算負荷を複数のGPUに分散させることで、メモリ制約を回避し、計算速度を向上させることができます。ただし、通信オーバーヘッドや負荷分散の課題があり、これらを適切に管理することが成功の鍵となります。
データ並列
データ並列は、同じモデルのコピーを複数のデバイス(通常はGPU)に配置し、異なるデータバッチに対して同時に計算を行う手法です。各デバイスは同一のモデルに対して独立して訓練や推論を行い、その後、計算結果を統合して最終的なモデル更新を行います。
データ並列は、モデル自体が1つのデバイスに収まるが、訓練に使用するデータのサイズが非常に大きい場合や、複数のデバイスで訓練を高速化したいときに使われます。
2. データ並列の基本的な流れ
データ並列の典型的な流れを順を追って説明します。
-
モデルの複製:
まず、同じモデルを複数のデバイス(GPUなど)にコピーします。これにより、各デバイスに同じモデル構造とパラメータが存在します。 -
データの分割:
訓練データを複数のバッチに分割し、各デバイスに異なるバッチを送ります。例えば、バッチサイズが128で、4つのGPUを使用している場合、各GPUに32個ずつのデータが割り当てられます。 -
計算の実行:
各デバイスで、それぞれのバッチに対して前向き伝播(forward propagation)、損失の計算、後向き伝播(backward propagation)を行います。各デバイスは独立して計算を行い、その結果を使って勾配を計算します。 -
勾配の統合:
各デバイスで計算された勾配を中央のデバイス(マスター)に集めて統合します。これを「勾配の平均化」といいます。すべてのデバイスで計算された勾配を平均して1つの勾配にまとめます。 -
モデルの更新:
統合された勾配を使って、すべてのデバイスにあるモデルのパラメータを同時に更新します。この更新は、通常、分散型のオプティマイザ(例: AdamやSGDなど)を使用して行います。 -
繰り返し:
データバッチの処理とモデル更新を繰り返して、モデルが訓練されます。
3. データ並列の利点
データ並列にはいくつかの利点があります。
-
訓練速度の向上: 複数のデバイスを使ってデータバッチを並行して処理することで、訓練速度を大幅に向上させることができます。特に、データセットが大規模な場合、データ並列は効果的です。
-
大規模データセットの効率的な処理: 巨大なデータセットを一度に1つのGPUで処理することが難しい場合、データを複数のデバイスに分散させることで、効率よく処理ができます。
-
メモリの効率的な使用: モデル自体は各デバイスで同じものが使われるため、データに対して効率的にメモリを利用できます。デバイスごとに独自のメモリ空間でモデルとデータを扱うことができるため、1つのGPUのメモリに依存する必要がありません。
4. データ並列の課題
データ並列にもいくつかの課題や問題点があります。
(1) 通信オーバーヘッド
各デバイスが計算を行った後、勾配をマスターに集めて平均化し、再度モデルを更新して各デバイスに送信する必要があります。このようなデバイス間の通信には時間がかかり、特に大量のデバイスを使用する場合、この通信オーバーヘッドが全体の訓練速度を制約する可能性があります。
- デバイス数が増えると通信時間が増加: 訓練に使うデバイスの数が増えるほど、各デバイスからの勾配を集めて平均化する時間が増えるため、通信オーバーヘッドが問題となります。
(2) 同期問題
全てのデバイスが同期的に動作する必要があるため、あるデバイスが他のデバイスよりも計算が遅い場合(例えば、一部のGPUが他のGPUよりも負荷が高い場合)、他のデバイスはその遅いデバイスが終わるまで待つ必要があります。これにより、デバイスのリソースが効率的に使用されないことがあります。
(3) メモリの制約
各デバイスでモデルのコピーが必要なため、モデル自体が大きすぎる場合は、それぞれのデバイスでモデルを保持するのが難しくなることがあります。この場合、データ並列よりもモデル並列の方が適している場合があります。
5. データ並列の実装方法
データ並列は、主要なディープラーニングフレームワーク(TensorFlow、PyTorchなど)でサポートされています。これらのフレームワークでは、ユーザーが簡単にデータ並列を実装できる仕組みが用意されています。
(1) PyTorchでのデータ並列
PyTorchでは、DataParallel クラスや DistributedDataParallel クラスを使用して簡単にデータ並列を実装できます。
import torch
import torch.nn as nn
import torch.optim as optim
# モデルの定義
model = MyModel()
# データ並列の設定
model = nn.DataParallel(model)
# GPUに転送
model = model.cuda()
# オプティマイザの設定
optimizer = optim.Adam(model.parameters())
# 訓練ループ
for data, target in train_loader:
data, target = data.cuda(), target.cuda()
optimizer.zero_grad()
output = model(data)
loss = loss_fn(output, target)
loss.backward()
optimizer.step()
このコードでは、DataParallel がモデルの複製とデータの分割、計算結果の集約を自動的に行ってくれます。
(2) TensorFlowでのデータ並列
TensorFlowでは、tf.distribute.MirroredStrategy を使用してデータ並列を実装します。
import tensorflow as tf
# データ並列の設定
strategy = tf.distribute.MirroredStrategy()
with strategy.scope():
# モデルの定義
model = MyModel()
# オプティマイザの設定
optimizer = tf.keras.optimizers.Adam()
# モデルのコンパイル
model.compile(optimizer=optimizer, loss='sparse_categorical_crossentropy')
# 訓練
model.fit(train_dataset)
このコードでは、MirroredStrategy を使用することで、自動的にデータ並列が行われます。
6. データ並列の実例
データ並列は、以下のようなシナリオで特に効果的です。
-
画像認識: 例えば、大規模な画像データセット(ImageNetなど)を使って、ResNetなどのディープニューラルネットワークを訓練する際に、データ並列を使用して複数のGPUで並列に計算することで訓練速度を大幅に向上させることができます。
-
自然言語処理(NLP): BERTやGPTなどの大規模なトランスフォーマーモデルを訓練する際に、データを分割して複数のGPUで処理することで、効率的に訓練を行うことが可能です。
まとめ
データ並列は、複数のデバイスで同じモデルを動作させ、異なるデータバッチに対して並行して計算を行う手法です。これにより、訓練速度の向上や大規模データセットの効率的な処理が可能になりますが、通信オーバーヘッドや同期の問題などが課題となることもあります。
SimpleRNN Language Model
シンプルなRNNを用いた言語モデルは通常以下のような構成になる。TimeAffineレイヤに関しては処理を高速化するためにAffineレイヤを実装せずにTimeAffineレイヤの中で全ての時刻ステップのアフィン変換を1回の行列演算で実現している。

WaveNet
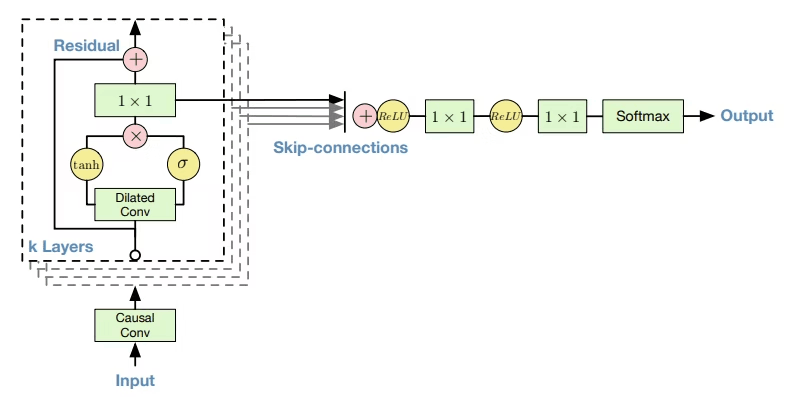
PixelCNNアーキテクチャに基づく音声生成モデル。
音声波形のデータ集合
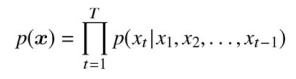
以上式は各音声サンプル
が x_t より前の全ての時刻ステップにおける音声サンプルに依存して決定されることを表している。 t
ダイレイト・コーザル畳み込み(dilated causal convolution)
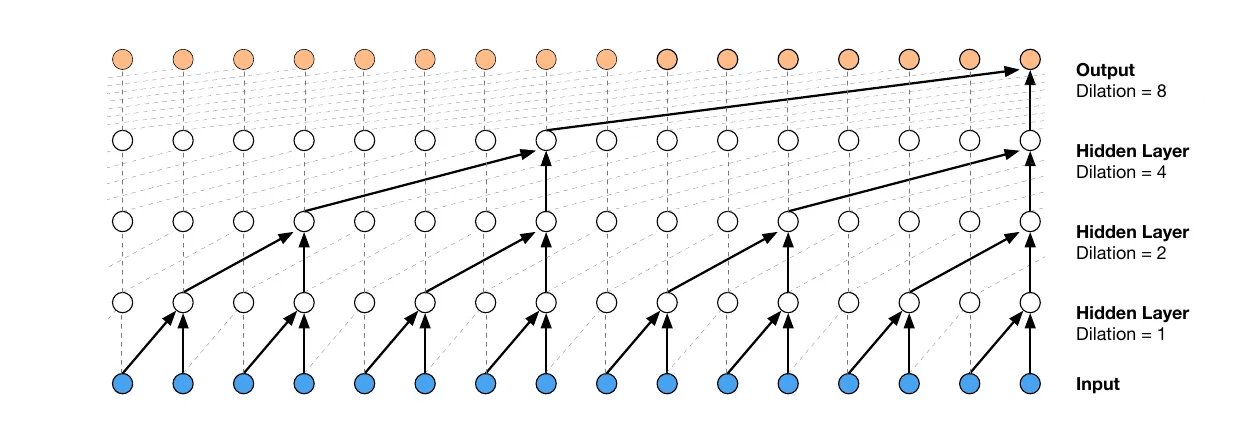
WaveNetでは,コーザル畳み込みとダイレイト畳み込みを組み合わせたダイレイト・コーザル畳み込みを用いる。これにより,以下メリットを享受した畳み込みを行うことができる。
- 時間的因果関係を保ちながら畳み込める
- カーネルサイズや層数を増やすことによるパラメータ数の増加を防ぐ
- シーケンスデータの長期依存性を得るための広い受容野が確保できる
コーザル畳み込み(causal convolutions)
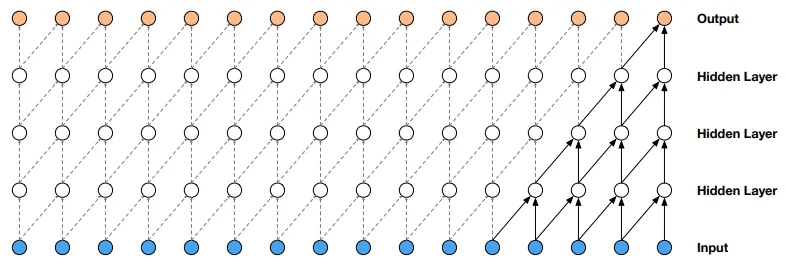
カーネルが入力データの現在の値だけでなく,その過去のデータのみから畳み込みを行うようにカーネルを設計する。これにより,時間順序を破らずに因果関係を考慮できる。
この畳み込みの利点は再帰接続がないためRNNに比べて計算が高速(並列演算可能)
また,コーザル畳み込みと同等な手法としてマスク畳み込みがある。マスク畳み込みはマスクテンソルと畳み込みフィルタを成分ごとに掛け算してから畳み込みを適用する手法である。
Transformer
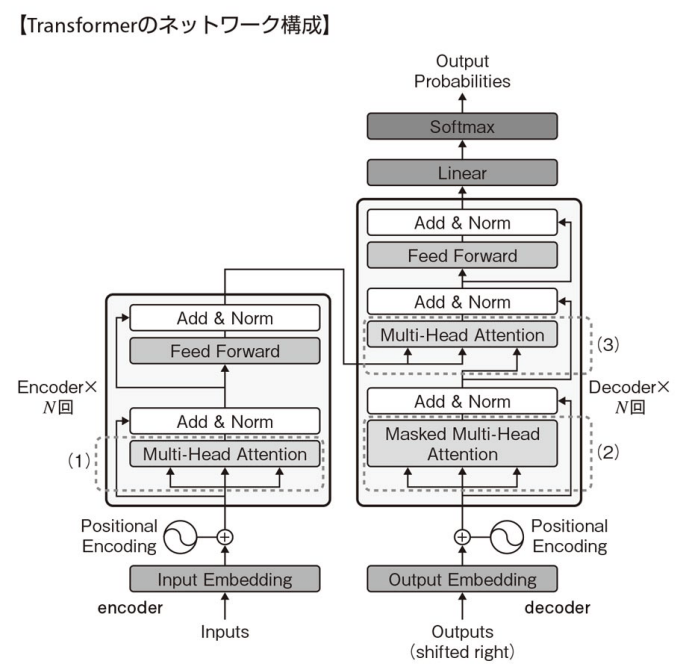
RNNを使わずアテンションのみで系列データを扱える。再帰結合がないため計算効率が高く,翻訳タスクにおいて当時最高性能を達成していた。
- 図の左側の四角枠がエンコーダであり,N回繰り返される(N層ある)。
- 1つのエンコーダはMulti-Head AttentionとFeed Forward Networkで構成される。Feed Forward Networkでは同じパラメータを用いた全結合の計算が各単語位置に適用される(同じ重みをもつFFNが全単語に対して個別に適用される)。
- 図の右側がデコーダであり,これもN回繰り返される(N層ある)。
- 1つのデコーダは,マスク付きのMulti-Head Attention,Multi-Head Attention,Feed Forward Networkで構成されている。
- エンコーダのMulti-Head Attentionにおいて,query,key,valueは全て直前のエンコーダ出力(Input EmbeddingしてPosityonal Encodingした後の値)から伝わってくる。
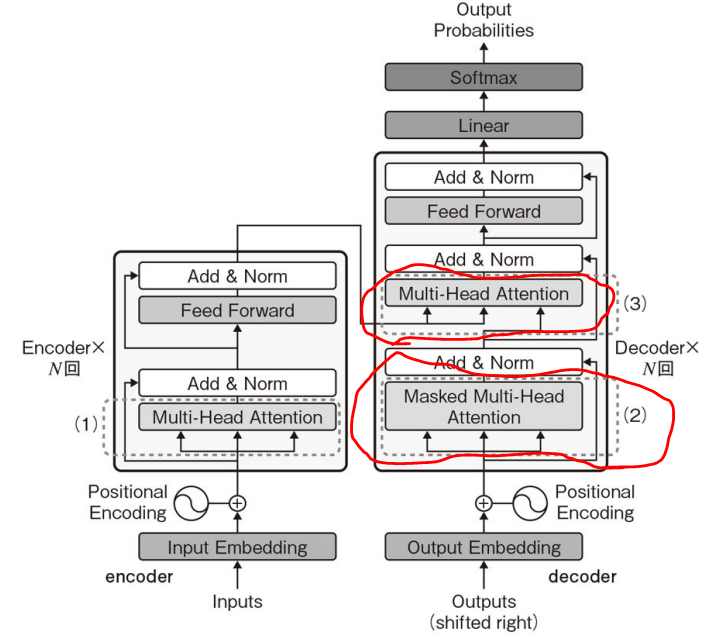
デコーダにおけるMulti-Head Attentionは2種類ある。
- デコーダの入力に近いMulti-Head Attention((2)の箇所)はSelf-Attention(
Q K -∞
良記事: https://zenn.dev/yamada_quantum/articles/6264faed5ff1f4
- デコーダの入力から遠いMulti-Head Attention((3)の箇所)はエンコーダの出力に基づいてデコーダがアテンションを行う部分。エンコーダでは入力されたシーケンス全体のコンテキスト情報が計算されているため,この情報を用いることでデコーダは次のトークンを生成する際に元の入力情報を参照することができる。
大まかな処理の流れ:
- query生成: デコーダの出力ベクトル(Masked Multi-Head Attentionからの出力)をもとに、queryが生成されます。
-
エンコーダの出力を参照: エンコーダの出力が、エンコーダ-デコーダアテンションにおいて、keyとvalueとして使用されます。
- key: エンコーダの出力に基づいて計算され、デコーダのqueryとの関連性(アテンションスコア)を計算します。
- value: アテンションスコアに基づいて、エンコーダからの出力を集約し、デコーダに返すべき最適なコンテキスト情報を計算します。
- アテンション計算: デコーダのqueryが、エンコーダのkeyとアテンションスコアを計算し、その結果に基づいてvalueを加重平均して次の層に渡します。
ポジショナル・エンコーディング
TransformerはRNNのような再帰的な処理やWaveNetのような畳み込みが存在しないため,ポジショナル・エンコーディングにより系列順序に関する情報を考慮できるようにする。
ポジショナル・エンコーディングは単語の順序に関する情報が埋め込まれたベクトルであり,単語埋め込みベクトルに加算される。

-
- 特に学習可能なパラメータはなく,サイン関数とコサイン関数により単語位置を表現する。
- ベクトルの各要素はサイン関数とコサイン関数を用いて異なる周波数で変化する。これにより,モデルは位置情報を効果的に捉えることができる。(以下あるposにおけるポジショナル・エンコーディングベクトル)
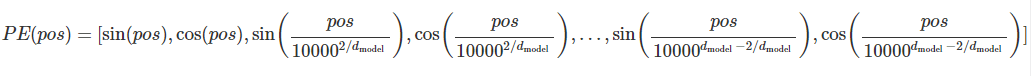
モデルの比較指標(計算複雑性 etc.)
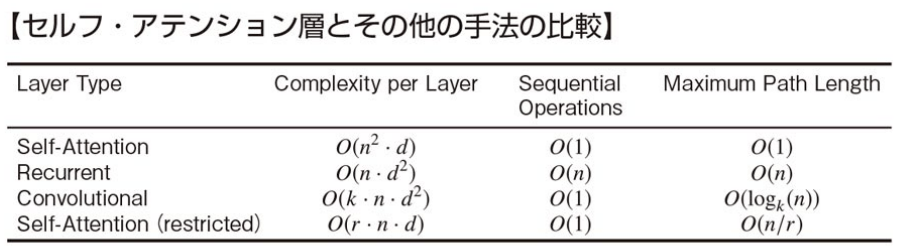

Complexity per Layer: 1層あたりの合計の計算複雑性
- 通常は
d>n
Sequential Operations: 系列を処理する最小の操作回数
- Sequential Operationsが少ないほど並列化しやすい。なぜなら,シーケンシャルな処理だと各操作が前の操作を完了するまでに待機する必要があるため,この回数が少ない方が並列化しやすい
Maximum Path Length: 入力位置と出力位置を結ぶパスの最大経路長
- Maximum Path Lengthが短いほど長距離依存性を学習しやすい。Maximum Path Lengthは、モデル内で情報が入力から出力に伝達される際の最も長い経路のことを指す。パスが短いほど、情報が効率的に伝わりやすく、特に長距離依存性(例えば、文中の遠く離れた単語同士の関係)を学習しやすくなる。
BERT
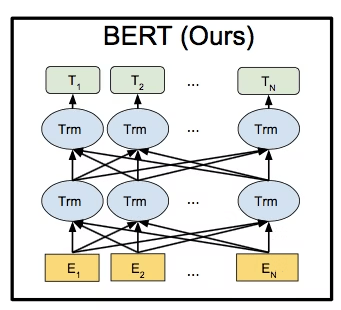 BERTは自然言語処理用のモデルである。
BERTは自然言語処理用のモデルである。
- BERTの内部には,Transformerのエンコーダが用いられている。図中のTrmはTransformerのエンコーダレイヤ(Multi-Head AttentionとFeed Forward Network)を表している。
- BERTは双方向なモデルであるという特徴がある。これはTransformerのエンコーダを用いて過去の単語も将来の単語も使って[MASK]の単語を予測するため(※以前のモデルは過去の単語だけを使って将来の単語を予測している形であった)。
- あらゆるNLPタスクにファインチューニング可能。

- BERTは事前学習と再学習の2段階で学習を行う。BERTは事前学習が肝。
- 事前学習は教師なし学習,再学習は解きたいタスクに合わせて教師あり学習をおこなう。
- 再学習はタスクに合わせて入力するだけ。
C T_i

- 事前学習に精度向上のポイントがあり,事前学習として"Masked Language Model:複数個所が穴になっている文章の単語予測"と"Next Sentence Prediction:連続した文かどうかを予測する問題" の2つの問題を同時に解く。
- 入力は2つの文の単語列。単語列は必ず
[CLS] [SEP] [MASK]
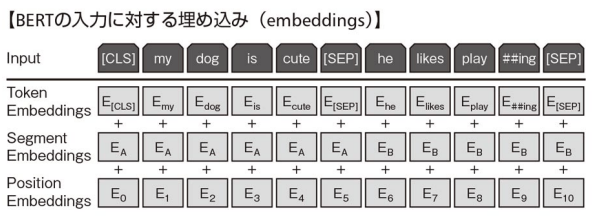
- BERTの入力に対する埋め込みは,入力された単語列を"トークン埋め込み","セグメント埋め込み","ポジション埋め込み"の和で表す形となる。
- トークン埋め込み: 単語の違いを表す情報
- セグメント埋め込み: 文の違いを表す情報
- ポジション埋め込み: 入力された単語の順序を表す情報
- 2文をくっつける時は,間に
[SEP]