🔰

モナド入門：プログラミング言語を横断する共通の特徴から学ぶ

に公開3件
Haskell
Scala
関数型プログラミング
PureScript
モナド
tech

はじめに

プログラミング言語におけるモナドを説明する記事の数は年々増えてきており

{世はまさに大モナド時代！}
といえるようないえないような状態です。
そういった中ではn番煎じになるかと思いますが、私もそのnの一つになろうかと思いこの記事を書きました。

誰向けの記事か？

モナドというキーワードを見かける或いは人から聞くが、聞いたり調べてもよくわからない。
一体何の役に立つというのか。
そう思っている方向けの記事です。

モナドがよくわからないのは何故か？

モナドの説明を人から聞いたとき、あるいは読んだとき、多くの人が「よくわからない」と口にします。
私もそうでした。

何故でしょうか？

当たり前のようなことをいいます。

それはモナドが抽象的な概念だからです。
　
抽象的な概念は、それを知らない人に向けて説明するのが難しいですし、説明された人が理解するのも難しいものです。

更に付け加えるならば、次のような理由もあるでしょう。

  • 馴染みのない言葉が使われる
  • 一定の前提知識が要求される
    • モナド自体の前提知識
    • モナドの説明に用いるプログラミング言語の知識

例えばよくあることとして、モナドが説明される前に関手(Functor)が説明されるケースがあるかと思いますが、使ったことのない言語で「まず関手というのがあって」と始められたら、いきなりモナドを知りたい方にとってはモチベーション的に厳しいのではないでしょうか。
(最初から順を追って基礎からステップバイステップで理解していきたい、というなら別)

そこを踏まえ、この記事では具体から抽象へのボトムアップなアプローチで、かつ用いるプログラミング言語の言語仕様やモナドの前提知識を要求せずに説明してみます。

とはいえ前提を無視するわけにもいかないので、そちらは読者が知りたそうなことを説明した後、最後に補足として簡単に説明します(興味があったら各自深堀っていただけたらと思います)。

あなたが知りたいのは「何の」モナドですか？

モナドとは何なのか、という問いについて私なりに説明する前に、一つ質問があります。
そもそも、あなたが知りたいのは「何の」モナドですか？
「え？何のって何？」
とか

と思ったでしょうか。

はっきりしていないなら、そこから整理しましょう。
はっきりしているなら先に飛んでもらって構いません。

情報整理

プログラミング言語におけるモナドは、数学の一分野である圏論のモナドが源流にあり、そこからプログラミングへの応用が考えられ、実際のプログラミング言語に落とし込まれてきたという歴史があります。

つまり一口にモナドについて理解しようとといっても

  1. 圏論のモナド
  2. プログラミング言語における一般的な概念としてのモナド
  3. 各種プログラミング言語で定義および実装されているモナド

といった切り口があるわけです。

下に行くに従って具体的になっています。

更にそれぞれについて

  • 定義
  • 使い方
  • 何の役にたつのか

があります。

あなたが本当に知りたかったモナドは、上記のどこにあたるのか整理できましたでしょうか。

モナドについて調べるとこのあたりが渾然一体となって説明されるケースがあるため※、こういった全体像および自分はどこにフォーカスしたいかを意識していないと容易に沼にハマったり道に迷います。
※すみません。かくいう私もそういう記事を書いています。

だから先にこの話をしたかったのです。

この記事ではどのモナドをどう説明するか

この記事では、2(プログラミング言語における一般的な概念としてのモナド)と3(各種プログラミング言語で定義および実装されているモナド)を説明します。

説明の順序としては、具象->抽象の順で進めます。
具体的なプログラミング言語をいくつかピックアップし、言語が異なってもモナドとしての特徴は共通しているということを見ていくことで、抽象的な理解を目指します。

この記事で説明しないこと

定義や、抽象的にどう役立つかの説明はしますが、使い方・実用例などについては一切説明しません。

ということで、始めます！

モナドを特徴から理解する

モナドとは何なのかを理解するにあたって、必要だと私が思うのが、モナドをモナドたらしめている特徴を知るということです。

モナドがこのように広く普及しているということは、なんらかの有用性があるはずで、それはモナドのもつ特徴に依るものだと考えられるからです。

ではモナドとはどういう特徴をもったものなのでしょうか？
また、何ができればモナドと呼べるのでしょうか？

このことを理解するには定義を見るのが一番です。

そう、凄く重要なことなのですが、モナドには定義が存在するのです。
しかも数学的な背景を持つ定義です※。
少なくとも定義についてであれば、異論の余地なくモナドを説明できます。
※ちなみに数学的な背景については別の記事で見ていきます。

モナドの定義

では言語ごとのモナドの定義を、実際のソースコードで見ていきましょう。
言語としては、Haskell/PureScript/Scalaを用います。
なぜならば、これらの言語はモナドが明確にモナドとして抽象的に定義されているからです。
そのおかげで「○○は実質的にモナドといえます」みたいな表現を使わずダイレクトにモナドの話ができます。

【前置き】

  • モナドにまつわる関数を抽象的に捉えるため定義部分のみにフォーカスします。
    • したがって私が載せるコードからは、コメントや一部の実装部分を削除しています。
    • 適宜元のソースコードへのリンクを記載していきますので、全体を見たい方はそちらをご確認ください。
  • 各言語のコードは読めなくても大丈夫です！

Haskellのモナド

Haskellではモナドは型クラスMonadとして定義されています。

class Applicative m => Monad m where
  (>>=) :: forall a b. m a -> (a -> m b) -> m b
  return :: a -> m a

冒頭で伝えたように言語仕様の知識は不要です。
こんな感じに視覚的に理解しておければよいです。
正直returnってのはなんかaってのがm aってのに変わってるんだなくらいでOKです。

引数を分けて、同じ要素(aとかbとか)を同じ色にした図

定義の話に戻りましょう。
どうやらHaskellでは、>>=とreturnがモナドを特徴づけているようです。

全体を見たい方はこちらをどうぞ。

PureScriptのモナド

PureScriptでもモナドは型クラスMonadとして定義されています。
より正確には型クラスApplicativeとBindを継承する型クラスとして定義されています。

class (Applicative m, Bind m) <= Monad m

class Apply m <= Bind m where
  bind :: forall a b. m a -> (a -> m b) -> m b

infixl 1 bind as >>=

class Apply f <= Applicative f where
  pure :: forall a. a -> f a


PureScriptではbindとpureがモナドを特徴づけているようです。
見やすく一つにまとめて記載しましたが、実際は別々のモジュール Monad.purs, Bind.purs, Applicative.purs に分かれています。

Scalaのモナド

Scalaではcatsやscalazというライブラリにモナドが定義されているようです。
今回はcatsでの定義を見てみるのですが、こちらはトレイトとしてモナドが定義されています。
Monadには、FlatMapやApplicativeといったトレイトがミックスインされています。

trait Monad[F[_]] extends FlatMap[F] with Applicative[F] {
}

trait Applicative[F[_]] extends Apply[F] with InvariantMonoidal[F] { self =>
  def pure[A](x: A): F[A]
}

trait FlatMap[F[_]] extends Apply[F] with FlatMapArityFunctions[F] {
  def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
}


ScalaではpureとflatMapがモナドを特徴づけていますね。
他にも色々メソッドが定義されていますが本質的に重要なのはこの二つなため省略しています。
ソースコードは、Monad.scala, Applicative.scala, FlatMap.scalaになります。

比べてみよう

よく比べてみると似たような定義であったり名前の関数やメソッドが定義されているようです。
せっかくなので、これらをまとめて比べてみましょう。

なんと！名前こそちょっとずつ異なれど、視覚化した関数の形は完全に一致しています！（わざとらしいな）。
どうやらこの3つの言語のモナドは同じ関数によって特徴づけられているようですね。

コードで比べた場合
言語 定義
Haskell return :: a -> m a
PureScript pure :: forall a. a -> f a
Scala pure[A](x: A): F[A]
言語 定義
Haskell (>>=) :: forall a b. m a -> (a -> m b) -> m b
PureScript bind :: forall a b. m a -> (a -> m b) -> m b
Scala flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]

更に比較しやすくするため次のルールで表記を揃えてみます。

  • returnとpureはpureに統一する
  • >>=、bind、flatMapはbindに統一する
  • HaskellやPureScriptからforallは除く
  • Scalaの記法をHaskell/PureScriptと合わせる

するとこのようにまったく同じ形になります。

言語 pureの定義 bindの定義
Haskell a -> m a m a -> (a -> m b) -> m b
PureScript a -> f a m a -> (a -> m b) -> m b
Scala a -> f a f a -> (a -> f b) -> f b

実は他のプログラミング言語でも、モナド（とみなせるもの）は同じ意味合いの関数を持っています。

ということで、具体的なプログラミング言語におけるモナドの定義は概ね理解できたでしょう。

では続いてこれらの関数ってなんなん？という説明をしていくのですが、その前にこの記事で今後使う名前とコード上の記法を統一しておきたいです。

>>=,bind,flatMapは代表としてbindという名前を選びます。
return,pureは代表としてpureという名前を選びます。
関数定義の記法としては引数を->で区切るHaskell/PureScriptの記法を用います。
(この記事用に別の記法を考えてもよかったのですが、->は次回の記事まで含めて考えるとわかりやすいなと思い、->を使うことにしました)

ということでやっていきましょう。

pureとかbindってなんなの？

その前に

->を使った関数定義の説明を少し加えておきます。
a -> bとはa型をb型に写すという意味になります。
で、丸括弧で囲まれた部分は、それ自体が関数という扱いになります。
だからa -> (b -> c) -> cとはa型と「b型をc型に写す関数」をc型に写すという意味になります。

Haskell/PureScriptにおける ->

->は型をもとに新たな型を作る型コンストラクタと呼ばれるものの一つです。
これは関数の型を作る型コンストラクタですね。

ghci> :k (->)
(->) :: * -> * -> *

ghci> :k (->) String
(->) String :: * -> *

ghci> :k (->) String Bool
(->) String Bool :: *

> :k (->)
Type -> Type -> Type

m aとは？

bindやpureには、m aやm bといったaやbの隣にmがくっついたものが出てきました。
これを先に説明しておきます。

まずaやbですが、これは任意の型です。
(Haskell/PureScriptなどでは型変数と呼ばれます)
文字列型とか数値型とかブール型とか、任意の型を当てはめられるプレースホルダくらいの理解で大丈夫です。

続いてmです。
これも任意の型なのですが、モナドにおいてのmは「計算の概念」「計算効果」「文脈」など様々な表現で説明されるものです。
この記事では「計算の文脈」あるいは単に「文脈」などと表現することにします。

mは計算の文脈であり、aはその文脈をもった計算の結果。

です。
つまりm aとはmという文脈を伴ったaの型ということです。

私がこれまで使ってきた図でmとaを横にくっつけて並べて描いてきたのは、これを表現するためでした。
（mがaを包んでいる（含んでいる）みたいに見えてしまわないようにしたかった）

些細な違いだけど・・・・・・

大分抽象的な話をしてきたので、ここら辺でmやaに具体を当てはめてみようと思います。

いくつか例を挙げるとこんな感じでしょうか。
どういう文脈でのどういう結果や値なのかもあわせて書いてあります。

なんとなくイメージはできたでしょうか？
できたと信じて、pureとbindの説明に入っていきます。

pureとは？

さて、すぐ上で説明したとおり m a とは文脈を伴った型でした。
とすると、pure: a -> m aとは、型aを文脈mを伴った別の型m aに写す関数といえます。

これがあれば任意の型に文脈を持たせられるよ、ってことですね！
やけに単純ですが、こんなもんです。
どんどんいきましょう。次はbindです。

bindとは

bindはm a -> (a -> m b) -> m bというように引数としてはm aとa -> m bの二つが登場します。

まず1番目の引数のm aは前述のとおり文脈を伴った型です。
そして2番目の引数の関数の戻り値のm bや、bindの戻り値のm bも同じく文脈を伴った型です。
この二つは同じ文脈を伴っています。

bindでは文脈は保たれるということですね。

次に(a -> m b)という関数の引数aを見ると文脈が剥がされています。
しかしこの関数が返す型は文脈を伴った型です。

aとbに適当に型を当てはめてみるとbindはこんな感じの意味合いになるでしょうか。

bindとmapの違い

bindみたいな形をした関数をどこかでみたことがないでしょうか。
・・・・・・
そう、map関数です。
大体どのプログラミング言語にも用意されてるやつです。

このmap関数とbindの異なるところに着目すると、bindの特徴がより鮮明に見えてくるのではないでしょうか。

ということでmapと比べてみましょう。
mapは(a -> b) -> f a -> f bと定義されますが、比べやすいようにちょいと引数の順序を入れ替えて比べてみます(引数の順序はこの説明においては重要ではない)。

-- f は m に置き換えています
bind: m a -> (a -> m b) -> m b
map:  m a -> (a -> b)   -> m b

どちらも第一引数と、戻り値の構造は変わっていません。
違いは、第二引数の関数が返す型が文脈を伴っているか否か、ですね。
ということは、bindにおいてはそこが重要なわけです(じゃなければmapで事足りるわけなので)。

bindを使うと何が嬉しいか

bindはmapとは異なり、型aをbに写しつつ、bに文脈を伴わせることができます。

これの何が嬉しいのか、というと

  • bに文脈を伴わせることができること自体
  • 関数の定義によりそれが規定されている

ということです。

例えばmを上述した「値があるかもしれないし、ないかもしれない」型とし、aを文字列型とします。
この文字列型の値を数値型に変換したいとします。
このとき文字列型は必ずしも数値型に変換できるとは限らないため、「値があるかもしれないし、ないかもしれない」という文脈は引き継ぎたいです。
変換できたら値がある、変換できなかったら値はない、ということにしたいのです。

なんかmapでやれそうな内容ですよね？
実際できることなので、ためしにどうなるかやってみましょう。
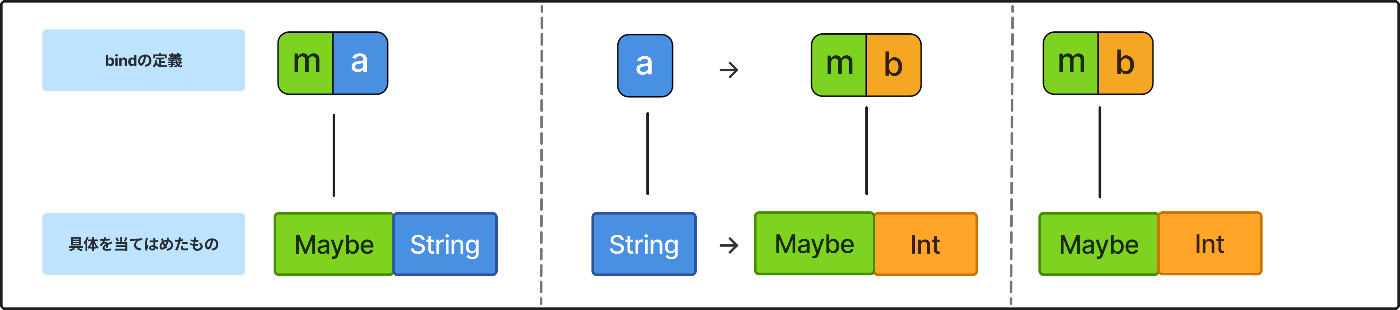
日本語の文章で書いていくと表現が冗長になるので、「値があるかもしれないし、ないかもしれない」型はMaybe、文字列型はString、数値型はIntとします。

map: m a -> (a -> b) -> m bの
mをMaybe
aをString
bをMaybe String※
として置き換えてみます。
※文脈を引き継ぐため、第二引数の関数は文脈を伴う型を返したい

すると、この場合のmapはMaybe String -> (String -> Maybe Int) -> Maybe (Maybe Int)のようになります。
文字だとわかりづらいかもなので図で見てみましょうか。

なんと戻り値のMaybeが二重になってしまいました・・・・・・。

これは使いづらい。中の値にアクセスするためには二回Maybeを剥がす必要があります。

使う例(ひどいコード)
let result = Maybe (Maybe Int)を返す関数
case result of
  Just innerResult -> case innerResult of
      Just value -> value
      Nothing -> -1
  Nothing -> -1

こんなことは毎回やってられません。

一方bindでは、a -> m bというように文脈を伴うbが期待されているため、このようなネスト状態になることは基本的にありません。

なので、こういう場合はmapよりbindの方が的確だといえます。

更に嬉しいのは、1つ目の引数とbindが返す結果の型がどちらも文脈mを伴うため、(a -> m b)のような関数をどんどん結合していけるということです。
bindにはしばしば中置演算子版の>>=も定義されている(Haskellはむしろこっちが定義されている)ため

f: (a -> m b)
g: (b -> m c)

という関数があるとき
x >>= f >>= g
と結合できるわけです！

これはHaskellのdo記法ではこう書くことができます。
手続き的な処理に見えますが、実際は(a -> m b)という関数が結合されているわけです。

execute = do
  x <- xを返す関数
  y <- f x
  g y

このように書けるのはbindのおかげ、というわけです。

まとめ

私達が普段扱っているプログラムというのは概ね副作用がある世界で動作していると思いますが、それはつまり処理の入口から副作用という文脈を伴った計算をしているといえるのではないでしょうか。
(Haskellはメイン関数はIO ()を返しますし、PureScriptではEffect Unitを返す、というようになっています)

ということは副作用を伴うプログラムというものは、(a -> m b)的な関数の合成で構成することができるといえ、その中でbindが中心的な役割を果たしているわけです。

だから十分bindひいてはモナドは役に立っているわけなんですね。
じゃあpureは？
pureはbをm bにするとき必要じゃないですか！

ということで、プログラミング言語におけるモナドには、bindやpureといった関数が定義されており、モナドはこれらの関数によって文脈を伴う計算において中心的な役割を果たしているということがわかりました。

補足

最後にいくつか補足を加えておきます。
それは、Functorとモナド則です。
Functorは実コードでも登場するもので、モナド則は登場しません。
どちらもモナドであることの前提なのですが、プログラミング言語においてのモナドの有用性を示す上でこちらを先に説明するのは、徒に認知不可を高める恐れがあると判断したため、最後にもってきたのでした。

これから定義などを説明しますが、関心がなければここで読むのを止めていただいても大丈夫です。

Functor

これはめっちゃ簡単で、bindの話でも出てきたmap関数が定義されたやつです。
ここについては丁寧に説明するつもりはありません（すみません）。
とはいえ各言語のFunctorを見ていくくらいはしましょう。

Haskell

Haskellのモナドのコードを読んだとき、飛ばしましたが、Haskellのモナドのクラス階層は次のように
Functor => Applicative => Monadとなっています。

class Applicative m => Monad m where
    (>>=) :: forall a b. m a -> (a -> m b) -> m b
    return :: a -> m a
    return = pure

class Functor f => Applicative f where
    pure :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b

class Functor f where
    fmap :: (a -> b) -> f a -> f b

つまりHaskellのモナドは前提としてApplicativeとFunctorでもあります。
が、今回はFunctorのみに着目します。
理由は記事の都合です。
次回の記事で圏論との繋がりを見ていくつもりなのですが、実は圏論のモナドの定義にはFunctorに対応するものはあれど、Applicativeに対応するものは存在しないため、記事の趣旨から外れるためです。

HaskellではFunctorのmap関数はfmapという名前になっていますね。

PureScript

まず省略していたPureScriptのモナドのクラス階層をみてみるとこのように
Functor => Apply => Apply, Bind => Monadとなっています。

class (Applicative m, Bind m) <= Monad m

class Apply f <= Applicative f where
  pure :: forall a. a -> f a

class Apply m <= Bind m where
  bind :: forall a b. m a -> (a -> m b) -> m b

class Functor f <= Apply f where
  apply :: forall a b. f (a -> b) -> f a -> f b

infixl 4 apply as <*>

class Functor f where
  map :: forall a b. (a -> b) -> f a -> f b

後発の言語だけあってHaskellより整理されている印象です。
HaskellではApplicativeに定義されていた<*>がPureScriptではApplyに定義されています。
そしてmap関数はそのまんまmapという名前で定義されています。

Scala

Scalaのcatsでは次のようにクラス階層は本筋のtraitだけ取り出すと
Functor => Apply => Applicative, FlatMap => Monad
となっています。

trait Monad[F[_]] extends FlatMap[F] with Applicative[F] {
}

trait Applicative[F[_]] extends Apply[F] with InvariantMonoidal[F] { self =>
  def pure[A](x: A): F[A]
}

trait FlatMap[F[_]] extends Apply[F] with FlatMapArityFunctions[F] {
  def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
}

trait Apply[F[_]] extends Functor[F] with InvariantSemigroupal[F] with ApplyArityFunctions[F] { self =>
  def ap[A, B](ff: F[A => B])(fa: F[A]): F[B]
}

trait Functor[F[_]] extends Invariant[F] { self =>
  def map[A, B](fa: F[A])(f: A => B): F[B]
}

クラス階層としてはPureScriptと似ていますね。
そしてmap関数はまんまmapという名前で定義されています。

まとめ

各言語のモナドの定義を上位階層まで見ていくとFunctorがあり、これまたどの言語も同じ意味合いの関数が定義されていました。

いわゆるmap関数がどのような意味でどのように役立つかはあらためて説明するまでもないと思いますが、なぜモナドがFunctorでもあることを前提としてるのかは釈然としないかもしれませんね。

これは元ネタである圏論のモナドにおいて、関手(Functor)が前提にあるからです。
このあたりは冒頭の方に載せた圏論とのつながりを書いた記事を読んでいただけるとわかるかもです。

モナド則

これまで見てみたHaskell/PureScript/Scalaといったプログラミング言語のモナドでは、モナドとして満たすべき条件 モナド則 というものがあります。

モナド則を知らなくても各プログラミング言語のモナドは理解できますし、既存のモナドを使う上では（モナド則を満たすように作られているはずなので）困らないはずですが、モナドとはpureやbindが定義されている上で、モナド則を満たさないとならないものなので、書いておきます。

  • 左単位律: pure a >>= f == f a
  • 右単位律: m >>= pure == m
  • 結合律: (m >>= g) >>= h == m >>= (\x -> g x >>= h)

ここはざっくり書きましたが、もっと詳しく知りたい人向けにこちらに詳しく書いていますので、よければ御覧ください。
https://zenn.dev/funnycat/articles/d92e16dfc59a49

おわりに

複数の具体的なプログラミング言語のモナドの定義を見比べることで、モナドを特徴づける関数が同じ構造をしていることを見てきました。

また、これらの関数の特徴を踏まえ、モナドがどのように役立つのかも見てきました。

今回このようなアプローチをとって説明をしてきたわけですが、少しは理解のお役に立てましたでしょうか？

そうであることを祈りつつ、この記事を終わりにさせていただきたいと思います。

Discussion

colacola

記事を書いて下さりありがとうございます。
モナドが理解出来ていないので質問させてください。

記事にあるように
bをMaybe String
とした場合
bindのところの画像の真ん中は
String -> Maybe Maybe String
となってしまうのではないかと思ってしまうのですがなぜ入れ子になってしまわないのかが理解できていません。
もし回答頂けましたら嬉しいです。

funnycatfunnycat

colaさん
記事を読んでいただきまして、ありがとうございます。

ご質問いただいた内容について、回答いたします。

冗長になってしまうことをご容赦いただきたいのですが、質問いただいた節について、あらためて説明してみます。

まず『bindを使うと何が嬉しいか』の節では次のような前提で話を進めています。

  • m a の a の型を変換したい
    (この例ではMaybe StringのStringをIntに変換したい)
  • 変換の際、mという文脈は保ちたい
    (この例ではMaybeの文脈を保ちたい)

そしてこういった変換が行えそうな関数としてmapやbindがあることを紹介しています。

  • mapではa -> bという型の関数を受け取る
  • bindではa -> m bという型の関数を受け取る

この前提のもと、それぞれの変換の関数で、Maybe Intを返したらどうなるかを考えています。
ここについて上記の前提を踏まえつつ、aやbなどを少しずつ置換しながら今一度説明してみます。

まずmapはm a -> (a -> b) -> m bという型の関数です(引数の順序は入れ替えてますが)。

  1. まずmをMaybeで置き換えます。
    Maybe a -> (a -> b) -> Maybe b
  2. 次にaをStringに置き換えます。
    Maybe String -> (String -> b) -> Maybe b
  3. 変換の関数ではMaybe Intを返したいという前提があるので、最後にbをMaybe Intに置き換えます。
    Maybe String -> (String -> Maybe Int) -> Maybe (Maybe Int)

同じことをbindについても行ってみます。
bindはm a -> (a -> m b) -> m bという型の関数です。

  1. まずmをMaybeで置き換えます。
    Maybe a -> (a -> Maybe b) -> Maybe b
  2. 次にaをStringに置き換えます。
    Maybe String -> (String -> Maybe b) -> Maybe b
  3. 変換の関数ではMaybe Intを返したいという前提があるので、最後にbをMaybe Intに置き換えます。
    Maybe String -> (String -> Maybe Int) -> Maybe Int

さて、ここであらためて質問を読み返しながら回答を書いてみます。

記事にあるように bをMaybe String とした場合

ここについては、前提として変換の関数で返したいのはMaybe Intなのですが、
bindの場合、変換の関数で返す型はm bなので、bそのものをMaybe Intに置き換えずとも、m bを返すことになっているので、やりたいことが素直に実現できます。

ですので

なぜ入れ子になってしまわないのか

については、やりたいことを実現するにあたって、入れ子にする必要がない、というのが回答になります。

以上、あらためて説明してみましたが、ご質問に対してお答えできていたら幸いです。

たけぴょんたけぴょん

何度もHaskellのモナド(とApplicative)に挫折していましたが、この記事の文脈という表現が自分の中でイメージがマッチして理解が深まったような気がします。とても助かりました。

少々記事内容から飛んでしまうのですが質問させてください。
圏論の文脈ではモナドはCを圏として関手T:C \rightarrow Cと2つの自然変換\eta : 1_C \rightarrow Tと\mu : T^2 \rightarrow T .... と定義されています（Wikipediaの定義を引用）が、Haskellでのreturnが自然変換\eta : 1_C \rightarrow T、>>=が自然変換\mu : T^2 \rightarrow Tに対応するのでしょうか？
お手隙あればご回答いただけると助かります。