モナド則を噛み砕く: 基本から学ぶその本質と重要性

はじめに

プログラミング言語におけるモナドについて調べたことがあるなら、まず間違いなく目にするであろう『モナド則』。

このモナド則について、私なりに説明を試みます。

その際、以下のことを心がけます。

• 行間は狭める
  簡潔さとのトレードオフですが、冗長になっても丁寧に説明します。
• わかりづらそうなところは図解する
• 圏論には触れない
  関係は大いにあるのですが、プログラミング言語のモナド則に集中します。

書いてみたらそれなりに長くなってしまったので、目次を見て「読まなくてもよさそうだ」と思ったら読みたいところまで飛ばしてください。

対象としている読者

この記事は次のような人を想定読者としています。

• モナドを調べててモナド則ってのが出てきたけどそもそも何なの？
• モナド則を表すコードを見たけどチンプンカンプン
• コードは読めるけど意味がわからないよ
• 意味の解説を読んだけどやっぱりわからない

この記事に書かれていること

この記事には次のようなことが書かれています。

• モナド則とは何なのか
• モナド則を満たさないとどうなるか

『モナド則とは何なのか』の話では、モナド則を構成する条件の名前や、その名前に込められた意味といった基本的なところから説明します。
これには認知不可を下げ段階的に理解を進める目的があります。

基本的な説明の後は、図により視覚的な補助をしつつコードの意味を説明していきます。
ここではモナド則につけられた名前とコードの内容の繋がりを知ることで、よりモナド則に親しんでもらい、記憶の定着につなげることを目指します。

『モナド則を満たさないとどうなるか』の話では、モナド則を満たさないモナドを具体的なコードで例示します。
モナド則を満たす必要がある、とはいうものの
「モナド則を満たさないからといって、それがどうだというのだ？」
という疑問に答えつつ、モナド則があることの有り難みを感じてもらいます。

説明しないこと

この記事では、説明においてプログラミングにおけるモナドに関わる二つの関数
pure, >>=(bind)
を多用しますが、これらの関数の説明は行いません。
ただ図解は行いますので、もしかしたら知らなくても雰囲気は掴めるかもしれません。

補足:
pureはreturnと呼ばれたり、bindはflatMapと呼ばれたりもしますが、この記事ではpureとbindに統一します。
また、bindとbindの中置演算子>>=は状況によって使い分けます。

この記事の例で用いるプログラミング言語

私の趣味でPureScriptを用いますが、この記事ではモナド則を満たさない例を除いて関数の実装にはほとんど言及しません。
それゆえ次の関数定義の文法さえ覚えていただけば、知らない人でも大体読めると思います。

関数定義

-- 【意味】
-- 関数名 :: 引数1 -> 引数2 -> 戻り値
function :: String -> String -> Int
function = 関数の実装

関数のシグニチャの定義は::の左側が関数名で、右側が->で区切られた引数と戻り値の型になっています。

定義の具体例ですが、pureやbindはこのように定義されます。
bindの(a -> m b)は関数の型です。

• pure :: a -> m a
• bind :: m a -> (a -> m b) -> m b

>>=はbindの中置演算子版で、左辺がm aで右辺が(a -> m b)になります。

---

ではここからモナド則の話をしていきます。

モナド則とは

詳しくは後ほど説明しますが、モナド則(Monad law) は次の3つの条件からなります。

1. 左単位律: pure a >>= f == f a
2. 右単位律: m >>= pure == m
3. 結合律:　 (m >>= g) >>= h == m >>= (\x -> g x >>= h)

モナド則はjoinという関数を使って書くこともできますが、この記事ではbindで書きます。

モナド則の条件の呼称

それぞれの条件には呼称があるのですが、日本語訳として一意には定まっていないようで、例えば左単位律は調べてみると左単位・左単位元・左単位法則・左同一性など様々な書かれ方をしていました。
数学における結合法則が結合律や結合則などと呼ばれているのと同じようなものですね。
この記事では○○律に統一することとします。

ちなみに英語だとHaskellWikiでは次のように書かれています。

1. Left Identity
2. Right Identity
3. Associativity

プログラミング言語においてのモナド則の立ち位置

前述の通りモナド則の各条件は具体的なプログラミング言語で書かれており、モナドはモナド則を満たしている必要があります。

しかし、プログラミング言語によってはモナド則を満たしていることをプログラムで証明することはできないのです。

もはやモナドが言語に組み込まれているといっても過言ではないHaskellやPureScriptなどの言語ですらできないのです。
厳密な証明が可能なのは定理証明支援系と呼ばれる言語(coq,Agda,Idris,Leanなど)だそうです※。
Haskell/PureScriptなどでできるのは証明ではなく、状況を限定した検証になるでしょう。

※筆者に知見がないため、詳しく説明はできません。

モナド則を満たすことの証明ができないとは

例えば左単位元律pure a >>= f == f aを満たすとはどういうことか。
まず、aとは「任意の」型の値を表しています。
任意とは「すべて」ということで、つまりこの世に存在し得るすべての型のすべての値に対して、この条件を満たすということなのです。

いわゆる単体テストを書いたことがある人は、上記の検証を実現することが不可能に近いことは容易に理解できるでしょう。
更にaは関数型である可能性もあるわけなのですが、多くの言語では関数型の比較自体ができないため、そういう意味でも難しいでしょう。

この制約をもっと緩くして、「aは文字列型の値」としてしまえば、部分的に検証が行えますが、これをもって証明したとは言えないでしょう。

なのでこれらのプログラミング言語では、「モナドはモナド則を満たすように定義すべし」となってはいますが、モナド則を満たすように定義したとしても、それを自動でチェックしてはくれないのです。

証明ができないからといって不安になる必要はない

あとから説明しますが、不安になる必要はありません。
大抵のケースではメジャーなライブラリが提供している既存のモナドを利用すれば事足りるでしょうし、そういったモナドはモナド則を満たすよう作られているはずです。
仮にモナド則を満たさないレベルの不具合があったとしたらとっくに修正されているでしょう。

また自分で独自のモナドを作る際は、モナド則が表す意味や、どうしたら条件を満たさなくなるか、などをきちんと理解できていれば「モナド則を満たしている」と自信を持つことができると思います。

モナド則、それぞれの意味

少し間が空いたため、モナド則を再掲します。

1. 左単位律: pure a >>= f == f a
2. 右単位律: m >>= pure == m
3. 結合律:　 (m >>= g) >>= h == m >>= (\x -> g x >>= h)

これから意味の解説を行っていきますが、まずは一般的な『単位律』や『結合律』の説明からはじめます。
『単位律』や『結合律』はモナド則特有のものではなく、様々な『単位律』や『結合律』が存在しており、上記の条件はあくまで『モナド則』における『単位律』『結合律』なのです。
そして様々な "律" の詳細は違えど表現したいことは同じなのです。

そのため予め『単位律』『結合律』とはこういうものだ、と認識をした上でモナド則の『単位律』『結合律』を見れば、より本質的な理解に結びつくと思います。

名前の意味がわかっていれば、条件の意味も理解しやすくなります。
そして一般的な『単位律』や『結合律』はモナド則のそれよりは理解がしやすいです。
そのため迂遠と思われるかもしれませんが、先にこれらの説明を行います。

逆にここをすっ飛ばして、いきなりpure a >>= f == f aという条件を「ドン！」と出して「このコードは⚪︎⚪︎なものと△△なものは等しいという意味です！」と説明した場合、わかるのはコードの意味であって、『左単位律』という名前との関係性や本質的な理解には結びつきづらいと思います。
（コードから全て察せる人はいると思いますが、少なくとも私は腹落ちできなかった）。
なので意外と『単位律』『結合律』という言葉の意味の理解は大事だと私は思うのです。

予備知識 - 単位律

単位律の説明には次の概念を用います。

• 集合と元
• 二項演算
• 単位元

したがって（すみませんが）、これらを理解しておく必要があります。
一歩ずついきましょう。

集合と元

『元』 とは、集合の『要素』のことです。
（馴染みがなければ頭の中で『要素』に置き換えてしまえばよいでしょう）
なので元といったときには前提として集合があるわけです。
この後出てくる単位元というのは元の頭に「単位」とついているわけだから、ただの元ではなく何か特別な元って感じがしますね。

集合と元のイメージ 元の数は有限かもしれないし無限かもしれない

二項演算

単位元は二項演算に対して定められるので、次は二項演算の説明をします。

ある集合${\footnotesize X}$があるとします。
この${\footnotesize X}$の任意の二つの元${\footnotesize a,b}$に対して定められる演算を二項演算といい、仮に二項演算を${\footnotesize \circ}$とするなら中置記法で${\footnotesize a \circ b}$のように書きます。
「任意の」というのは、「${\footnotesize X}$のすべての元に対して」ということです。
${\footnotesize \circ}$は例示のために適当に定めただけで、具体は文脈によって${\footnotesize f}$だったり${\footnotesize +}$だったり色々変わってきます。

二項演算のイメージ 実際はXのあらゆる元を適用できる

二項演算の結果が同じ集合の元になることを『集合${\footnotesize X}$は二項演算${\footnotesize \circ}$について閉じている』といいます。

閉じていない例

例えば自然数全体からなる集合${\footnotesize \mathbb{N}}$について二項演算「足し算」は閉じているといえます。なぜなら自然数からどの数を選んで足しあわせても結果は同じ自然数になるからです。

一方引き算に対しては閉じていません。
なぜなら例えば${\footnotesize 1 - 3}$としたとき、結果は負の数${\footnotesize -2}$になってしまい、これはもう自然数ではないからです。

ちなみに上で見たような集合と二項演算の組を代数的構造や代数系などと呼びます。

単位元・単位律

さて、やっと単位元の話ができます。
単位元とは、任意の元${\footnotesize a \in X}$に対して二項演算${\footnotesize \circ}$を行ったとき

$${\footnotesize a \circ e = e\circ a = a}$$

を成り立たせる元${\footnotesize e}$のことです。
つまり二項演算を行っても何も変えない、何も影響を与えない元のことです。

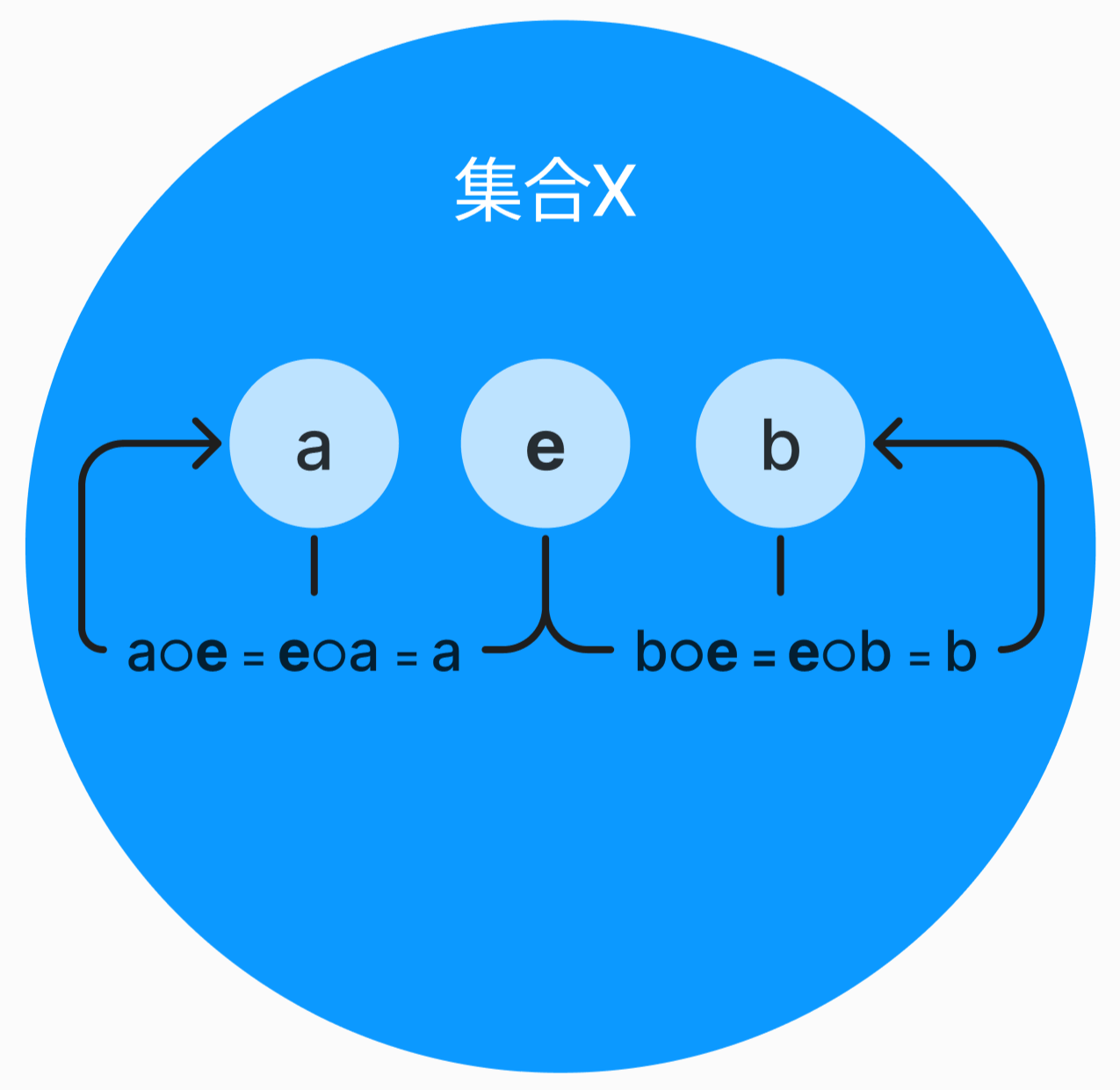
単位元のイメージ
このような単位元が存在することという条件を、「単位元」「単位元の存在」「単位元が存在する」「単位律」などといいます。

きました！単位律！

先ほどの自然数全体の集合${\footnotesize \mathbb{N}}$と足し算の例では、単位元は${\footnotesize 0}$になります。
何故なら

$${\footnotesize 0 + a = a + 0 = a \mid a\in \mathbb{N}}$$

ということで、どの自然数に0を足しても値は変わらないからです。
二項演算として掛け算を考えるなら${\footnotesize 1}$が単位元になります。
何故なら

$${\footnotesize 1 \times a = a \times 1 = a \mid a\in \mathbb{N}}$$

だからです。

また、単位元を定義したとき、左にも右にも単位元が出てきましたが、${\footnotesize e\circ a = a}$を成り立たせるのが、左単位元 ${\footnotesize e}$で、${\footnotesize a \circ e = a}$を成り立たせるのが右単位元 ${\footnotesize e}$です。
左単位律は左単位元が存在すること、右単位律は右単位元が存在すること、という条件になります。

任意の元の左右が入れ替わっても二項演算${\circ}$の結果が変わらないとき、二項演算${\footnotesize \circ}$は可換と言います。
可換であるならば、単位元に左右の区別をつける必要はなく、律もシンプルに単位律になります。

ここまでが単位律の説明です。
長かった。

予備知識 - 結合律

結合律の説明でも集合${\footnotesize X}$とその任意の元${\footnotesize a,b}$に対して定められた二項演算${\footnotesize \circ}$を用います。

結合律とは${\footnotesize a,b,c\in X}$に対して

$${\footnotesize (a\circ b)\circ c = a\circ(b\circ c)}$$

が成り立つということを表します。
これは二項演算を行う順序によって結果が変わらないということです。

例えば具体的な集合${\footnotesize X}$として整数全体からなる集合${\footnotesize \mathbb{Z}}$を考えてみましょう。
二項演算として足し算を考えるなら結合律を満たすことがわかるかと思います。
では引き算ならどうでしょう？
${\footnotesize 1 - (2 - 3) \neq (1 - 2) - 3}$
という例を挙げることができるので、必ずしも結合律を満たすとは限りませんね。

これが結合律です。

---

では準備が整ったので、モナド則の意味を説明していきます。

代数的構造の律とモナド則の律を比較する

ここまで見てきた代数的構造における各律と、モナド則における各律を比較してみましょう。
ここから何が読み取れるでしょうか。

律	代数的構造	モナド則
左単位律	${\footnotesize e\circ a=a}$	pure a >>= f == f a
右単位律	${\footnotesize a\circ e=a}$	m >>= pure == m
結合律	${\footnotesize (a\circ b)\circ c = a\circ(b\circ c)}$	(m >>= g) >>= h == m >>= (\x -> g x >>= h)

こう見比べてみるとモナド則では>>=が二項演算にあたるということがわかると思います。
集合は『型すべてからなる集合』と考えられます。
>>=は左辺と右辺で型が異なりますが、二つの型(二つ目は関数だけどこれは関数型という型)をとり別の型に写すという意味でちゃんと二項演算になっています。

では続いて具体的にモナド則の『左単位律』『右単位律』『結合律』がどのような意味合いなのかを説明します。

左単位律: pure a >>= f == f a

代数的構造における左単位律とは「左単位元 ${\footnotesize e}$が存在する」という条件でした。
そして左単位元 ${\footnotesize e}$とは、次のように二項演算において結果に影響しない元なのでした。

$${\footnotesize e\circ a=a}$$

ここから、モナド則の左単位律も同じように二項演算において結果に影響しない左単位元が存在するという条件だと考えることができます。

その左単位元は>>=を二項演算とするとpure aになります。
つまり「pure aは>>=の結果に影響を与えてはならぬ」ということをいっていそうです。

コードを見ながら確認してみましょう。

コードでは左単位律はpure a >>= f == f aとなっています。
これはa型の値を関数pureと>>=を経由して関数fに適用したものと、直接関数fに適用させた結果は同じであるということです。

各関数の型まで描くとこうなります。

pureとはa -> m aという定義で、a型の値をm a型の値に持ち上げる関数でした。
そして>>=(bind)の定義はm a -> (a -> m b) -> m bで、計算を行う際m aからaを取り出して、関数fに適用させ、その結果を返す関数です。
右辺と異なり左辺はこれだけのことが行われた結果なので、処理のどこかでaやf aの結果に変更が加えられた場合、等式が成り立たなくなることが考えられます。

実現可能性を度外視して変更を加えるパターンを挙げるならば次のようなものが考えられるでしょう。

• pureの処理の中でaに手を加える
• >>=の処理でm aからaを取り出して手を加えたものをfに適用させる
• >>=の処理でaをfに適用させた結果に手を加える
  

つまりpureだけでなく、>>=も左単位律を満たさなくなることをしてはいけないのです。
これは代数的構造の左単位律とは異なる点です。

しかし「二項演算に影響を与えない」という意味は代数的構造の左単位律と共通していますね。

右単位律: m >>= pure == m

代数的構造における右単位律とは「右単位元 ${\footnotesize e}$が存在する」という条件でした。
そして右単位元 ${\footnotesize e}$とは、次のように二項演算において結果に影響しない元なのでした。

$${\footnotesize a\circ e=a}$$

ここから、左単位律と同様に右単位律でも二項演算において結果に影響しない右単位元が存在するという条件だと考えることができます。

右単位律の場合の右単位元は>>=を二項演算としてpureになります。
右単位律は「pureは>>=の結果に影響を与えてはならぬ」ということをいっていそうです。

コードを見て確認してみましょう。

右単位律を表すコードはm >>= pure == mです。
左単位律ではpure aだったところがmになっていますが、このmはpure aの結果と同じです。
つまりモナドの型の値です。この値がどのように作られたかは言及されていません。
また、pure: a -> m aは左単位律のf: a -> m bと「aがbに写すかaのままか」という違いはあれ同じ構造(同じ関数型)をしています。

冗長に書きましたが、このコードは「mとpureを>>=に適用させたときは、元のmと等しくなければならない」という意味になります。
pureを関数として右辺で使った場合も>>=の結果に影響を与えてはいけないということです。
なんか左単位律よりシンプルですね。

左単位律のときと同様に各関数の型まで描くとこうなります。

これも左単位元律と同じく、pureや>>=が余計なことをすると条件を満たさなくなります。

こちらも「二項演算に影響を与えない」という意味で代数的構造の右単位律と共通しています。

結合律: (m >>= g) >>= h == m >>= (\x -> g x >>= h)

代数的構造では結合律は${(a\circ b)\circ c = a\circ(b\circ c)}$でした。
モナド則の方では、二項演算を>>=とすると左辺はまったく同じ形をしています。
右辺の方はちょっと違う形をしていますね。
あらためて書くまでもないことですが代数的構造において右辺では${b\circ c}$が先に計算されます。
ではモナド則の右辺はどうなのか、というと(\x -> g x >>= h)は関数型なので先に計算が行われるわけではありません。

意味としては、g: a -> m b, h: b -> m cという関数があったとき、どういう順序で結合したとしても結果は等しくなるという意味です。
この条件にはpureは登場せず、>>=にのみ着目した条件になります。

こちらは代数的構造の結合律に非常に近しい形をしているし、意味もわかりやすいので、これ以上の説明はいらないでしょう。
左辺と右辺の動作の違いがよくわからないかもしれませんが、その場合は後続の結合律を満たさない例の節の図解を見ていただくとイメージがつくかと思います。

モナド則 - おわりに -

長々と説明してきましたが、モナド則の各条件の名称の意味を知った上で、あらためてコードを見てみると、ちゃんと名称通りになっていることや、条件が何をいっているのかが理解しやすかったのではないでしょうか。

モナド則の説明は一旦ここまでさせていただき、ここからはモナド則を満たさない場合の話をしていきます。

モナド則を満たさないとどうなるか

モナド則を満たしていないとどうなるでしょうか。
なぜモナド則を満たさないといけないのでしょうか。

この疑問に答えるため、モナド則を満たさないモナドを作ってみようと思います。
「それはモナドじゃないんじゃないか？」
と思われるでしょうが

その通りだけど、そうじゃない

です。

「その通り」というのは、「モナド則を満たしていないので、モナドとはいえない」というそのまんまの意味です。
「そうじゃない」というのは、最初の方で書いた通り、「一部の特性を持ったプログラミング言語以外はモナド則を満たさなくてもプログラム上コンパイルエラーになったりせず、モナドを作ることができてしまう」という意味です。

ということで、あえてモナド則を満たさない壊れたモナドを作ってみます。

単位律を満たさない例

まず単位律を満たさないことを表すためのデータ型を作ってみます。

newtype Broken a = Broken a

単位律のところでpure関数や>>=関数はa型に余計な加工をしてはいけないと書きましたが、余計なことをしてやろうじゃないですか。
といったものの上記定義のa型は、任意の型です。
そして何の制約も持たない型です。
aに具体的な型を与えるまではaはどのような関数に適用することができないということです。

例えば、pureでaをa + aみたいにしてやろうと考えて、次のように足し算できる制約をつけてやろうとしてもコンパイルエラーになります。

newtype Broken a = Ring a => Broken a

ではnewtypeの定義でやるのは諦めて、pureにシグニチャを書いてやって制約を与えて、値を改変したらどうか、と思っても駄目です。

instance Applicative Broken where
  pure :: forall a. Ring a => a -> Broken a
  pure a = Broken (a + a)
--  No type class instance was found for
--
--    Data.Ring.Ring a0

ということで用意したのがこういう型です。

newtype UnitLawBroken a = UnitLawBroken (Maybe a)

a型を直接使うのではなく、Maybe型でラップしています。
そしてpureはこのようにして、何が適用されようとNothingにしてしまいます。めちゃくちゃです。

instance Applicative UnitLawBroken where
  pure _ = UnitLawBroken Nothing

bindは素直に実装して、期待通り動くようにします。

instance Bind UnitLawBroken where
    bind (UnitLawBroken a) f = case a of
      Just a' -> f a'
      Nothing -> UnitLawBroken Nothing

instance Monad UnitLawBroken

省略していますが、Functor,Apply,Show,Eqなどのインスタンスにもしています。

コード全体

UnitLawBroken.purs

module Study.Control.Monad.LawBroken.UnitLawBroken where

import Prelude

import Data.Maybe (Maybe(..))

newtype UnitLawBroken a = UnitLawBroken (Maybe a)

instance Show a => Show (UnitLawBroken a) where
  show (UnitLawBroken a) = show a

instance Eq a => Eq (UnitLawBroken a) where
  eq (UnitLawBroken a) (UnitLawBroken b) = a == b

instance Functor UnitLawBroken where
  map f (UnitLawBroken a) = UnitLawBroken (f <$> a)

instance Apply UnitLawBroken where
  apply (UnitLawBroken f) (UnitLawBroken a) = UnitLawBroken (f <*> a)

instance Applicative UnitLawBroken where
  pure _ = UnitLawBroken Nothing

instance Bind UnitLawBroken where
  bind (UnitLawBroken a) f = case a of
    Just a' -> f a'
    Nothing -> UnitLawBroken Nothing

instance Monad UnitLawBroken

pureでaの値を捨ててしまっているので、単位律は満たせなくなっているはずです。

ではテストしてみましょう。

shouldNotEqualで「等しくないこと」を検証しています。

spec :: Spec Unit
spec = do
  describe "単位元律を満たさない" do
    it "左単位元律を満たさない: pure a >>= f ≠ f a" do
      let
        a = "a"
        f = \x -> UnitLawBroken (Just x)
      (pure a >>= f) `shouldNotEqual` (f a)
    
    it "右単位元律を満たさない: m >>= pure ≠ m" do
      let m = UnitLawBroken (Just "a")
      (m >>= pure) `shouldNotEqual` m

  describe "結合律を満たす" do
    it "(m >>= f) >>= g == m >>= (\x -> f x >>= g)" do
      let
        m = UnitLawBroken (Just "a")
        f = \x -> UnitLawBroken (Just $ x <> "b")
        g = \x -> UnitLawBroken (Just $ x <> "c")
      ((m >>= f) >>= g) `shouldEqual` (m >>= (\x -> f x >>= g))

このテストは全部パスします。

単位元律を満たさない
  ✓︎ 左単位元律を満たさない: pure a >>= f ≠ f a
  ✓︎ 右単位元律を満たさない: m >>= pure ≠ m
結合律を満たす
  ✓︎ (m >>= f) >>= g == m >>= ( -> f x >>= g)

ではshouldNotEqualをshouldEqualに変えるとどうなるかというと、このようなテスト結果になります。

単位元律を満たさない
  ✗ 左単位元律を満たさない: pure a >>= f ≠ f a:

  Nothing ≠ (Just "x")
  ✗ 右単位元律を満たさない: m >>= pure ≠ m:

  Nothing ≠ (Just "x")
結合律を満たす
  ✓︎ (m >>= f) >>= g == m >>= ( -> f x >>= g)

a型をそのまま使わずMaybe型でラップしたのは、反則気味に感じられたかもしれませんが、こういうラッパー型はよく作ると思うので気をつけないといけませんね。

単位律を満たさないとどうなるか

モナドを使う側になって考えてみましょう。

pure関数を使うユースケースとしては、モナドを用いた計算における起点や、計算の戻り値を返すときなどが考えられると思いますが、それらすべてが期待通り動かなくなるでしょう。

期待通り動かしたいのならば、pure aではなくUnitLawBroken (Just a)のように直接書くことになるでしょう。
その場合、文脈に持ち上げたいという意図を示すことはできなくなります。
直接書くにしてもデータコンストラクタがexportされていなければできません。

結合律を満たさない例

単位律の話では、a型をラップしましたが、結合律ではa型と別の型も持つようにして、そちらを変更するというアプローチをとろうと思います。

まず型を定義するのですが、単位律のところで書いたように、今度はa型と別の型を持たせることにします。

newtype AssociativeLawBroken v a = AssociativeLawBroken { value :: v, a :: a }

型構築子のaの前にvがおり、レコード型のフィールドvalueの型とします。
このvに制約をつけてやるわけです。

やってみましょう。
まずはpureです。

instance Ring r => Applicative (AssociativeLawBroken r) where
  pure a = AssociativeLawBroken {value: zero, a: a}

vの箇所に入るrはRingという型クラスの制約がついています。
Ringとは代数的構造の「環」を表す型クラスです。
雑に説明すると足し算・掛け算・引き算ができるというインタフェースみたいなやつです。

定義

Ringとその親クラスのSemiringのコードの一部です。
addは足し算、zeroは足し算に関する単位元、mulは掛け算、oneは掛け算に関する単位元です。
subは引き算です。

class Semiring a where
  add :: a -> a -> a
  zero :: a
  mul :: a -> a -> a
  one :: a

infixl 6 add as +
infixl 7 mul as *

class Semiring a <= Ring a where
  sub :: a -> a -> a

infixl 6 sub as -

IntはRingとSemiringのインスタンスになっています。

instance semiringInt :: Semiring Int where
  add = intAdd
  zero = 0
  mul = intMul
  one = 1

instance ringInt :: Ring Int where
  sub = intSub

続いて今回肝心のbindです。
rにRingの制約がついていることで引き算ができるようになっており、戻り値を返す前にvalueの値を引いています。

instance Ring r => Bind (AssociativeLawBroken r) where
  bind (AssociativeLawBroken {value: v, a}) f = do
    let AssociativeLawBroken {value: v', a: a'} = f a
    AssociativeLawBroken {value: v - v', a: a'}

なんでこんなことをしているかというと、引き算は結合律を満たさないからですね。

コード全体

AssociativeLawBroken.purs

import Prelude

newtype AssociativeLawBroken v a = AssociativeLawBroken { value :: v, a :: a }

instance Ring r => Functor (AssociativeLawBroken r) where
  map f (AssociativeLawBroken {value, a}) = AssociativeLawBroken {value, a: (f a)}

instance Ring r => Apply (AssociativeLawBroken r) where
  apply (AssociativeLawBroken {value: v1, a: f}) (AssociativeLawBroken {value: v2, a: a})
    = AssociativeLawBroken {value: v1 - v2, a: f a}

instance Ring r => Bind (AssociativeLawBroken r) where
  bind (AssociativeLawBroken {value: v, a}) f = do
    let AssociativeLawBroken {value: v', a: a'} = f a
    AssociativeLawBroken {value: v - v', a: a'}

instance Ring r => Applicative (AssociativeLawBroken r) where
  pure a = AssociativeLawBroken {value: zero, a: a}

instance Ring r => Monad (AssociativeLawBroken r)

instance (Show r, Show a) => Show (AssociativeLawBroken r a) where
  show (AssociativeLawBroken {value, a}) = "{value: " <> show value <> ", a: " <> show a <> "}"

instance (Eq r, Eq a) => Eq (AssociativeLawBroken r a) where
  eq (AssociativeLawBroken {value: v1, a: a1}) (AssociativeLawBroken {value: v2, a: a2}) = v1 == v2 && a1 == a2

これで結合律が破れるかテストしてみましょう。

spec :: Spec Unit
spec = do
  describe "Monad則" do
    describe "結合律を満たさない" do
      it "(m >>= f) >>= g ≠ m >>= (\x -> f x >>= g)" do
        let
          m = AssociativeLawBroken {value: 1, a: unit}
          f = \a -> AssociativeLawBroken {value: 2, a}
          g = \a -> AssociativeLawBroken {value: 3, a}
        ((m >>= f) >>= g) `shouldNotEqual` (m >>= (\x -> f x >>= g))

結果はテストをパスします。

Monad則 » 結合律を満たさない
  ✓︎ (m >>= f) >>= g ≠ m >>= ( -> f x >>= g)

shouldEqualに変えるとテストは落ちます。

Monad則 » 結合律を満たさない
  ✗ (m >>= f) >>= g ≠ m >>= ( -> f x >>= g):

  {value: -4, a: unit} ≠ {value: 2, a: unit}

念の為テストコードの説明をしておきましょう。
まず、これは引き算が結合律を満たさないことを確認する
$\footnotesize {(1 - 2) - 3 \neq 1 - (2 - 3)}$
という等式をモナドで再現しようとしたものになります。
だからvalue: 1とかvalue: 2とかが出てきます。

次にaが軒並みunitになっているのは今回のテストとしては「どうでもいいから」です。
このaは前述したように手を加えられず、代わりにvalueの方を加工しているわけなので今回見たいのはvalueの方なのです。だからaは別に空文字でも何でもいいです。

最後に再度テストコードの等式と>>=の実装を見て、具体的に左辺と右辺がどのような動作をした結果が異なるようになったか見ていきましょう。
まずコードの抜粋です。

-- テストコード部分
let
  m = AssociativeLawBroken {value: 1, a: unit}
  f = \a -> AssociativeLawBroken {value: 2, a}
  g = \a -> AssociativeLawBroken {value: 3, a}
((m >>= f) >>= g) `shouldNotEqual` (m >>= (\x -> f x >>= g))

-- >>=の実装部分
bind (AssociativeLawBroken {value: v, a}) f = do
  let AssociativeLawBroken {value: v', a: a'} = f a
  AssociativeLawBroken {value: v - v', a: a'}

単位律と比べてこちらの動作の違いはわかりづらいかと思いましたので図解したものを用意しました。

(m >>= f) >>= g == m >>= (\x -> f x >>= g)の左辺と右辺の動作の図

do記法で書いたときの影響

結合律が満たされていない場合のdo記法への影響も見ておきましょう。

まずMaybeモナドを使ってコードを書いてみます。

let
  m = Just 1
  f = \a -> Just (a - 2)
  g = \a -> Just (a - 3)

  result = do
    a <- m
    b <- f a
    g b
  
Just (-4) `shouldEqual` result

このdo記法の部分は次のように書くこともできます。

result = do
  x <- do
    a <- m
    f a
  g x

更に別の書き方もできます。

result = do
  a <- m
  do
    x <- f a
    g x

これらは同じ結果を返します。

let
  result1 = do
    x <- do
      a <- m
      f a
    g x
  result2 = do
    a <- m
    do
      x <- f a
      g x
result1 `shouldEqual` result2 

さて、結合律を満たさないモナドで上記と同じコードを書いたらどうなるか。
テストしてみましょう。

it "(m >>= f) >>= g ≠ m >>= (\x -> f x >>= g) (do記法)" do
  let
    m = AssociativeLawBroken {value: 1, a: unit}
    f = \a -> AssociativeLawBroken {value: 2, a}
    g = \a -> AssociativeLawBroken {value: 3, a}

    result1 = do
      x <- do
        a <- m
        f a
      g x
    result2 = do
      a <- m
      do
        x <- f a
        g x
  result1 `shouldEqual` result2

これはテストをパスしません。

✗ (m >>= f) >>= g ≠ m >>= ( -> f x >>= g) (do記法):

{value: -4, a: unit} ≠ {value: 2, a: unit}

do記法は>>=のsyntax sugarなのだから当然っちゃあ当然なのですが、このように書き方によって結果が変わるんじゃ使いづらいですよね。

やはり結合律は満たさないと困りますし、結合律が満たされていることはありがたいのです。

おわりに

最初はちょっとモナド則のコードを解説する程度の記事を書くつもりだったのですが、「これじゃ説明が飛躍してないか？」とか「これで伝わるのか？」という疑問が湧いてきて、あれこれ書き加えていたらとても長い記事になってしまいました。
前置きも長いし。

最後まで読んでくれた奇特な方に感謝を述べつつ、記事を終えたいと思います。

このようなトピックの記事でしかも長いけど読んでくださりありがとうございます。