圏論のモナドとPureScriptのモナドの関係性を知ろう

この記事が目指すところ

この記事は圏論のアレやコレが具体的なプログラミング言語ではどうなっているのかを解説することで、圏論のような数学的概念とプログラミング言語にどういう繋がりがあるのかを知っていただくことを目的としています。

特にみんなが大好きな「モナド」にフォーカスします。
したがってモナドの定義にあらわれる「関手」「自然変換」などにも言及します。

具体的なプログラミング言語としてはPureScriptを用います。

前置き

この記事の基本構成

この記事は圏論の「圏」「関手」「自然変換」「モナド」について以下を繰り返しながら進んでいくという構成になっています。

1. 圏論側の定義や概念を示す
2. 1とPureScript側がどう対応しているのかを説明する

前提となる知識

圏論、PureScriptともに基礎的な知識を前提としています。
具体的にいうと、圏論においては圏・関手・自然変換あたりの知識で、PureScriptにおいてはFunctor・Monadあたりの知識です。
とはいえ必要な定義は書いていますし、解説・補足などを適宜行っていくので、ざっくり知っているくらいでも大丈夫かと思います。

圏論の諸概念の定義について

圏論の諸概念の定義は可能な限り何らかの圏論のテキストを元にしました。
（記号などは記事内での一貫性を担保するため変えたりしていますが）
こういった定義に関わるような文章に関しては、「～である」「～だ」のような常体で書き、解説・補足に該当するような文章に関しては「です」「ます」のような敬体で書くことで区別できるようにしています。定義と解説・補足の文章を水平線で分割したりもしています。

書いていないこと

記事の目的のみにフォーカスするため次のようなことは書いておりません。

• いわゆる証明
• この記事のモナドの説明に出てこない圏論の概念の説明（例えば双対圏とか、反変関手とか、随伴とか）
• PureScriptのFunctorやMonadなどの使い方自体（使い方は圏論の学習ではなく、実際モナドを使ったコードを書く、自分でモナドを作るなどして覚えることをおすすめします）

他にもあるかもしれませんが、ただでさえ絞っても分量が多くなる内容なので、基本的に必要最低限のものを書くスタンスです。

---

さあ前置きはこのへんにして、はじめましょう！

ざっくりとした関係性

このあと一つずつ見ていきますが、まずざっくりと関係性を示した図を示します。
これは圏論のモナドに関わる概念からPureScript側の概念への関連の図です。
圏論側にあって、PureScript側にないものがあるかと思いますが、これは圏論のモナドを定義する上で登場しない概念です。
つまりPureScriptのApplyは圏論におけるモナドの定義には登場しないことを意味します。

一つずつ見ていきましょう。

圏

まず圏論における圏の定義を示します。

【定義】圏

圏${\footnotesize \mathcal{A}}$とは

• 対象${\footnotesize (\mathrm{object})}$の集合${\footnotesize \mathrm{ob}(\mathcal{A}) }$
• 各${\footnotesize A,B\in \mathrm{ob}(\mathcal{A})}$について、${\footnotesize A}$から${\footnotesize B}$への射(${\footnotesize \mathrm{map}}$)の集合${\footnotesize \mathcal{A}(A,B) }$
• 各${\footnotesize A,B,C\in \mathrm{ob}(\mathcal{A})}$について、合成と呼ばれる関数

$${\footnotesize \begin{darray}{cc} \mathcal{A}(B,C) \times \mathcal{A}(A,B) & \rightarrow & \mathcal{A}(A,C)\\ (g,f) & \mapsto & g\circ f \end{darray}}$$

• 各${\footnotesize A\in \mathrm{ob}(\mathcal{A})}$について、${\footnotesize A}$上の恒等射と呼ばれる${\footnotesize \mathcal{A}( A,A)}$の元 ${\footnotesize 1_{A}}$

からなり、以下の公理を満たすもののことである。

• 結合律：任意の${\footnotesize f\in \mathcal{A}( A,B), g\in \mathcal{A}( B,C) , h\in \mathcal{A}( C,D)}$について
  ${\footnotesize (h\circ g) \circ f=h\circ ( g\circ f)}$ が成り立つ。
• 単位律：任意の${\footnotesize f\in \mathcal{A}(A,B)}$について
  ${\footnotesize 1_{A} \circ f=f=f\circ 1_{B}}$ が成り立つ。
  
  図:圏の例

可換

一般的に図式が可換であるとは、対象${\footnotesize X}$から${\footnotesize Y}$への経路が二つ以上あるならいつでも、片方の経路に沿った合成で得られる${\footnotesize X}$から${\footnotesize Z}$への射が、他に沿った合成で得られる射と等しいことをいう。
例えば次のように与えられた圏の対象と射について${\footnotesize g\circ f=i\circ h}$のとき図式は可換であるという。

恒等射と対象の同一視

対象と恒等射は一対一の対応があるため、対象を恒等射と同一視することができる。

例えば上記の対象${\footnotesize Y}$に対して対応する恒等射${\footnotesize 1_Y}$は一意に定まるため、${\footnotesize Y:Y\rightarrow Y}$のように恒等射${\footnotesize 1_Y}$を対象${\footnotesize Y}$そのものと同一視し、${\footnotesize 1_Y=Y}$とする。
このように同一視するモチベーションは、こうした方が便利な場合があるからである。

PureScriptの圏

次にPureScript側のコードを示します。
PureScriptにはまんま圏を表すCategoryという型クラスがあります。
そしてCategoryはSemigroupoidという型クラスを継承したものになっています。

Control.Category

class Category :: forall k. (k -> k -> Type) -> Constraint
class Semigroupoid a <= Category a where
  identity :: forall t. a t t

instance categoryFn :: Category (->) where
  identity x = x

Control.Semigroupoid

class Semigroupoid :: forall k. (k -> k -> Type) -> Constraint
class Semigroupoid a where
  compose :: forall b c d. a c d -> a b c -> a b d

instance semigroupoidFn :: Semigroupoid (->) where
  compose f g x = f (g x)

infixr 9 compose as <<<

Semigroupoidは数学的には代数的構造の一種で、圏から恒等射および単位法則を除いた構造になっています（参考）。

まずSemigroupoidの方を見てみると、Semigroupoidにはcomposeという関数が定義されており、Semigroupoidのインスタンスとして->のインスタンスが定義されています。
->は関数なので、ここにはPureScriptの関数の合成が定義されているということになります。

またcomposeのエイリアスとして<<<が定義されていますね。関数合成としてはこちらを使うことがほとんどだと思いますが実はcomposeという関数だったのですね。

一方、Categoryの方を見てみると、こちらにはidentityという関数が定義されています。

圏論においての圏とPureScriptのCategoryの関係性

まず圏論の圏はかなり抽象的な定義となっており、条件さえ満たせば対象と射はどのようなものでも圏を構成することができます。

ではPureScriptのCategoryはどのような圏になるでしょうか？

まずPureScriptにおいての対象はPureScriptの型となります。
そしてそれらの間の関数が射となります。
（このような圏をHaskell界隈ではHaskellの型の圏Haskというようです）

圏における射の合成は、PureScriptでいうとSemigroupoidのcomposeにあたります。
恒等射は、PureScriptでいうとCategoryのidentityになります。

結合律・単位律

PureScriptは関数自体の比較が行えないため、関数自体を用いて結合律や単位律を満たすかどうかを検証することはできません。

しかし具体的な値と関数を用いれば（あくまでその具体化されたものに対しては）検証することができるのでテストコードを書いてみます。

Test.Main

module Test.Main where

import Prelude

import Data.Number (isNaN)
import Data.String (length)
import Effect (Effect)
import Effect.Aff (launchAff_)
import Test.Spec (describe, it)
import Test.Spec.Assertions (shouldEqual)
import Test.Spec.Reporter (consoleReporter)
import Test.Spec.Runner (runSpec)

main :: Effect Unit
main = launchAff_ $ runSpec [consoleReporter] do
  describe "Categoryは以下の条件を満たす" do
    let 
      f = isNaN
      g = show
      h = length
      a = 100.0
    it "結合律を満たす" do
      ((h <<< g) <<< f) a `shouldEqual` (h <<< (g <<< f)) a

    it "左単位律を満たす" do
      (identity <<< f) a `shouldEqual` f a

    it "右単位律を満たす" do
      f a `shouldEqual` (f <<< identity) a

実行結果

Categoryは以下の条件を満たす
  ✓︎ 結合律を満たす
  ✓︎ 左単位律を満たす
  ✓︎ 右単位律を満たす

まとめ

圏論の圏と、PureScriptのCategoryの対応をまとめてみます。

圏の定義で使った圏の例とともに、PureScriptの圏の例を示します。

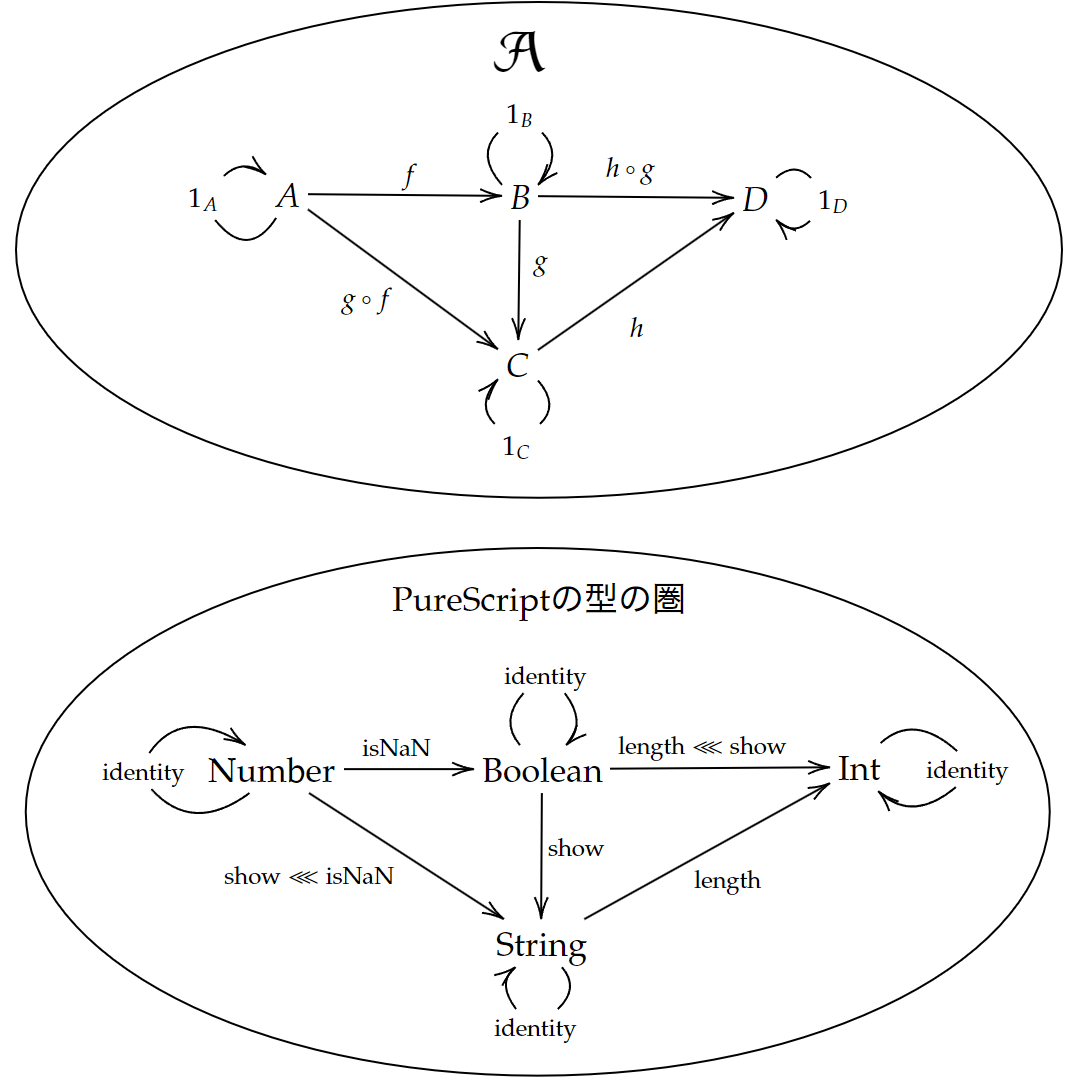
関手

圏と同様にまず圏論における関手の定義を示します。

【定義】関手

${\footnotesize \mathcal{A}, \mathcal{B}}$を圏とする。
関手${\footnotesize F:\mathcal{A}\rightarrow \mathcal{B}}$ とは

• ${\footnotesize X\mapsto F(X)}$と書かれる関数
  
  $${\footnotesize \ \mathrm{ob}(\mathcal{A})\rightarrow \mathrm{ob}(\mathcal{B})}$$
• ${\footnotesize X,Y\in \mathcal{A} }$ について ${\footnotesize f\mapsto F(f)}$ と書かれる関数
  
  $${\footnotesize \mathcal{A}( X,Y)\rightarrow \mathcal{B}( F(X) ,F(Y))}$$

からなり、以下を満たすものである。

• ${\footnotesize \mathcal{A}}$ で ${\footnotesize X\xrightarrow{f} Y\xrightarrow{g} Z}$ となるものについて
  
  $${\footnotesize F(g\circ f) = F(g) \circ F(f)}$$
• ${\footnotesize X\in \mathcal{A}}$ について
  
  $${\footnotesize F(\mathrm{1}_{X}) = \mathrm{1}_{F(X)}}$$
  
  
  図:関手の例

---

関手の条件における ${\footnotesize F(g\circ f) =F(g) \circ F(f)}$は 射の合成を保つことを表し、${\footnotesize F(1_{X}) =\mathrm{1}_{F(X)}}$は 恒等射を保つということを表しています。

「保つ」というのは「構造を保つ」ということを意味しています。この表現は集合論や代数学では本当によく目にする表現ですが、この記事においては、条件の呼び方として使いたいだけなので、よくわからなくても大丈夫です。

また関手において、対象についての関数${\footnotesize X\mapsto F(X)}$を対象関数、
射についての関数 ${\footnotesize f\mapsto F(f)}$ を射関数と呼ぶことがあるようです。
私が読んだ書籍『ベーシック圏論』ではこの言葉は使われていませんでしたが、Web上では使われている例をしばしば見かけました。
便利なので本記事では以後この言葉を使っていきます。

【定義】関手の合成

${\footnotesize \mathcal{A} ,\ \mathcal{B,\ C}}$を圏としたとき
関手

$${\footnotesize F:\mathcal{A}\rightarrow \mathcal{B}, G:\mathcal{B}\rightarrow \mathcal{C}}$$

に対して、関手の合成

$${\footnotesize G\circ F:\ \mathcal{A}\rightarrow \mathcal{C}}$$

を以下で定める。

1. ${\footnotesize G\circ F:\ X\rightarrow G( F( X)) ( \ X\in \mathrm{ob}(\mathcal{A}) ,\ G( F( X)) \in \mathrm{ob}(\mathcal{C}) \ )}$
2. ${\footnotesize G\circ F:\ f\rightarrow G( F( f)) ( f\in \mathcal{A}( X,\ Y) ,\ G( F( f)) \in \mathcal{C}( \ G( F( X)) ,\ G( F( Y)) \ )}$

1は対象関数の合成で、2は射関数の合成です。

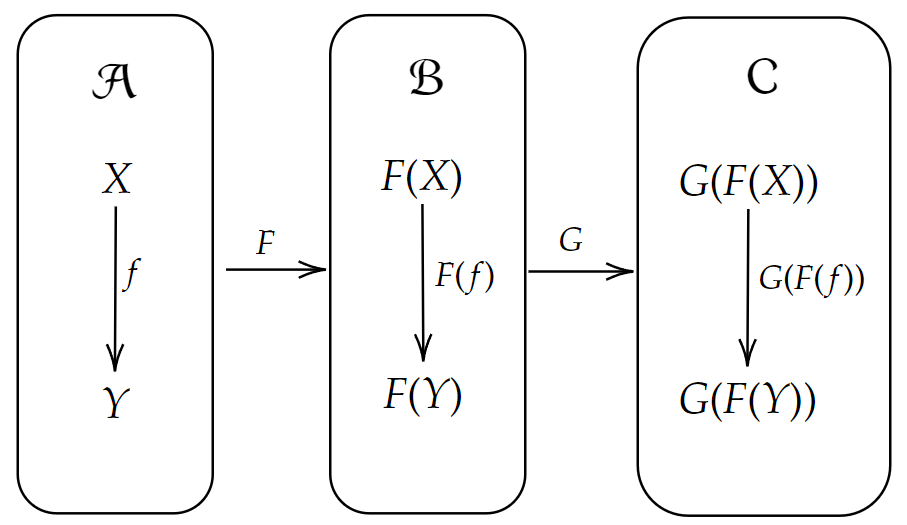
図:関手の合成

【定義】恒等関手

${\footnotesize \mathcal{A}}$を圏としたとき

恒等関手 ${\footnotesize 1_{\mathcal{A}} :\mathcal{A}\rightarrow \mathcal{A}}$ を以下で定める

1. ${\footnotesize 1_{\mathcal{A}} :X\rightarrow X ( X\in \mathrm{ob}(\mathcal{A}))}$
2. ${\footnotesize 1_{\mathcal{A}} :\ f\rightarrow f ( f\in \mathcal{A}( X,\ Y) \ )}$

図:恒等関手はすべての対象と射をそれ自身へと写す

【定義】自己関手

圏${\footnotesize \mathcal{A}}$から同じ圏${\footnotesize \mathcal{A}}$への関手は自己関手と呼ばれる。
すなわち恒等関手は、自己関手である。

PureScriptの関手

PureScriptの関手は射関数と対象関数に分けて見ていきます。

射関数

PureScriptにはFunctorという型クラスが存在します。

Data.Functor

class Functor f where
  map :: forall a b. (a -> b) -> f a -> f b

このFunctorにはmapという関数が定義されていますが、これは圏論の関手でいうと射関数にあたるものです。
次の図は、対象や関手の名前を上記のmapの定義に合わせた形で描いたものです。

赤字のところに着目してください。
map関数の定義forall a b. (a -> b) -> f a -> f bと一致していますね。
括弧をつけてやり(a -> b) -> (f a -> f b)、つまりmap関数を、関数(a -> b)を関数(f a -> f b)に写すものと考えるとより圏論の定義に近い形に見えるでしょう。

対象関数

PureScriptでは型構築子が関手の対象関数と考えられます。
例えばMaybeの型構築子は、型aを型Maybe aに写します。
MaybeはFunctorのインスタンスになっているので射関数も備えています。
Maybeを例に対象関数と射関数を図にしてみます。

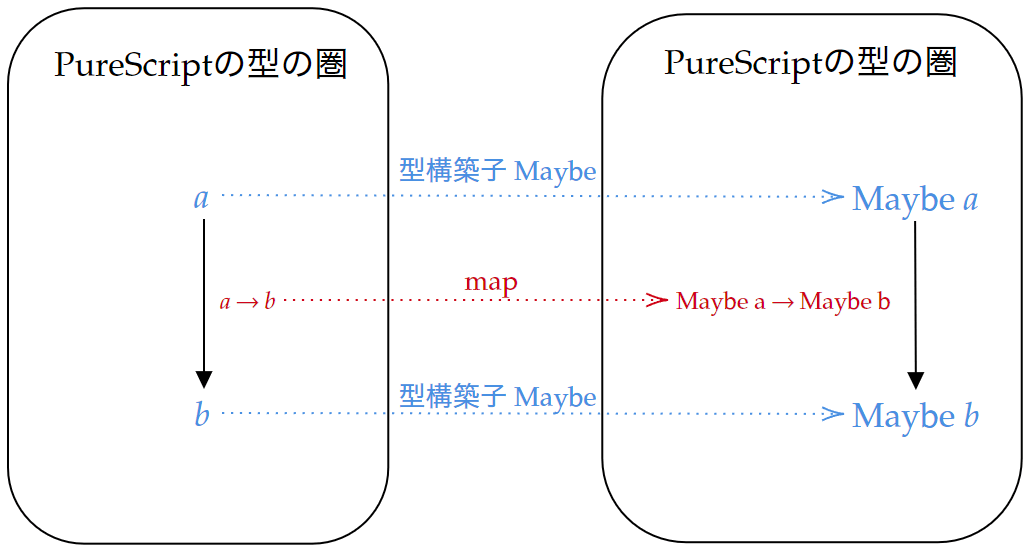
Functor則

圏論の関手には、射の合成を保つこと、恒等射を保つことという条件がありました。
PureScriptのFunctorにおいてはこの条件をFunctor則と呼びます。
Categoryのときと同様に、具体的な型Maybe Numberを使ってFunctor則を満たすか検証するコードを書いてみます。

Test.Main

module Test.Main where

import Prelude

import Data.Maybe (Maybe(..))
import Data.Number (isNaN)
import Effect (Effect)
import Effect.Aff (launchAff_)
import Test.Spec (describe, it)
import Test.Spec.Assertions (shouldEqual)
import Test.Spec.Reporter (consoleReporter)
import Test.Spec.Runner (runSpec)

main :: Effect Unit
main = launchAff_ $ runSpec [consoleReporter] do
  describe "Maybe NumberはFunctor則を満たす" do
    it "射の合成を保つ" do
      let 
        a = Just 1.0
        f = isNaN
        g = show
      (map (g <<< f) a) `shouldEqual` ((map g <<< map f) a)
    
    it "恒等射を保つ" do
      let a = Just 1.0
      map identity a `shouldEqual` identity a

実行結果

Maybe NumberはFunctor則を満たす
  ✓︎ 射の合成を保つ
  ✓︎ 恒等射を保つ

自己関手

自己関手とは、圏${\footnotesize \mathcal{A}}$から同じ圏${\footnotesize \mathcal{A}}$への関手でした。
そしてPureScriptの関手は、PureScriptの型の圏からPureScriptの型の圏への関手なので、自己関手ということになります。

まとめ

あらためて圏論の関手とPureScriptのFunctorを比べてみます。

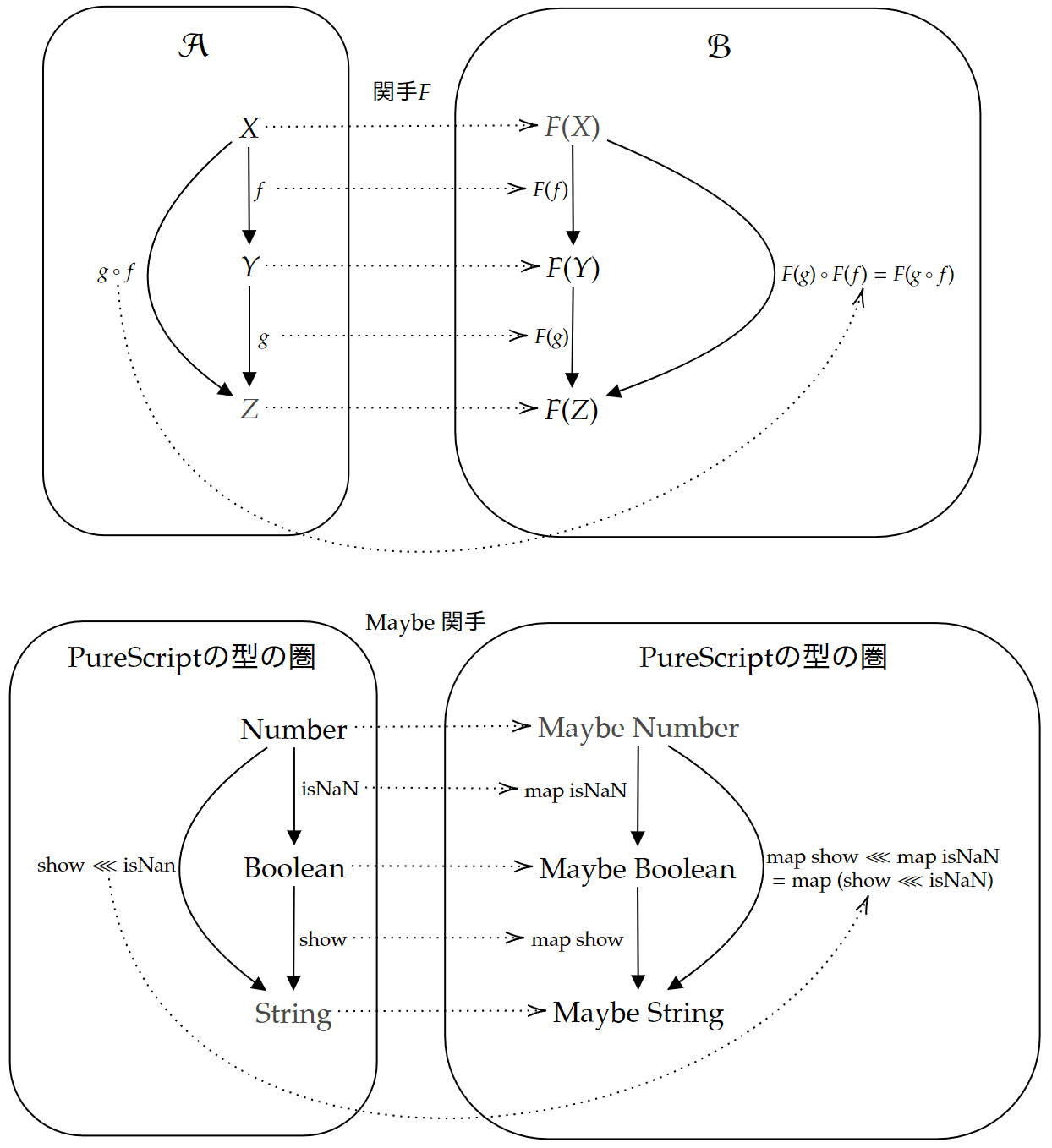
自然変換

続いて、重要な概念である自然変換を見ていきます。

【定義】自然変換

${\footnotesize \mathcal{A} ,\mathcal{B}}$ を圏とし、${\footnotesize F:\mathcal{A\rightarrow B} ,\ G:\mathcal{A\rightarrow B}}$を関手とする。
自然変換 ${\footnotesize \alpha :F\rightarrow G}$ とは、${\footnotesize \mathcal{B}}$ の射の族 ${\footnotesize \left( \alpha _{X} :F( X)\rightarrow G( X)\right)_{X\in \mathcal{A}} }$ であって
${\footnotesize \mathcal{A}}$ の各射 ${\footnotesize f:X\rightarrow Y}$ について、図式

が可換になるものをいう。

また ${\footnotesize \alpha_{X}}$ や ${\footnotesize \alpha_{Y}}$ を自然変換${\footnotesize \alpha}$の成分と呼ぶ。

上記の図式を対象とその間の射まで書いたもの

${\footnotesize \alpha}$ が ${\footnotesize F}$ から ${\footnotesize G}$への自然変換であることを表すのに次のように書くこともある。

定義としては圏・関手の次に登場した自然変換ですが、書籍『ベーシック圏論』には

実際のところ, 自然変換なる概念を定式化したいという要求が圏論を誕生させた. 1940年代初頭, 代数的位相幾何学者「自然変換」という言い回しを, あくまで非公式に使い始めた. 正確な定義の必要性を見抜いたのが, Samuel Eilenberg と Saunders Mac Lane という二名の数学者である. しかし, 自然変換を定義するには関手を定義する必要があり, そして関手を定義するには圏を定義する必要があった. このようにして圏論は誕生した.
(Tom Leinster. (2014) "Basic Category Theory". (斎藤 恭司 監修, 土岡 俊介 訳. (2017)『ベーシック圏論 普遍性からの速習コース』))

と書かれており、実は登場順は逆だったようです。

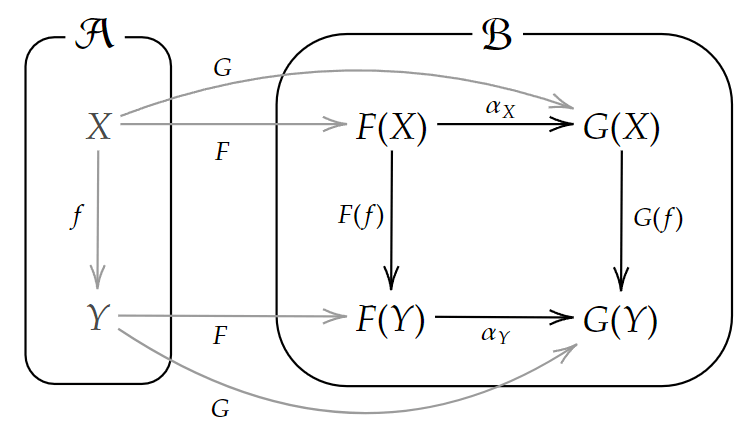
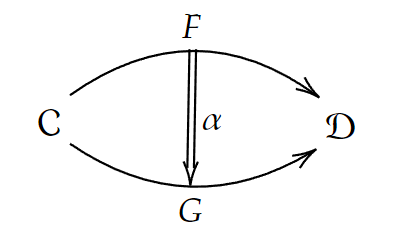
【定義】恒等変換

射に対して恒等射が定められ、関手に対して恒等関手が定められたように、自然変換に対して恒等変換(恒等自然変換ともいう)が定められる。


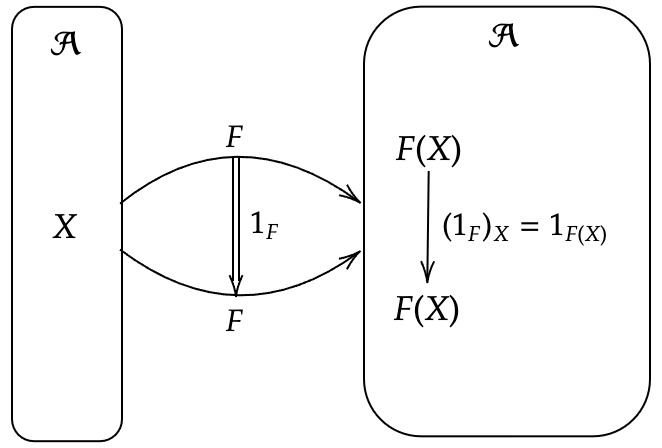
恒等変換の図式

対象とその間の射まで書いた図式

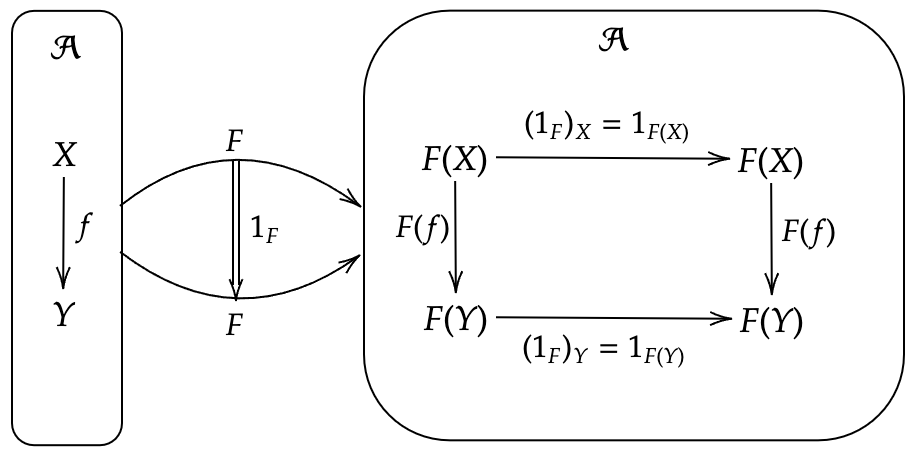
自然変換の合成

自然変換は射の一種なので、合成できる。
そして自然変換の合成には次のような合成の仕方がある。

• 垂直合成
• 水平合成
  • 関手との水平合成
  • 恒等変換との水平合成

順番にこれらの合成を見ていこう。

垂直合成

与えられた自然変換

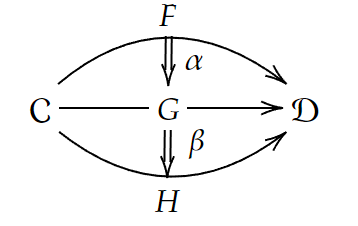
について、合成された自然変換

が、${\footnotesize X\in \mathcal{C}}$について${\footnotesize ( \beta \circ \alpha )_{X} =\beta _{X} \circ \alpha _{X}}$と定義される。
この合成を垂直合成という。

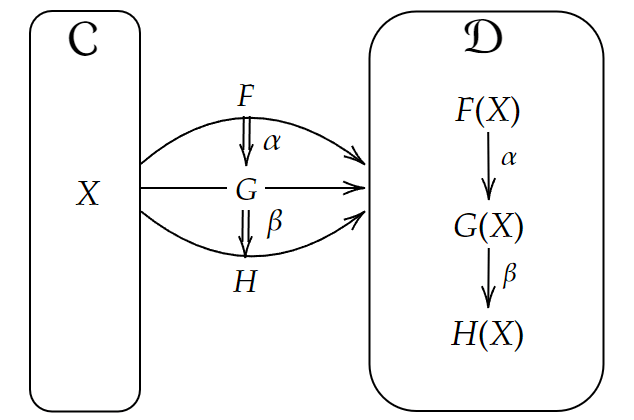
図式

対象とその間の射まで書いた図式

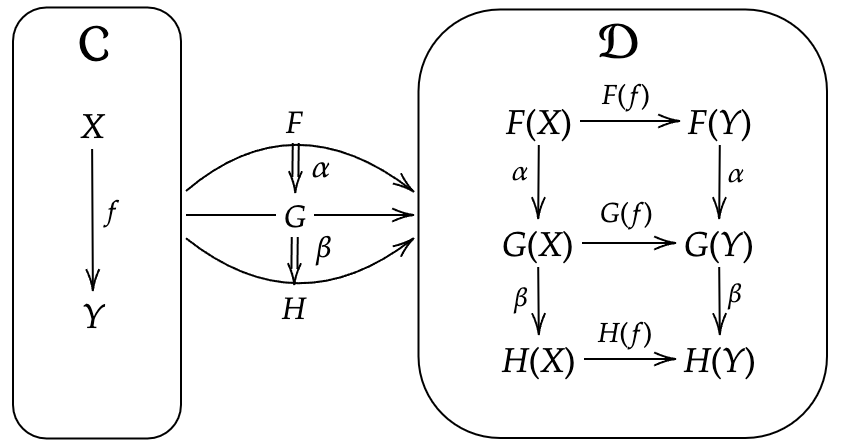
水平合成

垂直合成に対して水平合成もある。それは自然変換

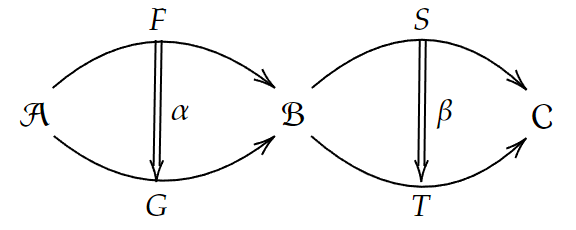
を受け取り、自然変換

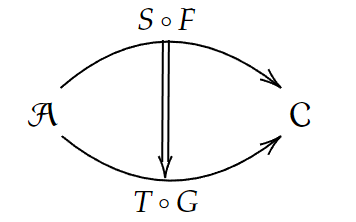
を作り出す。これを${\footnotesize 𝛽*𝛼}$と書く。

自然変換の水平合成の表記は${\footnotesize 𝛽*𝛼}$の他に${\footnotesize 𝛽\circ 𝛼}$や${\footnotesize 𝛽𝛼}$や${\footnotesize 𝛽\cdotp 𝛼}$などがある。
紛らわしい表記を避けるため、この記事では${\footnotesize 𝛽*𝛼}$を採用する。

${\footnotesize X\in \mathcal{A}}$における${\footnotesize \beta *\alpha }$の成分は、自然性図式

の対角線として定義される。
言い換えると、${\footnotesize ( \beta *\alpha )_{X}}$は${\footnotesize \beta _{G( X)} \circ S( \alpha _{X})}$または${\footnotesize T( \alpha _{X}) \circ \beta _{F( X)}}$として定義される。これらは等しいからどちらを採用しても違いはない。

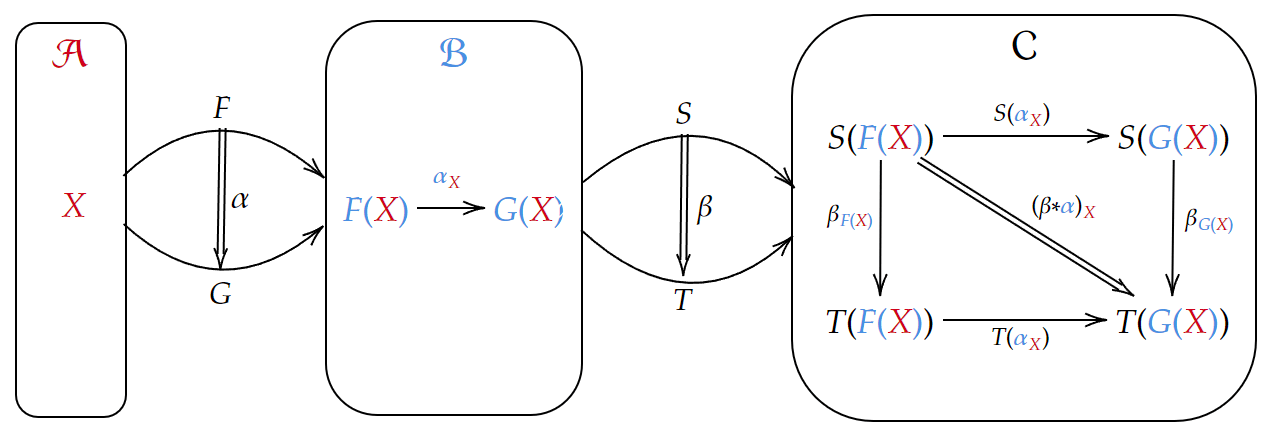
図:上記の水平合成を色分けして圏と対象まで描いた図式

対象とその間の射まで書いた図式

恒等変換との水平合成

水平合成の特別な場合に、自然変換と恒等変換の合成がある。
これはとりわけ重要で、それ専用の記法がある。たとえば

• 自然変換 ${\footnotesize \alpha:G\rightarrow H}$
• 恒等変換 ${\footnotesize 1_{F}:F\rightarrow F}$
• 関手 ${\footnotesize F:\mathcal{A}\rightarrow \mathcal{B} }$
• 関手 ${\footnotesize G:\mathcal{B}\rightarrow \mathcal{C} }$
• 関手 ${\footnotesize H:\mathcal{B}\rightarrow \mathcal{C} }$

に対して

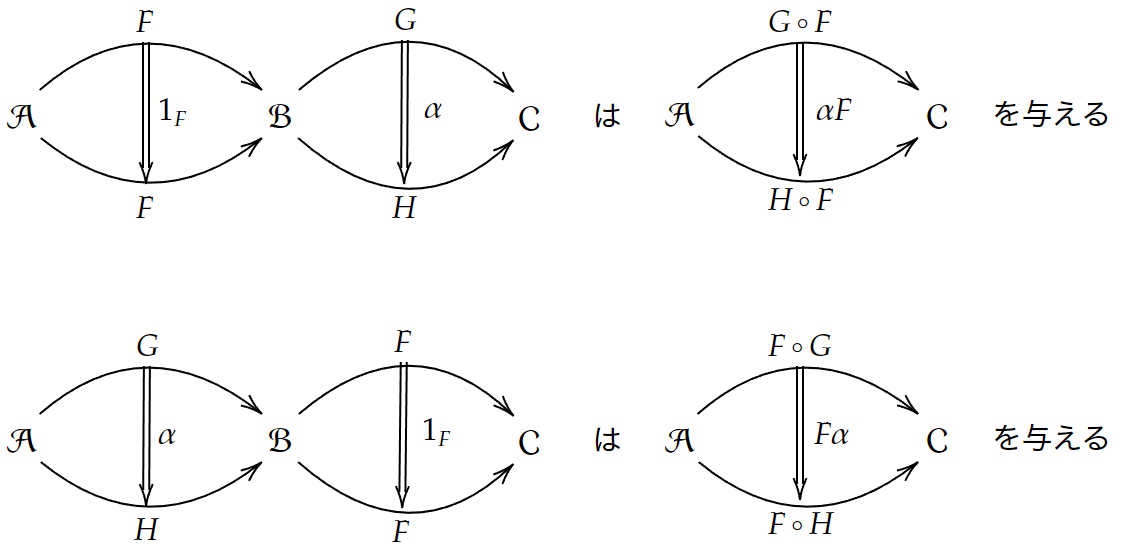
ここで${\footnotesize (\alpha F)_{X} =\alpha _{F(X)}}$かつ${\footnotesize ( F\alpha )_{X} =F( \alpha _{X})}$である。

---

これらの水平合成を図式にしてみます。
まず${\footnotesize ( \alpha F)_{X} =\alpha _{F(X)}}$です。

図式

対象とその間の射まで書いた図式

${\footnotesize \mathcal{C}}$の可換図式において2つの自然変換の垂直合成${\footnotesize \alpha _{F(X)} \circ 1_{G(F(X))}}$および${\footnotesize 1_{H(F(X))} \circ \alpha _{F(X)}}$はどちらも恒等変換を含んでおり、${\footnotesize \alpha _{F( X)}}$とみなせます。

次は${\footnotesize ( F\alpha )_{X} =F( \alpha _{X})}$です。

図式

対象とその間の射まで書いた図式

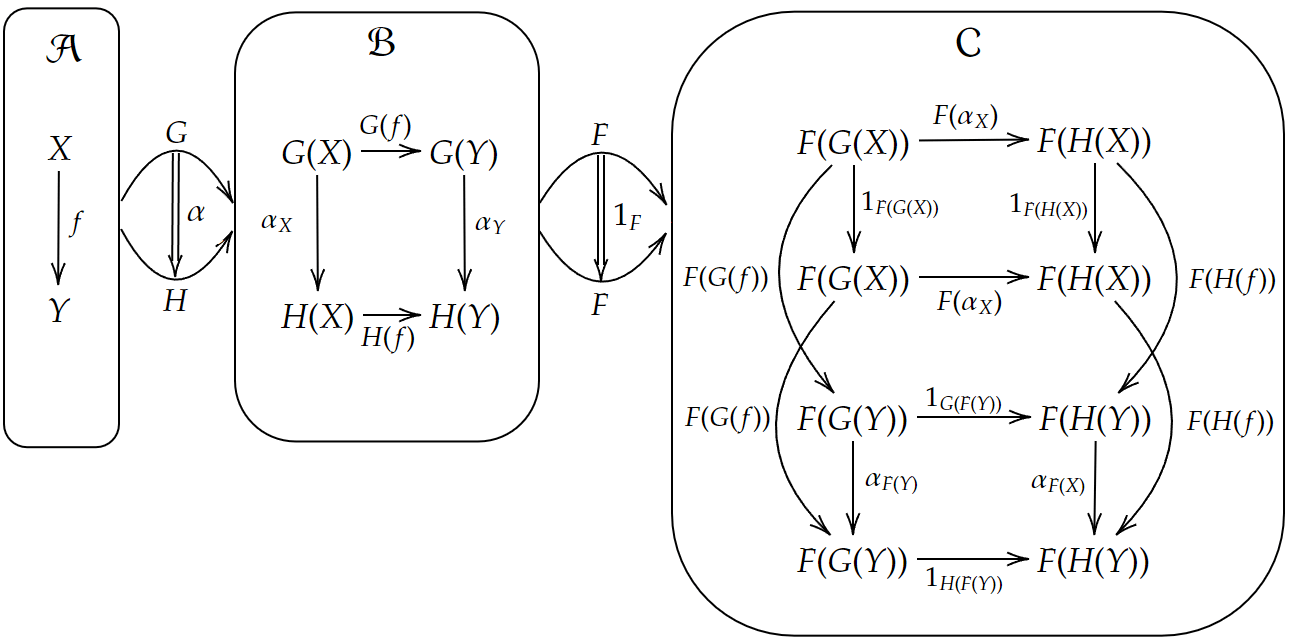
こちらも${\footnotesize \alpha _{F( X)}}$と同様に、圏${\footnotesize \mathcal{C}}$における垂直合成は恒等変換を含んでおり、これも結局のところ${\footnotesize F( \alpha _{X})}$とみなせます。

関手との水平合成

自然変換は関手と合成することもできる。

• 自然変換 ${\footnotesize \alpha:G\rightarrow H}$
• 関手 ${\footnotesize F:\mathcal{A}\rightarrow \mathcal{B} }$
• 関手 ${\footnotesize G:\mathcal{B}\rightarrow \mathcal{C} }$
• 関手 ${\footnotesize H:\mathcal{B}\rightarrow \mathcal{C} }$

があったとして、自然変換${\footnotesize \alpha}$と関手${\footnotesize F}$の合成${\footnotesize \alpha F}$は次のようになる。


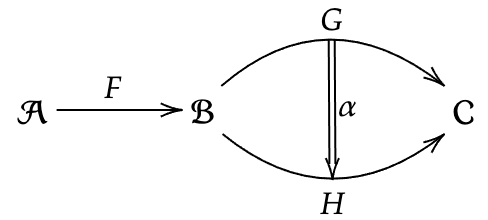
図式

対象とその間の射まで書いた図式

また、${\footnotesize F \alpha }$は次のようになる。


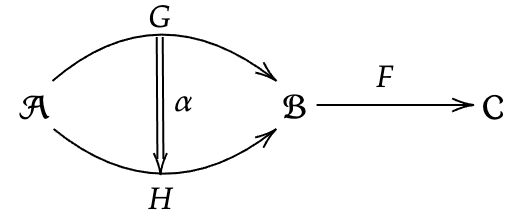
図式

対象とその間の射まで書いた図式

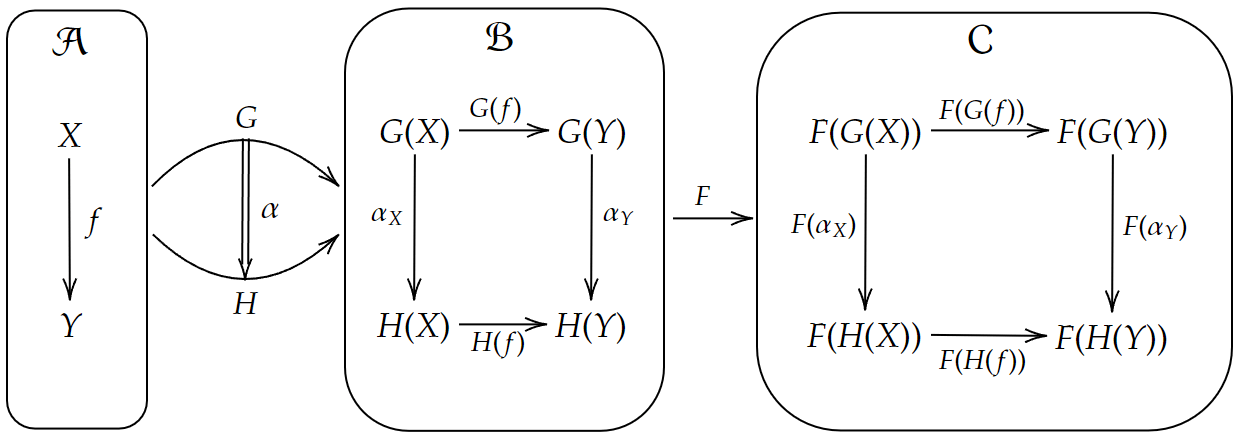
このような関手と自然変換の合成はwhiskeringと呼ばれる。
関手を恒等変換と同一視するならば、whiskeringは水平合成の特殊な場合である。

対象とその恒等射を同一視することができるということを考えるならば、
関手というのはいわば自然変換にとっての対象なわけなので、同じ理屈で関手と恒等変換を同一視できることがわかるかと思います。
実際に「恒等変換と自然変換の水平合成」の項と見比べていただくと、両者の${\footnotesize \alpha _{F( X)}}$と${\footnotesize F(\alpha _{X})}$は同一視できることがお分かりいただけると思います。
この合成は後ほどモナドの定義で再登場します。

whiskerは「ヒゲ」を意味する。ニュッと横に伸びた関手の部分がヒゲっぽいからでしょうか。
日本語では「ヒゲ結合」と書かれるようです。

PureScriptの自然変換

PureScriptにおいては自然変換は次のように定義されています。

Data.NaturalTransformation

type NaturalTransformation :: forall k. (k -> Type) -> (k -> Type) -> Type
type NaturalTransformation f g = forall a. f a -> g a

infixr 4 type NaturalTransformation as ~>

fからgへの自然変換はf ~> gと表すことができます。
ここで着目したいのは上記の定義のどこにも圏論の関手に対応するFunctorが出てこないことです。

なぜか説明しましょう。

まず関手には対象に対する対象関数と射に対する射関数がありました。
例えば関手${\footnotesize F}$における対象関数は${\footnotesize A\rightarrow F(A)}$のように対象${\footnotesize A}$を${\footnotesize F(A)}$に写し、同様に関手${\footnotesize G}$における対象関数は${\footnotesize A}$を${\footnotesize G(A)}$に写します。
そして${\footnotesize F(A)\rightarrow G(A)}$のようにそれぞれで写された対象から対象への関数が自然変換なのでした。

では、いま書いた例を${\footnotesize f(a)\rightarrow g(a)}$と小文字にしたらどうでしょう？
PureScriptの自然変換NaturalTransformationの定義f a -> g aと一致しますね。
更にf aやg aという定義には見覚えがあります。
そう、型構築子です。MaybeではMaybe aという定義になっていました。
この型構築子は対象関数に対応するものなので、意味合い的にPureScriptのf a -> g aの定義が自然変換だというのは一定納得できるものなのではないでしょうか。
恐らくFunctorが出てこないのは、Functorに定義されているmap関数は射関数にあたるもので、このNaturalTransformationを定義する上で制約が必須ではなかったからでしょう。

可換性の検証

具体的なFunctorとしてArrayとMaybe、関数として次の2つを用いて可換性を検証してみます。

• head :: forall a. Array a -> Maybe a
• null :: String -> Boolean

headの定義を見ると、これは自然変換とみなせることがわかるでしょう。
nullは射関数map nullとして使います。
図式としてはこんな感じです。処理としては文字列の配列の先頭が空文字かどうか判定するような処理ですね。

検証するテストコードとして次のようなコードを書いてみました。

Test.Main

module Test.Main where

import Prelude

import Data.Array (head)
import Data.String (null)
import Effect (Effect)
import Effect.Aff (launchAff_)
import Test.Spec (describe, it)
import Test.Spec.Assertions (shouldEqual)
import Test.Spec.Reporter (consoleReporter)
import Test.Spec.Runner (runSpec)

main :: Effect Unit
main = launchAff_ $ runSpec [consoleReporter] do
  describe "自然変換は可換である" do
    let
      nt_map = head <<< map null -- mapした後に自然変換
      map_nt = map null <<< head -- 自然変換した後にmap
    it "先頭が空文字の場合" do
      nt_map ["", "any"] `shouldEqual` map_nt ["", "any"]

    it "先頭が空文字でない場合" do
      nt_map ["any", ""] `shouldEqual` map_nt ["any", ""]

実行結果

自然変換は可換である
  ✓︎ 先頭が空文字の場合
  ✓︎ 先頭が空文字でない場合

モナド

長い道のりでしたが、ようやくモナドまでやってまいりました。

【定義】モナド

${\footnotesize \mathcal{C}}$が圏のとき、${\footnotesize \mathcal{C}}$上のモナドは

• 自己関手 ${\footnotesize T:\mathcal{C}\rightarrow \mathcal{C}}$
• 自然変換 ${\footnotesize \eta :1_{\mathcal{C}}\rightarrow T}$
• 自然変換 ${\footnotesize \mu :T^{2}\rightarrow T}$ (${\footnotesize T^{2}}$ は ${\footnotesize T\circ T:\mathcal{C}\rightarrow \mathcal{C} }$ を表す)

の3つ組 ${\footnotesize (T,\eta,\mu)}$ からなり次の条件を満たす。

1. ${\footnotesize \mu \circ T \mu=\mu \circ \mu T}$
2. ${\footnotesize \mu \circ \eta T = 1_{T} = \mu \circ T \eta}$

図式

条件1は結合律を表し、左の図式の可換性に関係します。
条件2は単位元律を表し、右の図式の可換性に関係します。

---

ここで ${\footnotesize T\mu, \mu{T}, T\eta, \eta{T}}$ は、自然変換${\footnotesize \mu, \eta}$と関手${\footnotesize T}$の水平合成です。
(「関手との水平合成」の項で説明した通り、関手とその関手に対応する恒等変換は同一視できるので恒等変換との合成と考えてもいいのですが、よりシンプルに図式が書けるのでここでは関手との合成としました)
自然変換と関手の水平合成は自然変換になので、${\footnotesize \mu \circ T \mu}$などは「自然変換と関手を水平合成してできた自然変換」と自然変換の垂直合成ということですね。

さて、自然変換${\footnotesize \alpha F, F\alpha}$の${\footnotesize A}$成分は、${\footnotesize (\alpha F)_{A} =\alpha _{F(A)}, ( F\alpha )_{A} =F( \alpha _{A})}$でした。
ここから上記の条件と図式は次のように表すことができます。

1. ${\footnotesize \mu_{A} \circ T(\mu_{A}) = \mu_{A} \circ \mu_{T( A)}}$
2. ${\footnotesize \mu_{A} \circ \eta_{T(A)} = 1_{T(A)} = \mu_{A} \circ T(\eta_{A})}$
   
   図式

---

次に冗長かもしれませんが、いくつか補足しておきます。

【補足】モナドの定義に登場する自然変換について

${\footnotesize T( \mu _{A})}$ と ${\footnotesize \mu _{T( A)}}$ の違い

これはどちらも ${\footnotesize T( T( T( A)))}$ から ${\footnotesize T( T( A))}$への射です。それを説明します。

• ${\footnotesize T(\mu _{A})}$:
  自然変換${\footnotesize \mu}$の${\footnotesize A}$成分である射${\footnotesize \mu_{A}:T(T(A))\rightarrow T(A)}$を関手${\footnotesize T}$で写してやると以下の射が得られます。
  (${\footnotesize \mu_{A}}$は関数なのでこの場合の${\footnotesize T}$は射関数である)
  
  $${\footnotesize T( \mu _{A}) :T( T( T( A)))\rightarrow T( T( A))}$$
  
  
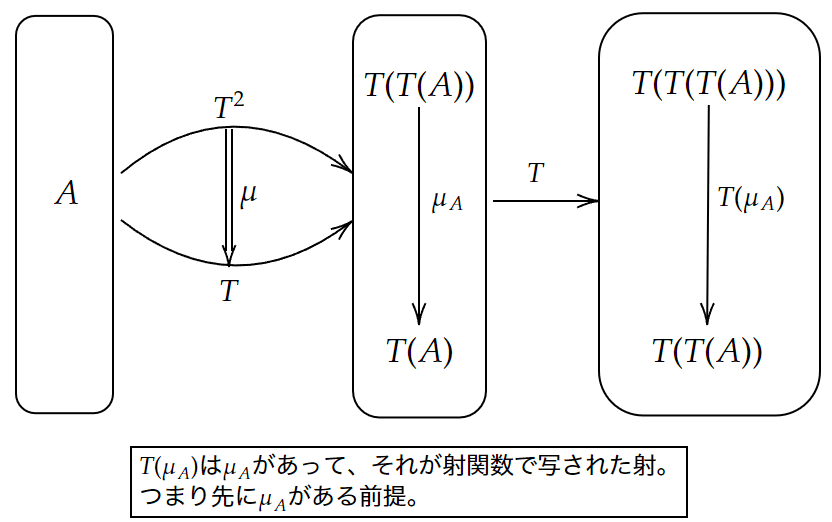
  図式
• ${\footnotesize \mu _{T( A)}}$:
  これは${\footnotesize T(A)}$を一つの塊として考えた自然変換${\footnotesize \mu}$の${\footnotesize T(A)}$成分です。
  つまり${\footnotesize T(T(A)) \rightarrow T(A)}$の${\footnotesize A}$を${\footnotesize T(A)}$で置き換えてやると以下が得られます。
  
  $${\footnotesize \mu _{T( A)} :T( T( T( A)))\rightarrow T( T( A))}$$
  
  
  図式

${\footnotesize T(\eta_{A})}$ と ${\footnotesize \eta_{T( A)}}$ の違い

これはどちらも${\footnotesize T(A)}$から${\footnotesize T(T(A))}$への射です。それを説明します。

• ${\footnotesize T(\eta_{A})}$:
  自然変換${\footnotesize \eta}$の${\footnotesize A}$成分である射${\footnotesize \eta_{A}:A\rightarrow T(A)}$を関手${\footnotesize T}$で写してやると以下の射が得られます。
  
  $${\footnotesize T(\eta_{A}):T(A)\rightarrow T(T(A))}$$
  
  
  図式
• ${\footnotesize \eta_{T(A)}}$
  これは${\footnotesize T(A)}$を一つの塊と考えた自然変換${\footnotesize \eta}$の${\footnotesize T(A)}$成分です。
  つまり${\footnotesize A \rightarrow T(A)}$の${\footnotesize A}$を${\footnotesize T(A)}$で置き換えてやると以下が得られます。
  
  $${\footnotesize \eta _{T( A)} :T( A)\rightarrow T( T( A))}$$
  
  
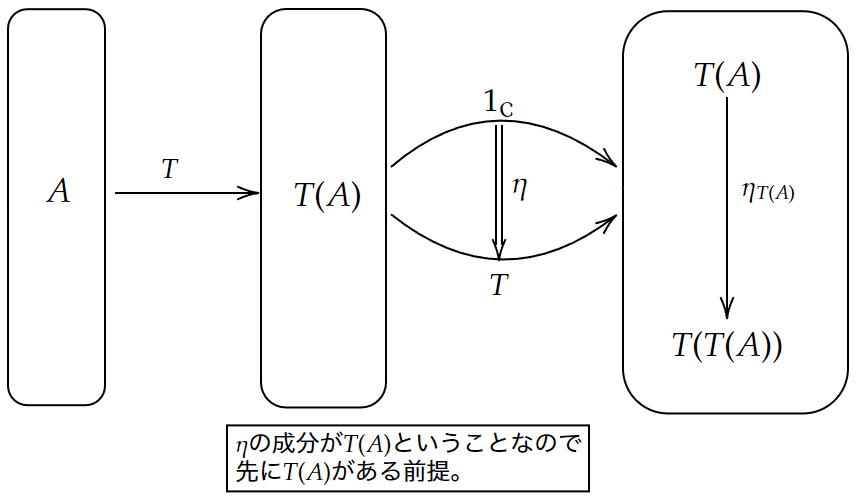
  図式

【補足】単位元律

条件2とは

$${\footnotesize \mu \circ \eta T=1_{T}=\mu \circ T \eta}$$

が成り立つこと、でした。

この条件が意味しているのは、${\footnotesize T}$に対して${\footnotesize \eta}$が先に適用されるか後に適用されるか関わらず、${\footnotesize \mu}$との合成は恒等関手と等しくなければならないということです。

PureScriptのモナド

最後にPureScriptのモナドを見ていきましょう。

PureScriptのモナドの定義

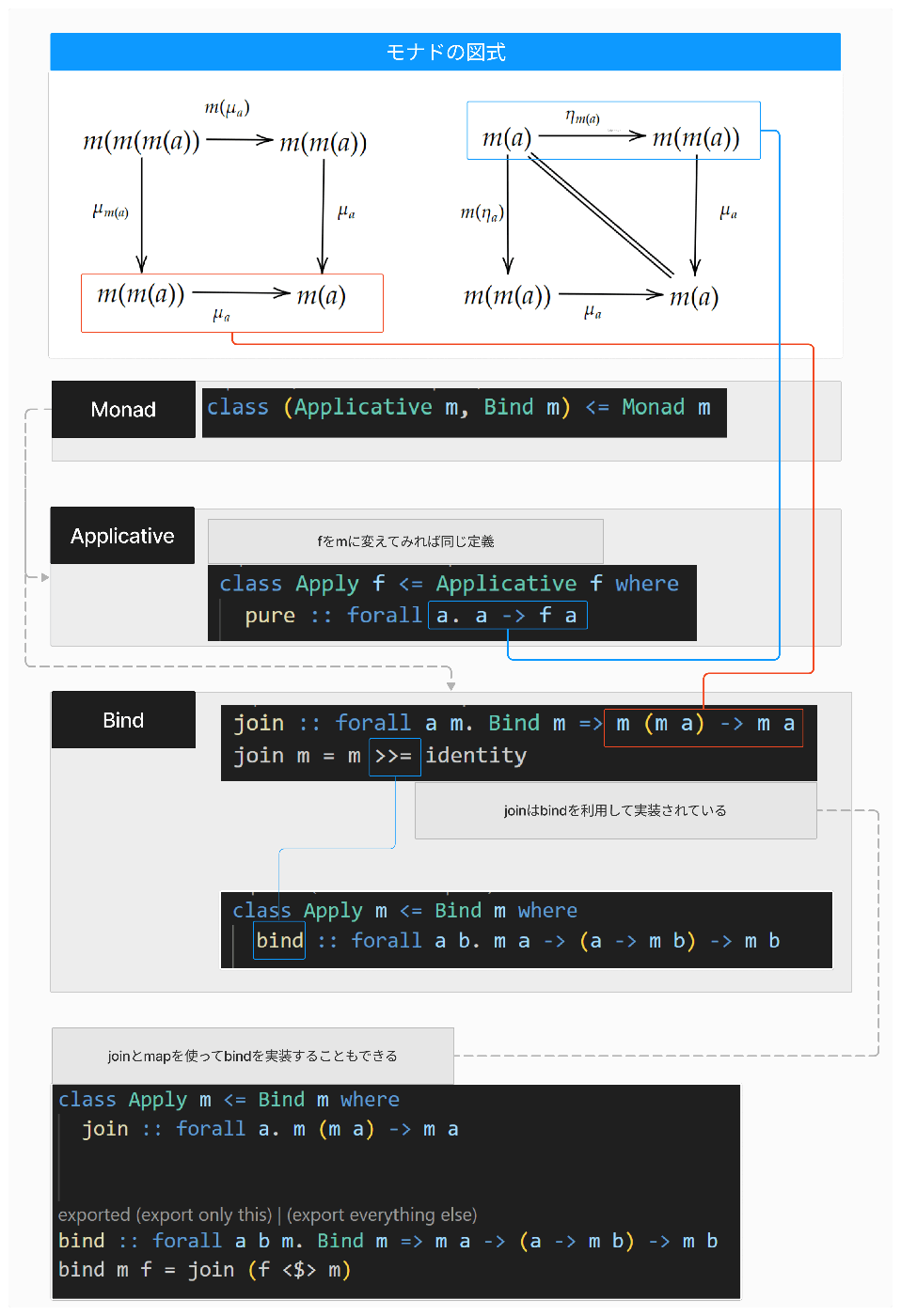
PureScriptのモナドである型クラスMonadは次の定義になっています。

Control.Monad

class (Applicative m, Bind m) <= Monad m

Monadは型クラスApplicativeとBindを継承していますので合わせてこれらを載せておきます。

Control.Applicative

class Apply f <= Applicative f where
  pure :: forall a. a -> f a

Control.Bind

class Apply m <= Bind m where
  bind :: forall a b. m a -> (a -> m b) -> m b

infixl 1 bind as >>=

join :: forall a m. Bind m => m (m a) -> m a
join m = m >>= identity

(joinは後ほど説明で使うので一緒に載せてあります)

自然変換との対応

圏論のモナドには、自己関手${\footnotesize T}$と2つの自然変換${\footnotesize \eta, \mu}$が定義されていました。
これからこの自己関手および2つの自然変換と、PureScriptとの対応を見ていきます。
まず自然変換の方を見ていきます。

自然変換 ${\footnotesize \eta}$

自然変換${\footnotesize \eta}$は${\footnotesize \eta :1_{\mathcal{C}}\rightarrow T}$という定義でした。
これは恒等関手${\footnotesize 1_{\mathcal{C}}}$から関手${\footnotesize T}$への射で、適当な対象${\footnotesize A}$を当てはめると${\footnotesize \eta_{A}:A \rightarrow T(A)}$となります。
上記の関手の名前を${\footnotesize T}$から${\footnotesize f}$に変えて、対象を${\footnotesize a}$とすると

$${\footnotesize \eta_{a}:a\rightarrow f(a)}$$

となります。
ここでPureScriptの型クラスApplicativeの関数pureの定義と見比べてみましょう。

Control.Applicative

class Apply f <= Applicative f where
  pure :: forall a. a -> f a

a -> f aとなっており、形が一致していますね。

${\footnotesize \eta_{a}:a\rightarrow f(a)}\\{\footnotesize \mathrm{pure} :: a \rightarrow f\,a}$

つまり自然変換${\footnotesize \eta}$に対応するのはpureというわけですね。

自然変換 ${\footnotesize \mu}$

自然変換${\footnotesize \mu}$は${\footnotesize \mu :T^{2}\rightarrow T}$という定義でした。
適当な対象${\footnotesize A}$を当てはめると${\footnotesize \mu_{A}:T(T(A))\rightarrow T(A)}$となります。
上記の関手の名前を${\footnotesize T}$から${\footnotesize m}$に変えて、対象を${\footnotesize a}$とすると

$${\footnotesize \mu_{a}:m(m(a))\rightarrow m(a)}$$

となります。
ここでPureScriptの型クラスBindを見てみます。

Control.Bind

class Apply m <= Bind m where
  bind :: forall a b. m a -> (a -> m b) -> m b

bindという関数が定義されていますが、${\footnotesize \mu}$の定義とは合いません。

${\footnotesize \mu}$に対応する関数は、同じモジュールに定義されているjoin関数です。
こちらを${\footnotesize \mu}$の定義と見比べてみましょう。

Control.Bind

join :: forall a m. Bind m => m (m a) -> m a
join m = m >>= identity

形が一致していますね。
${\footnotesize \mu_{a}:m(m(a))\rightarrow m(a)}\\{\footnotesize \mathrm{join} :: m(m\,a) \rightarrow m\,a}$

joinの実装を見るとbindとの関係性がわかります。

join m = m >>= identity

>>=は次のように演算子のエイリアスとして宣言されています。つまりjoinはbindを使って実装されています。

infixl 1 bind as >>=

このようにjoinはbindを利用して実装されていますが、逆にjoinを使ってbindを実装することができます。

joinを使ってbindを実装する例

まず型クラスBindにbindではなくjoinを定義します。

class Apply m <= Bind m where
  join :: forall a. m (m a) -> m a

joinを使ってbindを実装するにはこのようにすればよいでしょう。

bind :: forall a b m. Bind m => m a -> (a -> m b) -> m b
bind m f = join (f <$> m)

<$>を使っているのでFunctorである必要はありますが、joinを使ってbindが実装できることがわかると思います。

まとめると

• 自然変換${\footnotesize \mu}$に対応するのはjoin関数である。
• join関数とbind関数はいずれか一方だけ定義すればもう一方を実装することができる。

という関係になっています。

自己関手Tとの対応

最後に自己関手です。

関手には対象関数と射関数があるので、それぞれ対応を見ていきます。

対象関数との対応

自己関手${\footnotesize T}$の対象関数は、PureScriptのpure関数におけるfやjoin関数におけるmに対応しています。

まずpureの方を確認します。

Control.Applicative

pure :: forall a. a -> f a

自然変換 ${\footnotesize \eta_{A}:A\rightarrow T(A)}$ の ${\footnotesize T}$ を ${\footnotesize f}$ に変え、${\footnotesize A}$ を ${\footnotesize a}$ に変えて、pureの定義と比較してみると

${\footnotesize \eta_{a}:a\rightarrow f(a)} \\ {\footnotesize \mathrm{pure}::a\rightarrow f\,a}$

というように形が一致しました。

次にjoinを確認します。

Control.Bind

join :: forall a. m (m a) -> m a

自然変換 ${\footnotesize \mu_{A}:T(T(A))\rightarrow T(A)}$ の ${\footnotesize T}$ を ${\footnotesize m}$ に置き換え、${\footnotesize A}$ を ${\footnotesize a}$ に置き換えて、joinの定義と比較してみると

${\footnotesize \mu_{a}:m(m(a))\rightarrow m(a)} \\ {\footnotesize \mathrm{join}::m\,(m\,a)\rightarrow m\,a}$

というように形が一致しました。

射関数との対応

関手${\footnotesize T}$の射関数はPureScriptにおいてはmap関数でした。
ということは ${\footnotesize T(\eta_{A})}$ や ${\footnotesize T(\mu_{A})}$ はmap pureやmap joinに対応することになります。

まず ${\footnotesize T(\eta_{A})}$ との対応をみます。
replでmap pureの型を見るとこのように表示されます(見づらいので改行しています)。

> :t map pure
forall (f8 :: Type -> Type) (t11 :: Type -> Type) (t12 :: Type).
  Functor f8 => Applicative t11 => f8 t12 -> f8 (t11 t12)

もうちょっと見やすくするため関手の型をMaybeとしてみます。

> import Data.Maybe
> t = map@Maybe
> η = pure@Maybe
> :t t η
forall (t5 :: Type). Maybe t5 -> Maybe (Maybe t5)

${\footnotesize T(\eta_{A}):T(A)\rightarrow T(T(A))}$ の ${\footnotesize T}$ をMaybeに置き換え、${\footnotesize A}$ を ${\footnotesize t5}$ に置き換えたものと上記を比較してみると

${\footnotesize \mathrm{Maybe}(\eta_{t5}):\mathrm{Maybe}(t5)\rightarrow \mathrm{Maybe}(\mathrm{Maybe}(t5))}\\{\footnotesize t \eta :: \mathrm{Maybe\,t5}\rightarrow \mathrm{Maybe\,(Maybe\,t5)}}$

というように形が一致しました。

次に ${\footnotesize T(\mu_{A})}$ との対応も見ます。
pureと同様に関手の型をMaybeとしreplでmap joinの型を見ると次のように表示されます。

> import Data.Maybe
> t = map@Maybe                                   
> μ = join :: forall a. Maybe (Maybe a) -> Maybe a
> :t t μ
forall (t7 :: Type). Maybe (Maybe (Maybe t7)) -> Maybe (Maybe t7)

${\footnotesize T( \mu _{A}) :T( T( T( A)))\rightarrow T( T( A))}$ の関手名や成分を上記に合わせて置き換えたものと比較すると

${\footnotesize \mathrm{Maybe}(\mu_{t7}):\mathrm{Maybe}(\mathrm{Maybe}(\mathrm{Maybe}(t7)))\rightarrow \mathrm{Maybe}(\mathrm{Maybe}(t7)) }\\{\footnotesize t\,\mu::\mathrm{Maybe}(\mathrm{Maybe}(\mathrm{Maybe}\,t7))\rightarrow \mathrm{Maybe}(\mathrm{Maybe}\,t7)}$

というように形が一致しました。

結合律の検証

結合律${\footnotesize \mu \circ T \mu=\mu \circ \mu T}$を検証してみます。

この条件において自然変換の成分を${\footnotesize A}$とすると
${\footnotesize \mu_{A} \circ T(\mu_{A}) = \mu_{A} \circ \mu_{T( A)}}$
となります。

検証のために具体的な型を与えます。
${\footnotesize A}$はIntとし、関手${\footnotesize T}$はArrayとしますね。
すなわち${\footnotesize T(A)}$はArray Intで、${\footnotesize T(T(T(A))}$はArray (Array (Array Int))となります。

そして ${\footnotesize \mu}$ がjoin関数であることを踏まえると ${\footnotesize \mu _{T(A)}}$ はArray Intに対するjoinなので、Array (Array (Array Int))をArray (Array Int)に写すというjoinになります。つまり単なるjoinです。
一方 ${\footnotesize T(\mu_{A})}$ ですが、この場合の${\footnotesize T}$は射関数なのでmap joinになります。

これで材料が揃いました。
結合律: ${\footnotesize \mu_{A} \circ T(\mu_{A}) = \mu_{A} \circ \mu_{T( A)}}$
に対するPureScriptの擬似コードはjoin <<< map join = join <<< joinとなります。
（=で比較はできませんし、そもそも関数自体の比較ができないのでこれはあくまで擬似コード）

結合律の検証は次の単体テストで行います。具体的な値を与えています。

module Test.Main where

import Prelude

import Effect (Effect)
import Effect.Aff (launchAff_)
import Test.Spec (describe, it)
import Test.Spec.Assertions (shouldEqual)
import Test.Spec.Reporter (consoleReporter)
import Test.Spec.Runner (runSpec)

main :: Effect Unit
main = launchAff_ $ runSpec [consoleReporter] do
  describe "Array Intはモナドの条件を満たす" do
    it "結合律を満たす" do
      let 
        t3 = [
          [
            [1, 2], 
            [3, 4]
          ], [
            [5, 6],
            [7, 8]
          ]
        ]
      (join <<< map join) t3 `shouldEqual` (join <<< join) t3

結果は次の通りです。

結果

Array Intはモナドの条件を満たす
  ✓︎ 結合律を満たす

単位元律の検証

単位元律${\footnotesize \mu \circ \eta T=1_{T}=\mu \circ T \eta}$が成り立つことを検証します。

この条件において自然変換の成分を ${\footnotesize A}$ とすると
${\footnotesize \mu_{A} \circ \eta_{T(A)} = 1_{T(A)} = \mu_{A} \circ T(\eta_{A})}$
となります。

結合律の検証と同じく具体的な型を与えます。

対象${\footnotesize A}$はInt
関手${\footnotesize T}$はArray
とします。
つまり${\footnotesize T(A)}$はArray Intとなります。

自然変換${\footnotesize \mu}$はjoin
自然変換${\footnotesize \eta}$はpure
となります。

したがって
単位元律: ${\footnotesize \mu_{A} \circ \eta_{T(A)} = 1_{T(A)} = \mu_{A} \circ T(\eta_{A})}$
に対するPureScriptの擬似コードはjoin <<< pure = identity = join <<< map pureとなります。

検証のテストコードは次になります。

module Test.Main where

import Prelude

import Data.Maybe (Maybe(..))
import Effect (Effect)
import Effect.Aff (launchAff_)
import Test.Spec (describe, it)
import Test.Spec.Assertions (shouldEqual)
import Test.Spec.Reporter (consoleReporter)
import Test.Spec.Runner (runSpec)

main :: Effect Unit
main = launchAff_ $ runSpec [consoleReporter] do
  describe "Array Intはモナドの条件を満たす" do
    it "単位元律を満たす" do
      let
        ta = [10, 20, 30]
      (join <<< pure) ta `shouldEqual` identity ta
      (join <<< map pure) ta `shouldEqual` identity ta

結果は次の通りです。

Array Intはモナドの条件を満たす
  ✓︎ 単位元律を満たす

おまけ:モナド則の検証

ところでプログラミングにおけるモナドには、モナド則という条件があります。
プログラマーとしてはこちらの方が馴染みがあるかもしれませんね。

このモナド則をPureScriptで表すとこうなるでしょう。

• 左単位元律: pure a >>= h = h a
• 右単位元律: m >>= pure = m
• 結合律: (m >>= g) >>= h = m >>= (\x -> g x >>= h)

このモナド則を検証するテストを書いてみます。
モナドはMaybeとしました。

Test

module Test.Main where

import Prelude

import Data.Maybe (Maybe(..))
import Effect (Effect)
import Effect.Aff (launchAff_)
import Test.Spec (describe, it)
import Test.Spec.Assertions (shouldEqual)
import Test.Spec.Reporter (consoleReporter)
import Test.Spec.Runner (runSpec)

main :: Effect Unit
main = launchAff_ $ runSpec [consoleReporter] do
  describe "Maybeはモナド則を満たす" do
    it "左単位元律を満たす" do
      -- `pure a >>= h = h a`
      let h = Just
      (pure 10 >>= h) `shouldEqual` h 10
    
    it "右単位元律を満たす" do
      -- `m >>= pure = m`
      let m = Just 10
      (m >>= pure) `shouldEqual` m
    
    it "結合律を満たす" do
      -- (m >>= g) >>= h = m >>= (\x -> g x >>= h)
      let
        m = Just 1
        g = \x -> pure (x + 10)
        h = \x -> pure (show x)
      ((m >>= g) >>= h) `shouldEqual` (m >>= (\x -> g x >>= h))

まとめ

おわりに

圏論とPureScriptとの繋がりを見てきましたが、いかがでしたか。
私自身はこのようにバックグラウンドにある理論との繋がりが見える言語は面白いなと感じました。

圏論との繋がりという意味では、まだ他にも面白そうなテーマがあるので、また機会があれば書いてみたいと思います。

参考資料

参考にさせていただいた書籍およびWeb上の資料です。

• ベーシック圏論 普遍性からの速習コース - Tom Leinster (著), 斎藤 恭司 (監修), 土岡 俊介 (翻訳)
  定義は書籍を参照したかったため購入
• ゆる圏 YouTube - @yuruken
  書籍『ベーシック圏論』を読む際、参考にさせていただきました。
• 圏と関手 【 圏論とモナド #1 / 数学 解説 】 - 豊穣ミノリ
  豊穣ミノリ / Hojo Minori さんの一連の動画です(この続きもあります)。視覚的にわかりやすく、ざっくり理解するのに助かりました。
• 自然変換・関手圏 - alg-d
  壱大整域で有名なalg-dさんのテキストです。動画も投稿されており、拝見しました。
• 関手と自然変換の計算に出てくる演算子記号とか - 檜山正幸
  これまた有名な檜山正幸さんが圏論の演算子記号について書かれた記事です。