罰則項付きSynthetic Control法

前回の続き：https://zenn.dev/falconnnmmm/articles/ecf333ba18b2f7

今回はAbadie et al. (2021)で提案された手法"A Penalized Synthetic Control" (罰則付き合成コントロール法)について解説していきます。

モチベーションと定式化

基本的な設定や記号は前回と同様とします。
この論文のモチベーションは 集計前のデータ (disaggregated data) に対してsynthetic controlを適用するための方法を提示することにあります。Part 1で紹介した方法、および応用先は国レベルや州レベルなどで集計 (aggregate) されたデータを対象としていますが、もう少し細かいレベルでデータが見れるならそのレベルで推定したほうがバイアスが減らせるはずです。

例えばPart 1で紹介したカリフォルニア州にタバコ税を導入したことによるタバコの売上への影響はカリフォルニア州全体で見ていますが、元々のデータは小売店単位で売上が発生していて、それをどんどん集計したものをデータとして見ています。しかしカリフォルニア州の中でもサンフランシスコとロサンゼルスでは影響の大きさが異なるかもしれません。

集計前のデータでsynthetic controlを考える場合、処置を受ける人が複数存在しうることになります。ですが考え方は同じで、各処置群の人に対してアウトカムをコントロール群のアウトカムの加重平均で再現することを考えます。このときweightは処置を受ける人によって異なると考えます。
これを数式で表現すると次のようになります。

• $i=1,2,\cdots,N$: unit
  • 処置群は $n_{1}$ 人、コントロール群には $N-n_{1}$ 人存在する
• $\alpha_{i,j}$: 処置群のunit $i$ について コントロール群のunit $j$ に置くweight
• perfect fit assumption: 各 $i=1,\cdots,n_{1}$ に対して以下を満たすweight $\bm{\alpha}_{i}=(\alpha_{i,n_{1}+1},\cdots,\alpha_{i,N})$ が存在する。

$$Y_{it}(0) = \sum_{j=n_{1}+1}^{N}\alpha_{ij}Y_{jt}(0)\\ \alpha_{i,n_{1}+1}\geq 0,\ \cdots,\ \alpha_{i,N} \geq 0\\ \sum_{j=n_{1}+1}^{N}\alpha_{ij} = 1$$

この論文ではweightを求めるための最適化問題を次のように定めています。

$$\min_{\bm{\alpha}_{i}\in\mathbb{R}^{N}} \bigg(Y_{it} - \sum_{j=n_{1}+1}^{N}\alpha_{i,j}Y_{jt}\bigg)^{2} + \lambda \underbrace{\sum_{j=n_{1}+1}^{N}\alpha_{i,j}\big(Y_{it}-Y_{jt}\big)^{2}}_{\text{penalty}} \\ s.t. \ \ \ \ \alpha_{i,j}\geq 0 \ \ (j=n_{1}+1,\cdots,N)\\ \ \ \ \ \sum_{j=n_{1}+1}^{N}\alpha_{i}=1$$

Part 1で紹介した最適化問題と比較すると第2項が追加されていることが分かると思います。$\lambda(>0)$ は罰則の大きさを表すハイパーパラメータで分析をする人が事前に決定するものです。この $\lambda$ を含む項が罰則項(penalty term)となっており、Lidge回帰のような形をしている点が特徴的です。
推定されたweightを使うと処置群一人ひとりに対する処置効果

$$\tau_{it} = Y_{it} - \sum_{i=n_{1}+1}^{N}\widehat{\alpha}_{i,j}Y_{jt}$$

が推定でき、例えば

$$\tau_{t} = \dfrac{1}{n_{1}} \sum_{i=1}^{n_{1}}\tau_{it}$$

は処置群に対する（時刻 $t$ の）集計された平均処置効果となります。

なぜ罰則項が必要なのか

さて、上の最適化問題に罰則項があるわけですが、この項が存在する主な理由は解が一意に定まらない可能性が高いからです。処置群のアウトカムを完全に再現するようなweightの組み合わせが複数ある場合、どのweightの組み合わせが相応しいでしょうか？
重要な点として、処置前のデータではちゃんとperfect fitが達成されているか確認することができますが、処置後のデータでは $Y_{it}(0)$ が再現できているかを確認することができません。つまり複数の組み合わせが解として得られたとして、もっとも"相応しい"ものを選ぶ基準がないことになります。
もしはじめから得られる解（組み合わせ）が一つに定まっていればそのweightを使えばいいので上記の懸念点は払拭されます。この問題を解決する方法が罰則項の存在になります。Abadie et al. (2021)のTheorem 1は上の最適化問題から得られる解は一通りに定まり、かつ疎（変数の数に対して0が多い）になることを示した定理です。

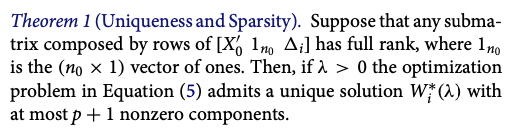
$\lambda$をどのように決めるか

罰則の強さは $\lambda$ の大きさによって決まります。しかしこれは事前に分析する人によって決めておくハイパーパラメータです。$\lambda$ の大きさによって得られる解が変わるのでうまくこれを決めてあげる必要があります。

Leave-One-Out Cross-Validation

ここでは $\lambda$を決める方法としてLeave-One-Out Cross-Validationという方法を紹介します。まず手順を見てみましょう。

1. 各コントロール群 $i=n_{1}+1,\cdots, N$ と処置後の時刻 $t=T_{0}+1,\cdots,T$ に対して以下を求める。ここで $\alpha_{ij}(\lambda)$ は、ある $\lambda$ の下で $i$ を除いたコントロール群で推定したweightである

$$\tau_{it}(\lambda) = Y_{it} - \sum_{j=n_{1}+1,j\neq i}^{N}\alpha_{ij}(\lambda)Y_{jt}$$

2. 様々な $\lambda$ に対して上を求めたら、各 $\lambda$ に対して2乗予測誤差

$$\sum_{i=n_{1}+1}^{N}\sum_{t=T_{0}+1}^{T} \big(\tau_{it}(\lambda)\big)^{2}$$

を求め、それを最小にするような $\lambda$ を求める

何をやっているかと言うと、コントロール群のデータから1人分だけのデータを除いて推定して、その人のアウトカムとの誤差を最小にするように $\lambda$ を選べばよいという方法になっています。コントロール群のデータであれば、要は「答え」が分かっているので予測の精度を調べることができます。

応用例：

今回はAbadie et al. (2021)の応用例を題材とします^[1]。

（手元でうまく再現できないので後日更新します）

参考文献

Abadie, A., Diamond, A., & Hainmueller, J. (2010). Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. Journal of the American statistical Association, 105(490), 493-505.

脚注

1. 前回の応用例は処置を受けたunitが1つしかないですが、今回は複数いるパターンです。