📝
Synthetic Control法 (合成コントロール法)

2024/03/11に公開
因果推論
 これはなに？因果推論の手法であるSynthetic Control法（合成コントロール法）とは何か？についてまとめたもの
簡単な理論の説明とその応用について記述する
出来れば因果推論の基本的な用語（処置、処置効果、コントロール群など）は所与のものとさせてください。

あと何か間違いなどがあればコメントください。よろしくお願いします。

 設定簡単にnotationだけ定義しておきます。

i: unit （個人、国など）

t: 時刻

T_{0}: 処置が行われる時刻。影響が出るのは T_{0} よりも後の時間とする

Y_{it}: 時刻 t におけるunit i のデータから観測されたアウトカム (observed outcome)

Y_{it}(d_{it}): 時刻 t におけるunit i の処置状態が d_{it} である場合のpotential outcome

 Synthetic Control法（合成コントロール法）とは？
 基本的な考え方Synthetic Control法（合成コントロール法）とは因果推論において因果効果を推定するための手法ですが、処置を受ける人が1人しかいないときに有効な手法となります。

因果推論でよく見られる状況は、処置群とコントロール群にそれぞれ複数の人がいて、グループ間でアウトカムの差を調べるというものでしょう。

より具体的に説明するためにすでにnotationで定義していますが、改めて Y_{it} を時刻 t で観測された i さんのアウトカムとします。そして d_{it} はその時刻における i さんの処置状態を表すものとします。つまり d_{it}=1 なら i さんは処置群の人、 d_{it}=0 なら i さんはコントロール群の人を表します。この d_{it} を使って potential outcome (潜在アウトカム) を Y_{it}(d_{it}) と表すことにします。例えば Y_{it}(1) は i さんが処置群だった場合のアウトカムを表します[1]。

例えば因果推論の黄金律とも言えるRCTで処置効果を推定するときは

\mathbb{E}[Y_{it}(1)] - \mathbb{E}[Y_{it}(0)]
によって平均処置効果(ATE)が計算できます。RCTであればcounterfactual outcomeも識別可能です。
しかし処置群が1人（以下ではi=0という人が処置を受けたとします）という状況で知りたいのは、単純な処置効果

\tau_{t} = Y_{0t}(1) - Y_{0t}(0)
です。これは個別処置効果(individual treatment effect; ITE)とも呼ばれます。Y_{0t}(1) は 0 さんが時刻 t において処置を受けている場合のアウトカムで、これはデータから観測されます（observed outcomeと呼びます)。そして Y_{0t}(0) がデータから観測できない、反実仮想のアウトカムになります。これ自体はたとえRCTでも推定できません。
イメージとしては以下のような感じです。青線が 0 さんのデータから観測されたアウトカム、赤線は処置が起きなかった世界のアウトカムです。青線と赤線の差が上記の処置効果に該当します。

当然ですが、この赤線は実際のデータでは観測できないので、このままでは処置効果を推定することもできません。


synthetic controlが対象とするデータの例。データで見えるのは青線。赤線は別の世界線のアウトカム
そこでAbadie et al. (2010)では以下の仮定を置きました。
各時刻 t=1,2,\cdots,T において以下の等式を満たすようなweight  (\alpha_{1},\cdots,\alpha_{N}) が存在する。

Y_{0t}(0) = \sum_{i=1}^{N}\alpha_{i}Y_{it}(0)
この仮定はperfect fitの仮定と呼ばれます。つまり、「処置を受けていない世界の 0 さんのアウトカムは、実際に処置を受けていないコントロール群の人のアウトカムを加重平均したもので表すことができる」という仮定です。
上図の灰色がデータから観測されたコントロール群の人たちのアウトカムとします。perfect fitの仮定はこの灰色の線(上図では10人分あります）にそれぞれweightを置くことで、本来は観測できないはずの Y_{0t}(0) (t>T_{0}) を再現しようという内容になります。
perfect fitの仮定により、処置効果が次のように識別可能（つまりデータから推定ができる状態）となります。

\tau_{t} = Y_{0t}(1) - Y_{0t}(0) = Y_{0t}(1) - \sum_{i=1}^{N}\alpha_{i}Y_{it}(0)
したがって\alpha_{1},\cdots,\alpha_{N}を求めることが処置効果を推定するための鍵となるわけです。

 推定方法ではどうやってweightを推定するのかという話ですが、処置が起きる前、すなわちt\leq T_{0}のデータからY_{0t}(0)を観測することができるので、t\leq T_{0}のデータを使って以下の式からweightを推定します。

Y_{0t} = \sum_{i=1}^{N}\alpha_{i}Y_{it} + \varepsilon_{t}, \ \ (t=1,2,\cdots,T_{0})
これを見るとOLSで推定すればよさそうに見えます。しかし、後で実践例で見るようにOLSだと過学習を起こす可能性があります。

Abadie et al (2010)など多くのsynthetic controlに関する研究ではweightは以下の最適化問題の解として得られるものとしています。

\widehat{\bm{\alpha}} = \arg\min_{\alpha\in\mathbb{R}^{N}} \big(Y_{0t} - \sum_{i=1}^{N}\alpha_{i}Y_{it}\big)^{2},\\
s.t.\ \ \ \ \alpha_{i} \geq 0, \ \ (i=1,2,\cdots,N)\\
\ \ \ \ \sum_{i=1}^{N}\alpha_{i}=1
制約付き最小化問題の解として定式化されるため、通常のOLSを使うことはできません。しかし、これも後で実践例で見ますが、結果としてperfect fitを達成するために必要なコントロール群の人を"選択"するような問題となっているため、Synthetic Controlでは広く使われている定式化です。なお、perfect fitを仮定しているので、処置前の時刻ではどの時刻でも Y_{0t}-\sum_{i=1}^{N}\alpha_{i}Y_{it} は 0 となっていることが望ましいですが、実用上は平均二乗誤差(MSE)

\dfrac{1}{T_{0}}\sum_{t=1}^{T_{0}}\big(Y_{0t} - \sum_{i=1}^{N}\alpha_{i}Y_{it}\big)^{2}
を目的関数とする最適化問題を解くことによってweightを推定します。

なお、Abadie et al. (2010)では関心のあるアウトカム Y_{it} だけでなく、その他の共変量も加えて

\widehat{\bm{\alpha}} = \arg\min_{\alpha\in\mathbb{R}^{N}} \|\bm{X}_{0t}-\bm{X}_{t}\bm{\alpha}\|,\\
s.t.\ \ \ \ \alpha_{i} \geq 0, \ \ (i=1,2,\cdots,N)\\
\ \ \ \ \sum_{i=1}^{N}\alpha_{i}=1
のほうが予測力が強くなると言及しています。ここで \bm{X}_{0} は k行のベクトル、\bm{X}は k\times N の行列で、k が共変量の数です。

 使い道合成コントロール法は「処置を受けた人が一人だけ」という状況さえ用意できればかなり応用範囲が広い（とくにビジネス面で有効な）手法だと思います。ここから先に挙げる例以外に、ビジネス的な観点から見れば「ある企業が商品の価格を値上げした。このことが売上に与える影響はどの程度だったか？」という命題に対しては、他社の値上げをしていない、似たような商品（同じジャンルなど）の売上データがあれば合成コントロール法を使うことができます。個別の売上データが難しい場合は企業レベルで分析しても面白いかもしれません。

 応用例1: Abadie et al. (2010)Abadie et al. (2010)では1988年にカリフォルニア州で導入されたタバコ税が、州内のタバコの売上にどのような影響を与えたか分析しています。

タバコ税が導入されたのはカリフォルニア州だけなのでsynthetic controlの出番です。コントロール群はアメリカ50州のうち、38州です。12州はデータの観測期間にタバコ税を導入していたり、既に導入済みだが、タバコ税を引き上げたりした州です。


Abadie et al. (2010) Figure 3

"Proposition 99"がカリフォルニア州におけるタバコ税の導入です。上図の点線が推定によって得られた（別世界の）カリフォルニアにおけるタバコの売上になります。処置前のfitが少しずれているように見えるのが気になりますが、概ねよく再現できているように見えます[2]。
この結果からタバコ税を導入したことで売上がかなり下がったことが示唆されます。タバコに税金を導入→タバコが値上げする→買い控えが起きるというメカニズムになっている考えられるため、かなり直感的な結果になっているのではないでしょうか[3]。

 応用例2: Abadie et al. (2015)こちらの論文は1990年の東西ドイツ統一というイベントによって西ドイツの（一人あたり）GDPにどのような影響を与えたのか推定したものになります。当然ですが、国家の統一・合併というイベントが同じタイミングに複数箇所で起きることはまあないので、これもまたsynthetic controlの出番になります。この推定ではコントロール群としてOECD諸国を利用しています。


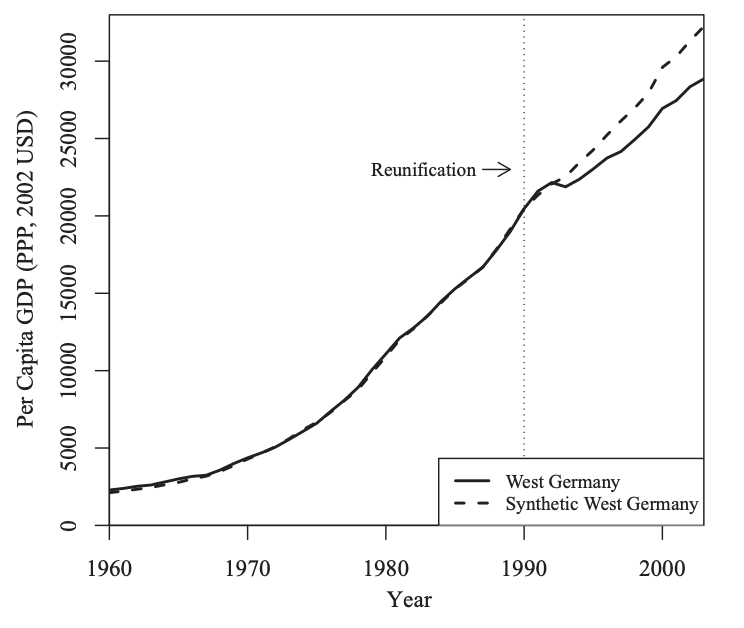
Abadie et al. (2015) Figure 2

点線が「統一が起きなかった世界の西ドイツ」のGDPなので、東西ドイツの統一というイベントは西ドイツに対して負の影響を与えていることが示唆されます。

この論文ではこの結果に対してスピルオーバーが存在する可能性を指摘し、結果の頑健性について色々と検証しています。興味がある方は読んでみてください。

 実践せっかく理論を紹介したので、実際にsynthetic control法を体感してみましょう。

今回使うデータは応用例1で紹介したAbadie et al. (2010)よりタバコの売上データです。"Causal Inference: The Mixtape" (邦訳あり)の著者であるScott CunninghamがGithub上でデータを公開しているので、それを使います。
今回はPythonで実装していきます。なお、筆者はPandasよりもPolarsが好きなので、最初のデータフレーム読み込みだけPandasを使いますが、基本的にはPolarsで書いていきます。

 データ# 必要なライブラリ
import pandas as pd
import polars as pl
from scipy.optimize import minimize
import plotly.graph_objects as go # 可視化

# データの読み込み
# 拡張子が.dta (Stataファイル)なのでread_stata関数を使う
df = pd.read_stata('./data/smoking.dta')
df = pl.from_pandas(df)

T = len(df['year'].unique()) # 観測された時間の長さ
N = len(df['state'].unique()) - 1 # control unitの数
T0 = 1988 - 1970 + 1 # 処置が始まるまでの時間

df.head()



state
year
cigsale
lnincome
beer
age15to24
retprice


0
Alabama
1970
89.8
nan
nan
0.178862
39.6

1
Alabama
1971
95.4
nan
nan
0.179928
42.7

2
Alabama
1972
101.1
9.49848
nan
0.180994
42.3

3
Alabama
1973
102.9
9.55011
nan
0.18206
42.1

4
Alabama
1974
108.2
9.53716
nan
0.183126
43.1

これを見ると6つの列があるlong形式のデータフレームですが、Abadie et al. (2010)によれば使った変数は"cigsale" (タバコ1パックあたりの売上)と"retprice" (小売店の販売価格)だそうなので、"state", "year", "cigsale", "retprice"だけ残します[4]。
次にデータをpivotテーブルにして処置前の期間のデータと処置後の期間のデータに分割します。Proposition 99は1988年11月に成立したので、T_{0}=1988 として
pre-treatment period: 1970 ~ 1988
post-treatment period: 1989 ~ 2000
とします。

以下のコードは必要なデータを作るための作業ですが、何をしたいのかイメージを貼っておきます。



これはコントロール群のデータ(X)のイメージですが、やりたいことは処置群のデータも同じです。

このようにデータを作ることで

\underset{2T_{0}\times 1}{\bm{Y}} = \underset{2T_{0}\times N}{\bm{X}}\underset{N\times 1}{\bm{\alpha}} + \underset{2T_{0}\times 1}{\bm{\varepsilon}}
という式でweightが推定できます。
df = pd.read_stata('./data/smoking.dta')
df = pl.from_pandas(df)

T = len(df['year'].unique()) # 観測された時間の長さ
N = len(df['state'].unique()) - 1 # control unitの数
T0 = 1988 - 1970 + 1 # 処置が始まるまでの時間

# print(df.head().to_pandas().to_markdown())
df = df.select(
    "state", "year", "cigsale", "retprice"
)

# X: N×T0*2 matrix
X = df.filter(
(pl.col("state") != "California")
& (pl.col("year") <= 1988)
).sort('year')[['cigsale', 'retprice']].to_numpy().T.reshape(N, -1)

Y = df.filter(
    (pl.col("state") == "California")
    & (pl.col("year") <= 1988)
)[['cigsale', 'retprice']].to_numpy().T.reshape(2*T0)
これで推定に必要なデータが準備できました。

 OLSによる推定まずはOLSで推定した場合にどのような結果が出てくるか見てみましょう。

ライブラリを使ってもいいですが、OLSなのでストレートにOLS推定量を出してしまいましょう：

\widehat{\alpha}_{OLS} = \bigg(\bm{X}^{\top}\bm{X}\bigg)^{-1}\bm{X}^{\top}\bm{Y}
で与えられます。
# OLS
alpha_OLS = np.linalg.inv(X.T @ X) @ X.T @ Y
print(alpha_OLS.round(3))
print(alpha_OLS.sum())
weightの推定結果
[-0.618 -0.918  0.633  0.276  0.263  0.958  0.168  0.303 -0.331 -0.099
 -0.578  0.957 -0.356  0.278 -0.03  -0.455 -0.164 -0.621 -0.175 -0.077
  0.079  0.382 -0.326  0.419  0.216 -0.125 -0.1    0.21  -0.398  0.734
  0.315 -0.058  0.504 -0.21  -0.767  0.737  0.026 -0.099]
色々なところにweightが置かれていますね。その大きさも負だったり正だったり、総和が約0.95という結果になっています。

これを使ってfittingの結果だけを見てみましょう。


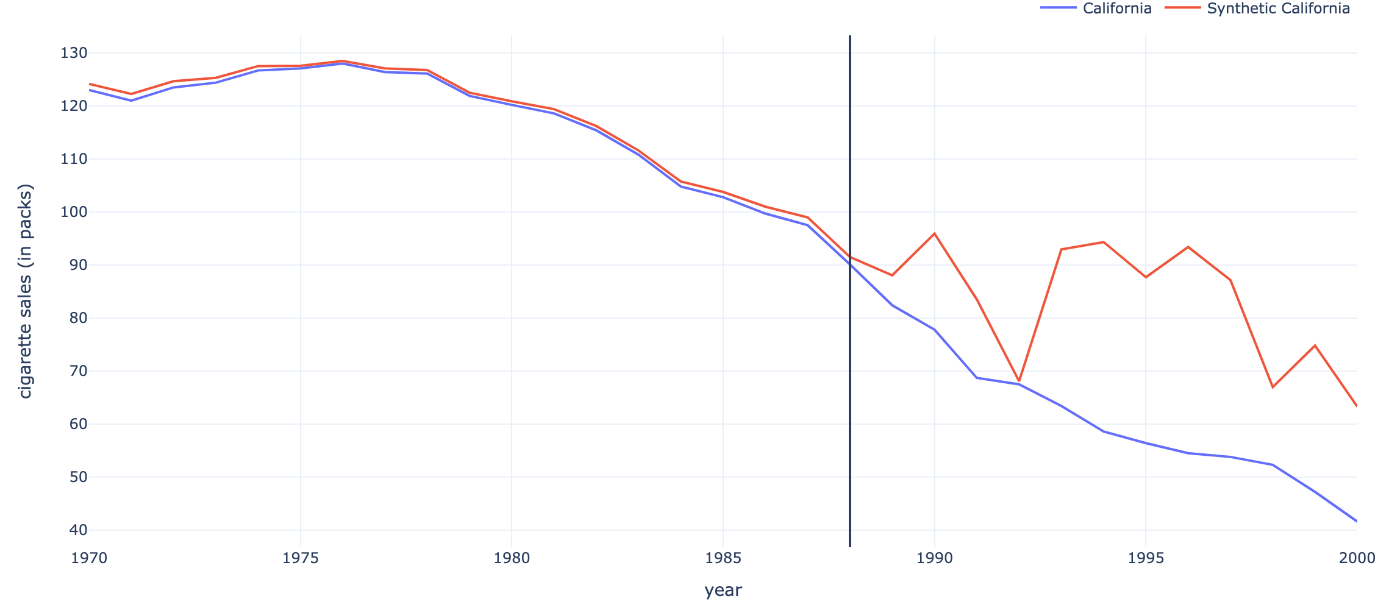
OLSによるcounterfactual outcomeの推定結果

pre-treatment期間のfitは非常に良いように見えます。

しかし処置が行われた後の時間（上図の黒い縦線より右側）を見ると、なんかジグザグしているように見えます。これは推定がoverfitting、過学習をしている可能性が考えられます。

つまり、推定に使ったデータから「出来るだけ完璧に当てはまるように（=perfect fitを達成するように）」weightを推定したはいいが、out-of-sampleの予測にはあまり適していないということです。

 Synthetic Controlによる推定次にSynthetic Controlによる推定をしていきましょう。

基本的にはscipyのメソッドを使って制約付き最小化問題を定義し、その解を求めることになります。
# MSE(平均二乗誤差)を損失関数として、その最小化をする
def loss_function(w, X, y):
    return np.mean((y - X @ w)**2)

cons = (
    {'type': 'eq', 'fun': lambda x: np.sum(x) - 1}
)
bounds = [(0, None) for i in range(N)]

alpha_init = np.ones(N) / N
scm = minimize(
    loss_function,
    x0=alpha_init,
    args=(X, Y),
    constraints=cons,
    bounds=bounds,
    method="SLSQP"
)
alpha_scm = scm.x
print(alpha_scm.round(4))
print(alpha_scm.sum())
weightの推定結果
[0.    0.    0.    0.085 0.    0.    0.    0.    0.    0.    0.    0.
 0.    0.    0.    0.    0.    0.    0.    0.113 0.105 0.457 0.    0.
 0.    0.    0.    0.    0.    0.    0.    0.    0.24  0.    0.    0.
 0.    0.   ]
weightを比較してみましょう。



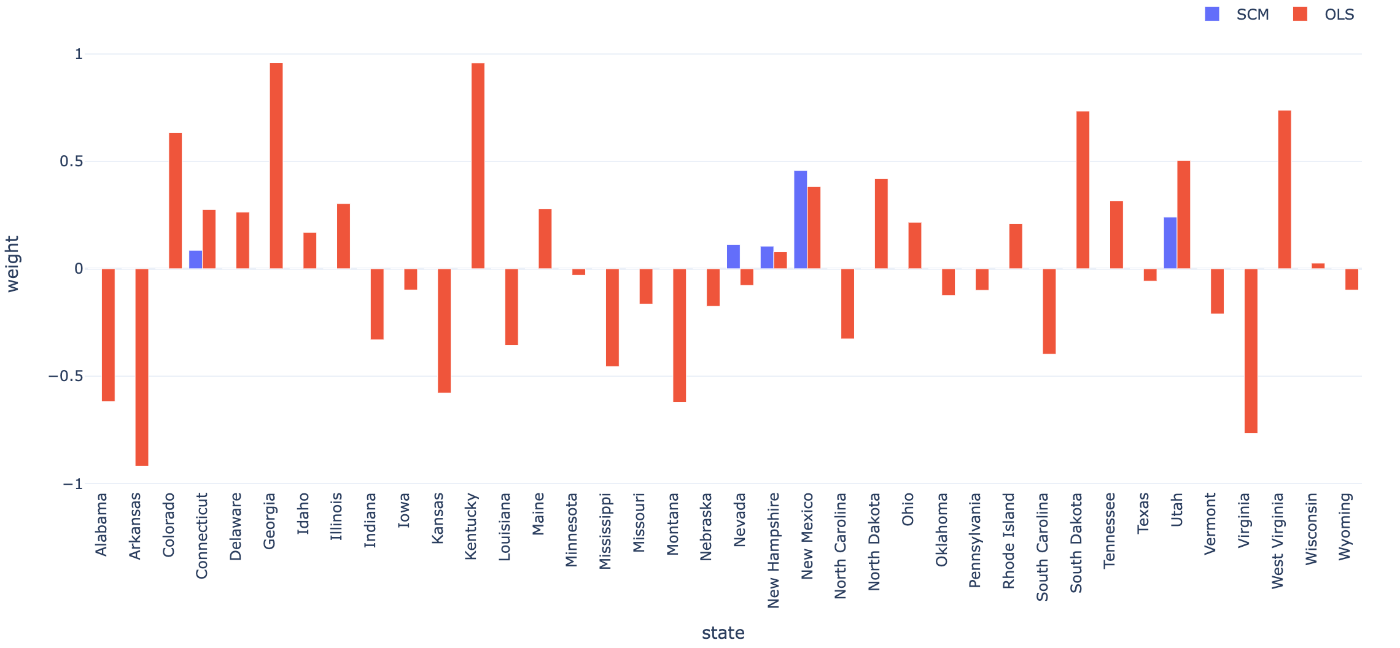
weightの推定結果の比較

青がSynthetic Controlで推定されたweight、赤がOLSで推定されたweightです。

このように見比べると、Synthetic Controlの場合はweightを置く州が非常に少ないことが分かると思います。すなわちweightが疎(sparse)になることが特徴です。weight自体は解釈し辛いものですが、以下の図を見てください。



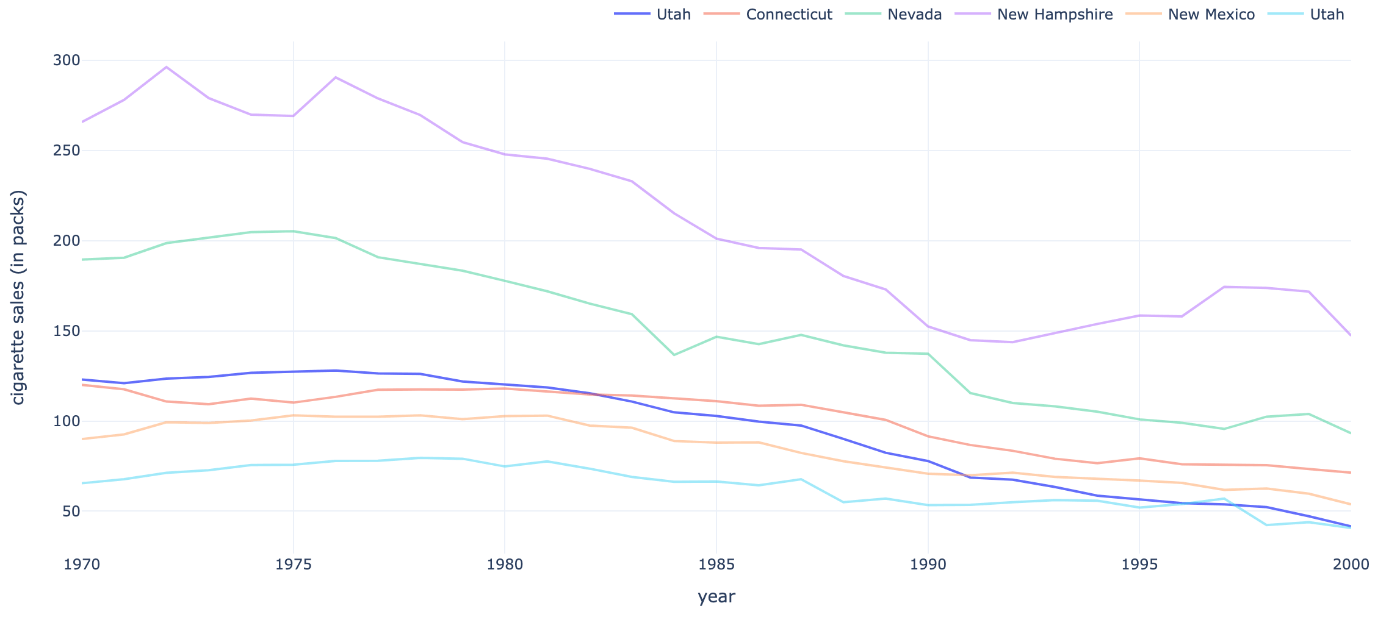
Synthetic Controlで推定されたweightが正の州とカリフォルニア州におけるアウトカム

これを見ると、「コントロール群の州のうち、カリフォルニア州と似たような動きをしている州」に対してweightを置いていると推察されます。OLSではこのような傾向が全く見られないので、制約付き最小化問題によりweightを置く州を"選択"した結果と言えます。


Synthetic Controlによるcounterfactual outcomeの推定結果

これを見ると、タバコ税を導入しなかった世界のカリフォルニア州でもタバコの売上自体は減少するが、その下げ幅が小さくなることが分かります。counterfactual outcomeが推定できたので、処置効果

\tau_{t} = Y_{0t}(1) - Y_{0t}(1) = Y_{0t} - \sum_{i=1}^{N}\alpha_{i}Y_{it}
を推定しましょう。



処置効果の推定結果 (OLSとSynthetic Control)

OLSの結果と比較するとSynthetic Controlのほうが一貫した結果になっている印象です[5]。

 おわりに今回は合成コントロール（Synthetic Control）法とは何か？というテーマで、かなり丁寧に記事を書いてみました。この手法について少しでも興味を持っていただければ幸いです。
(3/30 追記)

先日発売された『因果推論: 基礎から機械学習・時系列解析・因果探索を用いた意思決定のアプローチ』を拝読しました。こちらにも合成コントロール法に関する記述がありますが、この手法の背景的な説明がちょっと物足りないように感じました。因果効果が識別できない→perfect fitで代替→weightをどうやって推定する？という流れをこの記事では意識しました。

 参考になるliteratureAbadie, A., Diamond, A., & Hainmueller, J. (2010). Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. Journal of the American statistical Association, 105(490), 493-505.
Abadie, A., Diamond, A., & Hainmueller, J. (2015). Comparative politics and the synthetic control method. American Journal of Political Science, 59(2), 495-510.
Abadie, A., & L’hour, J. (2021). A penalized synthetic control estimator for disaggregated data. Journal of the American Statistical Association, 116(536), 1817-1834.
Arkhangelsky, D., Athey, S., Hirshberg, D. A., Imbens, G. W., & Wager, S. (2021). Synthetic difference-in-differences. American Economic Review, 111(12), 4088-4118.
Gunsilius, F. F. (2023). Distributional synthetic controls. Econometrica, 91(3), 1105-1117.
Kim, S., Lee, C., & Gupta, S. (2020). Bayesian synthetic control methods. Journal of Marketing Research, 57(5), 831-852.
Ferman, B., & Pinto, C. (2021). Synthetic controls with imperfect pretreatment fit. Quantitative Economics, 12(4), 1197-1221.
Chernozhukov, V., Wüthrich, K., & Zhu, Y. (2021). An exact and robust conformal inference method for counterfactual and synthetic controls. Journal of the American Statistical Association, 116(536), 1849-1864.
Cao, J., & Dowd, C. (2019). Estimation and inference for synthetic control methods with spillover effects. arXiv preprint arXiv:1902.07343.

脚注
実はこの時点でSUTVAと呼ばれるものを仮定しています。簡単に言えば、ある処置が行われたとき、その処置の影響はコントロール群に波及しないというもので、この仮定によりiさんの潜在アウトカムが i さんの処置状態 d_{it} のみに依存すると表すことができます。一般にSUTVAを仮定しない場合は \bm{d}_{t}=(d_{1t},\cdots,d_{Nt})\in\mathbb{R}^{N} を全員の処置状態をまとめたベクトルとして Y_{it}(\bm{d_{t}}) が i さんの潜在アウトカムになります。詳しくは第7回の記事で説明する予定です ↩︎
この少し気になる点は推定精度の向上として課題に残ります。後に紹介する方法ではもっとうまくfitするようになります。 ↩︎
考えられる可能性として、「他の州まで買いに行ったのでカリフォルニア州での売上が減少した」や「タバコの値上げがきっかけでタバコをやめる人が増えたのでカリフォルニア州での売上が減少した」が考えられます。この推定ではどのような経路で売上が減少したのかまでは分からない点に注意が必要です。 ↩︎
データを見ると他の変数は欠損が多いことが分かります。 ↩︎
印象論で語っていますが、後の回でも紹介する予定の他の推定方法では似たような動きになるのでOLSが過学習している可能性のほうが高いです ↩︎
	state	year	cigsale	lnincome	beer	age15to24	retprice
0	Alabama	1970	89.8	nan	nan	0.178862	39.6
1	Alabama	1971	95.4	nan	nan	0.179928	42.7
2	Alabama	1972	101.1	9.49848	nan	0.180994	42.3
3	Alabama	1973	102.9	9.55011	nan	0.18206	42.1
4	Alabama	1974	108.2	9.53716	nan	0.183126	43.1
これはなに？

設定

Synthetic Control法（合成コントロール法）とは？

基本的な考え方

推定方法

使い道

応用例1: Abadie et al. (2010)

応用例2: Abadie et al. (2015)

実践

データ

OLSによる推定

Synthetic Controlによる推定

おわりに

参考になるliterature

Discussion
