CUDA PythonによるCUDAプログラミング入門③:行列積の実装
1. はじめに
筆者はGPUプログラミングを学びながら、並行して記事化を行っています。
今回は、ディープラーニングにおけるGPU活用の本丸である、行列積のGPU実装を詳しく解説し、今後のパフォーマンスチューニングのベースケースとしたいと思います。
また、本記事のなかで、演算量の規模やGPUの演算スペック等の表記で用いられるFLOPsの概念についてもふれます。
本記事の流れ
本記事は以下の流れで解説します:
-
- 行列積の基礎
- 行列積とは何か、どう計算するか
- なぜGPUに適しているのか
-
- スレッドのデータへのマッピング
- スレッドの役割分担
- スレッド別のメモリアクセス
-
- 実装
- CUDA Kernelの実装
- CUDA Pythonによる処理全体の実装
- 実行結果と考察
想定読者
- 本記事でも、Pythonコーディングの経験を前提とします
- 前回までの記事の内容(CUDA Pythonの使い方、2次元データマッピング等)は前提とします
2. 行列積の基礎
行列積の演算を簡単におさらいします。少し端折った説明となりますので、必要に応じ他の解説にあたってください。
2.1 行列の表記
行列は数値を二次元に並べたものです。縦方向にM行、横方向にN列の数値が並んだ行列を
といった具合です。なお、縦と横方向の長さが同じ、すなわち
行列のなかの特定の一つの数値のことを要素と呼びます。ある行列Aのi行k列の要素は
となります。このように、行列自体は大文字、行列の要素はその小文字で表現する場合が多く、本記事でも行列及びその要素の表記はこのルールに則ります。
なお、行列は上記のように大きな丸括弧で表示することが多いですが、これだと可視化がやりにくいので、以降は以下のようにシンプルな格子で表示するようにします。

2.2 行列積の計算
行列積(Matrix Multiplication)は、2つの行列から新しい行列を出力します。M×K行列AとK×N行列Bの積を行列Cとすると、Cの以下の式で定義されます
もし数式アレルギーがある方向けに、具体的なコードで示すと以下の具合です
c[i,j] = 0 #初期化
for k in range(K):
c[i,j] += a[i,k] * b[k,j]
ここで、後の計算量の見積もりで使いますが、一つの要素の計算あたり、K回の掛け算とK回の足し算を行うことを理解しておいてください。
なお、積を計算するさい、行列Aの列(横方向)の長さと、行列Bの行(縦方向)の長さが一致している必要があります。また、普通の数値の掛け算と違い、
2.3 なぜ行列積はGPUに向いているか
行列積は各要素の計算を独立して実行できます。例えば要素c[1,2]の計算を行うとき、c[0,2]やc[1,1]といった他の要素の計算結果は不要です。そのため、出力対象の各要素を独立して計算でき、容易に並列化可能です。
加えて、データの再利用回数の観点でもGPUに向いています。何をいっているかというと、前々回の記事で示したとおり、ホスト(CPU)とデバイス(GPU)の間のデータのやり取りは非常に時間がかかります。そのため、一旦デバイスに移送したデータを、できるだけ繰り返し多く使う計算のほうがGPUのメリットがあります。
データの繰り返し利用について詳しく検討してみましょう。ここでは
-
A B 2*N^2 - 計算結果Cをホストに移送:
N^2
となり、合計3*N^2 T_{移送}
となります。
次に、データ転送後に実行する計算回数は、計算する要素が
となります。結局、行列の掛け算をGPUで行う場合の計算時間は
となります。この式をみるとわかるとおり、第一項(データ移送時間)は
2.4 FLOPsとFLOPS
2.3節で、
浮動小数点の演算1回のことを1FLOPと数えます。FLOPとはFloating-point OPerationでそのまま浮動小数点演算の略称です。そして、当然浮動小数点演算は膨大な回数行われるため、その回数は複数形は小文字sをつけて1,000FLOPsとか1M FLOPsといった具合で表示されます。
上記の表記法を用いると、
とうことになります。
ここでややこしいのでですが、FLOPS(←最後は小文字ではなく大文字のS)という単位があります。FLOPSはFloating-point Operation Per Secondで、1秒間あたりの実行FLOP数ということになります。FLOPSはGPUの演算能力を表示するときによく使われ、例えばA100であればfloat演算で19.5T FLOPS、すなわち単精度小数点の演算を1秒あたり19.5兆回(
上記で"理想的には"と書きましたが、実際はGPUの限界のFLOPSを使い切ることは稀で、実際はこの上限のFLOPSより低い演算量である時間が大半になります。これは、例えばホスト⇄デバイスのデータ転送時間等であったり、デバイス内でもメモリと計算コアの間のデータの読み書きなど、メモリとのデータ転送時間が処理がボトルネックになる場合が多いためです。このGPUのFLOPSをできるだけ使い切ることが、GPU計算の最適化で非常に重要になります。
補足: 浮動小数点数
浮動小数点とは、できるだけコンパクトなデータで、とても大きかったり小さかったりする連続値をコンピュータで表現する方法です。具体的には
のように、数値を仮数部(1.23)と指数部(10²)に分けて表現します。ただし、コンピュータで実際に浮動小数点を扱うさいは上記のような10進数ではなく、2進数で表現されていることに留意してください。
浮動小数点にはいくつか規格がありますが、GPU演算(つまりC/C++)でよく使われるのは、軽量だが性能が低い単精度と、データ量が大きいが性能が良い倍精度があります。具体的なスペックは以下のとおりです
単精度(float)
- 32ビット(4バイト)で表現
- 有効数字:約7桁
- 範囲:約±3.4 × 10³⁸
- メモリ節約、処理が速い
倍精度(double)
- 64ビット(8バイト)で表現
- 有効数字:約15桁
- 範囲:約±1.8 × 10³⁰⁸
- 正確、科学技術計算などに用いる
浮動小数点の規格は上記に限らず、他にも複数あります。特に注目したいのは、ディープラーニング向けに新たに設定された企画でしょう。そのなかでもよく使われるのがGoogle Brainが2018年に提唱したBrain floating point(bf16)です。bf16はコンパクトながら、とくに絶対値が小さい数値の精度を維持できる規格で、スペックは以下のとおりです。
bf16 (bfloat16)
- 16ビット(2バイト)で表現
- 有効数字:約2〜3桁
- 範囲:約±3.4 × 10³⁸ (FP32とほぼ同じ範囲)
- メモリ使用量がFP32の半分、処理が速い
この精度の扱いによる効率化も、追って実験等を行ってみたいと思っています。
2.4 行列のメモリへの配置
前記事で解説したとおり、多次元のデータは1次元のメモリに平坦化(flatten)して配置されます。前回のカラー画像は3次元のデータで少し複雑でしたが、行列は二次元データなのでシンプルです。以下に
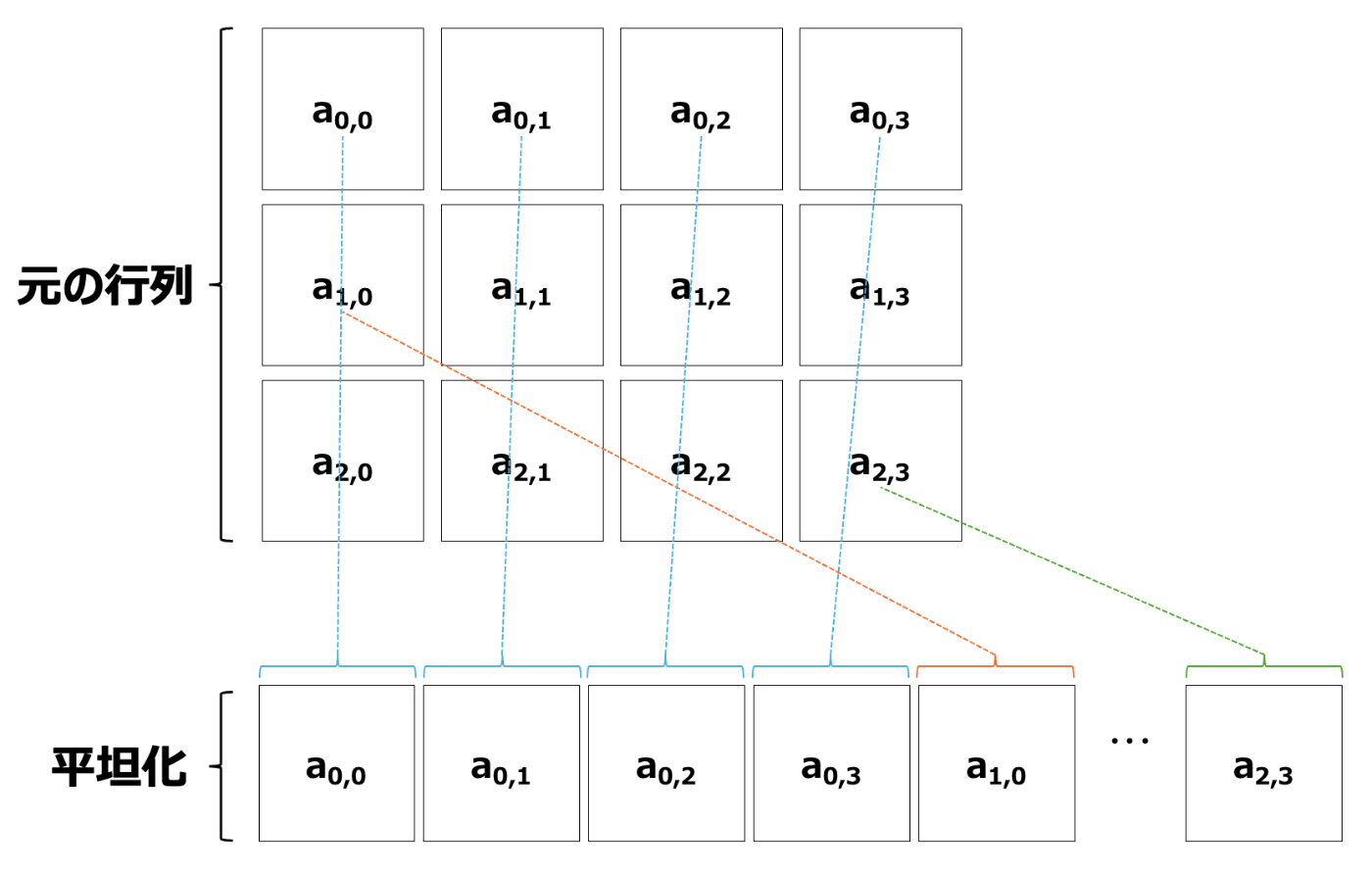
モノクロの画像と同様、まず第0行を並べ、第次に1行、その次に第2行を並べます。
行列についても、Pythonではnumpyのflatten()メソッドにより平坦化が行えます。
3.スレッドのデータへのマッピング
ここまでで行列積の処理内容と、行列をメモリに配置する方法を説明しました。次は処理を並列化して各コアに割り当てるため、スレッドをデータに割り当てる(マッピング)方法を確認します。以下では入力の行列をA(
これまでの記事で繰り返し述べていますが、Kernelを記載するさいは、その計算を行うスレッドの気持ちになることが肝要です。今回は、Kernelは以下を知る必要があります。
- 自分が
Cのどの要素の計算を担当するか - その要素を計算するために、
AおよびBのどの要素をメモリから取ってきて、計算する必要があるのか
以後、順に上記の2点を解説します
3.1 出力Cのどの要素を計算するのか
行列は2次元なので、スレッドがどの要素を扱うのかを割り当てるのは簡単です。以下は前回記事で画像のピクセルをスレッドに割り当てる方法を解説した画像ですが、これと全く同じ方法で行列の要素をスレッドに割り当てることができます。
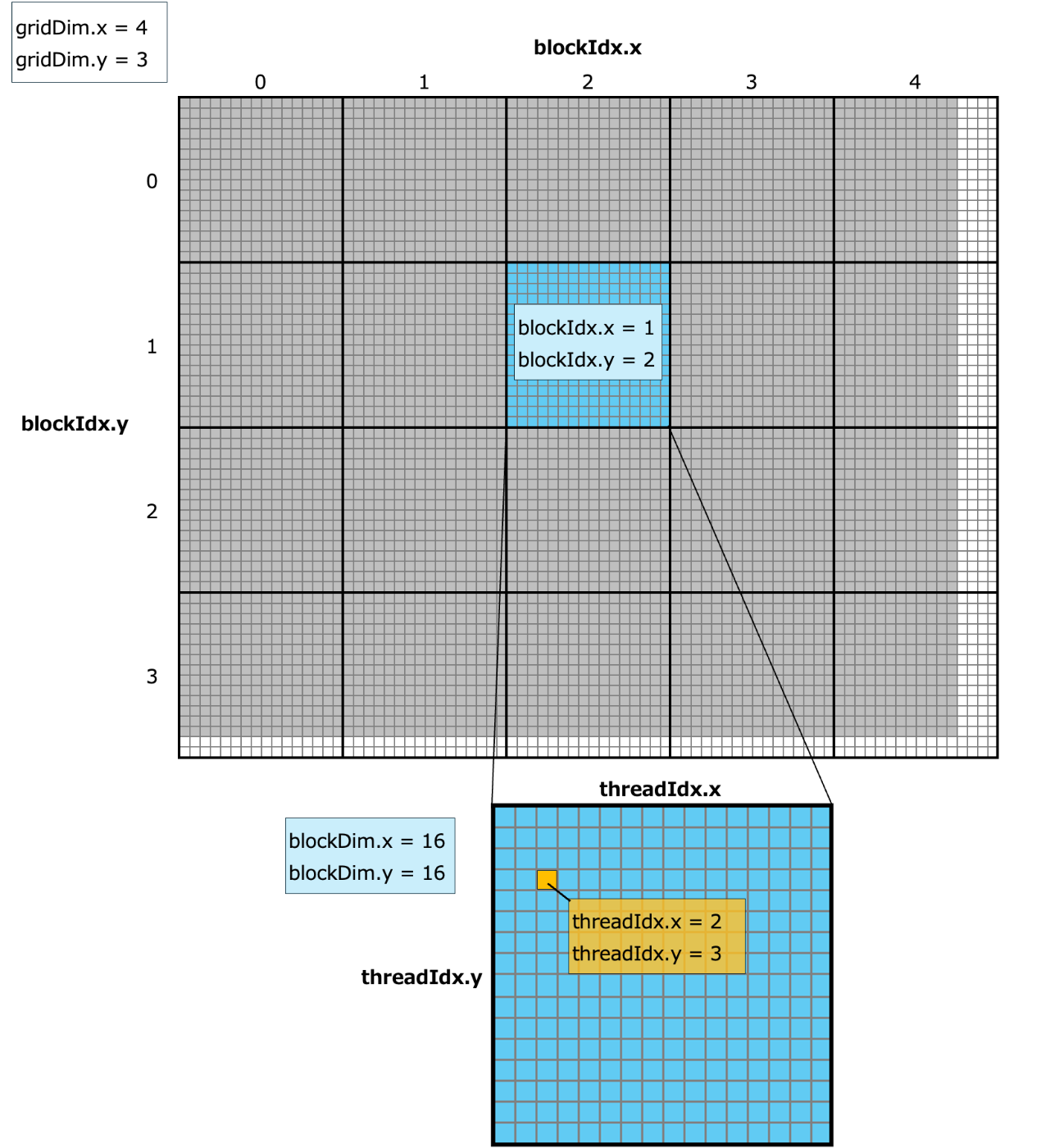
前回記事の3.1節 ブロックとグリッド〜3.4節 境界チェックと全く同じ考え方により割り当てを行うことができます。ただし、画像と行列では、サイズ等の表記方法が縦と横が逆順なので注意してください。
ここでもCを
- 横方向: ceil(N/16)
- 縦方向: ceil(M/16)
のブロックを並べることになります。
次に、各スレッドが処理する対象の要素ですが、要素
row = blockIdx.y*blockDim.y + threadIdx.y
col = blockIdx.x*blockDim.x + threadIdx.x
となります。
また、境界チェックについても
// 境界チェック
if (row < M && col < N) {
・・・(カーネルの処理内容)
}
となります。
3.2 入力A, Bのどの要素を持ってくるのか?
3.1において、スレッドが出力のCのうちのどの要素
2.2節で示したように、
for k in range(K):
c[row,col] += a[row,k] * b[k,col]
となります。そのためa[row,k] およびb[k,col]をメモリから持ってくる必要があります。
前回記事で画像に関して検討したのと同様に、二次元配列において行がrow番、列がcol番の要素は、二次元配列の横幅を
となることを見ました。この式を用いると、まずa[row,k]の平坦化した場合のインデックスは、Aの幅がKであることを用いて
となります。続けてb[k,col]の平坦化した場合のインデックス
となります。
上記をまとめると、for文内の処理はCUDAで以下のように記載すれば良いです。
c += A[row * K + k] * B[k * N + col];
4. 実装
4.1 CUDA Kernelの実装
3.1節と3.2節の検討をふまえると、行列積のCUDA Kernelのナイーブな実装は以下のようになります:
__global__ void matmul(
float *A, float *B, float *C,
int M, int N, int K
) {
// スレッドが計算する出力要素の位置
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
// 境界チェック
if (row < M && col < N) {
float c = 0.0f;
// 要素の計算
for (int k = 0; k < K; k++) {
c += A[row * K + k] * B[k * N + col];
}
// 結果を格納
C[row * N + col] = c;
}
}
以下のrowおよびcolの計算と境界チェックは3.1節でみたとおりです。
// スレッドが計算する出力要素の位置
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
// 境界チェック
if (row < M && col < N) {
・・・(処理内容)
}
また、要素の計算ではfor文が登場します。C++のfor文を初めて見る方もいるかと思いますので、簡単に解説します。for文の宣言部分を再掲します。```
for (int k = 0; k < K; k++) {
(処理内容)
}
pythonのfor分に比べて記載すべき内容が多く面食らうかかしれませんが、これはpythonでは勝手によしなに処理するところを、C++はすべて明示しているに過ぎません。この宣言では以下の内容を指示しています
-
int k = 0にて、ループ変数およびその初期値を定義します- この場合、kは整数で0からループをはじめる)
-
k < Kの箇所で、ループの完了条件を示します- この場合、kがK以上になったら終了
-
k++はループごとにループ変数kをどう変化させるかを示します-
k++はkを1増やすことを示します -
++はインクリメント演算子と呼びます
-
for文内での処理内容は3.2節で見たとおりです。
4.2 CUDA Pythonによる実行コード
4.1のカーネルを含む、pythonによる処理コード一式です。以下の例では、サイズ8,192の正方行列同士の積の計算を実装しています。ちなみにこの計算量は2.4節でみた計算式
を用いると、約1TFLOPsに相当します。
# ①処理の準備
## ライブラリのインポート
from cuda.core.experimental import Device, Program, ProgramOptions, LaunchConfig, launch
import cupy as cp
import numpy as np
import math
import time
## CUDAデバイスの初期化
device = Device()
device.set_current()
stream = device.create_stream()
## CUDA Kernelのソースコード
kernel_source = """
__global__ void matmul(
float *A, float *B, float *C,
int M, int N, int K
) {
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
if (row < M && col < N) {
float c = 0.0f;
for (int k = 0; k < K; k++) {
c += A[row * K + k] * B[k * N + col];
}
C[row * N + col] = c;
}
}
"""
## カーネルのコンパイル
capa = device.compute_capability
program_options = ProgramOptions(
std="c++17",
arch=f"sm_{capa.major}{capa.minor}"
)
program = Program(kernel_source, "C++", options=program_options)
module = program.compile("cubin", name_expressions=("matmul",))
kernel = module.get_kernel("matmul")
# ②データの準備
M, N, K = 8_192, 8_192, 8_192 # 行列のサイズ
A_host = np.random.rand(M, K).astype(np.float32)
B_host = np.random.rand(K, N).astype(np.float32)
print(f"行列サイズ: A({M}×{K}) × B({K}×{N}) = C({M}×{N})")
# GPU計算時間の計測開始
start_gpu = time.time()
# ③GPUメモリへのデータ転送
A_device = cp.asarray(A_host)
B_device = cp.asarray(B_host)
C_device = cp.empty((M, N), dtype=cp.float32)
# ④カーネルの起動設定
block_dim = (16, 16) # 16×16 = 256スレッド/ブロック
grid_dim = (
math.ceil(N / block_dim[0]),
math.ceil(M / block_dim[1])
)
print(f"Block設定: {block_dim}")
print(f"Grid設定: {grid_dim}")
config = LaunchConfig(grid=grid_dim, block=block_dim)
# Kernel計算時間の計測開始
start_kernel = time.time()
# ⑤計算実行
launch(
stream, config, kernel,
A_device.data.ptr,
B_device.data.ptr,
C_device.data.ptr,
cp.uint32(M), cp.uint32(N), cp.uint32(K)
)
device.sync()
# Kernel終了の記録
end_kernel = time.time()
# ⑥結果の取得
C_host_gpu = cp.asnumpy(C_device)
# GPU計算時間の算出
end_gpu = time.time()
time_gpu = end_gpu - start_gpu
# GPU処理時間の取得(データ転送を除く純粋なカーネル実行時間)
time_kernel = end_kernel - start_kernel
# ⑦検証(NumPyでも計算して比較)
start_cpu = time.time()
C_host_cpu = np.matmul(A_host, B_host)
end_cpu = time.time()
time_cpu = end_cpu - start_cpu
# 結果の検証と表示
print(f"\n処理結果:")
print(f"GPU処理時間: {time_gpu:.4f}秒")
print(f"GPU処理時間(カーネルのみ): {time_kernel:.4f}秒")
print(f"CPU処理時間: {time_cpu:.4f}秒")
print(f"高速化率: {time_cpu/time_gpu:.2f}倍")
print(f"結果の一致: {np.allclose(C_host_gpu, C_host_cpu)}")
# FLOPS計算
flops = 2 * M * N * K # 行列積のFLOPS
tflops_gpu = flops / time_kernel / 1e12
print(f"\nGPU性能: {tflops_gpu:.2f} TFLOPS")
4.3 実行結果と考察
上記の実装にもとづく、ランダムなfloatの8,192×8,192行列同士の積の実行時間、およびGPUによる高速化率です。(5回実行の平均)
| 実装 | 実行時間[s] | 高速化率 |
|---|---|---|
| CPU (NumPy) | 1.705 | - |
| GPU | 0.857 | 2.0 |
流石にGPUの十八番である行列積であり、何も最適化を行なっていないナイーブな実装で、かつホスト⇄デバイス間のデータ移送を含めても、CPUの倍の処理速度を出すことができました。
なお、ホスト⇄デバイス間のデータ移送を含めない、Kernel処理のみの処理時間は
| 実装 | 実行時間[s] | FLOPS |
|---|---|---|
| GPU (カーネルのみ) | 0.787 | 1.4 |
本検証を行ったRTX5060Tiは公式では明示されてはいないものの、処理能力は23.7TFLOPSと推定されており、この上限の5%程度しか演算能力を発揮できていません。今後、この上限値に近づけていくための理論・実装を一緒に学んでいきたいと思います。
まとめ
本記事では、行列積のナイーブなGPU実装を解説しました。ナイーブな実装ながら、NumpyによるCPU実行から大幅な高速化を実現することができました。
また、FLOPs、FLOPSによる計算量・速度の評価方法を解説しました。この方法により現状の性能とハードウェアの限界の差を見極めることができ、現実的な最適化目標を設定できるようになります。
次回は、GPUのメモリ構成を解説し、今回ナイーブに実装した行列積をタイリング(Tiling)という手法で高速化してみたいと思います。
Discussion