CUDA PythonではじめるCUDAプログラミング②: 多次元データのマッピング
1. はじめに
筆者はGPUプログラミングを学びながら、並行して記事化を行っています。
前回の記事では、GPUプログラミングの概要を解説し、CUDA Pythonでミニマムの動くCUDAコードを紹介しました。
前回記事では、並列化した計算処理の最小単位をThreadと呼び、Grid-Block-Threadという階層構造を用いてデータに処理を割り当てるということを解説しました。本記事ではここを掘り下げるため、カラー画像のモノクロ化を例にとり、CUDAコードの処理(スレッド)をデータにマッピングしていく方法を解説します。
本記事の流れ
本記事は以下の流れで解説したいと思います。
- 2.データの取り扱い
- モノクロ化の処理内容
- 処理対象のデータの取り扱い
- 3.スレッド(処理)のマッピング
- スレッドを2.のデータにどう割り当てるか(分担するか)を整理します
- また、スレッドが計算対象とするデータをどう参照するのかを整理します
- 4.実装
- 2.と3.解説した内容を、CUDA Pythonを用いて動くコードにします
想定読者
- 本記事でも、Pythonコーディングの経験を前提とします。
- C/C++やCUDAコーディングの知識は前提としません。
- ただし、前回記事の「4.CUDAプログラミングのことはじめ」の内容(ベクトル加算をCUDA Pythonで実装)は前提とします。
2. データの取り扱い
以下で、画像のモノクロ化とはどういう処理なのか、また画像データをどう取り扱うのかを解説します。
2.1 モノクロ化の処理
今回扱うカラー画像のグレー化の処理内容を解説します。カラー画像は単純化してしまうと、2次元の複数の点(ピクセル)に対する赤緑青(RGB)の3色の輝度(0〜255の値)のデータとみなせます。カラー画像のグレー化は、この各ピクセルのRGBの値を、単一の値(輝度)に変換します。
あるピクセルのRGBの輝度の値が(r, g, b)であるとすると、グレー変換後の輝度
上記の式によるカラー→グレーへの変換を可視化すると以下の具合です。左側のカラーの箱の中には(r, g, b)の値を、右側のグレースケールの箱の中にはそれぞれ対応するカラーの箱に対して上式で計算した(L)を表示しています。

(r, g, b)を足し合わせる重み(0.21, 0.72, 0.07)は、足し合わせると1になることに着目してください。これにより、輝度
上記の
2.2 多次元データの平坦化
処理対象のデータはメモリに配置されます。ベクトル加算と同様、まず処理される画像のデータはCPUによりホストメモリに読み込まれ、処理実行時にデバイス(GPU)メモリに配置、処理実施後に処理後のモノクロ画像がホストメモリに移送されます。CUDA Kernelを記載するさい、画像がメモリにどのように保存されるのかを理解する必要がありますので、本節と次節で解説します。
まず、平坦化を説明します。カラー画像は2次元のピクセル毎にRGBの値を持つため、3次元のデータとみなすことができます。一方、メモリは単一のアドレスの値のみで高速にアクセスできるよう、1次元の配列となっています。そのため、3次元のデータを1次元に配置する必要があります。画像の1次元化のイメージを以下に示します。上部に横4×縦3ピクセルの画像を表示しており、各ピクセルのr, g, bの値が1次元に配置される様子を示しています。
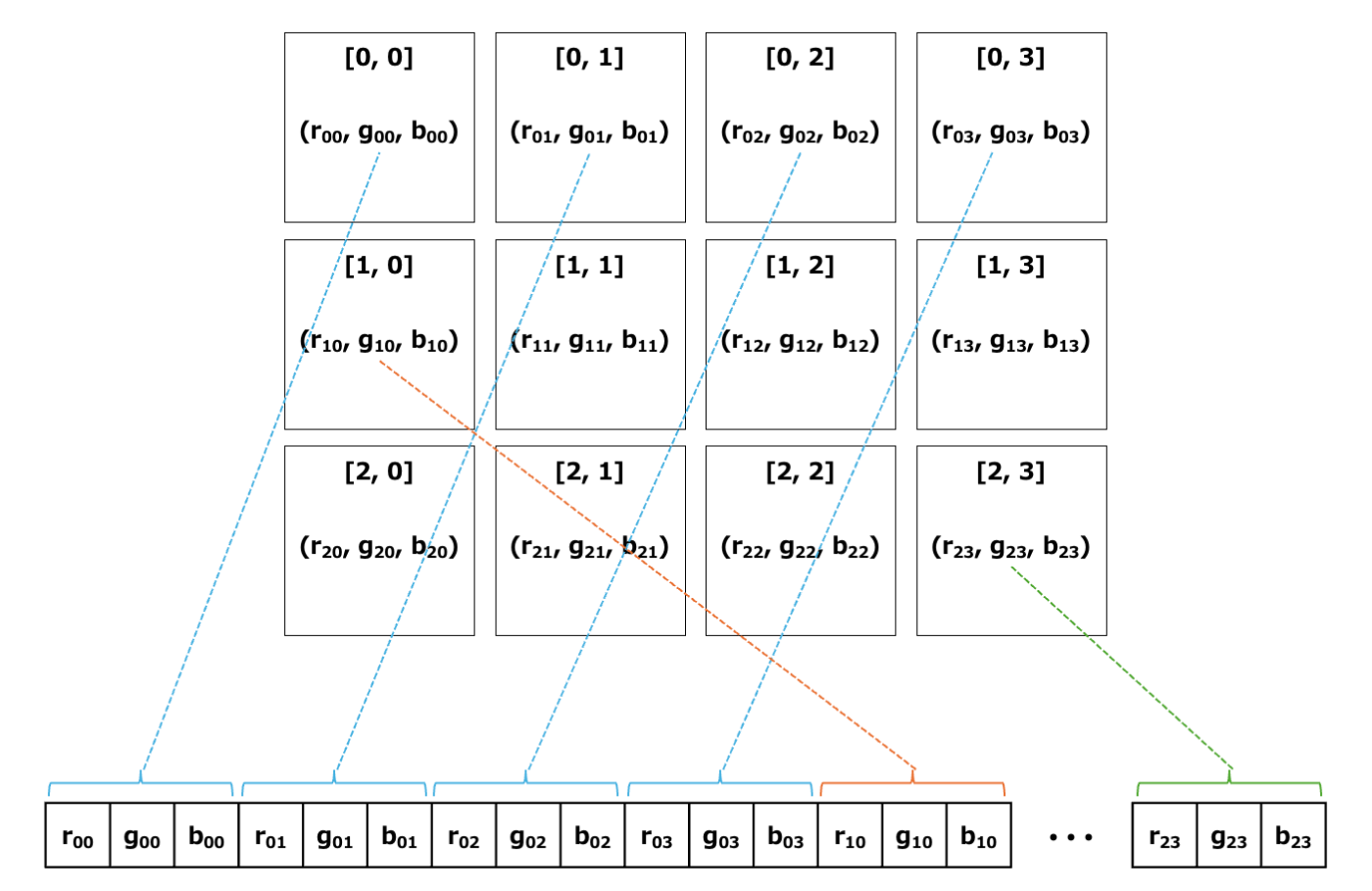
まず、左上のピクセル[0, 0]から横方向に順次r, g, bの値をメモリに並べていきます(水色の線)。そして右端まで来たら次の行の左からr, g, bを並べていきます(オレンジの線)。この形で順次r, g, bを並べていき、右下のピクセルのr, g, bを並べたらメモリへの配置は終了です(緑色の線)。
このような、多次元のデータを1次元配列に変換することを平坦化と呼びます。カラー画像に限らず、すべての多次元データは平坦化して1次元配列としてメモリに配置されることを覚えておいてください。
なお、pythonでの多次元データの平坦化は、numpyのflatten()メソッドにより簡単に行えます。
2.3 カラー画像のメモリへの配置方法
次に、RGBの値(r, g, b)をCUDAでどう表現するのかを見ていきましょう。
まず前提として、0〜255の整数であらわされる(r, g, b)の各値は、C(C++)言語ではunsigned charという型で表現されます。なんじゃこれ、と面食らうと思うと思いますが
unsigned char:0〜255の整数を表示する型
と丸暗記するのが良いです。歴史的な経緯によりややこしい表記となってしまっているので、「符号なしの文字型」というように頑張って解釈するのはやめましょう。
ただ、unsigned charは、二進数でいうと8桁(8ビット)、すなわち1バイトのデータであり、
さらに付け加えると、本当は論理が逆で、「計算処理の都合から(r, g, b)の各色を1バイト、合計3バイトで表現している」というのが正確です。
3. スレッドのデータへのマッピング
ここまででカラー画像のグレー化の処理内容と、画像をメモリに配置する方法を説明しました。次は処理を並列化して各コアに割り当てるため、スレッドをデータに割り当てる(マッピング)方法を確認します。
前回記事でも述べましたが、Kernelを記載するさいは、その計算を行うスレッドの気持ちになることが肝要です。スレッドが計算を行うさい、当然ながらスレッドは自分がどのピクセルを担当するのかを知る必要があります。
以下では横76ピクセル×縦62ピクセルの画像に対して、スレッドをマッピングする例を考えます。各ピクセルの輝度
スレッドのデータへのマッピングのイメージを示します。小さなマスが1ピクセルに相当し、そのマスの輝度

3.1ブロックとグリッド
最初に、ブロックのサイズを決めます。ブロックはスレッドの塊です。上図では16×16の二次元のブロックを想定しています。この場合、1ブロックに対し16×16=256スレッドが割り当てられることになります。ブロックサイズの決め方は3.6節で補足します。
次はグリッド(Grid)の定義です。グリッドはブロックの塊です。グレーのマスで示している画像全体を処理する必要があるので、ブロックはこの画像全体をカバーするように並べられます。この並べられたブロックの集合のことをグリッドと呼びます。
ブロックを画像全体を覆い、かつ不要なブロックを並べないようにする場合、x軸(横)方向およびy軸(縦)方向に必要なブロック数は以下のように計算できます
- x軸: ceil(76/16) = ceil(4.75) = 5
- y軸: ceil(62/16) = ceil(3.875) = 4
なお、ceil(x)はx以上の最小の整数です(ようは小数点以下を切り上げる関数)。xが整数の場合はceil(x)の値はxそのままです。この5×4の系20ブロックの集合が、76×62ピクセルの画像のモノクロ化処理のグリッドとなります。
なお、ブロックのサイズは3.6節でみるように、効率性等の観点で決められ、インプットデータのサイズは考慮されないことが多いです。このため、画像の通り画像のグレーのマスの範囲からはみ出るスレッド(白色のマス)が発生します。このはみ出た部分の扱いについては3.4節で解説します。
3.2 ブロックおよびスレッドのインデックス
ブロックおよびスレッドにはそれぞれblockIdxおよびthreadIdxという構造体によりインデックスが与えられます。インデックスは0はじまりであることに留意してください。
まず、上記のグリッドは5×4ブロックより構成されます。そのため、ブロックのインデックスは以下の整数値をとります
- x軸方向のインデックス(
blockIdx.x): 0〜4 - y軸方向のインデックス(
blockIdx.y): 0〜3
上記の図では(blockIdx.x, blockIdx.y) = (2, 1)のブロックを青色で強調表示しています。
次に、グリッドのうち一つのブロックは16×16スレッドにより構成されます。そのため、スレッドのインデックスは以下の値をとります
- x軸方向のインデックス(
threadIdx.x): 0〜15 - y軸方向のインデックス(
threadIdx.y): 0〜15
上記の図では(threadIdx.x, threadIdx.y) = (2, 3)のスレッドをオレンジ色で強調表示しています。
なお、補足しますと、特定のブロックに所属するスレッドは全て同じblockIdxの値を持ちます。画像の例では、青色のスレッドたちは(blockIdx.x, blockIdx.y) = (2, 1)のブロックに所属するため、青色のどのスレッドでblockIdx.xの値を取得しても全て2を返し、blockIdx.yは1を返します。
3.3 各スレッドが処理するピクセルの特定
まず、オレンジ色で着色したスレッドについて考えましょう。自身が処理すべきピクセルの列(col、横方向の座標)および行(row、縦方向の座標)を計算します。列については、まずこの青色のブロックより左に2ブロック(横に16ピクセル)あり、また青色のブロックの中ではオレンジ色のスレッドより左にthreadIdx.x=2スレッドあります。そのため計算対象の横方向の座標であるcolは
col = 2*16 + 2 = 34
となります。同様に縦方向のインデックスrowは、
row = 1*16 + 3
となります。
ここで、座標が0はじまりであることに留意しながら、「自身が所属するブロックより左に何ブロックがあるかの数値が、自身のblockIdx.xの値と等しい」ことを、納得するまで図と睨めっこしてください。また「自分が所属するブロック内で、自分より左に何スレッドあるかの数値が自身のthreadIdx.xの値と等しい」ことも確認してください。上記の考え方に基づき一般化すると、スレッドが計算すべきピクセルの座標は
col = blockIdx.x*blockDim.x + threadIdx.x
row = blockIdx.y*blockDim.y + threadIdx.y
となります。
3.4 境界チェック
3.1節で触れましたが、下の画像のとおり、ブロックを画像に対して敷き詰めると、端のブロックで画像からはみ出るセル(スレッド)が現れてしまいます。具体的には、今回扱う画像は横76×縦62ピクセルの画像ですが、以下の画像でオレンジ色に着色したセルはcol ≧ 76でx軸方向にはみ出ており、紫色に着色したセルはrow ≧ 62でy軸方向にはみ出て、赤色のセルは両方に該当します。(くどいですが、インデックスは0はじまりであることに留意してください)
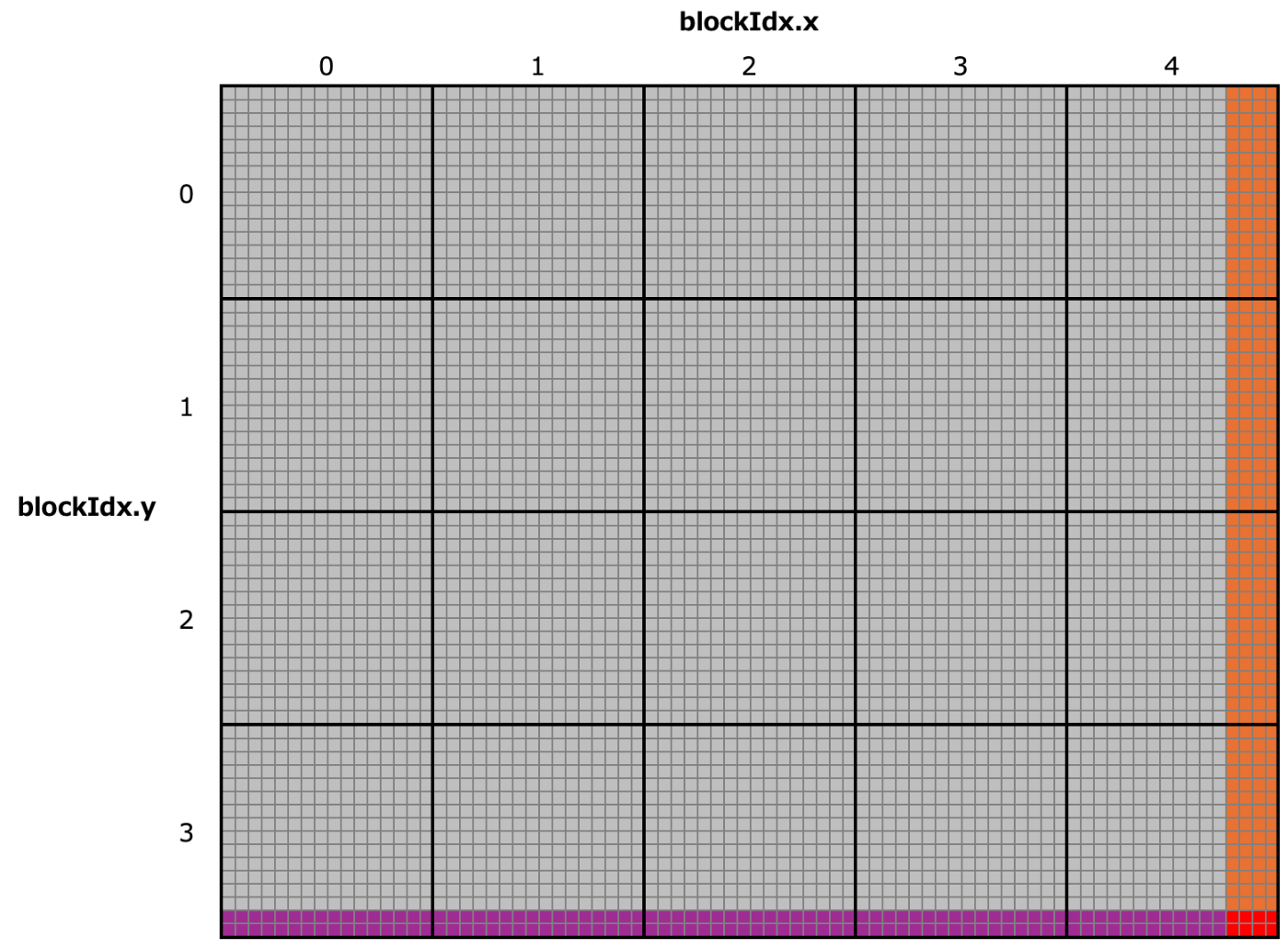
このような、本来アクセスすべきでない箇所のインデックスに対して、メモリの読み書きを行うのは非常に危険です。そのため、このような領域を割り振られたスレッドでは、処理を実行しないようにする措置(境界チェック)を取る必要があります。
境界チェックは、Kernelのなかで入力画像の横のピクセル数をwidth、縦のピクセル数をheightとして、if文を用いて以下のように記載します。
// 境界チェック
if (col < width && row < height) {
〜〜カーネルの処理内容〜〜
}
3.5 スレッド別のメモリアクセス
3.3節で各スレッドが計算すべきcolおよびrowを特定し、また3.4節で境界チェックを挟んだので、安全にメモリにアクセスできるようになりました。次に、スレッドがメモリから計算対象のピクセルのRGB値を取得する方法を考えます。
2.2節と2.3節で見たように、画像データは1次元配列として平坦化されてメモリに配置されています。横幅widthピクセル、高さheightピクセルの画像において、座標(col, row)のピクセルは、画像を平坦化し左上のピクセルを0番として番号をつけていくとrow * width + col番目のピクセルになります(これをpixcel_indexとしましょう)。そして、各ピクセルは3つの値を持つので、座標(col, row)のピクセルのRGBのうち最初のrの値は、メモリの配列の3*(row * width + col)番目の要素に格納されることになります(これをbase_indexとしましょう)。そしてgはbase_indexの隣(+1)、bはbase_indexの隣の隣(+2)の値となります。
上記をコード風に表現すると以下のようになります。
pixcel_index = row * width + col
base_index = 3 * pixcel_index
r = input[base_index]
g = input[base_index + 1]
b = input[base_index + 2]
この計算により、2次元の座標から1次元配列内の適切な位置を特定できます。
上記の計算の具体例を、2.2節の横4×縦3ピクセルの事例について示しましたので、こちらを眺めて上記のインデックスの計算を具体的にイメージできるまで眺めてください。

3.6 ブロックサイズ選択の留意点
上記の例では天下り的にブロックサイズを16×16=256としましたが、こちらは本来色々な要素を考慮して決定する必要があります。
ここでは、3.1節で天下り的に決めたブロックサイズについて、決定にあたって考慮すべき事項を並べます。
ハードウェアによる制限
ブロックあたりのスレッド数は、現代的なアーキテクチャでは1,024個に制限されています。今回設定したブロックサイズは16×16=256のため、この制限を満たしています。
ワープの考慮
別記事で解説しますが、スレッドはワープ(Warp, 日本語でいうと束)という単位で処理されます。そして、今存在するGPUは1ワープ=32スレッドです。スレッドがこのワープという単位に分割される都合上、ブロックのサイズ(ブロックあたりのスレッド数)はワープの倍数、すなわち32の倍数に設定する必要があります。なお、32の倍数に設定しない場合、ブロック内の最後のワープがスレッドを余らせてしまい、計算できないコアが生じてしまうので、パフォーマンス低下につながります。
今回設定したブロックサイズ16×16=256は、32のちょうど8倍であるため、この制限も満たしています。
ちなみに、1ワープ=32スレッドというのはこれまでのアーキでの話であり、未来永劫変化しないわけではないことに留意してください。将来たとえば1ワープ=64スレッドというアーキが出現した場合、その変更に応じブロックサイズを見直す必要があります。
パフォーマンスの考慮
これが一番大切で、ブロックサイズの選択はパフォーマンスに直結します。解説のためにはいくつか前提知識が必要となるため、今後複数記事で解説していきます。ブロックのサイズは大きすぎても小さすぎてもパフォーマンスに悪影響を与えます。
4.実装
2章で画像データの扱いを整理し、3章でスレッドをデータにマッピングする方法を見ました。以下は、ここまでの内容を統合して実装を行なっていきます。
4.1 CUDA Kernelの実装
ここまで説明したことをまとめると、CUDA Kernelの実装は以下のようになります。
__global__ void rgb_to_grayscale(
unsigned char *input, // 入力画像(RGB)
unsigned char *output, // 出力画像(グレースケール)
int width, // 画像の幅
int height // 画像の高さ
) {
// スレッドが処理するピクセルの座標を計算
int col = blockIdx.x * blockDim.x + threadIdx.x;
int row = blockIdx.y * blockDim.y + threadIdx.y;
// 境界チェック
if (col < width && row < height) {
// 平坦化したピクセル位置を計算
int pixel_index = row * width + col;
// RGB値の取得(3チャンネル分の連続するメモリのアドレスから読み取り)
int base_index = pixel_index * 3;
unsigned char r = input[base_index];
unsigned char g = input[base_index + 1];
unsigned char b = input[base_index + 2];
// グレースケールに変換し、出力画像に格納
output[pixel_index] = 0.21*r + 0.72*g + 0.07*b;
}
}
上記のカーネルのうち、入力画像のinputはピクセル数×3(RGBの各値)の長さの配列であることに対し、出力画像outputはピクセル数の長さの配列であることに注意してください。そのため、pixcel_index番目のピクセルについて、inputは3*pixcel_indexがベースアドレスであるのに対し、outputはpixcel_indexのアドレスに保存されます。
4.2 CUDA Pythonによる実行コード
次に、上記のKernelをCUDA Pythonから呼び出す実装例全体を示します。①〜⑦は前記事の4.2節に対応していますので、適宜参照してください。
# ①処理の準備
## ライブラリのインポート
from cuda.core.experimental import Device, Program, ProgramOptions, LaunchConfig, launch
import cupy as cp
import numpy as np
from PIL import Image
import math
import time
## CUDAデバイスの初期化
device = Device()
device.set_current()
stream = device.create_stream()
## CUDA Kernelのソースコード
kernel_source = """
__global__ void rgb_to_grayscale(
unsigned char *input,
unsigned char *output,
int width,
int height
) {
int col = blockIdx.x * blockDim.x + threadIdx.x;
int row = blockIdx.y * blockDim.y + threadIdx.y;
if (col < width && row < height) {
int pixel_index = row * width + col;
int base_index = pixel_index * 3;
unsigned char r = input[base_index];
unsigned char g = input[base_index + 1];
unsigned char b = input[base_index + 2];
output[pixel_index] = 0.21*r + 0.72*g + 0.07*b;
}
}
"""
## カーネルのコンパイル
capa = device.compute_capability
program_options = ProgramOptions(
std="c++17",
arch=f"sm_{capa.major}{capa.minor}"
)
program = Program(kernel_source, "C++", options=program_options)
module = program.compile("cubin", name_expressions=("rgb_to_grayscale",))
kernel = module.get_kernel("rgb_to_grayscale")
# ②データの準備
## サンプル画像の生成または読み込み
# 例:1億画素(12,032 × 9,024)のランダムなカラー画像を生成
width = 12_032
height = 9_024
rgb_image_host = np.random.randint(
0, 256,
(height, width, 3),
dtype=np.uint8
)
# 実際の画像ファイルを読み込む場合
# image = Image.open("GPU.jpg")
# rgb_image_host = np.array(image)
# height, width = rgb_image_host.shape[:2]
# RGB画像を1次元配列に平坦化
rgb_flat_host = rgb_image_host.flatten()
print(f"画像サイズ: {width}×{height}")
# GPU計算時間の計測開始
start_gpu = time.time()
# ③GPUメモリへのデータ転送
rgb_flat_device = cp.asarray(rgb_flat_host)
gray_device = cp.empty(width * height, dtype=cp.uint8)
# ④カーネルの起動設定
## 2次元のBlock構成(16×16 = 256スレッド/ブロック)
block_dim = (16, 16)
grid_dim = (
math.ceil(width / block_dim[0]),
math.ceil(height / block_dim[1])
)
print(f"Block設定: {block_dim}")
print(f"Grid設定: {grid_dim}")
config = LaunchConfig(grid=grid_dim, block=block_dim)
# ⑤計算実行
launch(
stream, config, kernel,
rgb_flat_device.data.ptr,
gray_device.data.ptr,
cp.uint32(width),
cp.uint32(height)
)
device.sync()
# ⑥結果の取得
gray_host = cp.asnumpy(gray_device)
# GPU計算時間の算出
end_gpu = time.time()
time_gpu = end_gpu - start_gpu
# ⑦検証(CPUでも計算を実行し、結果を比較)
## CPUでのグレースケール変換
start_cpu = time.time()
gray_cpu = (
0.21 * rgb_image_host[:, :, 0] +
0.72 * rgb_image_host[:, :, 1] +
0.07 * rgb_image_host[:, :, 2]
).astype(np.uint8).flatten()
end_cpu = time.time()
time_cpu = end_cpu - start_cpu
print(f"\n処理結果:")
print(f"GPU処理時間: {time_gpu:.4f}秒")
print(f"CPU処理時間: {time_cpu:.4f}秒")
print(f"高速化率: {time_cpu/time_gpu:.2f}倍")
# 結果画像の保存(オプション)
gray_image = gray_host.reshape((height, width))
Image.fromarray(gray_image, mode='L').save("output_gray.png")
print("グレースケール画像を 'output_gray.png' として保存しました")
4.3 実行結果と考察
1億画素(12,032 × 9,024ピクセル)のランダムなカラー画像で実行した場合の実行時間の比較です。(5回実行の平均時間)
| GPU[s] | CPU[s] | 高速化率 |
|---|---|---|
| 0.067 | 0.547 | 8.2 |
今回は苦労した甲斐もあり、8倍以上の高速化を達成できました!
やはりグラフィックス処理に特化したプロセッサなので、データ型および演算処理との相性が非常によく、ナイーブな実装でも大幅に高速化されますね。
ちなみに、ちゃんとグレースケールになっているかを目視で確認したいので、以下のイラストやのGPU画像を上記コードで変換してみました。

変換後の画像は以下のとおりで、自然な処理結果になっていそうです。

まとめ
本記事では、カラー画像のモノクロ化を例に、2次元データへのスレッドマッピングとCUDA実装を解説しました。Grid-Block-Threadの階層構造を活用して2次元データを処理する方法と、平坦化された1次元配列からデータを取得する方法を学びました。また、ナイーブな実装ながら、実用的な処理をGPUにより大幅に高速化する実例を見ることができました。
次回は、より複雑な演算である行列積のGPU処理を解説します。行列積は今後の最適化の検討のベースケースとしますし、ディープラーニングへの適用の入り口になる内容ですので、ぜひ次回記事もご覧ください。
Discussion