はじめに
背景
その1、その2ときた、第32回日本数学オリンピック予選(2022年1月10日実施分)の解説、今回で完結となります。まだご覧になってない場合は、その1から読まれることをお勧めします。
参考情報
解説
それでは、今回の「その3」では、第11問、第12問の最後2問を解説していきます。
第11問
- 問題: 正の整数nに対して、f(n) を
f(n)=\begin{dcases} n^{100} & (nの各桁の和が偶数のとき), \\ -n^{100} & (nの各桁の和が奇数のとき) \end{dcases}
と定める。S=f(1)+f(2)+\cdots+f(10^{100}-1)とするとき、Sが5^mで割り切れるような最大の非負整数mを求めよ。ただし、Sは0ではない。
- 答: 5074
最後の方になるとなかなか一筋縄では解けない問題になってきます。特に100乗や、10^{100}-1という膨大な数など、実際に計算を試せない部分をどう扱えるようにしていくか、工夫が必要になります。
まず目につくのは、総和を求める f(n) の引数が 1\sim 99\cdots 99 と100桁の範囲となっている部分ですが、このままではどうしようもありません。ここの桁数をどう落としていくかを考えます。
ここで、0 も追加してみると、0\sim 99\cdots 99(=10^{100}-1) というのは、10^{99}の位の0\sim 9と、その下位の桁の0\sim 99\cdots 99(=10^{99}-1)の組み合わせであり、1桁ずつ0\sim 9の計算に引き落としていけるのではないかと考えます。
そのために、次のような関数 s(n)を定義します。
- s(n)=\begin{dcases} 1 & (nの各桁の和が偶数のとき), \\ -1 & (nの各桁の和が奇数のとき) \end{dcases}
こうすることで、
\begin{align*}
S&=s(0)\cdot 0^{100}+s(1)\cdot 1^{100}+\cdots+s(10^{100}-1)(10^{100}-1)^{100} \\
&=\sum_{k=0}^{10^{100}-1} s(k)k^{100}
\end{align*}
と、S の式を書き換えることができます。
この式をよく見ると、10^{100}-1 の指数部分の100と、k^{100}の指数部分の100、同じ100ですが意味合いの違う2種類の数がでてきます。
そこで、次のように総和を計算する G(m,n) を定義します。
- G(m,n)=\sum_{k=0}^{10^{n}-1} s(k)k^m~~(0\le m,~1\le n)
こうすることで、S=G(100,100) と更に書き換えることができます。
このようにGを定義して、桁を落としていこうとするわけですが、先にsの性質として、s(1234)=s(1)s(234) のように、桁を分離した時に積の関係が現れることを意識しておきます。
特に s(0)=1 なので s(n)=s(0)s(n) ということで、上位に0の桁を付け足したとしても不都合がない定義になっています。
そして、いよいよ桁を落としていきます。1\lt nに対し、最上位桁・下位の桁での2重和の形にし、更にm乗の部分を2項定理で整理していきます。
※パラメータによっては0^0の計算が出てきますが、それは0^0=1としておきます。
\begin{align*}
G(m,n)&=\sum_{k=0}^{10^{n}-1} s(k)k^m \\
~&=\sum_{i=0}^9 \sum_{j=0}^{10^{n-1}-1} s(i\cdot 10^{n-1}+j)(i\cdot 10^{n-1}+j)^m \\
~&=\sum_{i=0}^9 \sum_{j=0}^{10^{n-1}-1} s(i\cdot 10^{n-1}+j)\sum_{k=0}^m ~_mC_k(i\cdot 10^{n-1})^k\cdot j^{m-k} \\
\end{align*}
ここに、上で確認した「桁を分離した時のs(n)の積の関係」を適用して、更に3重和の形を整理します。
\begin{align*}
G(m,n)&=\sum_{i=0}^9 \sum_{j=0}^{10^{n-1}-1} s(i\cdot 10^{n-1}+j)\sum_{k=0}^m ~_mC_k(i\cdot 10^{n-1})^k\cdot j^{m-k} \\
&=\sum_{i=0}^9 \sum_{j=0}^{10^{n-1}-1} \sum_{k=0}^m s(i)s(j)~_mC_k(i\cdot 10^{n-1})^k\cdot j^{m-k} \\
&=\sum_{k=0}^m 10^{k(n-1)}~_mC_k \sum_{i=0}^9 \sum_{j=0}^{10^{n-1}-1} s(i)s(j)i^k\cdot j^{m-k} \\
&=\sum_{k=0}^m 10^{k(n-1)}~_mC_k \bigg( \sum_{i=0}^9 s(i)i^k \bigg)\bigg( \sum_{j=0}^{10^{n-1}-1} s(j)j^{m-k} \bigg) \\
\end{align*}
このように、パラメータの依存関係のない多重和なので、総和の積に書き換えることができます。そうして、書き換えた部分は G の形に他ならないため、結局、次のように整理できます。
\begin{align*}
G(m,n)&=\sum_{k=0}^m 10^{k(n-1)}~_mC_k \bigg( \sum_{i=0}^9 s(i)i^k \bigg)\bigg( \sum_{j=0}^{10^{n-1}-1} s(j)j^{m-k} \bigg) \\
~&=\sum_{k=0}^m 10^{k(n-1)}~_mC_k G(k,1)G(m-k,n-1) \\
\end{align*}
これにより、桁を落とす漸化式を導くことができました。これを適用すれば S であれば次のように書き換えられます。
\begin{align*}
S&=G(100,100) \\
~&=~_{100}C_0 G(0,1)G(100,99) \\
~&~~+10^{99}~_{100}C_1 G(1,1)G(99,99) \\
~&~~+10^{2\cdot 99}~_{100}C_2 G(2,1)G(98,99) \\
~&~~+\cdots \\
~&~~+10^{99\cdot 99}~_{100}C_{99} G(99,1)G(1,99) \\
~&~~+10^{100\cdot 99}~_{100}C_{100} G(100,1)G(0,99)
\end{align*}
…桁を落とせたのは良いですが、2項定理のおかげで項数が増えてしまって、お世辞にも簡単になったようには見えません。
ここで、一旦整理するのは脇に置いておいて、具体的な G の値を考えてみます。
例えば、単純な例として次のように G(1,1)=-5 と計算できます。
\begin{align*}
G(1,1)&=s(0)\cdot 0+s(1)\cdot 1+s(2)\cdot 2+s(3)\cdot 3+s(4)\cdot 4+s(5)\cdot 5+s(6)\cdot 6+s(7)\cdot 7+s(8)\cdot 8+s(9)\cdot 9 \\
~&=0-1+2-3+4-5+6-7+8-9 \\
~&=-5
\end{align*}
また、各桁の和が偶数/奇数になるのが半々になることに気付けば、G(0,n)=0 であることが分かります。であれば、先ほどのS=G(100,100)の計算で出てくる101項分の内、最初と最後の項はG(0,1),G(0,99)が含まれるので消えてくれることになります。すなわち、
\begin{align*}
S&=G(100,100) \\
~&=~_{100}C_0 G(0,1)G(100,99) \\
~&~~+10^{99}~_{100}C_1 G(1,1)G(99,99) \\
~&~~+10^{2\cdot 99}~_{100}C_2 G(2,1)G(98,99) \\
~&~~+\cdots \\
~&~~+10^{99\cdot 99}~_{100}C_{99} G(99,1)G(1,99) \\
~&~~+10^{100\cdot 99}~_{100}C_{100} G(100,1)G(0,99) \\
~&=10^{99}~_{100}C_1 G(1,1)G(99,99) \\
~&~~+10^{2\cdot 99}~_{100}C_2 G(2,1)G(98,99) \\
~&~~+\cdots \\
~&~~+10^{99\cdot 99}~_{100}C_{99} G(99,1)G(1,99) \\
\end{align*}
この「Gの値が0になるので項が減る」という部分にピンと来るかどうか。これが最後の分かれ道になります。してみると、問題文にわざわざ「Sは0ではない」と書いてあるのはパラメータの組み合わせによっては0となることがあるということで、実は大きなヒントになっていたのです。
この点、結論から先に言うと m\lt n\Rightarrow G(m,n)=0 です。つまり G(0,n)=0 はこのmの最小での場合に相当していたわけです。
先ほど計算した中で G(1,1)=-5 は0にならないギリギリのラインだったということになりますが、本当に0になるかの確認としてG(1,2)を試してみます。
\begin{align*}
G(1,2)&=\sum_{k=0}^1 10^{k(2-1)}~_1C_k G(k,1)G(1-k,2-1) \\
~&=~_1C_0 G(0,1)G(1,1) + 10^1~_1C1 G(1,1)G(0,1) \\
~&=~_1C_0 \cdot 0\cdot G(1,1) + 10^1~_1C1 G(1,1)\cdot 0 \\
~&=0
\end{align*}
確かに0となりました。念のため、帰納法で示しておきます。
既に G(0,n)=0 は分かっていますので、\forall n\gt m, G(m,n)=0\Rightarrow \forall n\gt m+1, G(m+1,n)=0 の部分が示せれば十分です。
n\gt m+1 の時、m+1-1\lt n-1 であることから、1\ge k\Rightarrow m+1-k\gt n-1\Rightarrow G(m+1-k,n)=0
よって、
\begin{align*}
G(m+1,n)&=\sum_{k=0}^{m+1} 10^{k(n-1)}~_mC_k G(k,1)G(m+1-k,n-1) \\
~&=~_mC_0 G(0,1)G(m+1,n-1)+\sum_{k=1}^{m+1} 10^{k(n-1)}~_mC_k G(k,1)G(m+1-k,n-1) \\
~&=~_mC_0 \cdot 0\cdot G(m+1,n-1)+\sum_{k=1}^{m+1} 10^{k(n-1)}~_mC_k G(k,1)\cdot 0 \\
~&=0
\end{align*}
と、上のように示せます。\sum の各項が 0 になるのがミソです。
では、このことを利用して 2\le n に対し、 G(n,n) を再度整理していきます。
\begin{align*}
G(n,n)&=\sum_{k=0}^{n} 10^{k(n-1)}~_nC_k G(k,1)G(n-k,n-1) \\
~&=~_nC_0 G(0,1)G(n,n-1)+10^{n-1}~_nC_1 G(1,1)G(n-1,n-1)+\sum_{k=2}^{n} 10^{k(n-1)}~_nC_k G(k,1)G(n-k,n-1) \\
~&=~_nC_0 \cdot 0\cdot G(n,n-1)-5n\cdot 10^{n-1}G(n-1,n-1)+\sum_{k=2}^{n} 10^{k(n-1)}~_nC_k G(k,1)\cdot 0 \\
~&=-5n\cdot 10^{n-1}G(n-1,n-1)
\end{align*}
ほとんど全て0で消えてくれますので、1項分だけが残ります。
これでやっと、分かり易い漸化式 G(n,n)=-5n\cdot 10^{n-1}G(n-1,n-1) が出ました。
この漸化式を繰り返し適用して S=G(100,100)を計算すると、次のようになります。
\begin{align*}
S&=G(100,100) \\
~&=(-5)^{99}\cdot (100\cdot 99\cdot\cdots\cdot 2)\cdot 10^{99+98+\cdots+1}G(1,1) \\
~&=(-5)^{99}\cdot (100\cdot 99\cdot\cdots\cdot 2)\cdot 10^{99+98+\cdots+1}\cdot(-5) \\
~&=(-5)^{100}\cdot 100!\cdot 10^{4950}
\end{align*}
最終的に問われているのは「Sが5^mで割り切れるような最大の非負整数m」で、つまり言い方を変えると「Sを何回5で割りきることができるか」でした。
式の中で (-5)^{100} の部分では100回、100! の部分では24回 ( \lfloor \frac{100} 5\rfloor +\lfloor \frac{100} {5^2}\rfloor=24 から )、10^{4950}の部分では4950回、5で割り切ることができます。
なので、Sを何回5で割り切れるかというと、それは 100+24+4950=5074回で、この 5074 が答えになります。
第12問
- 問題: AB=11, AC=10 をみたす鋭角三角形ABCがあり、その垂心をH、辺BCの中点をMとする。三角形ABCの内部の点Pが三角形BHCの外接円上にあり、\angle ABP=\angle CPM, PM=3をみたしている。このとき、線分BCの長さを求めよ。
- 答: 2\sqrt{21}
最後の問題は幾何で来ました。問題文だけ見てもさっぱり掴みどころがありません。これをいかに「計算できる」形に情報を整理して変形していけるか、それが問われることになります。
まず、何はともあれ図を描いてみます。
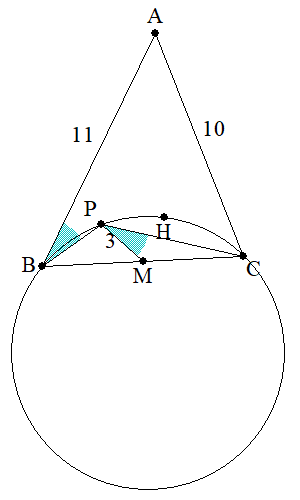
しかし、描いただけでは糸口が見つかりません。
その理由は2つあり、
- 垂心とそれを含む三角形の外接円と言われてもどう条件を活用していいか分からない
-
\angle ABP=\angle CPM と言われても、この2角がどう絡むのか分からない
というところが主なところかと思います。
なので、まずは「垂心」に切り込んでいきます。
そこで、\triangle ABCと垂心H、それから外接円に絞った図で考えてみます。
ここに、Bを通るBHに垂直な直線、Cを通るCHに垂直な直線を引くと、実はその交点Dも\triangle BHCの外接円の周上にくることが分かります。加えて、\square ABDCは平行四辺形となります。
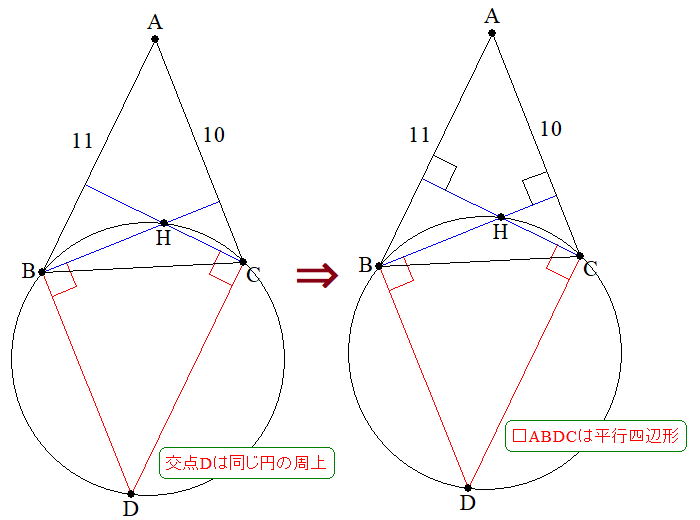
これは、第4問でもあった「向かいあう角が共に直角な四角形に外接する円がある(この場合、既存の外接円に一致する)」ことと、垂心の性質と併せてAB\perp CH,~DC\perp CH\Rightarrow AB/\!/DC,~~AC\perp BH,~BD\perp BH\Rightarrow AC/\!/BD と2つの平行の関係が出てくるからです。
「そんな垂直な直線引くなんて思いつくか!!」と思われるかも知れませんが、次の図のように垂心Hを持つ\triangle ABCと、大きさを倍にした\triangle A'B'C'に関して、AH,BH,CHは\triangle A'B'C'の各辺の垂直二等分線になることで、Hが\triangle A'B'C'の外心であること、\triangle A'BC,~\triangle AB'C,~\triangle ABC'の各外接円の周上に来ることを知っていれば、何となく思いつくのではないかと思います。
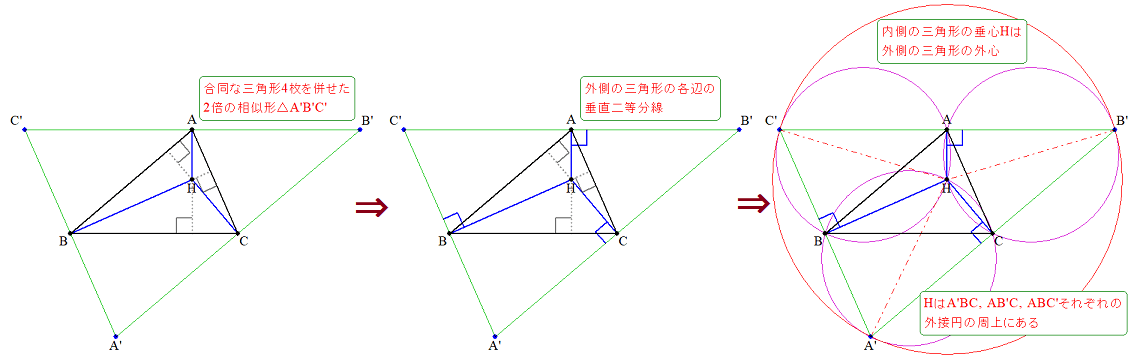
しかし、依然として \angle ABP=\angle CPM の条件が使い辛いことには変わりありません。
そこで、直線BP,DCの交点をRとして導入します。\square ABDCが平行四辺形ですから、\angle ABP=\angle BRC として同じ大きさの角が移ってきます。
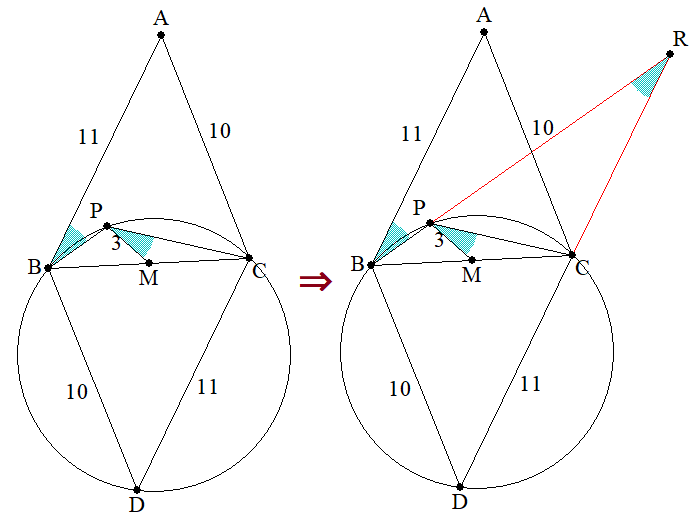
この時点で実はAの存在は忘れて構いません。
最後に、\angle CPMを活用するための一手として、MPに平行な直線CQを引きます。
※錯角の関係により\angle CPM=\angle PCQ となります。
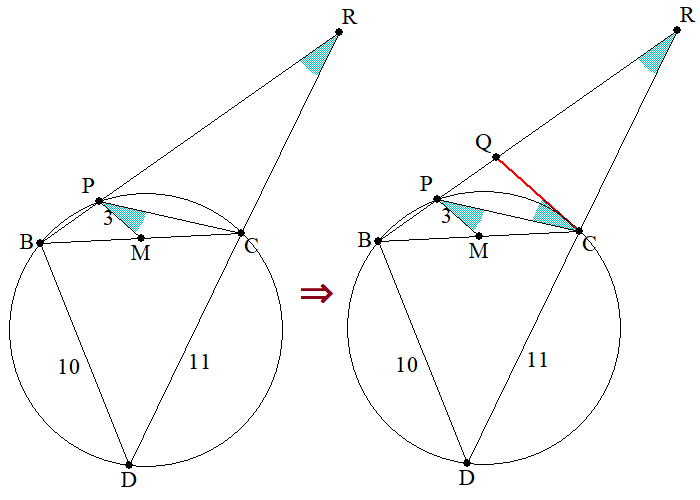
このCQは、2組の相似関係を睨んだ、一石二鳥の手となります。すなわち、以下の2条件です。
-
\angle P共通、\angle PCQ=\angle PRC による、\triangle PCQ\text{∽}\triangle PRC
-
\angle MPC=\angle QCP\Rightarrow MP/\!/CQ\Rightarrow\triangle BMP\text{∽}\triangle BCQ
※この相似と、MがBCの中点であることから、BP=PQ,~QC=2PM=6
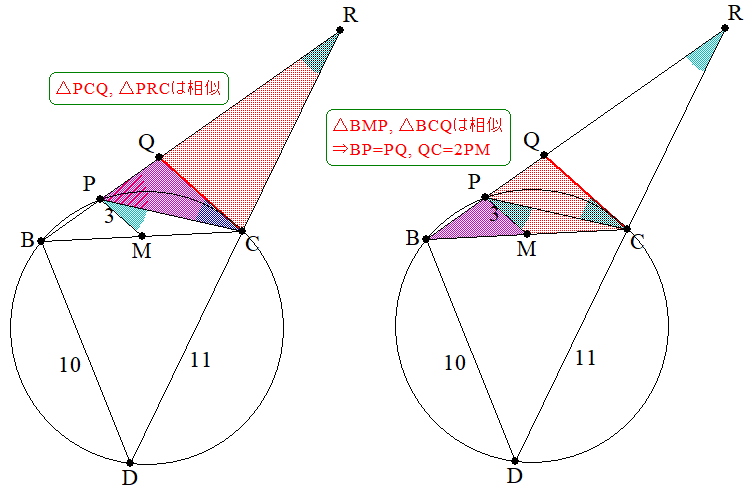
これでMの存在も忘れることができます。
最後に残った外接円の条件を、\angle RPC=\angle D に変換して、円のことも忘れてしまいます。
これで、糸口の見えなかった図形が、色々と等しい角・辺があり、相似形の利用で何とかなりそうな三角形の問題に帰着されました。
後は、求めるBCの長さをx、相似形の核となる部分としてPQ=a,~PC=bと置いておきます。
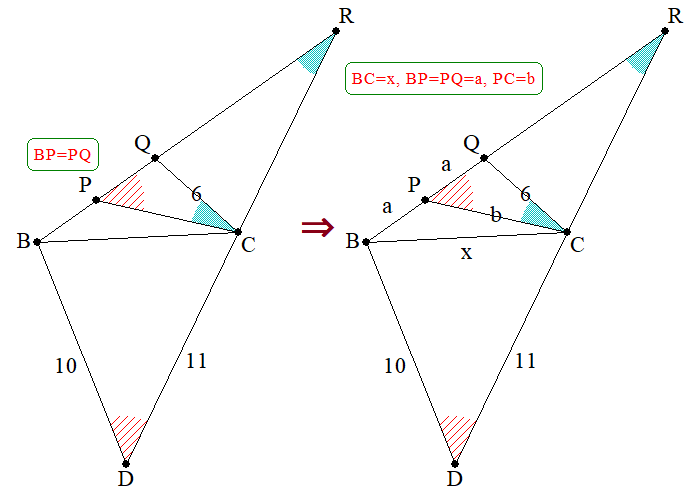
では、いよいよ長さの関係を見ていきます。
1つめは、\triangle CQBに関する中線定理 BC^2+QC^2=2(PQ^2+PC^2)です。
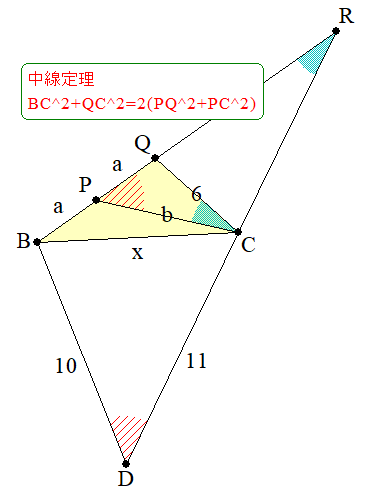
ここから、次が分かります。ついでに、a,bの具体的な値を求める必要がなく、a^2+b^2が分かれば十分ということも分かります。
- x^2+6^2=2(a^2+b^2)\Rightarrow x=\sqrt{2(a^2+b^2)-36}
2つめは、2つの角が共通であることによる相似です。
-
\angle P共通、\angle PCQ=\angle PRC による、\triangle PCQ\text{∽}\triangle PRC\Rightarrow PR:PC=PC:PQ
-
\angle QPC=\angle BDR,~\angle QCP=\angle BRD による、\triangle QPC\text{∽}\triangle BDR\Rightarrow BD:BR=QP:QC
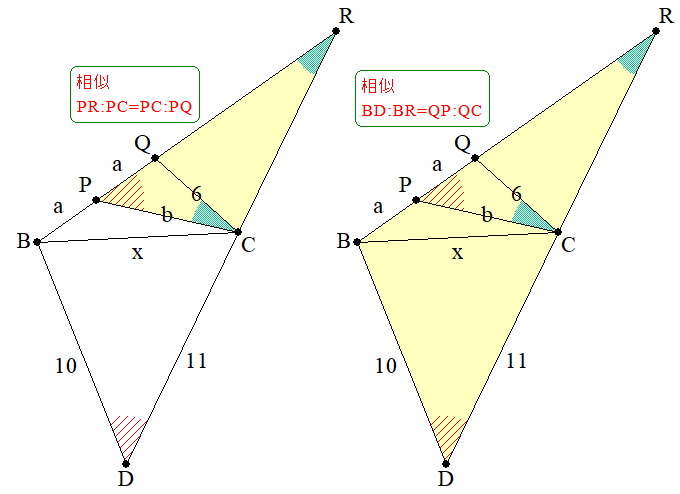
これを整理して、
-
PR:PC=PC:RQ\Rightarrow PR=\frac{PC^2}{RQ}=\frac{b^2} a
\Rightarrow BR=BP+PR=a+\frac{b^2} a=\frac{a^2+b^2} a
- BD:BR=QP:QC\Rightarrow BR=\frac{BD\cdot QC}{QP}=\frac{10\cdot 6} a=\frac{60} a
この2条件から、BRを表す2通りの式 BR=\frac{a^2+b^2} a,~BR=\frac{60} a を比較して、a^2+b^2=60 が分かります。
最終的に、x=\sqrt{2(a^2+b^2)-36}=\sqrt{2\cdot 60-36}=2\sqrt{21} を計算し、これが答えとなります。
おわりに
流石に最後の2問、まずどう手を付けて良いか戸惑う上、答えに辿り着くまでなかなか長い道のりを要する手強い問題でした。しかし、決して手が届かないわけでもないことも言えると思います。
これで予選の問題、全部の解説を挙げました。手が届きそうだと感じて、かつ年齢的に資格がある人は、是非来年挑戦してみてはいかがでしょうか。









Discussion