🏅

日本数学オリンピック(JMO)2022年予選解答私的解説その2

2022/01/22に公開

math

jmo

数学オリンピック

tech

はじめに

背景

その1に引き続き、第32回日本数学オリンピック予選(2022年1月10日実施分)の解説です。その1をまだご覧になってない場合は、そちらから読まれることをお勧めします。

参考情報

その1 … 日本数学オリンピック(JMO)2022年予選解答私的解説その1
その3 … 日本数学オリンピック(JMO)2022年予選解答私的解説その3(完)
問題公開先 … https://www.imojp.org/archive/mo2022/jmo2022/problems/jmo32yq.html

解説

それでは、今回の「その2」では、第7問～第10問の後半4問を解説していきます。

第7問

問題: $\angle BAC=90\degree, AB=AC=7$ である直角二等辺三角形 $ABC$ がある。辺 $BC, CA, AB$ 上にそれぞれ点 $D,E,F$ があり、 $\angle EDF=90\degree, DE=5, DF=3$ をみたしているとき、線分 $BD$ の長さを求めよ。
答: $\frac {21\sqrt 2} 8$

後半最初はまた幾何の問題で、図が付いてないので自分で描かないといけません。しかし、描いてイメージするのは比較的簡単な図面になっています。直角が2か所あるのをどう活かすか、という予感がします。

さて、このような場合、なんとなく垂線を引いてみたくなるものでしょう。 $E,F$ からそれぞれ辺 $BC$ へ下した垂線の足を $P,Q$ とします。
そうすると、元が直角二等辺三角形なので、 $B,C$ の周りに新たな直角二等辺三角形 $QFB, PCE$ ができることになります。

そうすると、色の同じ線分 $BQ,FQ$ と $CP,EP$ の組はそれぞれ長さが等しいということになります。
今求めたいのは $BD$ の長さなのですが、これを利用すると、実は $BD=$ 折れ線 $FQD$ ( ついでに $CD=$ 折れ線 $DPE$ ) であることが分かります。

さて一方で、色々と直角があると「合計が90°」となるような角の組み合わせが出てきます。
そうすると、相似な直角三角形が出てくるわけで、今回は $\triangle QDF, \triangle PED$ の2つが該当します。この相似比が斜辺の長さの比で $3:5$ です。
ということは、先ほど出てきた折れ線同士もこの長さの比になる、つまり、折れ線 $FQD:$ 折れ線 $DPE=3:5$ と分かります。

先ほど、折れ線と $BD,CD$ の関係を突き止めていましたから、あわせて考えると、結局 $D$ は $BC$ を $3:5$ に内分する点だったということです。

ということで、直角二等辺三角形 $ABC$ の斜辺 $BC=7\sqrt 2$ と、 $BD=\frac {3BC} {3+5}$ から計算できる、 $BD=\frac {21\sqrt 2} 8$ が答えとなります。
…なんとなく、前半にあった第4問の幾何より簡単なんじゃないかと思いますが、まあそういうこともあるのでしょう。

第8問

問題: $a_1\lt a_2\lt \cdots\lt a_{2022}$ をみたす正の整数の組 $(a_1,a_2,\cdots,a\_2022)$ であって、
$a_1^2-6^2\ge a_2^2-7^2\ge\cdots\ge a_{2022}^2-2027^2$
が成り立つものはいくつあるか。
答: 10個

西暦の2022にちなんだ予選3問目となる問題ですが、今度は数列と言いますか、規則性を元に考える問題と言えそうです。

$\{a_k\}$ を数列と見た場合、単調増加な正整数の数列というのが前提なのですが、しかし与えられた条件を見るに、「増分」を大きく取ることができないようになっていることが分かります。つまり、1 や 2 と言った小さい幅でしか増加させられない公算が高そうだということです。
なので、この「増分」に着目して攻めていきます。

では早速、増分を $\{d_k\}$ として次のように定義します。これは正整数の数列となります。

$d_k=a_{k+1}-a_k~~(k=1,2,\cdots,2021)$

そうしておいて、問題の条件を書き換えます。

\begin{split} ~ & a_1^2-6^2\ge a_2^2-7^2\ge\cdots\ge a_{2022}^2-2027^2 \\ \Leftrightarrow & a_k^2-(k+5)^2\ge a_{k+1}^2-(k+6)^2~~(k=1,2,\cdots,2021) \\ \Leftrightarrow & a_k^2-(k+5)^2\ge (a_k+d_k)^2-(k+6)^2~~(k=1,2,\cdots,2021) \\ \Leftrightarrow & (a_k+d_k)^2-a_k^2\le (k+6)^2-(k+5)^2~~(k=1,2,\cdots,2021) \\ \Leftrightarrow & 2d_k a_k+d_k^2\le 2k+11~~(k=1,2,\cdots,2021) \\ \Leftrightarrow & a_k\le \frac {2k+11-d_k^2}{2d_k}~~(k=1,2,\cdots,2021) \\ \end{split}

$d_k$ が正整数であることを考えると、次のように上限が見積もれます。
※この上限は $d_k=1$ の場合になっています。

\begin{split} ~ & a_k\le \frac {2k+11-d_k^2}{2d_k}~~(k=1,2,\cdots,2021) \\ \Rightarrow & a_k\le \frac {2k+11-1^2}{2\cdot 1}=k+5~~(k=1,2,\cdots,2021) (\because d_k\ge 1) \\ \end{split}

ところで、 $\{a_k\}$ は単調増加な正整数の数列なので、ざっくりと $k\le a_k$ です。
つまり、一番上限が緩い $d_k=1$ の場合でも、 $a_k$ の取れる値は幅6しかないということです。
これにより、全ての $d_k$ が1となる、つまり $\{a_k\}$ が公差1の等差数列となるケースでも6通りしかありません。

$d_k=1~~(k=1,2,\cdots,2021)$ の場合
$a_k=k~(k=1,2,\cdots,2021), a_k=k+1~(k=1,2,\cdots,2021), \cdots, a_k=k+5~(k=1,2,\cdots,2021)$ の6通り

残りは、 $d_k\ge 2$ となる項が混じるケースです。
しかし $a_k\le \frac {2k+11-d_k^2}{2d_k}$ という条件を見るに、その項では不等式右辺の $k$ の係数が1を割ります。なので、かなり $k$ の範囲が狭くなるであろうことが想像できます。
それを調べるために、 $k\le a_k$ と組み合わせ、 $k\le\frac {2k+11-d_k^2}{2d_k}$ という条件を整理します。

\begin{split} ~&k\le\frac {2k+11-d_k^2}{2d_k} \\ \Leftrightarrow&2d_k k\le 2k+11-d_k^2 \\ \Leftrightarrow&2d_k k-2k\le 11-d_k^2 \\ \Leftrightarrow&k\le \frac{11-d_k^2}{2(d_k-1)} \\ \end{split}

この形を見るだけでも、 $d_k$ の取れる範囲は相当狭そうなので、順々に確かめていきます。

$d_k=2$ となる項がある場合
その項に対して $k\le\frac{11-2^2}{2(2-1)}=3.5$ 、すなわち $k=1,2,3$
$d_k=3$ となる項がある場合
その項に対して $k\le\frac{11-3^2}{2(3-1)}=0.5$ 、この条件を満たす $k$ は既に存在しない
$d_k\ge 4$ となる項がある場合
その項に対して、不等式右辺 $\frac{11-d_k^2}{2(d_k-1)}\lt 0$ なので、この条件を満たす $k$ は存在しない

なんともう、1以外の $d_k$ の値の候補は2しかなく、その項も $k=1,2,3$ に限られるということです。これをもう少し詳しく見てみます。 $k\le a_k\le \frac {2k+11-d_k^2}{2d_k}$ から、以下が分かります。

$d_1=2$ の場合
$1\le a_1\le\frac{2\cdot 1+11-2^2}{2\cdot 2}\Leftrightarrow 1\le a_1\le 2.25$
よって、 $a_1=1,2$ 次項とまとめると $(a_1,a_2)=(1,3),(2,4)$ このとき $4\le a_3$
$d_2=2$ の場合
$2\le a_2\le\frac{2\cdot 2+11-2^2}{2\cdot 2}\Leftrightarrow 2\le a_2\le 2.75$
よって、 $a_2=2$ 次項とまとめると $(a_2,a_3)=(2,4)$
$d_3=2$ の場合
$3\le a_3\le\frac{2\cdot 3+11-2^2}{2\cdot 2}\Leftrightarrow 2\le a_2\le 3.25$
よって、 $a_3=3$ 次項とまとめると $(a_3,a_4)=(3,5)$

整理された $a_1,a_2,a_3$ の値を見るに、それぞれのケースを同時に満たすことはできません。つまり、 $d_k=2$ となるのは1項のみ、他の項は $d_k=1$ です。
なので、 $(a_1,a_2)=(1,3),(2,4), (a_2,a_3)=(2,4), (a_3,a_4)=(3,5)$ の4通りがそのまま $\{a_k\}$ 4通りに対応します。具体的には、次の通りです。

$a_1=1, a_k=k+1~~(k=2,3,\cdots,2022)$
$a_1=2, a_k=k+2~~(k=2,3,\cdots,2022)$
$a_1=1, a_2=2, a_k=k+1~~(k=3,4,\cdots,2022)$
$a_1=1, a_2=2, a_3=3, a_k=k+1~~(k=4,5,\cdots,2022)$

これで全通り出揃いました。
$d_k=1~~(k=1,2,\cdots,2021)$ の6通りと、上の4通りを合わせ、答えは10通りとなります。

第9問

問題: $1,2,\cdots,1000$ の並び替え $(p_1,p_2,\cdots,p_{1000})$ であって、任意の1以上999以下の整数 $i$ に対して、 $p_i$ が $i$ の倍数であるようなものはいくつあるか。
答: 504個

ここらへんになると初見でなかなか掴みどころが無くなってきます。しかし、扱う数が1～1000となると、なんらか規則性を見つけて小さな問題に落とし込む手腕を発揮せざるを得ないところかと考えます。

まず、並び替えとありますが、順番そのままの $p_i=i~(i=1,2,\cdots,1000)$ も条件を満たします。これをベースラインにして色々いじってみることにします。
そうすると、 $p_{1000}$ については条件がないので1000が浮いていることになるのと、それ以外では「 $p_i$ が $i$ の倍数」という条件から $i\ge p_i$ が必要と、ベースライン以上の大きさの数をそれぞれ用意する必要があるということから、大きな数が決まったら選択の余地なく一気に他も決まるという感触があります。

具体的に見てみましょう。浮いている1000をどの $p_i$ に割り当てるか考えてみます。
$p_{1000}$ に割り当てるか、またそれ以外だと「1000のいずれかの約数 $i$ に対して $p_i=1000$ 」とする必要があります。
つまり、
$p_1=1000~~or~~p_2=1000~~or~~p_4=1000~~or~~p_5=1000~~or~~p_8=1000~~or~~p_{10}=1000~~or~~p_{20}=1000~~or~~p_{25}=1000~~or~~p_{40}=1000~~or~~p_{50}=1000~~or~~p_{100}=1000~~ or~~p_{125}=1000~~or~~p_{200}=1000~~or~~p_{250}=1000~~or~~p_{500}=1000~~or~~p_{1000}=1000$
と、候補は16通りです。ここで、

$p_{1000}=1000$ の場合
残り $1\sim 999$ を $i\ge p_i$ となるように $p_1\sim p_{999}$ に割り当て、ということなので、並び替えのない $p_i=i~(i=1,2,\cdots,999)$ しかありません。つまり、残りの割り当てが1通りに確定します。
$p_{1000}\ne 1000$ の場合
- 例えば $p_{200}=1000$ の場合
  未割当の $p_{201}\sim p_{999}$ に対して、使える大きな数が丁度 $201\sim 999$ しか残ってません。
  つまり、 $p_i=i~(i=201,202,\cdots,999)$ が確定し、 $1\sim 200$ を $p_1\sim p_{199}$ に割り当てる部分が未確定な分として残ります。
  ※余った1個は $p_{1000}$ に割り当てます。
- 例えば $p_{10}=1000$ の場合
  未割当の $p_{11}\sim p_{999}$ に対して、使える大きな数が丁度 $11\sim 999$ しか残ってません。
  つまり、 $p_i=i~(i=11,202,\cdots,999)$ が確定し、 $1\sim 10$ を $p_1\sim p_{9}$ に割り当てる部分が未確定な分として残ります。
  ※余った1個は $p_{1000}$ に割り当てます。

ここで着目したいのは、 $p_{1000}\ne 1000$ でそれぞれ「未確定な分」として残ったところです。
元々の問題が「 $p_1\sim p_{999}$ に $1\sim 1000$ を割り当てろ(余った1個は $p_{1000}$ へ)」だったところ、 $p_{200}=1000$ なら「 $p_1\sim p_{199}$ に $1\sim 200$ を割り当てろ」 $p_{10}=1000$ なら「 $p_1\sim p_{9}$ に $1\sim 10$ を割り当てろ」と、元の問題の規模縮小版が残っていることになるからです。
とすると、これを利用して再帰的に条件をまとめることができます。

そのため、次のように、正整数 $n$ に対して $f(n)$ を定義します。

$f(n)=1\sim n$ を各 $p_i$ が $i$ の倍数になるように $p_1\sim p_{n-1}$ に割り当てる(1つ余らせる)割り当て方の総数

そうすると、この $f(n)$ は次のような性質を持つことが分かります。

(この問題の答え) $=f(1000)$
( $p_{200}=1000$ と割り当てた場合の残りの割り当て方の総数) $=f(200)$
( $p_{10}=1000$ と割り当てた場合の残りの割り当て方の総数) $=f(10)$
…

加えて、

$f(1000)=f(1)+f(2)+f(4)+f(8)+f(10)+f(20)+f(25)+f(40)+f(50)+f(100)+f(125)+f(250)+f(500)+1$

と、より小さな数での $f$ の値にブレークダウンする方法と、

$f(n)=(\sum_{1\le i\lt n,~iはnの約数} f(i)) +1$ ( 特に $f(1)=1$ )

という、これを一般化した漸化式が分かります。

では、ここからはこの漸化式を元に計算を進めていくわけですが、最終的な目標が $f(1000)$ なので、途中で出てくる $f(i)$ の $i$ の部分は、全て1000の約数になるはずです。
1000の持つ素因数は2,5の2種類なので、約数-倍数の関係を2次元的に表して整理することができます。ちょうど次の図のようになります。

漸化式については、次の図のように可視化できます。

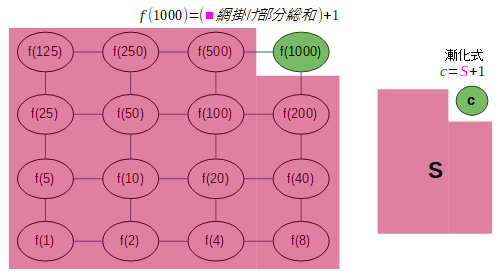
なお、漸化式の形からして縦横の扱いが等価なので、縦横を逆にしても同じ値になることが分かります。
とは言え、このままだと足し算する項目が少し多くなるので、次の図のように少しだけ簡略化しておきます。
※もっと整理することは可能ですが、あくまで $f(1000)$ が計算できる程度に楽になれば良いので、ここはあまり頑張りません。

あとは、 $f(1)=1$ から始めて、順々に値を埋めていくことになります。
まず、一番下の段ですが、下からの加算分がないので、単純に倍々していくのと同じことになります。

次に下から二番目の段ですが、先に「縦横を逆にしても同じ値」ということを利用して、一番左の列を埋めておきます。その上で、漸化式を適用していきます。

その後同様に計算していきます。

最終的に、図の右上の隅、 $f(1000)$ の値は504と計算でき、これが答えとなります。

第10問

問題: 1以上50以下の整数から相異なる25個の整数を選ぶ方法であって、選ばれたどの相異なる2つの整数についても、一方が他方の約数となることがないようなものは何通りあるか。
答: 1632通り

「何通り」と言われても、これも問題を見て途方にくれる問題です。しかし、解けるようにできている問題である以上、なにかポイントがあるはずで、そこに辿り着けるよう条件を整理していくところに気を使う問題かと思います。

問題となるのは「選ばれたどの相異なる2つの整数についても、一方が他方の約数となることがない」という条件です。
例えば、1～25の25個を選んだ場合、(1,2),(1,3),…や(5,25)といった「一方が他方の約数になる」という2つの整数の組み合わせが含まれるので、条件を満たしません。
24～48の25個でも(24,48)という組が含まれるので、やはり満たしません。
ところが、26～50の25個であれば、そういう組がないので条件を満たすことになります。
ここから、25個の中にある整数を採用したら、例えば14であれば、その約数である1,2,7、倍数である28,42、これら約数・倍数は採用できなくなるということが分かります。

しかし、「約数・倍数が採用できない」と言っても、では色々な選択肢がある中25個をどう選んでいくのか。割と途方に暮れるところです。なので、ここでちょっと単純化してみます。
約数・倍数の関係には推移性があり、例えば×3倍の関係に限定すると、次の45を先頭にする例のような系列を作ることができます。
※45の約数で9とか、15の倍数で30とか、5の約数で1とか、他にも倍数・約数になる数あるじゃないか、という考えは一旦押し込めておきます。あくまでここでは×3倍に着目している、ということです。

この系列の中でどの整数を採用するか考えてみると、そもそもどれも採用しないというパターンもありますが、どれか1つを採用するなら倍数・約数の関係にある他の数は自動的に不採用です。
つまり、系列中多くても1つしか採用できないということになります。

と、このように「系列」という考え方を準備しておいて、実際に1～50の数を×2倍の関係に着目して系列に分けてみます。そうすると、26～50の25個を先頭にした25系列ができるはずです。
※49,47等の奇数だと、×2倍の関係にある数がありませんが、それはそれで1個の数のみでの系列としておきます。

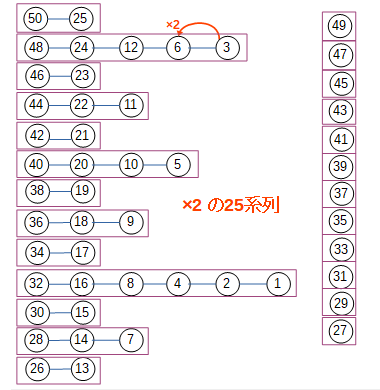
ここでやっと、問題で「25個」となっていた意図に気付きます。
1系列につき高々1個しか整数を採用できないので、25系列だと実はギリギリのところになっていて全系列から1個ずつ採用する以外にないということになるのです。
これで、一挙に選択肢を狭めることができました。以降、この系列に基づいて考えていきます。

まず、1個しか整数を含まない系列は、自動的に全部採用が決まります。
これは、27,29,…,49の奇数が該当します。
同時に、それらの約数である1,3,…,15の奇数は不採用となります。

続いて、不採用の数が出たことで、新たに30,26の2系列では、1個しか整数が残りません。なので、ここも自動的に採用が決まります。
※先ほど不採用が決まった数は、図からは既に取り除いています。
同時に、その約数である偶数2,6,10も不採用となります。( 奇数は既に不採用なので偶数のみ着目 )
ついでに4の不採用も決めておきます。6が不採用になったことで、48の系列の残りは全て4の倍数であって、4を採用するとこの系列自体が死んでしまうからです。

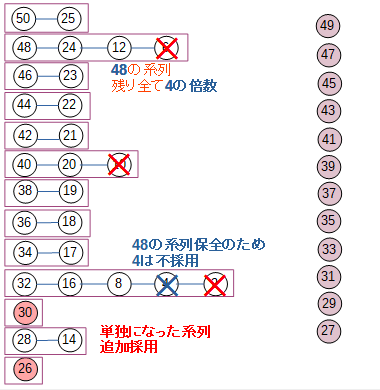
これで、14個が採用済みとなり、残り11系列をどうするか、というところまで整理できました。
ということで、残りを個別に見ていくことにします。

50,46,44,38,34の5系列
各系列、2個の整数があるのですが、どちらを選んでも他の系列の選択に影響を与えません。
つまり、それぞれ独立で完全に2択として考えて良いということになります。
そのため、ここの部分だけで $2^5=32$ 通りになります。
42,28の2系列
他の系列への影響はないのですが、この2系列間で、42が14の3倍という約数・倍数の関係があるため、上の5系列のような完全2択ではありません。
しかし逆に言えば、その(42,14)の組だけ除外すれば済むので、 $2^2-1=3$ 通りとして計算できます。
48,40,36,32の4系列
この残り4系列の間には、×3倍、×5倍といった約数・倍数の関係があり、それなりに干渉しあいます。そのため、個別に状況を見る必要があります。が、それらの状況を合算すると17通りになることが分かります。
- 8を採用する場合
  連鎖的に8,12,18,20の採用が決まりますので、この場合は1通りのみです。
- 8不採用、12採用の場合
  18は決定しますが、残った32,40の2系列は完全に2択です。そのため $2^2=4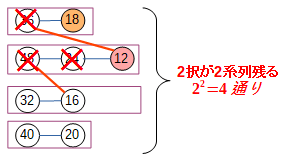$ 通りです。
- 8,12ともに不採用の場合
  36,40の2系列が独立していて完全に2択、48,32の2系列は(48,16)のみ除いて3通りです。そのため、 $2^2\times 3=12$ 通りです。