Zenn
🏅

日本数学オリンピック(JMO)2024年予選解答私的解説 その2

2024/01/25に公開
math
#
jmo
#
数学オリンピック
tech

はじめに

背景

さる2024年1月8日(月,祝)実施された、第34回日本数学オリンピック予選の解説の続きです。

参考情報

解説

それでは、今回の「その2」では、第7問～第10問の4問を解説していきます。

第7問

  • 問題: 次の条件をみたす3以上の素数pと1以上2024以下の整数aの組(p,a)の個数を求めよ。
    a\lt p^4であり、ap^4+2p^3+2p^2+1が平方数となる。
  • 答: 16個

後半最初はなにやら計算を頑張る必要がありそうな問題です。取り敢えずmodを見て条件を整理するのが鉄板そうに見えるので、その路線で攻めていきます。

まず平方数という条件がありますから、次のような整数 r\gt 0 を導入しておきます。

  • r^2=ap^4+2p^3+2p^2+1 …①

そして、modを見る前に大きさを見積もっておきます。
aの大きさの条件として 1\le a\le p^4-1 なので、この最小・最大での様子を精査しておきます。

  • 最小 ( a=1 )
    r^2=p^4+2p^3+2p^2+1 から大きさを見積もります。
    ※実際にa=1となるかは気にしません
    • (p^4+2p^3+2p^2+1)-(p^2+p)^2=p^2+1\gt 0
    • (p^2+p+1)^2-(p^4+2p^3+2p^2+1)=p^2+2p\gt 0
    • 以上より、(p^2+p)^2\lt p^4+2p^3+2p^2+1\lt(p^2+p+1)^2
  • 最大 ( a=p^4-1 )
    r^2=p^4(p^4-1)+2p^3+2p^2+1 から大きさを見積もります。
    ※実際にa=p^4-1となるかは気にしません
    • (p^4(p^4-1)+2p^3+2p^2+1)-(p^4-1)^2=p^4+2p^3+2p^2\gt 0
    • (p^4)^2-(p^4(p^4-1)+2p^3+2p^2+1)=(p-3)(p^3+p^2+5p+15)+44\gt 0~~\because p\ge 3
    • 以上より、(p^4-1)^2\lt p^4(p^4-1)+2p^3+2p^2+1\lt(p^4)^2

これで最小・最大での大きさを細かく見積もりましたので ( 他の条件があるという前提のもと ) 1\le a\le p^4 は次の同値な条件に置きかえることができます。

  • p^2+p+1\le r\le p^4-1 …②

そうしておいて、いよいよmodの条件を見ていきます。

p が3以上の素数という条件と、① から r^2\equiv 1~\mod~p^2 \Leftrightarrow r\equiv \pm 1~\mod~p^2 です。
※単純に平方根とっていいの? と気になるかもしれませんが、r\equiv\pm 1 以外では、r^2\equiv 1\Leftrightarrow (r-1)(r+1)\equiv 0~\mod~p^2 と整理してr\equiv 1~\mod~p かつ r\equiv -1~mod~p、この2式の辺々引いて得られる 0\equiv 2~mod~p が不整合となりますから、解なしだと分かります。

話を戻して、\pm 1で2択になっているわけですが、場合分けを先送りするため新しく s,t を導入して次のような形で置いておきます。

  • r=tp^2+s,~~s=\pm 1~~~~(~s^2=1~) …③

これを改めて①に代入して更に整理します。

\begin{align*} &(tp^2+s)^2=ap^4+2p^3+2p^2+1 \\ &\Leftrightarrow p^2((t^2-a)p^2+2st-2(p+1))=1-s^2 \\ &\Leftrightarrow p^2((t^2-a)p^2+2st-2s^2(p+1))=1-1=0~~\because s^2=1 \\ &\Leftrightarrow (t^2-a)p^2+2s(t-s(p+1))=0 \\ &\Rightarrow t\equiv s(p+1)~\mod~p^2 \end{align*}

※何気なく2sで割っているように見えますが、mod~p^2 において 2s に逆数があることは一応確認が必要です。2s,~p^2 が互いに素なので、で十分なのですが、具体的に 2s\cdot\frac{s(p^2+1)}{2}\equiv 1~\mod~p^2 から逆数を出すこともできます。

以上から更に u を導入して t=up^2+s(p+1) の形にし、③と併せます。
r=tp^2+s=p^2(up^2+s(p+1))+s=up^4+s(p^3+p^2+1) です。改めて、

  • r=up^4+s(p^3+p^2+1),~~s=\pm 1~~~~(~s^2=1~) …④

また、上での式変形を (t^2-a)p^2+2s(t-s(p+1))=0 から続けていきます。

\begin{align*} &(t^2-a)p^2+2s(t-s(p+1))=0 \\ &\Leftrightarrow ((up^2+s(p+1))^2-a)p^2+2s(up^2+s(p+1)-s(p+1))=0 \\ &\Leftrightarrow p^2((up^2+s(p+1))^2-a-2us)=0 \\ &\Leftrightarrow a=(up^2+s(p+1))^2+2us=u^2p^4+s^2(p+1)^2+2us(p^3+p^2+1) \\ \end{align*}

以上より、aの形が確定し、平方数という条件が吸収されました。

  • a=u^2p^4+(p+1)^2+2us(p^3+p^2+1) …⑤

さて、s,u という2パラメータが絡むわけですが、実は大きさの条件を精査するとほとんど選択肢がありません。

  • p^2+p+1\le r\le p^4-1 …②
  • r=up^4+s(p^3+p^2+1),~~s=\pm 1~~~~(~s^2=1~) …④

再掲したこの2条件を改めて見ると、u が1変化するだけでrにp^4の変化が出て②の条件から外れますから、(s,u)=(1,0),(-1,1) 以外にありません。念のため②の下限の条件を吟味しておきます。
p\ge 3を考慮し、以下のように確認できます。

  • (s,u)=(1,0) のとき r=p^3+p^2+1 より r-(p^2+p+1)=p^3-p=p(p^2-1)\ge 0
  • (s,u)=(-1,1) のとき r=p^4-(p^3+p^2+1) より
    r-(p^2+p+1)=p^4-p^3-2p^2-p-1=(p-3)(p^3+2p^2+4p+11)+32\ge 0

ということで、最終的に⑤に(s,u)の値を適用し、以下の2パターンが残ります。

  • (s,u)=(1,0) のとき、a=(p+1)^2
  • (s,u)=(-1,1) のとき、a=p^4+(p+1)^2-2(p^3+p^2+1)=p^4-2p^3-p^2+2p-1

この中で a\le 2024 を満たすのは、前者だと p=3,5,7,\cdots,43 という、43以下の奇素数13通り、後者だと p=3,5,7 の3通りです。なので、(p,a) の組は合わせて16個であり、これが答えになります。

ちょっと途中式の形が面倒に見えますが、信じて計算を続ければ、という感じの問題でした。

第8問

  • 問題: 非負整数に対して定義され整数値をとる関数fが、任意の非負整数m,nに対して
    f(m+n)^2=f(m|f(n)|)+f(n^2)
    をみたしているとき、整数の組(f(0),f(1),\cdots,f(2024))としてありうるものはいくつあるか
  • 答: 2^{990}+1個

今度は整数の関数の問題です。取り敢えずよく分からないところですが、小さなm,nから調べていって全体を探るという地道な方法で行くことにします。

まず、定番として m=n=0 のケースを考えます。
このとき f(0)^2=2f(0) ですから、f(0)=0,2 がすぐに分かります。ということで、ここで2択が発生します。
ただ、f(0)=0 であれば n=0 のケースを考えることで f(m)^2=0 が導き出されますから、これは定数関数 f(x)=0 しかありえません。( 逆に定数関数 f(x)=0 であれば任意のm,nで条件を満たすという十分条件も分かります )

ということで、残りとして f(0)=2 で考えていきます。n=0~or~m=0 のケースを整理して次の2条件が分かります。

  • f(m)^2=f(2m)+2 …①
  • f(n)^2=f(n^2)+2 …②

ついでに、①のmをnに置きかえると、左辺が②と一致していますから、右辺同士を比べて次のことも分かります。

  • f(n^2)=f(2n) …③

更に②でn=1のケースも考えます。
すると、f(1)^2=f(1)+2 という2次方程式になっていますから f(1)=-1,2 とまた2択になっています。
ところが、f(1)=-1 だとすると m=n=1 の場合に f(2)^2=2f(1)=-2\lt 0 となりますから、f が整数値を取るという条件に反します。ですので、実は2択ではなく f(1)=2 と一通りに決まっています。

大分煮詰まってきたところで、今度は n=1 ( mは任意 ) のケースを考えます。

  • f(m+1)^2=f(2m)+2 …④

よく見ると、これは①と右辺の形が同じです。これより f(m+1)^2=f(m)^2 とかなり決定的な条件が得られます。これで数学的帰納法により f(x)^2=f(0)^2 すなわち |f(x)|=2 が導かれるからです。
後は①,③から f(n^2)=f(2n)=f(n)^2-2=2 です。
改めてまとめると、偶数または平方数のxでf(x)=2、それ以外で|f(x)|=2 です。
このとき、f(m+n)^2-(f(m|f(n)|)+f(n^2))=2^2-(f(2m)+f(n^2))=2^2-(2+2)=0 ですから元の条件 f(m+n)^2=f(m|f(n)|)+f(n^2) を十分満たします。

以上でfの形が明らかになりました。最終的に求めるのは整数の組(f(0),f(1),\cdots,f(2024))の個数ですから数えていきますと、

  • 定数関数 f(x)=0 の場合
    全て 0 の組で 1個
  • |f(x)|=2、xが偶数または平方数の時に限りf(x)=2 の場合
    1\sim 2024 の中の奇数 1012個から、平方数 1^2,3^2,5^2,\cdots,43^2 の22個を除いた990個のxに対してf(x)=\pm 2 で 2^{990}個

この合計で 2^{990}+1個が答えとなります。条件を漏らさぬよう注意すればなんとかなる、という感じでしょうか。

第9問

  • 問題: 円に内接する四角形ABCDがあり、AB=7,~BC=18をみたしている。\angle CDAの二等分線と辺BCが点Eで交わっており、また線分DE状の点Fが\angle AED=\angle FCDをみたしている。BE=5,~EF=3のとき、線分DFの長さを求めよ。
  • 答: \frac{17}{3}

こちらが最後の図形問題になりますが、例によって図は示されていません。
そこでどのように図を描いていくか、というところですが、問題文にある全条件を盛り込むと次図左のようになるところ、CBとDAを延長した交点 ( Pとする ) を導入するのが決め手になります。

なお、図の上側 ( A,Bの側 ) ではなく下の方に交点ができる可能性はないの? と気になるところではありますが、計算してみると長さの条件で不整合が起こるため、可能性無しとして除外できます。( 詳細は割愛します )
ついでに、各線分の長さとして DE=x,~PB=y,~PA=p,~AD=q,~CD=r を導入しておきます。
こんなに文字をたくさん使って収拾付くか心配かも知れませんが、意外となんとかなります。

このようにすることで、次図のように円に内接する四角形に関連した相似形と、角の二等分線による長さの比の条件と、両方活かすことができ、一石二鳥なのです。

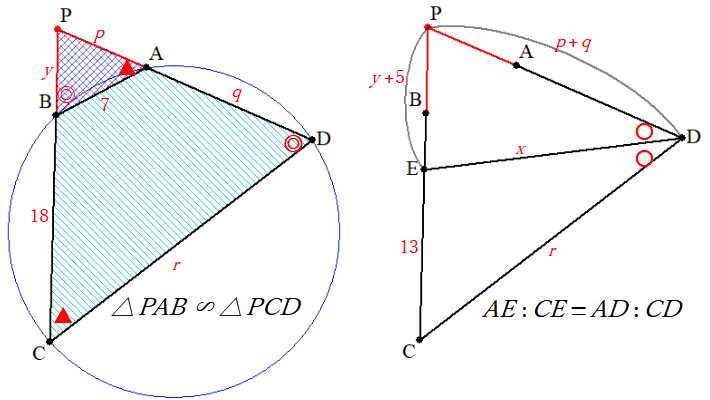
すなわち、左側を見ると、四角形が円に内接していることから \angle PBA=\angle D,~\angle PAB=\angle C ( 図中の◎同士▲同士 ) であり、\triangle PAB\sim \triangle PCD が、
右側を見ると、\angle D の二等分線から長さの比 AE:CE=AD:CD がそれぞれ分かるということです。

前者から PB:AB=PD:CD\Rightarrow y:7=p+q:r、
後者から y+5:13=p+q:r の2つの比が分かり、しかも両者ともp+q:r が共通ですから、ここから y:7=y+5:13 であり、これを解いて y=\frac{35}{6} が分かります。

改めて比を整理すると、p+q:r=5:6 ですから、分数でごちゃごちゃするのを避けるため a=\frac{13}{6} と置いた上で、p+q=5s,~r=6s とします。
その上で、更に相似と角の二等分線を活用します。

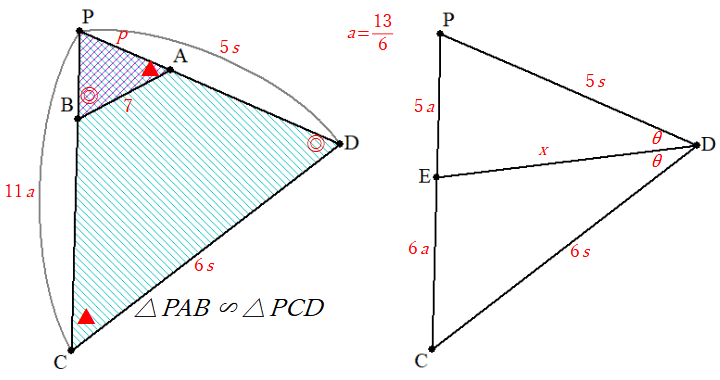
左側、相似の別の条件として PA:AB=PC:CD\Rightarrow p:7=11a:6s これより 6ps=77a です。
今度、右側は等しい角を\thetaと置いて余弦定理を適用します。

\begin{align*} x^2+(5s)^2-(5a)^2-2\cdot x\cdot 5s\cdot \cos\theta&=0 \\ x^2+(6s)^2-(6a)^2-2\cdot x\cdot 6s\cdot \cos\theta&=0 \end{align*}

この2式の6倍・5倍を辺々差し引くことで \cos\theta が消去でき、x^2=30(s^2-a^2) が分かります。

最後に、今まで置き去りにしてきたF ( \angle FCD=\angle AED,~EF=3 ) を追加します。

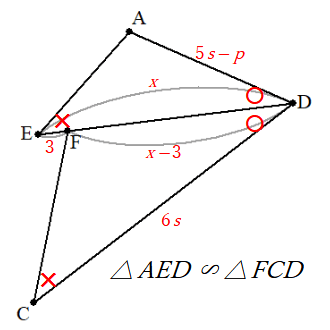
見るからに三角形の相似 \triangle AED\sim\triangle FCD ですから、AD:ED=FD:FC\Rightarrow 5s-p:x=x-3:6s ここから x^2-3x-30s^2+6ps=0 が分かります。

これで条件が出そろいました。改めて挙げると、次の3つです。

  • 6ps=77a
  • x^2=30(s^2-a^2)
  • x^2-3x-30s^2+6ps=0

すると都合の良いことに、x^2,~6ps を消すことで同時に s^2 も消えてくれます。
すなわち、3番目の式に1番目・2番目を代入して、

\begin{align*} ~&30(s^2-a^2)-3x-30s^2+77a=0 \\ \Rightarrow&-30a^2-3x+77a=0 \\ \Rightarrow&x=\frac{1}{3}\cdot a(77-30a) \end{align*}

a=\frac{13}{6} と置いていましたから、計算して x=\frac{26}{3} です。
最終的に求めるのは DF=x-3 ですから、答えは \frac{17}{3} となります。 最初のPの導入がとにかく大事なところでした。

第10問

  • 問題: 100×100のマス目の各マスにJ,M,Oのいずれか1文字を書き込むことを考える。2×2のマス目であって次のいずれかをみたしているものを良いブロックとよぶこととする。

    • その4マスに書き込まれた文字がちょうど1種類である。
    • その4マスに書き込まれた文字がちょうど2種類であり、その2種類の文字はそれぞれ2つずつ書き込まれている。
    • その4マスに書き込まれた文字がちょうど3種類であり、左下と右上のマスに同じ文字が書き込まれている。

    このとき、次の条件をともにみたすような書き込み方はいくつあるか。

    • どの2×2のマス目も良いブロックである。
    • 辺を共有して隣りあう2マスの組であって書き込まれた文字が異なるものはちょうど10000組存在する。ただし、マスの順番を入れ替えただけの組は同じものとみなす。

    ただし、回転や裏返しによって一致する書き込み方も異なるものとして数える。

  • 答: ~_{198}C_{100}\cdot 3\cdot 2^{100}通り

いよいよ2ケタ台の問題です。最後の程難しくなる傾向に違わず、問題文を眺めただけではさっぱり方針が立ちません。そもそも 100×100 なんて描いて細かく調べる気にもなりません。

取り敢えず、手がかりである良いブロックがどんなものであるか、そこから把握することにしましょう。列挙すると次図のような5パターンになるはずです。

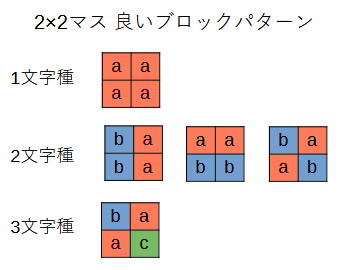
これでもまだ見えてこないのですが、ふと2×1のマスが同じ文字の場合を想像してみます。

そうすると上の図の通り、同じ文字の2×1のマスが続くことになりますから、もし異なる文字のマスの間に境界線を引いた場合、境界線が途中で途切れることなく端々でつながることになります。
しかも、これは縦横入れ替えても成り立つ話です。ということは、次図のようにマス全体が端々の境界線で区画に分けられると分かります。

これで大分見通しが良くなりました。
続いて「辺を共有して隣りあう2マスの組であって書き込まれた文字が異なるものはちょうど10000組存在する」という条件を思い出します。

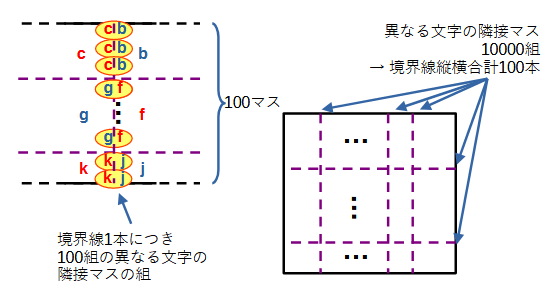
区画の境界線は ( 全体が100×100マスであるため ) 1本あればその側に100組の文字の異なる隣接マスの組ができます。そのため境界線が縦横合わせて100本あると分かります。
そうしましたら、もう少し「良いブロック」の条件を精査します。具体的には次の図のように縦横の境界線の交差点付近の状況に着目します。

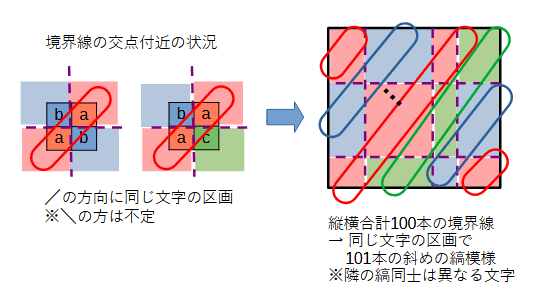
境界線を挟んで異なる文字のマスが隣り合ってる部分ですから、2文字種のクロスか3文字種のブロック状況に絞られますが、いずれも／の方向に同じ文字種の区画が続くことになります。ということは、全体では縦横合わせて100本の境界から、同じ文字種の区画が斜めの縞模様として101本分できると分かります。
しかも、これは縦横の境界線の本数の内訳に依りません。

これで状況が整いました。
使える文字種は J,M,O の3種だけなので、片方の端の縞が3通り、そこから次々隣の縞を決めていくのは各2通りで、3\cdot 2^{100}通りの選び方があります。
これは、境界線の配置を固定した時の話で、実際は縦横99か所ずつ計198か所に100本の境界線を配置しますから、更に~_{198}C_{100}倍されます。
そのため、最終的な答えは ~_{198}C_{100}\cdot 3\cdot 2^{100}通りと計算できます。

境界線のことに気付けば、一気に見通しが明るくなる問題でした。

おわりに

ということで、難易度の上がった後半の4問分を解説しました。
状況を整理できればなんとかなるところではないでしょうか。残りは ( おそらく ) 最難関の2問です。

Discussion