日本数学オリンピック(JMO)2024年予選解答私的解説 その3(完)
はじめに
背景
さる2024年1月8日(月,祝)実施された、第34回日本数学オリンピック予選の解説の最後となります。
参考情報
- その1 … https://zenn.dev/angel_p_57/articles/7375a989e85be2
- その2 … https://zenn.dev/angel_p_57/articles/f0dd1569d85f56
- 問題公開先 … https://www.imojp.org/archive/mo2024/problems/jmo34yqa.pdf
解説
それでは、最後に第11問・第12問の2問を解説していきます。
第11問
- 問題: 正の整数に対して定義され正の整数値をとる関数
f f(34)=2024 a,b,c
a+f(b),~~b+f(c),~~c+f(a)
であるような三角形が存在する。このとき、f(100)+f(101)+\cdots+f(199) - 答: 102050
関数の問題第二弾です。しかし、かなり条件がふわっとしている上、小さい数のところから値を決めていくようなこともできません。
取り敢えず三角形が存在するという条件くらいしか手がかりがありません。なのでそこから考えていくことにします。つまり、
※なお、問題文にある「ただし、同一直線上にある3点は三角形をなさないものとする」は、三角不等式の不等号
この三角不等式がどの辺の長さの順番でも成立することが必要十分です。そのため、この3条件になるのですが…
(a+f(b))+(b+f(c))\gt (c+f(a)) (b+f(c))+(c+f(a))\gt (a+f(b)) (c+f(a))+(a+f(b))\gt (b+f(c))
実はこの3条件、全て同じ内容を表しています。なぜかというと、
改めて次のように条件を列挙し直します。なお、整数という条件は大前提として省略し、また不等号
f(x)\ge 1 f(34)=2024 x+f(y)+y+f(z)\ge z+f(x)+1
この最後の条件を色々いじることになります。実際裏では色々なパターンを試して使えそうなものを厳選していたわけですが、ここでは既に選び終わったものをご紹介します。
-
x=y=1 1+f(1)+1+f(z)\ge z+f(1)+1\Leftrightarrow f(z)-z\ge-1 -
y=z=1 x+f(1)+1+f(1)\ge 1+f(x)+1\Leftrightarrow f(x)-x\le 2f(1)-1
これで分かることは、
そのため、ここからは
-
g(x)+x\ge 1\Leftrightarrow g(x)\ge 1-x -
g(34)+34=2024\Leftrightarrow g(34)=1990 -
x+(g(y)+y)+y+(g(z)+z)\ge z+(g(x)+x)+1\Leftrightarrow g(y)+2y+g(z)\ge g(x)+1 -
L,U~s.t.~-1\le L\le U x_L,x_U~s.t.~g(x_L)=L,g(x_U)=U L\le g(x)\le U
④で出てくる
さて。最小・最大を導入したことで、実はとても大きなメリットが生じています。それは任意の~が前提となっている条件を最悪のケースのケアだけで置き換えることができることです。
すなわち、③がこう変わります。
-
g(y)+2y+g(z)\ge g(x)+1\Leftrightarrow g(y)+2y+L\ge U+1\Leftrightarrow U-L+1-2y\le g(y)
あとは、②の
- ④より
L\le g(34)\le U L\le 1990\le U - ③'より
U-L+1-2\cdot 34\le g(34) U\le L+2057
おまけですが、① の
※実際
これでようやく
g(34)=1990 -
L,U~s.t.~-1\le L\le 1990\le U\le L+2057
x_L,x_U~s.t.~g(x_L)=L,g(x_U)=U L\le g(x)\le U U-L+1-2x\le g(x)
なお、詳細は割愛しますが
では長かったですが、ここからが本題です。
求めるのは
そうすると、まず
そのため
このとき、
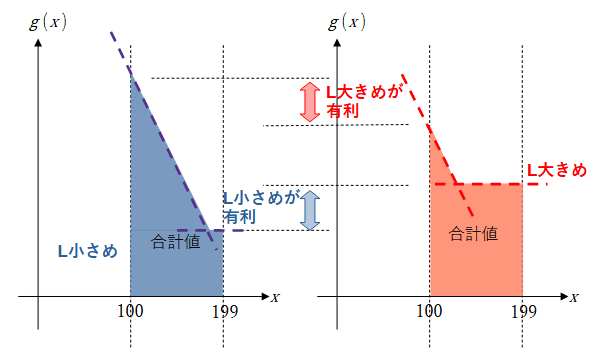
まあそうすると半々くらいがちょうど良くね? と思ったりもするのですが、そこは計算で確かめていきましょう。
そうすると、
※どちらかのパートが0項になっている状況も含みます。
1 で始まる公差2の等差数列の和
g(100)+g(101)+\cdots+g(199)=100L+(896-L)^2
ということで展開して平方完成なりして計算すると、確かに半々の状況になる
※念のためですが、一例として
最後に
なんというか、粘り強く条件を詰めていく根気が求められる問題なのかな、という感じでした。
第12問
- 問題: 次の条件をみたす0以上2099以下の整数の組
(a_{1},a_{2},\cdots,a_{2100})
整数の組(b_{1},b_{2},\cdots,b_{2100}) i
a_i\equiv \sum_{gcd(j-i,2100)=1,~1\le j\le 2100} b_j~~(mod~2100)
となるものが存在する。ただし、右辺はj-i j b_j - 答:
2^{256}\cdot 3^{180}\cdot 5^{420}\cdot 7^{210}
※あるいは\frac{2100^{210}}{2^{164}\cdot 3^{30}}
ついに最終問題です。いかにも難しそうです。そして実際解くの大変です。
ここで誠に申し訳ないのですが、この解説を書くにあたり、線形代数(行列計算)の知識前提のものしかできませんでした。もしよく分からないという方は、解説中の用語を拾って線形代数の予習をしてから読み直してください。
なぜ線形代数が出てくるかというと、この問題が次のように書き換えられるからです。
- 問題の別表現
関数p(k) p(k)=1~~(~gcd(k,2100)=1~),~p(k)=0~~(~gcd(k,2100)\neq 1~) P=(P_{i,j})~~(~P_{i,j}=p(j-i)~) Z/2100Z {Z/2100Z}^{2100}
※任意の\bm b\in {Z/2100Z}^{2100} \bm a=P\bm b \bm a\in {Z/2100Z}^{2100} \{\bm a\}
なお、
で、この表現を見れば経験のある人は正則行列での変換なら全単射で次元数そのままだけど正則でなかったら次元が下がるヤツやとピンと来ることでしょう。実際そのような問題です。
なお、一旦注意事項として、問題では添え字を1~2100で扱ってますが、以降は様々な場面で添え字を0開始で扱うことにします。
例えば、線形変換
で、実はこの時点で分かることがあります。
それは
そうすると、行列
すなわち、
と210次正方行列
※なお、式中の例えば
そうすると、次の関係が成り立っていることが分かります。
ということは繰り返しになっている210次元分だけを調べれば済むということです。一気に次元が落ちました。
加えて、問題自体は mod 2100 での話ですが、これもより小さい数を法とする mod に分解して考えることができます。なぜなら、
これは要するに中国の剰余定理(CRT)の一例ということなのですが、ともかくmod 2100 で考える代わりに、mod 4, mod 3, mod 25, mod 7 での状況を組み合わせる ( 欲しいのは要素数なので、各 mod で調べた要素数を掛け合わせる ) ことで問題が解けることを意味します。
※もう少しちゃんと言うなら、
ということは、この問題は次の問題に置きかえることができることになります。
- 整理した問題
関数p(k) p(k)=0~~(~k が 2,3,5,7 いずれかの倍数~),~p(k)=1~~(~その他~) X=(X_{i,j})~~(~X_{i,j}=p(mod(j-i,210))~) Z/mZ m {Z/mZ}^{210} m=4,3,25,7
※m=4,3,25,7 \bm b\in {Z/mZ}^{210} \bm a=P\bm b \bm a\in {Z/mZ}^{210} \{\bm a\}
大分整理された気がしますが、実はここがスタートラインです。なぜなら依然として210次という巨大な行列が残っており、これを何とかして正則かどうか、正則でない場合どの程度次元が縮小されるかを調べなければならないからです。
もうこの形になった以上、個別のベクトル
ここで
- 第0行の要素並び
p(0),p(1),\cdots,p(k),\cdots,p(209) k
どういうことかと言うと、
0~209で全部書くのは大変なので、0~29 に限って並べ方を挙げると次のようになります。
0,6,12,18,24,10,16,22,28,4,20,26,2,8,14,15,21,27,3,9,25,1,7,13,19,5,11,17,23,29
ちゃんと数式で書くなら、次のような操作を行っていることになります。
- 優先順位を示す関数
s(k)
s(k)=mod(k,2)\cdot 105+mod(k,3)\cdot 35+mod(k,5)\cdot 7+mod(k,7) -
s(k) \sigma \sigma(k)=s^{-1}(k) - 行
(p(0),p(1),\cdots,p(k),\cdots,p(209)) (p(\sigma(0)),p(\sigma(1)),\cdots,p(\sigma(k)),\cdots,p(\sigma(209)))
こうすることで、次の図で示すように、段階的に先頭のブロックの要素が全て0、残りが同一パターンという規則性を作り出すことができます。
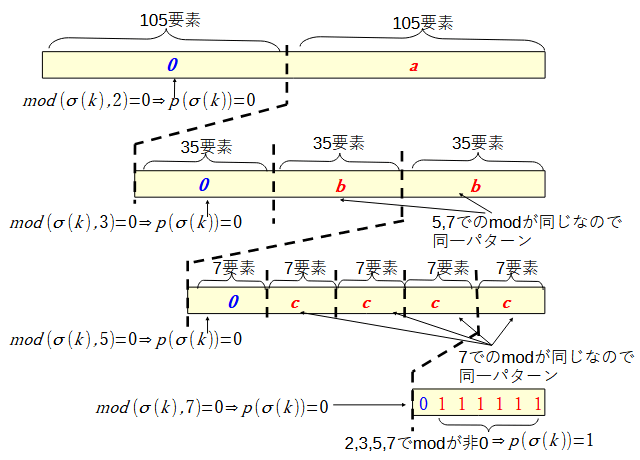
同じようなことを行同士の入れ替えとしても行います。
結局、行列全体で見れば、元の行列
そうすると、0の要素のブロックは対角部分に現れることになるため、
X'=\left(\begin{array}{c:c} ~ & A \\ \hdashline A & ~\end{array}\right) A=\left(\begin{array}{c:c:c} ~ & B & B \\ \hdashline B & ~ & B \\ \hdashline B & B & ~ \end{array}\right) B=\left(\begin{array}{c:c:c:c:c} ~ & C & C & C & C \\ \hdashline C & ~ & C & C & C \\ \hdashline C & C & ~ & C & C \\ \hdashline C & C & C & ~ & C \\ \hdashline C & C & C & C & ~ \end{array}\right) C=\left(\begin{array}{c:c:c:c:c:c:c} ~ & D & D & D & D & D & D \\ \hdashline D & ~ & D & D & D & D & D \\ \hdashline D & D & ~ & D & D & D & D \\ \hdashline D & D & D & ~ & D & D & D \\ \hdashline D & D & D & D & ~ & D & D \\ \hdashline D & D & D & D & D & ~ & D \\ \hdashline D & D & D & D & D & D & ~ \end{array}\right) -
D=(1)
これでようやく
実際、全要素が 1 のn次正方行列
そこで、rank を探るために地道に対角化を行うことにします。つまり、掃き出し法(ガウスの消去法)のように、行基本変形を繰り返し、なるべく対角行列に寄せていくということです。
ただ、定数倍だけは可逆操作 ( 正則行列の掛け算 ) にならないおそれがあるため避けます。
例えば、
※実際に手順を紹介すると長くなるので、正則行列を左から掛けることで同等の結果になるようにしています。
そうすると、最後の小行列ブロックに
-
X''=\left(\begin{array}{c:c} A & ~ \\ \hdashline ~ & A\end{array}\right) A'=\left(\begin{array}{c:c:c} B & ~ & -B \\ \hdashline ~ & B & -B \\ \hdashline ~ & ~ & 2B \end{array}\right) B'=\left(\begin{array}{c:c:c:c:c} C & ~ & ~ & ~ & -C \\ \hdashline ~ & C & ~ & ~ & -C \\ \hdashline ~ & ~ & C & ~ & -C \\ \hdashline ~ & ~ & ~ & C & -C \\ \hdashline ~ & ~ & ~ & ~ & 4C \end{array}\right) C'=\left(\begin{array}{c:c:c:c:c:c:c} D & ~ & ~ & ~ & ~ & ~ & -D \\ \hdashline ~ & D & ~ & ~ & ~ & ~ & -D \\ \hdashline ~ & ~ & D & ~ & ~ & ~ & -D \\ \hdashline ~ & ~ & ~ & D & ~ & ~ & -D \\ \hdashline ~ & ~ & ~ & ~ & D & ~ & -D \\ \hdashline ~ & ~ & ~ & ~ & ~ & D & -D \\ \hdashline ~ & ~ & ~ & ~ & ~ & ~ & 6D \end{array}\right)
そうすると焦点は、最後のブロックに現れる係数 2,4,6 が
-
m=25,7
係数2,4,6はいずれもZ/mZ X \{\bm a\}
ということで、\{\bm a\} 25^{210}, 7^{210} -
m=3
係数2,4にはZ/3Z 6\equiv 0~\mod~3 C' 6D=O
ということで、X 2\cdot 3\cdot 5\cdot 6=180 \{\bm a\} 3^{180} -
m=2
このケースが少し厄介です。なぜなら、係数2,4,6はいずれもZ/4Z 4\equiv 0~\mod~4 2x\equiv 0~\mod~4 x\not\equiv 0~\mod~4 - 0や零元が関わらない部分
行列を分解していく際に、最後の2B, 4C, 6D 2\cdot 2\cdot 4\cdot 6=96
これは丸々Z/4Z - 0になる部分
行列を分解していく際に、4C 2B, 6D 2\cdot 6\equiv 0~\mod~4
こちらは 50次元分 (2\cdot(3\cdot 7+4)=50 - 残り ( 零元が関わる部分 )
残り64次元分は、\bm{a}=X\bm{b} \bm{a'}=2R\bm{b'} R
そうすると、Z/4Z
以上を考慮すると、
\{\bm a\} Z/4Z 4^{96}\cdot 2^{64} - 0や零元が関わらない部分
以上で、各
正直に言うと、要素を並び替えて規則性を見出すことを思いつくまで相当時間がかかりました。これを本番試験の時間の中で解けたら人外レベルではないかと思います。
おわりに
今回で最後の2問も終わり、これで全部解説できました。
正直解く時よりも説明を書く方が大変だった気もしますが、皆さんの参考になれば幸いです。
来年ももし全問解ければ、また解説を挙げたいと思います。
Discussion