はじめに
背景
さる2024年1月8日(月,祝)実施された、第34回日本数学オリンピック予選につき、公開された問題を解いてみました。昨年は解けない問題があったので記事にするのを見合わせましたが、今年は一応全問解けたので、解説を挙げてみようと思います。
予選は全部で12問あり、前半と後半とでは大分難易度が違います。最初の方はあっさりと、後の方はややしっかりめにバランスを考え、3回くらいにわけて解説しようと思います。
参考情報
解説
それでは、今回の「その1」では、前半の6問を解説していきます。
第1問
- 問題: 以下の値は有理数である。これを既約分数の形で表せ。
\sqrt{\frac{123!-122!}{122!-121!}}
- 答: \frac{122}{11}
まずは第1問です。予想に反して西暦に関係ない普通の計算問題でした。
階乗が出てくるのにびびらず、共通部分を見出すことができれば次のように計算できます。
\begin{align*}
\sqrt{\frac{123!-122!}{122!-121!}}&=\sqrt{\frac{123\cdot 122\cdot 121!-122\cdot 121!}{122\cdot 121!-121!}} \\
~&=\sqrt{\frac{123\cdot 122-122}{122-1}} \\
~&=\sqrt{\frac{(123-1)\cdot 122}{121}} \\
~&=\sqrt{\frac{122^2}{11^2}} \\
~&=\frac{122}{11}
\end{align*}
まあ、ここはサクサク行きましょう。
第2問
2問目でついに西暦の2024にちなんだ問題の登場です。まあ、これ以降も出てくるのですが。
ここで出てくる「素敵な数」とは、結局どの桁も 2,3,5,7 のいずれかということで、候補をしらみつぶしに探してもそんなに大変ではありません。が、その中でできれば効率よく探したいところではあります。
まず、nを変数として直接使うより、x=n-34,~y=n+2024 として置いた x,y これらが素敵な数であるところから攻めていくことにします。
n を消去して y=x+2058 さらに y=x+2100-42 と変形すると桁同士を比較し易くなります。
※なぜかと言うと、-42 の計算で繰り下がりが発生しない ( 2-7が繰り下がりの発生するギリギリのケースなので、5以上の桁を含む数を引く形でないと繰り下がりになり得ない ) からです。
- 1の位に着目し、差が2となる桁の組み合わせはx,yの順で(5,3), (7,5)の2通り
- 10の位に着目し、差が4となる桁の組み合わせはx,yの順で(7,3)のみ
- 100の位に着目し、差が1となる桁の組み合わせはx,yの順で(2,3)のみ
以上より、(x,y)=(275,333), (277,335)が分かり、x=n-34 \Leftrightarrow n=x+34 から n=309, 311 が答えとなります。
第3問
- 問題: 一辺の長さが10の正三角形ABCがある。Aを通る円が辺BC(端点を除く)と点Xで接し、辺AB, ACとそれぞれAでない点D,Eで交わっている。BX\gt CX,~AD+AE=13がともに成り立つとき、線分BXの長さを求めよ。
- 答: 5+\sqrt{10}
ここで最初の図形問題です。何が有難いかと言うと、ちゃんと状況を問題の方で図示してくれているところです。
まあ、取り敢えず求めるべきところ BX=x と、あと一箇所 BD=y くらいおいて進めてみましょう。
この時、折れ線BAE=20, DAE=13 から CE=7-y が分かります。
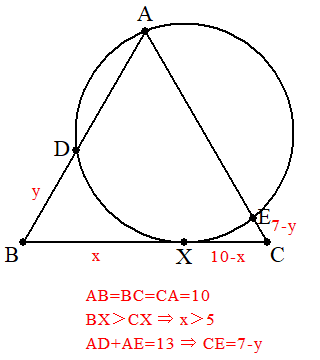
そうして、同じ色(赤/青)の線分を見てみます。
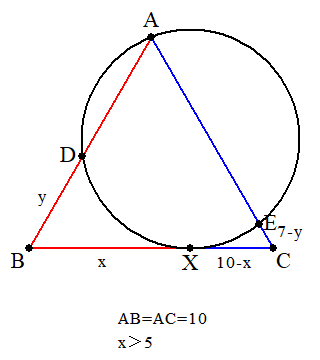
それぞれ、方べきの定理を適用できる形であり、
-
BD\cdot BA=BX^2 すなわち x^2=10y
-
CE\cdot CA=CX^2 すなわち (10-x)^2=10(7-y)
これで、x,yに関する連立方程式が立ちました。この2つの式を辺々足し合わせるとそのまま y が消えて x^2+(10-x)^2=70 という2次方程式が残ります。
詳細は省略しますが、x\gt 5 に注意して解くと、答え x=5+\sqrt{10} が得られます。
第4問
操作を行うことで、トータルの石の数が5^5\rightarrow 5^4\rightarrow 5^3\rightarrow 5^2\rightarrow 5^1\rightarrow 1 と変化していくわけなので、なんかとても規則性から数列的なものを考えてください、的な雰囲気を感じる問題です。
さて、なんとなくですが、数の少なくなるであろう白石を数えた方が楽な気がしますので、次のような数列を考えます。
- 数列\{w_k\}~(~k=1,2,3,\cdots~) を、黒白合計5^k 個から問題の操作を繰り返し、最後に残る1個の石が白石になるような最初の石の並べ方のある、白石の最小個数と定める。
こうすることで、
- 黒白合計5^k個での w_k-1 は、最初の石の並べ方によらず、最後に残る1個の石が必ず黒石である ( 最後に白石が残る並べ方がない ) ような白石の最大の個数である。
※1つ少なくなっていることに注意
というように、問題の条件を満たす白石の個数を考えているのと同じことになります。
実はここまで整理してしまえば、\{w_k\} については白石が3個ずつ組になるという最も効率の良い白石の残し方を考えることで、w_{k+1}=3w_k という漸化式が分かります。
明らかに w_1=3 なので、漸化式と併せて w_k=3^k です。
ということで、問題の黒石の個数 n については、全体 5^5 から最後に残る1個の石が必ず黒石であるような白石の個数 w_5-1 を引いて、 n=5^5-(w_5-1)=5^5-3^5+1=2883 と計算できます。これが答えです。
第5問
- 問題: 10以上の整数nであって、
[\frac n 1][\frac n 2]\cdots[\frac n {10}]=~_nC_{10}
をみたすようなもののうち、最小のものを求めよ。
- 答: 2519
ここで今までと毛色の違う問題が出てきました。なお、問題文中の [~] はガウス記号 ( 記号内の数を越えない最大の整数を表すもの ) です。
何にしてもそのままでは方針が立たないので、1～10の範囲になっているところを、例えば1～4の範囲に縮小して色々値を試してみます。
\begin{align*}
~&[\frac 8 1][\frac 8 2][\frac 8 3][\frac 8 4]&=8\cdot 4\cdot 2\cdot 2&=128~\gt~_8C_4&=\frac{8\cdot 7\cdot 6\cdot 5}{4\cdot 3\cdot 2\cdot 1}&=70 \\
~&[\frac 9 1][\frac 9 2][\frac 9 3][\frac 9 4]&=9\cdot 4\cdot 3\cdot 2&=216~\gt~_9C_4&=\frac{9\cdot 8\cdot 7\cdot 6}{4\cdot 3\cdot 2\cdot 1}&=126 \\
~&[\frac {10} 1][\frac {10} 2][\frac {10} 3][\frac {10} 4]&=10\cdot 5\cdot 3\cdot 2&=300~\gt~_{10}C_4&=\frac{10\cdot 9\cdot 8\cdot 7}{4\cdot 3\cdot 2\cdot 1}&=210 \\
~&[\frac {11} 1][\frac {11} 2][\frac {11} 3][\frac {11} 4]&=11\cdot 5\cdot 3\cdot 2&=330~=~_{11}C_4&=\frac{11\cdot 10\cdot 9\cdot 8}{4\cdot 3\cdot 2\cdot 1}&=330
\end{align*}
ただ、正直これだけだと「[~]を掛け合わせた方が大きそうだけどたまに等しくなる時もある??」くらいでまだまだよく分かりません。しかし、これを次のように整理すると途端に見通しがたちます。
\begin{align*}
~&[\frac {8} 1][\frac {8} 2][\frac {8} 3][\frac {8} 4]&=&\frac{\color{red} 8}{1}\cdot \frac{\color{red} 8}{2}\cdot \frac{\color{red} 6}{3}\cdot \frac{\color{red} 8}{4}&~\gt~_8C_4&=\frac{\color{red} 8}{1}\cdot \frac{\color{red} 7}{2}\cdot \frac{\color{red} 6}{3}\cdot \frac{\color{red} 5}{4} \\
~&[\frac {9} 1][\frac {9} 2][\frac {9} 3][\frac {9} 4]&=&\frac{\color{red} 9}{1}\cdot \frac{\color{red} 8}{2}\cdot \frac{\color{red} 9}{3}\cdot \frac{\color{red} 8}{4}&~\gt~_9C_4&=\frac{\color{red} 9}{1}\cdot \frac{\color{red} 8}{2}\cdot \frac{\color{red} 7}{3}\cdot \frac{\color{red} 6}{4} \\
~&[\frac {10} 1][\frac {10} 2][\frac {10} 3][\frac {10} 4]&=&\frac{\color{red} 10}{1}\cdot \frac{\color{red} 10}{2}\cdot \frac{\color{red} 9}{3}\cdot \frac{\color{red} 8}{4}&~\gt~_{10}C_4&=\frac{\color{red} 10}{1}\cdot \frac{\color{red} 9}{2}\cdot \frac{\color{red} 8}{3}\cdot \frac{\color{red} 7}{4} \\
~&[\frac {11} 1][\frac {11} 2][\frac {11} 3][\frac {11} 4]&=&\frac{\color{red} 11}{1}\cdot \frac{\color{red} 10}{2}\cdot \frac{\color{red} 9}{3}\cdot \frac{\color{red} 8}{4}&~=~_{11}C_4&=\frac{\color{red} 11}{1}\cdot \frac{\color{red} 10}{2}\cdot \frac{\color{red} 9}{3}\cdot \frac{\color{red} 8}{4}
\end{align*}
すなわち、分母を1,2,3,…の順番で揃える、ガウス記号の部分を整数でなく分数の形にしておくことで、並べて見ると各項の大小関係が見えてくるということです。
例えば最初のn=8の例なら、ガウス記号の積の分子部分は 8,8,6,8、C の式の方の分子部分は 8,7,6,5 で、各項で前者が後者以上となっています。最後の例ではじめて 11,10,9,8 同士等しくなっているくらいで、基本的に後者が前者が上回ることはないと推測できます。
実際、一般のnで確認してみると、
- ガウス記号の積
※なお、数式中のmod(n,k) はnをkで割った余りを、\prod は総積を表します
\begin{align*}
~&[\frac {n} 1][\frac {n} 2][\frac {n} 3][\frac {n} 4]\\ ~&=\frac{n-mod(n,1)}{1}\cdot\frac{n-mod(n,2)}{2}\cdot\frac{n-mod(n,3)}{3}\cdot\frac{n-mod(n,4)}{4}\\ ~&=\prod_{k=1}^4 \frac{n-mod(n,k)}{k}\end{align*}
\begin{align*}
~&~_nC_4\\ ~&=\frac{n-0}{1}\cdot\frac{n-1}{2}\cdot\frac{n-2}{3}\cdot\frac{n-3}{4}\\ ~&=\prod_{k=1}^4 \frac{n-(k-1)}{k}\end{align*}
このように整理すると、余りの性質 mod(n,k)\le k-1 と照らし合わせて、確かに後者が前者を上回ることがないこと、加えて全ての k で mod(n,k)=k-1 が成り立つ n=11 のところで等しくなっているのも尤もであることが分かります。
この等しくなる条件は n\equiv -1~~mod~k~(~k=1,2,3,\cdots) と書き換えることができますから、最小のnは n=LCM(1,2,3,\cdots)-1 ( LCMは最小公倍数を表す ) となります。
では問題に立ち戻ると、上の話の k=1,2,3,\cdots,10 の場合に相当しますから、最小のnは n=LCM(1,2,3,\cdots,10)-1 となります。登場する数の範囲的に素因数 2,3,5,7 の分に着目すれば十分なので、8\times 9\times 5\times 7-1=2519 と計算でき、これが答えとなります。
第6問
- 問題: AB=AC=5なる二等辺三角形ABCの辺AB上にAD=3をみたす点Dが、辺BC上(端点を除く)に点Eがある。点Eを通り直線ABに点Bで接する円を\omegaとすると、\omegaは三角形ADEの外接円に接した。\omegaと直線AEの交点のうちEでない方をFとすると、CF=10が成り立った。このとき、辺BCの長さを求めよ。
- 答: \frac{14\sqrt{65}}{13}
2つ目の図形問題です。が、図は描かれていません。適切に図を描けることができればそれだけ解に近づきますし、そういう能力が求められているんではないかと思います。
その際にコツと感じるのは、いきなり全体を問題文通りに描くのではなく、とっつき易いところから順々に拡張していくではないか、というところです。
この問題では、まず円\omega ( \triangle{BEF}の外接円 ) と、 \triangle{ADE}の外接円が接することから、点Eでの共通接線を引いて、辺ABとの交点をPとしておきます。
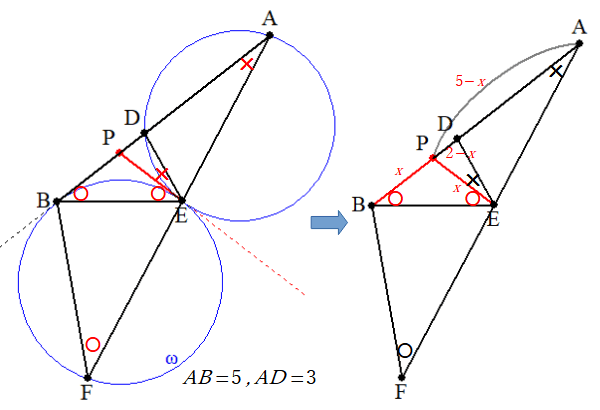
そうすると、三角形と外接円と円の接線の関係から、図中の〇同士✕同士の角の大きさが等しくなります。具体的には \angle BFE=\angle PBE=\angle PEB,~~\angle PAE=\angle PED です。
これで\triangle{PBE}が二等辺三角形と分かりますから、PB=PE=xと置いて、分かる範囲の長さを AD=5-x,~DP=2-x と整理しておきます。
続いて、✕の角の等しさを活かすため、三角形AEPに注目します。
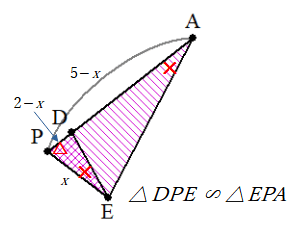
等しい角があれば相似形ができるのは世の常です。すなわち \triangle{DPE}\sim\triangle{EPA} です。
そのため、DP:PE=EP:PA\Rightarrow 2-x:x=x:5-x\Leftrightarrow (2-x)(5-x)=x^2 と辺の比からxの方程式がたち、これを解いて x=\frac{10}{7} が分かります。
実は、これでもうDのことを忘れることができます。代わりに、まだ図に書き込んでいなかったC~(AC=5)を加えます。
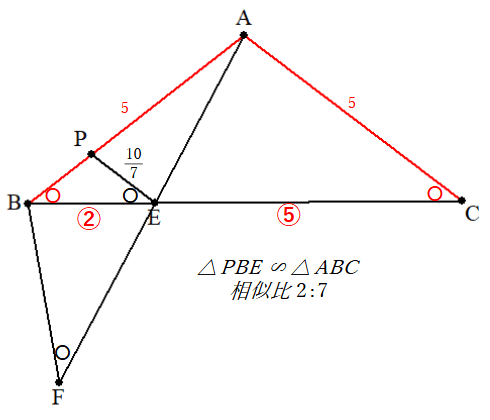
Cの追加により、AB=AC=5 で \triangle{ABC} も二等辺三角形であり、かつ \triangle{PBE} に相似だと分かります。
この相似比が PE:AC=\frac{10}{7}:5=2:7 なので、BE:EC=2:5 と長さの比が明らかになります。
これでPを忘れることができます。そして問題文で使っていない最後の条件 CF=10 を加えます。
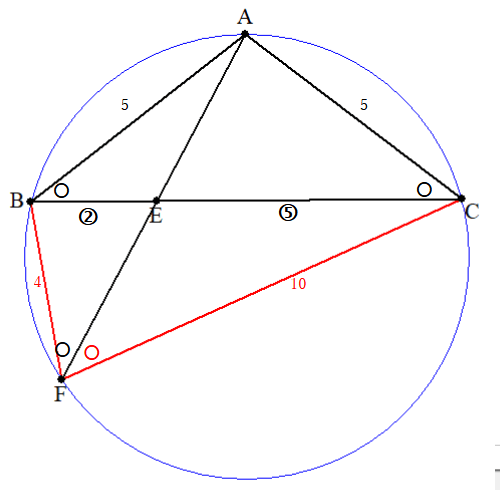
ただ、長さを考える前に、\angle ACB=\angle AFB から、これが同一の円弧に対する円周角になっておりA,B,F,Cが同一円周上にあること、そこから更に \angle ABC=\angle AFC と〇の角がもう一つ現れることを確認しておきます。
そうすると、直線FAが\angle Fの二等分線になっていますから、BF:CF=BE:CE=2:5 と辺の比が伝播し、BF=4 が分かります。
これでEも忘れることができ、最後に残るのは円に内接する辺の長さ5,5,4,10の四角形です。とてもすっきりした形になりました。
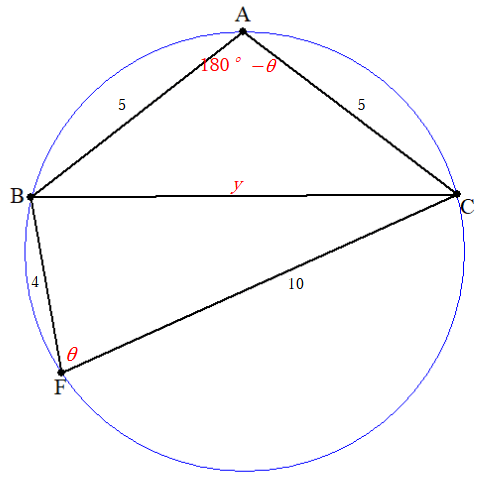
円に内接することから\angle F=\theta とおけば \angle A=180\degree-\theta です。BC=y とおいて余弦定理から条件式を整理します。
- 5^2+5^2-y^2-2\cdot 5\cdot 5\cos{(180\degree-\theta)}=0 \Leftrightarrow 50-y^2+50\cos{\theta}=0
- 4^2+10^2-y^2-2\cdot 4\cdot 10 \cos{\theta}=0 \Leftrightarrow 116-y^2-80\cos{\theta}=0
この2つの式の上の方の8倍と下の方の5倍を辺々足し合わせることで \cos{\theta} を消去し 8(50-y^2)+5(116-y^2)=0 これを解いて得られる \frac{14\sqrt{65}}{13} が答えとなります。
おわりに
ということで、比較的難易度が低めの前半、一気に半分を解説しました。
後半については、4問分と2問分に分けて解説していこうと思います。
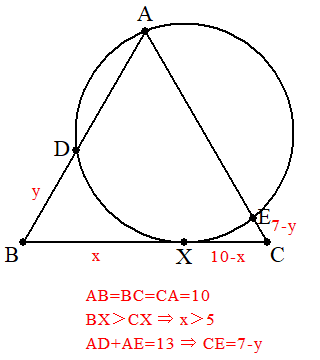
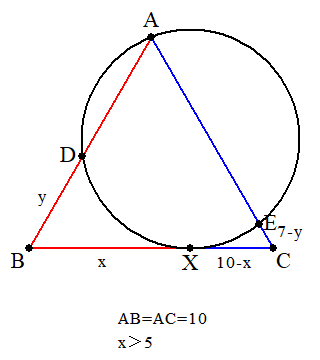
Discussion