🌈
ポアソン分布とガンマ分布の関係

2025/10/02に公開
 動機のための例：信頼区間の紹介単に母比率の信頼区間というとき，普通は二項分布モデルに基づく信頼区間を指す．二項分布に比べると見かける機会は少ないがポアソン分布でも比率を考えることがある．二項分布のパラメータは上限が 1 なので，上限が明確には決まっていないときはポアソン分布の方が使いやすい．
例えば，単位時間 T あたりのポンプの故障回数とか，単位面積 T あたり松の木の本数とかを扱うとき，それぞれ時間や面積との比 r をパラメータとしたいが上限が明確にはわからない．
このようなとき，故障回数や本数 X をパラメータ rT を持つポアソン分布 \mathrm{Pois}(r T) に従う確率変数としたモデルが考えられる．すなわち，

X \sim \mathrm{Pois}(r T).
このポアソン分布は比 r を明示的に含んでパラメータ化されている．T が時間や面積の単位 U を持つとすると r の単位は 1/U である．
r の信頼区間を考えるとき，次の関係を用いることができる．

\sum_{j \ge x} \frac{ (r T)^{j} \exp(-r T)}{j!}
= \frac{ T^x}{\Gamma(x+1)} \int_0^{r} u^x \exp(-u T)\, du.
\tag{1}
左辺を x の関数とみるとポアソン分布の補分布関数であり，右辺を r の関数とみるとガンマ分布の分布関数である．
次のように適当な数を選んで R で確認できる．
Ti = 10 #上ではT
r = 0.9
k = 11 #上ではx
> ppois(k-1, lambda = Ti*r, lower.tail = FALSE) #上側（補分布関数）
[1] 0.2940117
> pgamma(r, shape = k, rate = Ti, lower.tail = TRUE) # 下側（分布関数）
[1] 0.2940117
(1)より次の(2)も成り立つ．

\sum_{j \le x} \frac{ (r T)^{-j} \exp(-r T)}{j!}
= \frac{ \tau^{x-1}}{\Gamma(x)} \int_r^{\infty} u^{x-1} \exp(-u \tau) \, du
\tag{2}
Q(\alpha;a,b) をガンマ分布 \mathrm{Gamma}(a,b) の分布関数の逆関数としたら，(1)と(2)を用いて信頼区間 C(X) を次のように作ることができる．

C(X) = [Q(\alpha/2;X+1,T), \ Q(1-\alpha/2;X+1,T)] .
この信頼区間は R では poisson.test という関数で実装されている．
> res = poisson.test(x = k, T = tau, r = r, alternative = "two.sided")
> res$conf.int
[1] 0.549116 1.968204
attr(,"conf.level")
[1] 0.95
> c(qgamma(0.025, shape = k, rate = tau),
+   qgamma(0.975, shape = k+1, rate = tau))
[1] 0.549116 1.968204
加えて，ベイズ信頼区間も考えてみる．
r の事前分布としてガンマ分布 \mathrm{Gamma}(a,b) を用いると事後分布はガンマ分布 \mathrm{Gamma}(x+a,T+b) であり，ベイズ信頼区間 B(X) は次のように得られる．

B(X) = [Q(\alpha/2;X+a,T+b), \ Q(1-\alpha/2;X+a,T+b)] .
C(X) と B(X) を見比べると互いに似ていることがわかる．


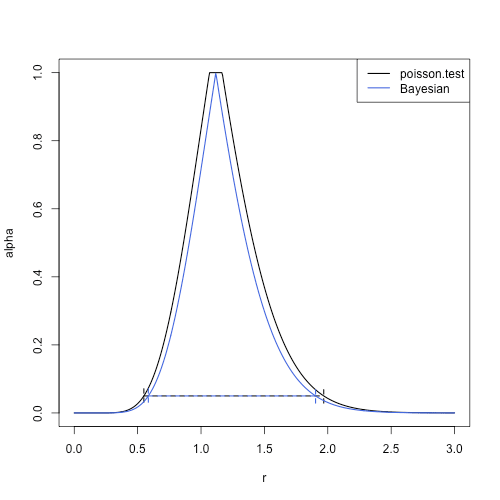
縦軸を \alpha ， 横軸を信頼区間とした関数（信頼区間関数 a.k.a. P値関数）．事前分布はジェフリーズの事前分布に相当する a=0.5, b=0 に設定した．
このように出発点の考え方が違っても似た結果が得られるというのは，数理的なことを学ぶ上でおもしろいポイントの一つだと思う．
以上により，（1）の関係を理解したい動機が得られたことにして，次節のシミュレーションに進む．

 数値計算してみる(1) は次のように捉えるとわかりやすい．

\begin{aligned}
P&(\text{ {\it t} 時間待ってイベントが {\it k} 回以上発生する})\\
&＝P(\text{イベントが {\it k} 回発生するまでの待ち時間が {\it t} 以下})
\end{aligned}
過去のイベント発生時刻に依存せず，一定の確率でイベントが起こるとし，イベントの生起間隔が連続型とするとこれは指数分布に従う．
次のようにシミュレーションを書くと「t 時間待ってイベントが k 回以上発生する」ことと「イベントが k 回発生するまでの待ち時間が t 以下」であることが同値だとわかる．
#イベントの回数を固定し待ち時間をシミュレーション
sim_waitingtime = function(iter, k){
  x = numeric(iter)
  for(it in seq_len(iter)){
    u = 0
    j = 1L
    while(j < k){
      ep = dqrng::dqrexp(1)
      u = u + ep
      j = j+1L
    }
    x[it] = u
  }
  return(x)
}

#待ち時間を固定しイベントの回数をシミュレーション
sim_count = function(iter, tau){
  x=integer(iter)
  for(it in seq_len(iter)){
    u=0
    j=0L
    while(u < tau){
      ep = dqrng::dqrexp(1)
      u = u + ep
      j = j+1L
    }
    x[it] = j-1L
  }
  return(x)
}
下の図で回数はポアソン分布，待ち時間はガンマ分布になることが確かめられる．


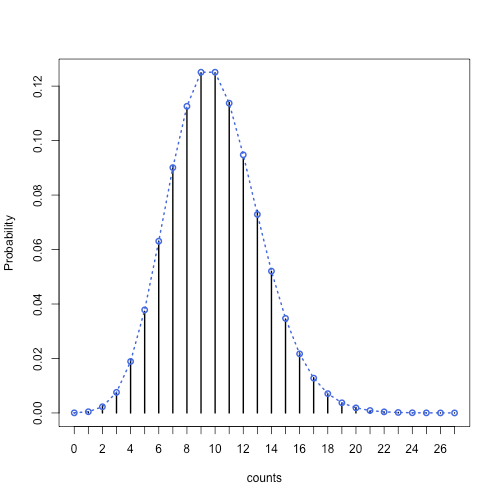
イベントの回数の分布．青いマーカーはポアソン分布の確率関数


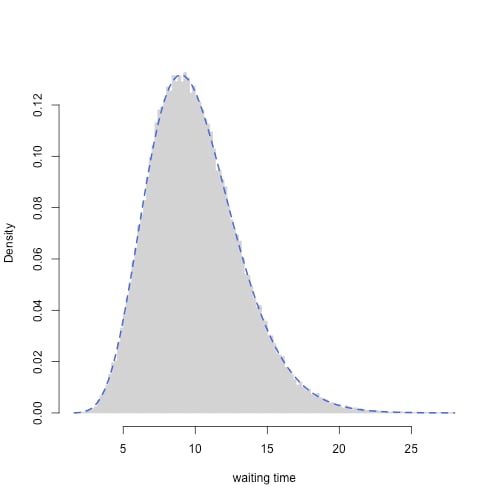
イベントの待ち時間の分布．青い点線はガンマ分布の密度関数

 手計算してみる(1) の左辺を G(r) とおく．

G(r) = \sum_{j \ge x} \frac{ (r T)^{j} \exp(-r T)}{j!}
微分して整理する．

\begin{aligned}
G'(r) &= \sum_{j \ge x} \frac{ jT }{j!} (r T)^{j-1} \exp(-r T) - \sum_{j \ge x} \frac{ T }{j!} (r T)^{j} \exp(-r T)\\
&= \sum_{j \ge x} \frac{ T }{(j-1)!} (r T)^{j-1} \exp(-r T) - \sum_{j \ge x} \frac{ T }{j!} (r T)^{j} \exp(-r T)\\
&= \frac{ T^x }{(x-1)!} r^{x-1} \exp(-r T) \\
&= \frac{ T^x }{\Gamma(x)} r^{x-1} \exp(-r T) 
\end{aligned}
G'(r) を積分すれば G(r) が得られる．

G(r) = \int^{r}_0 G'(r) \, dr =  \frac{ T^x }{\Gamma(x)} \int_0^r u^{x-1} \exp(-u T) \, du .
これで (1) がわかった．

 関連記事など指数分布が出てくるところはやや唐突に感じられるかもしれない．ベルヌーイ試行の待ち時間（幾何分布）の連続版として指数分布が出てくることを知ると納得感があるのではないかと思う．これについて，私家版・ポアソン分布の起源 で書いた．
より細かい話として，信頼区間の取り方は一通りではなく，今回の方針は片側P値の小さい方の2倍に対応する．これについては R の exact test についてのノート に書いた．
どの信頼区間を使うのがいいかは議論の余地があるが，こういう「微妙に数値が合わない」みたいな問題への対処としては，とりあえず分析に使ったコードを公開しておくのがいいと思う．
この投稿に使用したコードは以下におく：
https://github.com/abikoushi/Zenn_content/blob/main/R/rel_poisson_and_gamma.r
GitHubで編集を提案
動機のための例：信頼区間の紹介

数値計算してみる

手計算してみる

関連記事など

Discussion
