私家版・ポアソン分布の起源

はじめに

この投稿は 島谷健一郎『ポアソン分布・ポアソン回帰・ポアソン過程』（近代科学社） の1章「ポアソン分布の２つの起源」にヒントを得た内容です．

「確率 $p$ で成功するイベントの成功の回数の分布」という二項分布に比べるとポアソン分布はわかりにくいが，わかりにくいわりには基本的な分布の一つとして扱われる．

そこでシミュレーションを通じて理解を目指す．

動機付けのための例

あるソーシャルゲーム（ソシャゲ）ではユーザーが毎日同じ確率 $p$ でログインしているとする．

（なるべくイメージが持ちやすいようにこのような例にしてみたが，以降特別ソシャゲの話題が出てくるわけではないので，医学データに興味のある人はログインの代わりに症状の再発とか，品質管理に興味のある人は部品の故障とか，自分の興味のある題材に読み替えてもらえると嬉しい．）

ログインのあった日を $t_1, t_2, \ldots, t_x$ として，$N$ 日目まで観察するとしよう．

$N$ 日間のうち，$X=x$ 回ログインする確率は，次のように二項分布で表せる．

$$P(X=x) = \binom{n}{x} p^x (1-p)^{n-x}$$

そしてログインから次のログインまでの日数を $k_i = t_{i} - t_{i-1} - 1$ と置く. ログインから次のログインまでの待ち時間 $K=k_i$ は次の分布で表せる．

$$P(K=k_i) = p (1-p)^{k_i}$$

右辺は $k_i$ 回ログインしない日が続いてから1回（確率 $p$ で）ログインする確率である. これを幾何分布と呼ぶ．

さて，時間が日毎ではなく何時何分何秒とか，もう少し細かい単位で記録されている場面を考える．

結論を先取りすると，このときのログイン回数がポアソン分布に，ログインからログインまでの待ち時間が指数分布になることを次のシミュレーションで見ていく．

シミュレーション

次のようなルールでシミュレーションを行う．

1. 区間 $[0,1]$ の幅を n 等分して，それぞれの区画が独立に同じ確率 p で 1 （1-p で 0）の値を返す．
2. 1 が出た回数を記録
3. 1 が出た位置から次の 1 が出た位置までの間隔を記録
4. 2 と 3 を繰り返す

区画の数 n を増やすことが時間刻みの幅を小さくすることに相当する．

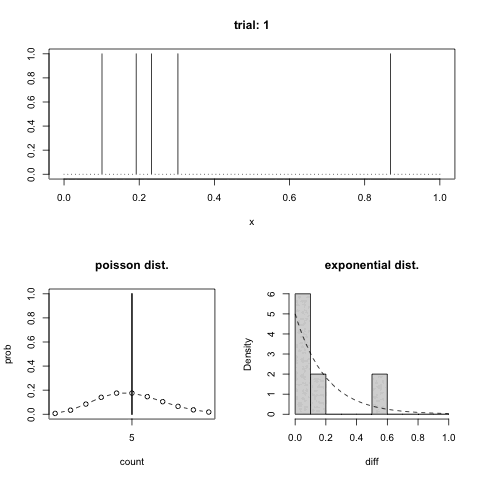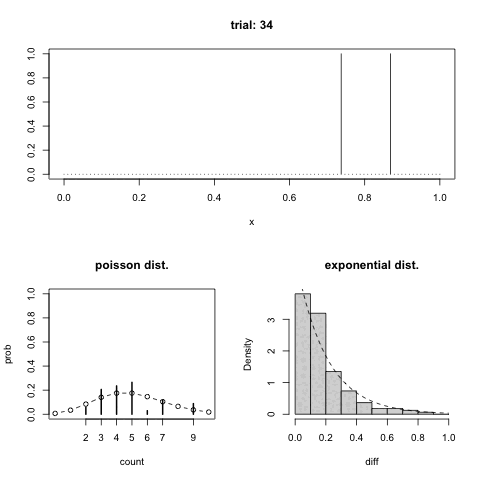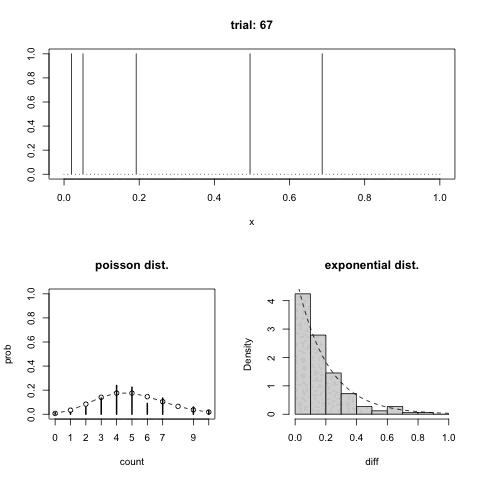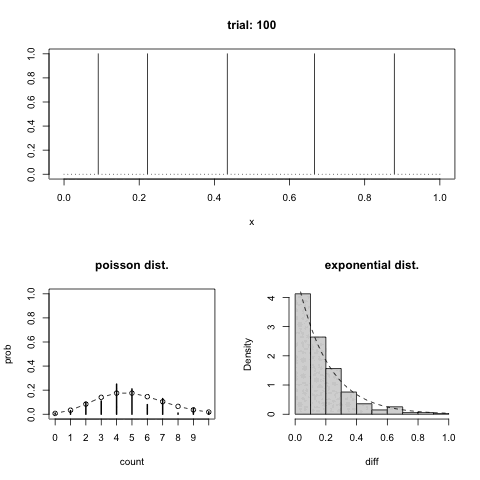
GIFアニメでは上のパネルが箇条書きの一番めの 1 の出た位置を示している．左下が箇条書きの二番めの分布，右下が三番めの分布を示している．曲線でポアソン分布と指数分布をそれぞれ重ねてある．

Rのコードはこちら：

https://github.com/abikoushi/Zenn_content/blob/main/R/sim_binom_to_poisson.R

発展的な話題のための補足

他の分布との関係

数理統計や確率論の教科書にはよく「二項分布のポアソン近似」や「二項分布の正規近似」についての定理が書かれている．例えば，野田一夫・宮岡悦良『入門・演習 数理統計』（共立出版）や藤田岳彦『弱点克服 大学生の確率・統計』（東京図書）に記載があることを確認した．

二項分布のポアソン近似についての定理はこんなふうだ：

「$\lambda=np$ が一定であるように $n \to \infty$，$p \to 0$ とするとパラメータ($n,p$)の二項分布がパラメータ $\lambda=np$ のポアソン分布になる」

一方，二項分布の正規近似についての定理はこんなふうだ：

「パラメータ($n,p$)の二項分布に従う確率変数 $X$ に対し，$Y=(X-np)/\sqrt{np(1-p)}$ とすると，$n \to \infty$ のとき $Y$ は標準正規分布に従う」

さて $np$ を固定して $n$ を大きくすることと，$p$ を固定して $n$ を大きくすることの区別がイメージできるだろうか．

できないとしても先のシミュレーションのコード rate = n*p が適当な数字になるように上のコードを動かしてみるとイメージが掴みやすくなるのではないか（もし本当にそうなったら嬉しい）．

統計モデルについて

例で述べた「毎日同じ確率でログインする」というのは自然な仮定ではない．

しかし，適切な統計モデルの選択というのはほとんどいつも難しく，より複雑な（自由パラメータの多い）モデルや，より単純な（自由パラメータの少ない）モデルと比べてみることがベスト・プラクティスになることが多い．そのときに，「時間に対し一定」のような単純なモデルからはじめておくと，うまくいかなかったときにどの部分がよくなかったのかがわかりやすい．

また，モデルが現実のデータを十分に近似してるとは言えないとしても，「時間に対し一定」のように平にならしてみたらおなじ物差しでユーザーAとユーザーBを比べることはできる．

統計モデルの場合，「基本的」というのはこの程度の意味であることが多いように思う．「自然界の基本的な法則」とかいうときのように，「〇〇則に従って現実の母集団がポアソン分布に従う」ということにはなかなかならない．