帰納/余帰納を理解するための単語の整理（圏論）

背景：圏そのものについて初歩的な事をきちんと理解していなかったので、理解するための単語の整理をする。
1/25: この記事の簡単な結論と、次の記事につながる話を追記
この記事の続き：始代数による帰納的計算に親しむ - なぜ自然数は0を含むか（圏論）

以下、$\mathcal{C}$は適当な圏を表すものとし、$\mathcal{F}: \mathcal{C}\to \mathcal{C}$は適当な自己関手とする。
$\bold{Obj}(\mathcal{C})$で$\mathcal{C}$の対象を表す。
$X,Y \in \bold{Obj}(\mathcal{C})$のとき、$\hom_{\mathcal{C}}(X,Y)$で$X$から$Y$への射全体の集合を表す。誤解のおそれの無い場合は、単に$\hom(X,Y)$と書く。

始対象、終対象

定義（始対象、終対象）

圏$\mathcal{C}$の始対象$X$とは、$X \in \bold{Obj}(\mathcal{C})$であって以下の条件を満たす対象のこと。

$$\forall Y \in \bold{Obj}(\mathcal{C}), |\hom(X,Y)| = 1.$$

つまり、任意の対象$Y$について、$X$から$Y$への射が一つしか存在しないとき、$X$を始対象とよぶ。

この双対を定義できる。つまり、$X$が次の条件を満たすとき、$X$は終対象である：

$$\forall Y \in \bold{Obj}(\mathcal{C}), |\hom(Y,X)| = 1.$$

例（始対象、終対象）

集合の圏$\bold{Set}$において、任意の一要素からなる集合を考えた時、その集合への射はすべての要素を単一の要素に移す写像となり、つまり射は一つしかない。したがって、任意の一要素からなる集合は終対象である。また、空集合から任意の集合に対して、空写像を射と思うことにすると、空集合は始対象となる。

群の圏$\bold{Grp}$において、単位元のみからなる群は始対象かつ終対象である。群の射の場合は、単位元を単位元に移さなければならないので、いずれの場合も射の数は一つに限られるからである。

その他の例は、この記事の末尾を参照。

始対象が2つ（以上）存在したとき、それらは同型である。実際、$A$が始対象であるとき、$A$から$A$自身への射は$\mathrm{id}_A$しかないが、一方で始対象$A$と別の始対象$B$との間には必ず双方向の射が存在するので、それを合成することで$\mathrm{id}_A, \mathrm{id}_B$が得られ、同型となる。

定義（零対象）

$X\in \bold{Obj}(\mathcal{C})$が始対象かつ終対象のとき、$X$を零対象という。

（直）積、余積

地味にこの記事を書こうと思った主因。というのは、$1+A\times A^*$という表記を見かけたときに、和って対象の圏の説明なしに簡単に使えるものなんだっけ、というのが言葉の整理を始めた理由だった。

定義（積）

$X, Y\in \bold{Obj}(\mathcal{C})$に対して、もし次の性質を満たす対象$Z \in \bold{Obj}(\mathcal{C})$および$\pi_X: Z\to X, \pi_Y: Z\to Y$が存在するときには、この３つ組$(Z, \pi_X, \pi_Y)$を積と呼び、$Z=X\times Y$と書く。また、$\pi_X, \pi_Y$を標準射影と呼ぶ。

性質：任意の$A \in \bold{Obj}(\mathcal{C}), f_X: A \to X, f_Y: A \to Y$に対して、ある$f: A \to X\times Y$がただひとつ存在して、次の図式が可換になる。

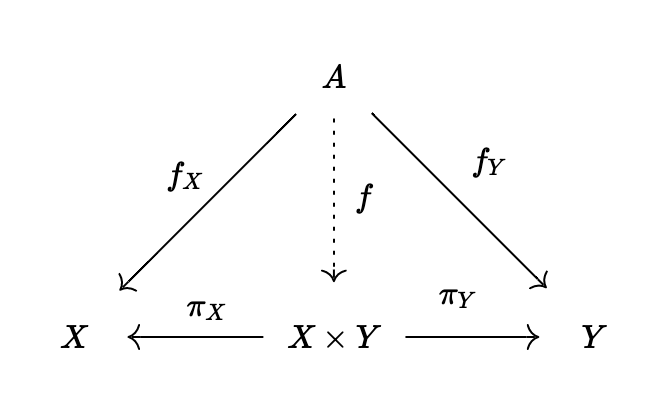
主張（積）

上記の定義はwell-definedである。つまり、$X\times Y$は存在すれば同型を除いて一意に定まる。

実際、$W, Z$が共に上記の普遍写像性質を満たすとすれば、$W$に関する射影$\pi_{WX}, \pi_{WY}$および$Z$に関する標準射影$\pi_{ZX}, \pi_{ZY}$に関して上記の可換図式を書くことで$W$と$Z$の間の同型射を構成できる。

一般に、$I$を適当な添字集合とするとき、$\prod_{i\in I} X_i$を同様の可換図式によって定めることができる。

例（積）

集合の圏$\bold{Set}$において、圏としての積はふつうのデカルト積（直積）になり、標準射影はデカルト積に対する射影になる。
ほか、いくつかの初歩的な例においては積が直積と一致する（例えば、群の圏などでもそうなる）が、一般には必ずしも対象を集合と見た時のデカルト積と一致するわけではない。（重要）

定義（余積、和）

積の双対を余積という。つまり、３つ組$(Z, \iota_X, \iota_Y)$が次の性質を満たす時に余積または和と呼び、$Z=X+Y$と書く。また、$\iota_X, \iota_Y$を標準入射と呼ぶ。

性質：任意の$A \in \bold{Obj}(\mathcal{C}), f_X: X \to A, f_Y: Y \to A$に対して、ある$f: X+Y \to A$がただひとつ存在して、次の図式が可換になる。

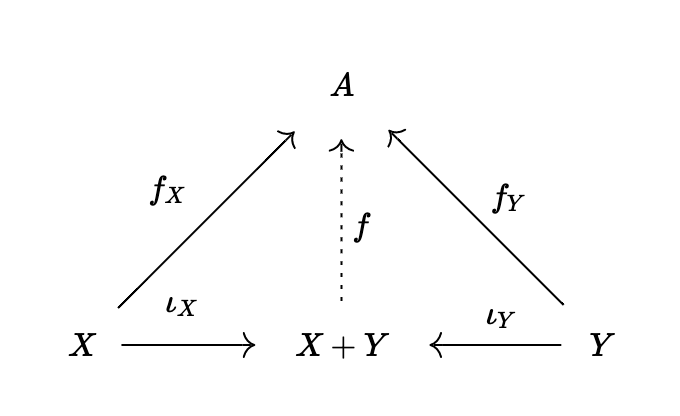
余積も同型を除いて一意に定まる。

例（余積）

集合の圏$\bold{Set}$において、圏としての和は集合としてのdisjoint unionになる。これのために、「余積も積と同様に集合の直和で考えればいいのかな」という邪念を生じがちである。
適当な環$A$上の加群の圏$A\bold{Mod}$において、圏としての和は加群としての直和である。これのために少し混乱しがちだが、例えば$A=\mathbb{Z}$とするとき、適当な可換群の（有限な）直和$X\oplus Y$というのは集合としてはデカルト積$X \times Y$と同型なので、集合の圏における$X+_{\bold{Set}}Y$とは意味が異なっている。（そのため、圏を指定しなくて$+$の意味ってあるんだっけ...？となったので、この記事を書いた。）
群の圏$\bold{Grp}$において、圏としての和は自由積である。これは重要な事実であり、例えば$X,Y\in \bold{Grp}$を適当な無限巡回群($X=\{x^n|n\in \mathbb{Z}\}, Y=\{y^n|n\in \mathbb{Z}\}$)とするとき、群の圏における和$X+Y$は自由加群の直和にはならないということである。同時に、集合の圏の直和（disjoint union）とも異なっている。このように、考える圏によって同じ$+$でも異なる意味を持つというのは面白い。

$\mathcal{F}$-代数

ここでいう代数は、適当な体上のベクトル空間に積の構造が入ったもののことではなく、群なども含めて抽象化した対象として呼ぶ時の意味での代数のことである。$\mathcal{F}:\mathcal{C}\to\mathcal{C}$は自己関手。

定義（$\mathcal{F}$-代数）

$A\in \bold{Obj}(\mathcal{C}), \alpha \in \hom(\mathcal{F}(A), A)$のとき、2つ組$(A, \alpha)$は$\mathcal{F}$-代数であるという。

定義（$\mathcal{F}$-代数準同型）

$(A, \alpha), (B, \beta)$を$\mathcal{F}$-代数とする。$f:A\to B$が$\mathcal{F}$-代数準同型であるとは、$f \circ \alpha = \beta \circ \mathcal{F}(f)$を満たすことをいう。つまり、次の図が可換であることを意味する。

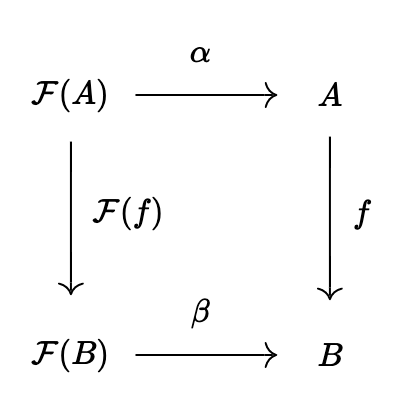
定義（$\mathcal{F}$-代数の圏）

$\mathcal{F}$-代数の全体を対象として、$\mathcal{F}$-代数準同型を射とすることにより、圏が構成される。

実際、$(A,\alpha)$が$\mathcal{F}$-代数のとき、定義式で$A=B$をとると$\mathrm{id}_A$が$\mathcal{F}$-代数準同型になる事はあきらかで、射の合成可能性については上記可換図式をつなげて書くことで簡単に示される。

定義（$\mathcal{F}$-始代数）

$(A,\alpha)$が$\mathcal{F}$-代数であり、かつ$\mathcal{F}$-代数の圏の中で始対象になっているとき、$(A,\alpha)$を$\mathcal{F}$-始代数と呼ぶ。

例（$\mathcal{F}$-代数）

集合の圏$\bold{Set}$において、1要素からなる適当な集合を$1$と書くことにする。（$1$は終対象である。）
自己関手$\mathcal{F}:\bold{Set}\to \bold{Set}$を$X\mapsto 1+X = 1 +_{\bold{Set}} X$で定める。ただし、$\mathcal{F}$は射を自然な埋め込みによって移す。
また、$\mathrm{zero}:1 \to \mathbb{N}$を、$\mathrm{zero}(x) = 0 (x\in 1)$によって定め、$\mathrm{succ}:\mathbb{N} \to \mathbb{N}, n \mapsto n+1$とする。
このとき、$(\mathbb{N}, [\mathrm{zero}, \mathrm{succ}])$は$\mathcal{F}$-代数になる。（これは半ば自明である）

また、$(\mathbb{N}, [\mathrm{zero}, \mathrm{succ}])$は$\mathcal{F}$-始代数にもなっている。
実際、次の図に従って代入して計算をしてみよう。

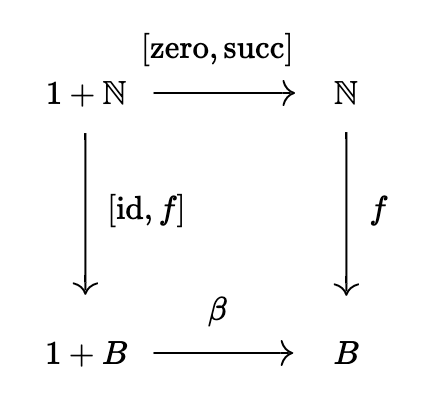
$1$の唯一の要素を$\mathrm{one}$とすると、$\mathrm{one}$について上の経路から

$$f \circ [\mathrm{zero}, \mathrm{succ}](\mathrm{one}) = f(0)$$

これが左の経路と等しいので、

$$f(0) = \beta \circ [\mathrm{id}, f] (\mathrm{one}) = \beta(\mathrm{one})$$

同様に、$0$について計算をすると、

$$f \circ [\mathrm{zero}, \mathrm{succ}](0) = f(1)$$

これが左の経路と等しいので、

$$f(1) = \beta \circ [\mathrm{id}, f](0) = \beta(f(0)) = \beta(\beta(\mathrm{one}))$$

以下、同様に

$$f(1) = \beta\circ\beta(\mathrm{one})$$

$$f(2) = \beta\circ\beta\circ\beta(\mathrm{one})$$

...
ということを示せるので、$f$の値が$\beta$によって定義されてしまうことがわかる。逆に、このようにして定めた$f$は任意の$1+\mathbb{N}$の要素について上記の可換図式を満たすことになり、$\beta$に対して$f$が一意に定まることがわかる。従って$(\mathbb{N}, [\mathrm{zero}, \mathrm{succ}])$は$\mathcal{F}$-始代数である。□

一般論として、適当な$\mathcal{F}$に対して$\mathcal{F}$-始代数を与えることができれば、射の一意性によって$\mathcal{F}$-代数$(B, \beta)$から$f$が定まることがわかる。このような点において、帰納的定義と始代数は相性がよい。

任意の$\beta$に対して$f$をただひとつ決めるような計算は、高階関数の計算においてしばしば出現する。そのような計算での例を続きの記事で述べる。
また、双対であるところの終余代数がどのように活用できるのか、という事についても続きの記事で述べる。

補題（$\mathcal{F}$-始代数）

• $\mathcal{F}$-始代数は同型を除いて一意。
• $(A, \alpha)$が$\mathcal{F}$-始代数のとき、$\mathcal{F}(A)$と$A$は同型。□

これらの議論の双対を考えることで、$\mathcal{F}$-余代数、$\mathcal{F}$-終余代数を考えることができる。

補遺

この記事の続き：始代数による帰納的計算に親しむ - なぜ自然数は0を含むか（圏論）

始対象と終対象のその他の例はWikipedia等に詳しい：始対象と終対象
※主張の正誤を判断できない場合は、さらにWikipediaで参考文献として挙げられたものを参照のこと。

積の例：積 (圏論)
余積の例：余積
$\mathcal{F}$-代数の例：F代数

※wikipedia、昔と比べると随分詳しくなりましたね。