始代数による帰納的計算に親しむ - なぜ自然数は0を含むか（圏論）

帰納/余帰納を理解するための単語の整理（圏論）の続き。
積や和、代数、始代数などの定義は上記記事を参照のこと。

ちなみに、この記事を読むと「なぜ自然数は$0$から始まると考えるべきか」という事がわかる。

以下、$\mathcal{C}$は適当な圏を表すものとし、$\mathcal{F}: \mathcal{C}\to \mathcal{C}$は適当な自己関手とする。
$\bold{Obj}(\mathcal{C})$で$\mathcal{C}$の対象を表す。
$X,Y \in \bold{Obj}(\mathcal{C})$のとき、$\hom_{\mathcal{C}}(X,Y)$で$X$から$Y$への射全体の集合を表す。誤解のおそれの無い場合は、単に$\hom(X,Y)$と書く。
自然数$\mathbb{N}$は$0$を含む。
適当な集合$A$に対して、$A^0$は単一の要素 $\epsilon$ : ∅→$A$ からなる集合とする。
※$A^n$は、$A^{\{0,1,\cdots, n-1\}}$、つまり$\{0,1,\cdots, n-1\}$から$A$への写像全体のなす集合と同一視できるため、$A^0$も要素が0個の集合（＝空集合）からの写像の集合と思ってよい。

$\mathcal{F}$-代数

例（リストを$\mathcal{F}$-代数と思う方法）

集合の圏$\bold{Set}$において、$A\in \bold{Obj}(\bold{Set})$を適当な集合とする。
このとき、$A^* = \coprod_{n \in \mathbb{N}}A^n$とすると、この$A^*$は【$A$の要素からなる任意の有限長のリスト】の集合に対応している。
※注意：$a\in A^*$であるとき、あくまでも適当な$n$に対して$a\in A^n$であるため、$a$の長さは有限であることに注意する。

さて、$1$で1要素からなる集合を表すことにする。
関手$\mathcal{F}$を$\mathcal{F}(X) = 1+A\times X, \mathcal{F}(f) = [\mathrm{id}_1,\mathrm{id}_A \times f]$によって定める（ことができる）。

主張（リストは$1+A\times X$-始代数）

$\alpha:\mathcal{F}(A)=1+A\times A^* \to A^*$を、以下の要領で定める。

$\mathrm{one} \in 1$について、$\alpha(\mathrm{one}) = \epsilon$。
$a\in A, a^* \in A^*$について、$\alpha(a\times a^*) = a\times a^*$。（$a\times a^* \in A^*$であることに注意する。また、$a\times \epsilon = a$と思う。）

主張：このとき、$(A^*, \alpha)$は$\mathcal{F}$-始代数である。

証明の概要（リストは$1+A\times X$-始代数）

これも、ある$\mathcal{F}$-代数$(B, \beta)$と、$(B, \beta)$への$(A^*, \alpha)$からの射$f$が与えられた時、$f$が$\beta$によって一意に定まることを確認しよう。

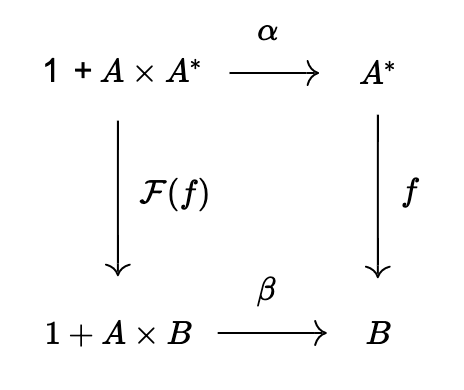
$\mathrm{one}$について上の経路から

$$f \circ \alpha(\mathrm{one}) = f(\epsilon)$$

これが左の経路と等しいので、

$$f(\epsilon) = \beta \circ [\mathrm{id}_1, \mathrm{id}_A\times f] (\mathrm{one}) = \beta(\mathrm{one})$$

同様に、$a\times \epsilon \in A\times A^*$について計算をすると、

$$f \circ \alpha(a\times\epsilon) = f(a)$$

これが左の経路と等しいので、

$$f(a) = \beta \circ [\mathrm{id}_1, \mathrm{id}_A\times f](a\times \epsilon) = \beta(a\times f(\epsilon)) = \beta(a\times \beta(\mathrm{one}))$$

以下、同様に

$$f(a\times a') = \beta(a\times f(a')) =\beta(a\times \beta(a'\times \beta(\mathrm{one})))$$

というように、$f(\epsilon), f(a), f(a\times a'), \cdots$というように$A^*$の次数（どの$A^n$に属するか）によって帰納的に計算ができる。そうすると、$f$が任意の$a_1\times\cdots a_n \in A^n$に対して計算され、$f$が一意的に定まることになり、$(A^*, \alpha)$が始代数であることがわかった。□

整合性の確認

実は、$A=1$（1要素からなる集合）とするとき、$1+1\times X \simeq 1+X$なので、これの始代数は前回の記事でみた自然数そのものなのであった。つまり、自然数とは、1つの値しか取らない型のリストと同型という事である。
当たり前ではあるが、中々面白い事実であり、確かに整合的な話になっている。
また、このような見方をするとき、$A=1$とした$\mathbb{N}$においては$\mathbb{N}$の始まりが$0$であろうと$1$であろうと問題がなかったが、$A$として任意の集合を取るときには、$1+A\times X$において考察をする上では$\mathbb{N}$は$0$から始まるべきである、という事を示している。

実際、$|A|\neq 1$として、もし$A^*$のかわりに$\epsilon$を含まない$A'=\coprod_{n\geq 1}A^n$をとると、$1+A\times A'$から$A'$への性質の良い全射を構成できないため、適当な代数$(B, \beta)$に対して$f(a) a\in A$が一意に定まらない。
いま、$\alpha$における$1$の移先が$\epsilon$、いわゆる空リストに対応する要素であった事を思い出すと、空のリストの存在を認める限りでは、自然数としても0（集合論、フォン・ノイマンの構成的には空集合）を認めるべきであるということと対応している事になる。つまり、空リストを実用上認める立場で物事を考える限りでは、自然数にも0を含むと解釈したほうが"自然"である、という事を示している。
ここで詳しくは述べないが、$1+A\times X$という関手の構成においては$1$と$A\times X$という２つの"コンストラクタ"が用いられていると考えることができ、それぞれがnil: () -> Listとcons: A -> Listに対応していると考えることができる。

ちなみに、空リストを認めない立場では、$A+A\times X$という関手を考える事ができる。（$A=1$のときは、自然数が1から始まってもよい事実と対応している。）
この場合には、$A'=\coprod_{n\geq 1}A^n$をとり、類似の射を与えることで始代数になる。

例（$A+X$）

ここまで、$1+X$と$1+A\times X$について見たが、$X$の"係数"ではなくて"定数項"を変化させるとどうなるだろうか。
たとえば、$n$個の要素からなる集合を単に$n$と書き、$n+X$について調べよう。

主張（$n+X$の始代数は$n\times \mathbb{N}$）

$n+X$に対して、代数$(n\times \mathbb{N} = \mathbb{N}_0 + \cdots + \mathbb{N}_{n-1}, \alpha)$を$\alpha(i) = 0_i \in \mathbb{N}_i, \alpha(m_i) = (m+1)_i \in \mathbb{N}_i$で定める。
このとき、$(n\times \mathbb{N}, \alpha)$は$n+X$始代数となる。

これまでの議論と同様に、$i\in n$および$m_i \in \mathbb{N}_i$の移る先を調べればわかる。□

いま、わかりやすさのために$n$を取ったが、実際には任意の$A$で同様の議論が成立する。
これは、$1+A\times X$と時と対照的で、$\mathbb{N}$の数が増えるというような結果になるのである。

例（二分木：$A+X\times X$）

ここで、$X$の"次数"が上がった場合には、どのような事が起こるだろうか。$A+X\times X$というものを考えてみよう。

実は、適当な集合$A$を与えた時、$A$の値を取るような"nilを許さない"ツリー、二分木を表現する関手が、$A+X\times X$によって構成できる。つまり、$A$が末端の葉の値を表していて、$X\times X$が左の枝と右の枝を表している。
これは、射$f:X\to Y$が与えられた時に$\mathrm{id}_1+f\times f$に移すことによって関手を定める。この関手についての始代数が、$A$の中の適当な要素が節点の値であるような木の集合$T(A)$と一致する。
つまり、$\alpha: A+T(A)\times T(A) \to T(A)$を、$\alpha(a) = a\in T(A), \alpha(t_1\times t_2)$を$t_1$と$t_2$の"上"に根となる節点を付け加えてできる木（葉以外は値を持たない！）とすると、この$\alpha$は全単射＝一対一対応になっているが、さらには...

主張：$(T(A), \alpha)$は$A+X\times X$-始代数である。

証明の概要（$(T(A), \alpha)$は$A+X\times X$-始代数）

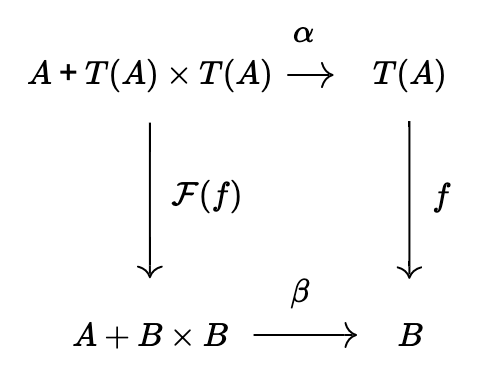
$a\in A$について上の経路から

$$f \circ \alpha(a) = f(a)$$

これが左の経路と等しいので、

$$f(a) = \beta \circ [\mathrm{id}_A, f\times f] (a) = \beta(a)$$

ここで、$a\times a' \in T(A)\times T(A)$とすると、

$$f \circ \alpha(a\times a') = f(<a,a'>)$$

これが左の経路と等しいので、

$$f(<a,a'>) = \beta \circ [\mathrm{id}_A, f\times f](a\times a') = \beta(f(a)\times f(a')) = \beta(\beta(a)\times \beta(a'))$$

以下、同様にして$(T(A), \alpha)$が始代数であることが示される。

$A+X$と$A+X\times X$の類似性について

$A+X$については、$A\times \mathbb{N}$が始代数となるのだったが、ここで$\mathbb{N}$が要素数1の型のリストと同一視できたことを思い出すと、実は$A\times \mathbb{N}$は"末尾（あるいは先頭）のみ$A$の値をとるリスト"と思うこともできる。
そのような観点で考えると、$A+X$と$A+X\times X$にはある種の類似性があり、統一的な考え方で説明できることがわかる。
逆に、この二分木は、末端の葉でしか$A$の値を持たないため、$1+A\times X$とは類似性がない。この事を次で考察する。

例（節点も値を持つ二分木：$1+A\times X\times X$）

先程の例では、節点は値を持たず、末端の葉に限り$A$の値を持つことができた。しかし実際には、節点に値を持つような木も使われる。
そのような木は、リストの場合と同様に、空木（深さ＝高さが0の木）も含めて$1+A\times X\times X$という式で考えることができる。

主張：$\mathcal{T}(A)$によって節点でも$A$の値を取るような木の集合とするとき、$(\mathcal{T}(A), \alpha)$が始代数になる。ただし、$\alpha$は、$1$の要素を空木に、$a\times l\times r$を根の値が$a$、左（１つ目）の枝が$l$、右（2つ目）の枝が$r$になるような木$(a,l,r)$に移す写像とする。ただし、$\epsilon$を高さ0の木とするとき、$(a,l,\epsilon)$は$a$の左に$l$、右には枝を持たない木であり、$(a,\epsilon,r)$は$a$の右に$r$、左には枝を持たない木である。

証明の概要（$(\mathcal{T}(A), \alpha)$は$1+A\times X\times X$-始代数）

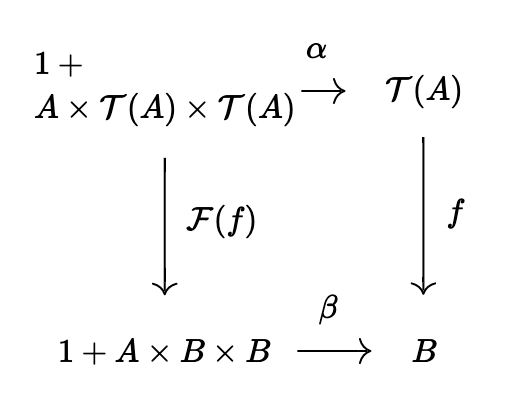
これまでと同様の議論を、$l,r$の節点の数について順番に行えばよい。

例（$1+A\times X\times X\times X$）

これまでは、一つの節点がたかだか2つの枝を持つ場合を扱ったが、一般の木にはいくつ枝があってもよい。
枝を3つに増やした場合を考えることもできる。
もはや詳しくは書かないが、同様の事が成り立つ。

補遺

この記事では、具体的な始代数に関する計算を通して、帰納的計算に親しんだ。
このようなデータ構造たちのことを、代数的データ型という。この代数という語は、$\mathcal{F}$-代数に由来している。
なお、そもそもの話として、なぜ$\mathcal{F}$-代数という言葉があの定義に対して使われているのか？という事が疑問に思われるかもしれない。これは、群や環などの、いわゆる代数的な数学的対象について、この$\mathcal{F}-$代数と普遍性によってその構造を定義できるという事に由来している。（しかし、ここでは詳しく説明しない）

ところで、この記事で扱ったデータ構造は、すべて集合の要素としては有限になっている。
つまり、対象としての$A^*$や$T(A)$などは無限集合であっても、その中身である一つ一つのリストや木を見たときには有限の長さ・深さしかなかった。
ところが、この始代数の圏論的双対、終余代数を取る時、じつは無限集合を相手とした計算が行えるのであった。
一般に人間が計算や考察を行う際に、ある対象の要素・満たす性質のすべてを取り出してから構成的に考察を行うのではなくて、一部の性質を取り出して考察を行い、そのような性質を満たす対象がどのようなものかを考えてから、個別の対象がそれを満たすことを示すという事がしばしば行われる。
このような、ある意味で演繹的な考え方や証明と相性のよい「余帰納」について、つづきの記事で述べる。

※数学的帰納法も演繹的な議論ではあるが