ロジカル思考を深める：演繹法と帰納法を駆使したアルゴリズム解説

1. はじめに

ロジカル思考（論理的思考）は、物事を整理し、合理的な結論を導くための重要なスキルです。
プログラミングやアルゴリズム設計においても、ロジカル思考を活用することで、より効率的で堅牢なコードを書くことができます。

本記事では、代表的なロジカル思考である 演繹法（Deduction） と 帰納法（Induction） に焦点を当て、それぞれの特徴や具体例、アルゴリズムへの応用について詳しく解説します。

ロジカル思考とアルゴリズム思考がどのように連携し、より効率的な問題解決へと導くのか、その融合の秘訣について詳しく知りたい方は、こちらの記事【ロジカル思考とアルゴリズム学習：効率的な問題解決の第一歩】をご覧ください。

---

2. 演繹法（Deduction）

2-1. 演繹法とは？

演繹法とは、一般的なルールや原則から論理的に結論を導く思考法 です。
数学の証明やプログラムの設計において、厳密なルールのもとで論理を積み上げていく場面でよく使われます。

例:

1. 前提1: すべての偶数は 2 で割り切れる
2. 前提2: 8 は偶数である
3. 結論: したがって、8 は 2 で割り切れる

このように、すでに確立された事実を組み合わせて、新たな結論を論理的に導き出します。

---

2-2. アルゴリズムへの応用

演繹法は、アルゴリズムの設計や検証 において重要な役割を果たします。
特に、以下のような分野で活用されています。

(1) 並べ替えのアルゴリズム

並べ替えのアルゴリズムは、既存のルールに基づいてデータを整理する手法の典型です。
たとえば、クイックソート（QuickSort） は次のような演繹的な手順を取ります。

python

def quicksort(arr):
    print(f"Current array: {arr}")  # 現在の配列を表示

    if len(arr) <= 1:
        return arr  # ベースケース（最小の問題に分解）

    pivot = arr[len(arr) // 2]  # 配列の中央の要素をピボットにする
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]

    # 変遷（データ分割）を表示
    print(f"Pivot: {pivot}")
    print(f"Left: {left}, Middle: {middle}, Right: {right}")

    return quicksort(left) + middle + quicksort(right)  # 再帰処理として適用

# テストデータ
test_data = [3, 6, 8, 10, 1, 2, 1]
print(f"Original array: {test_data}")
sorted_data = quicksort(test_data)
print(f"Sorted array: {sorted_data}")

• 並べ替えのアルゴリズムとして、クイックソートは再帰処理を用いた技術的なアプローチを取っています。
• その一方で、演繹的な思考法を使って、問題を「分割して解決する」という一般的な原則から具体的な手順を導いているため、思考法としては演繹的と言えます。

このように、再帰処理と演繹法は異なる概念ですが、クイックソートはその両方を含んでいます。

演繹的なポイント:

• 配列を 「pivot より小さい部分」「pivot」「pivot より大きい部分」 に分割するというルールを適用
• 分割統治法（Divide and Conquer)により、部分問題を再帰的に処理

このように、一般的な原則（分割統治法）を個々のケースに適用することで、論理的に正しいアルゴリズムを構築できます。

(2) 論理プログラムと自動推論

演繹法は、Prolog などの論理プログラミングにも使われます。

prolog

parent(john, mary).
parent(mary, alice).

ancestor(X, Y) :- parent(X, Y).
ancestor(X, Y) :- parent(X, Z), ancestor(Z, Y).

このプログラムでは、

• 「ある人物 X が Y の祖先である」という結論を、親子関係のルールを適用して導くことができます。

論理ルールを積み上げて結論を導く点で、演繹法が活用されています。

アルゴリズムの基礎について詳しく学びたい方はこちらの記事を参考にしてください。
【アルゴリズムとは？】

---

3. 帰納法（Induction）

3-1. 帰納法とは？

帰納法とは、具体的な事例やデータから一般的なルールを導き出す思考法です。
データ分析や機械学習の分野では、帰納法によってパターンを見つけ出し、新たな知見を得ることができます。

例:

1. 観察1: 昨日の夕方、カラスは黒かった
2. 観察2: 今日の朝、カラスは黒かった
3. 観察3: 今日の昼、カラスは黒かった
4. 結論: したがって、「カラスは黒い」という法則があるかもしれない

このように、複数の観察から一般法則を推測するのが帰納法の特徴です。

---

3-2. アルゴリズムへの応用

帰納法は、主に「データからルールを学習する」アルゴリズムに応用されています。

(1) 機械学習（Machine Learning）

機械学習は、データを分析し、規則性を見つけることにより予測モデルを作成します。
例えば、以下のような線形回帰のモデルは、帰納法的な手法を用います。

python

from sklearn.linear_model import LinearRegression
import numpy as np

# データセット（x: 広告費, y: 売上）
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2, 4, 6, 8, 10])

# 回帰モデルの作成
model = LinearRegression()
model.fit(X, y)

# 新しいデータの予測
print(model.predict(np.array([[6]])))  # 出力: [12.]

帰納的なポイント:

• 過去のデータ（広告費と売上）から法則を導く
• 得られた法則をもとに、新しいデータ（広告費 6）の売上を予測

機械学習全般は、データをもとに一般ルールを見出す帰納的思考の典型例です。

---

(2) 経験則のアルゴリズム

別名ヒューリスティック（Heuristic）とは、「完全な正解がわからない中で、経験則に基づいて良い解を導く方法」です。
例えば、迷路を解く際に「右手法（常に右の壁に沿って進む）」を使うのは、過去の経験に基づいた帰納的な戦略です。

python

# 迷路の定義（0: 通路, 1: 壁）
maze = [
    [1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 0, 1, 0, 1],
    [1, 0, 1, 0, 1, 0, 1],
    [1, 0, 1, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1]
]

# 方向の定義（文字列で管理）
directions = {
    "右": (0, 1),
    "前": (1, 0),
    "左": (0, -1),
    "後": (-1, 0)
}
direction_order = ["右", "前", "左", "後"]  # 方向の順番をリストで管理

def right_hand_rule(maze, start, goal):
    x, y = start
    direction = "右"  # 初期方向

    def can_move(dir_name):
        dx, dy = directions[dir_name]
        return maze[x + dx][y + dy] == 0  # 進めるなら True

    while (x, y) != goal:  # ゴールに着くまでループ
        # 右 → 前 → 左 → 後 の順に進めるかチェック
        for i in [1, 0, -1, 2]:  # 右→前→左→後
            new_index = (direction_order.index(direction) + i) % 4
            new_dir = direction_order[new_index]

            if can_move(new_dir):
                direction = new_dir
                dx, dy = directions[direction]
                x += dx
                y += dy
                break  # 進んだら次のループへ
    return (x, y)

# スタート (1,1) → ゴール (3,5)
start = (1, 1)
goal = (3, 5)

result = right_hand_rule(maze, start, goal)
print("ゴール到達:", result)  # (3,5) に到達すれば成功

このような経験則ベースの探索手法も、帰納法の一種といえます。

演繹法や帰納法がアルゴリズムにどのように活用されるかを見てきましたが、もしアルゴリズムの基礎から詳しく学びたい方は、こちらの記事【アルゴリズムとは？】をご覧ください。

数学的剰余

数学的な剰余は、割り算の結果として残る余りが非負であり、除数より小さいという条件を満たします。
具体的には、次の式を満たすように余りを定義します。

$a=b×q+ra = b \times q + r$

• a は被除数（割られる数）
• b は除数（割る数）
• q は商（整数部分）
• r は余り（剰余）

ここで、余り r は次の条件を満たします：
$0≤r<∣b∣0 \leq r < |b|$

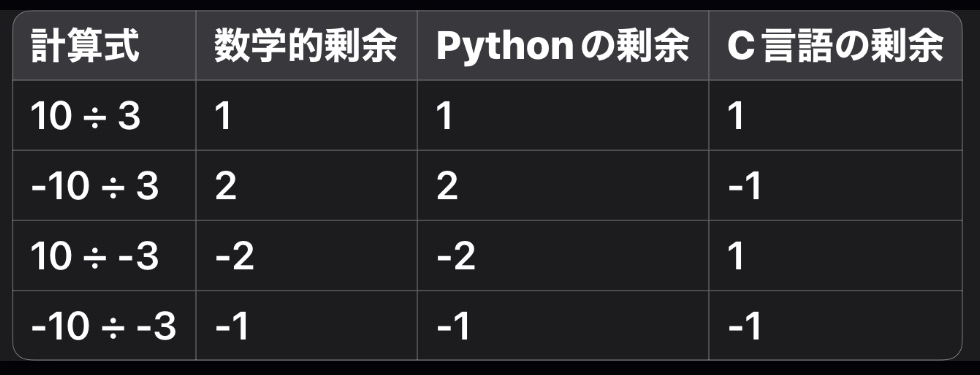
結論

• 数学的剰余は「非負の余り」を求めるのが基本だが、プログラミング言語では「演算の一貫性」や「ハードウェアの都合」によって異なる仕様が採用されている。
• CやJavaはハードウェアの都合を優先し、余りを「被除数と同じ符号」にする。
• PythonやRubyは数学的な整合性を重視し、余りを「除数と同じ符号」に調整する。

この違いを理解しておけば、言語間で剰余演算を使うときのバグを防ぐことができます。

---

4. まとめ

本記事では、ロジカル思考の代表例として演繹法と帰納法を取り上げ、それぞれの特徴とアルゴリズムへの応用について解説しました。

• 演繹法: 既存のルールを個別のケースに適用（例: 並べ替えのアルゴリズム、論理プログラミング）
• 帰納法: データからパターンを学習し、一般ルールを推測（例: 機械学習、経験則のアルゴリズム）

ロジカル思考を鍛えることで、より合理的なアルゴリズム設計や問題解決が可能になります。
ぜひ、日常のプログラミングに活かしてみてください！