Zenn
アルゴリズム×数学の学び直しPublicationへの投稿
🔀

並べ替えのアルゴリズム

zoldof
に公開
Python
プログラミング
AtCoder
学習
アルゴリズム
tech

予備知識

  • アルゴリズムとは？
  • 文章構成
    この記事で紹介するアルゴリズムの計算量について［最善，最悪，平均］の区別はありません。[1]
    空間計算量は例外的に記載します。[2]

はじめに

この記事では並べ替えのアルゴリズムの中で基本的なものを紹介します。
具体的には以下５つのソートアルゴリズム[3]です。

  1. バブルソート
  2. 選択ソート
  3. バケットソート
  4. 分布数え上げソート
  5. 基数ソート

並べ替えのアルゴリズムで出来ること

データ構造（配列）を昇順または降順に並べ替える

計算対象選別

判定 計算対象 関係 基準値
○ データの比較回数 ≧ データの交換回数
データの交換回数 = 配列の中身により異なる
関数の呼び出し回数 = 確定値の決定回数

共有変数定義

変数にする対象 変数 関係 数値
配列の最大要素数 n > 1
数値範囲 m[4]
比較回数の総和 S

バブルソート

このアルゴリズムでは隣接する２つの要素を順番に比較していくことで配列を並べかえる
その有り様が泡の動きに似ていることからバブルソートと呼ばれる
バブルソートには大きく分けて２種類ある
これは比較の基準が異なるからである

小降大昇のバブルソート

  • 最小値を基準として配列を降順🔽に並べ替え
    降順バブルソート
  • 最大値を基準として配列を昇順🔺に並べ替え
    昇順バブルソート

小昇大降のバブルソート

  • 最小値を基準として配列を昇順🔺に並べ替え
    最小値を基準とする昇順バブルソート
    ※黄色は要素の交換が発生する部分
  • 最大値を基準として配列を降順🔽に並べ替え
    最大値を基準とする降順バブルソート

バブルソートの一般化

配列の最大要素数が５のとき上記の表より
比較回数の総和Ｓは

S=(5-1)+(5-2)+(5-3)+(5-4)
一般化すると
S=T(n) なので
T(n)=(n-1)+(n-2)+(n-3)+(n-4)…
自然数の和の公式より
T(n)=\frac 1 2 n(n-1)[5]
漸近計算量は O(n^2) である

バブルソートの実装

# バブルソート
def bubble_sort(arr):
    n = len(arr)
    compare_count = 0
    swap_count = 0
    for i in range(n):
        for j in range(n - i - 1):
            compare_count += 1
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swap_count += 1
    return compare_count, swap_count, arr

選択ソート

このアルゴリズムでは比較している時点までの
最小値もしくは最大値を基準とするため
交換回数は確定値が決まるごとに最大でも１回ずつで済む
比較回数はバブルソートと同じである

  • 最小値を基準として配列を昇順🔺に並べ替え
    選択ソート昇順
  • 最大値を基準として配列を降順🔽に並べ替え
    選択ソート降順

選択ソートの一般化

バブルソートの一般化と同じになるため省略する

選択ソートの実装

# 選択ソート
def selection_sort(arr):
    n = len(arr)
    compare_count = 0
    swap_count = 0
    for i in range(n):
        min_index = i
        for j in range(i + 1, n):
            compare_count += 1
            if arr[j] < arr[min_index]:
                min_index = j
        if i != min_index:
            arr[i], arr[min_index] = arr[min_index], arr[i]
            swap_count += 1
    return compare_count, swap_count, arr

バブルソートと選択ソートの比較検証

同じ配列を小昇大降で並べ替えする場合

  • バブルソートでは確定値が決定するとき以外でも交換が発生するので交換回数は８回である
  • 選択ソートでは確定値が決定するときだけ交換が発生するので交換回数は４回である

よって選択ソートはバブルソートと比べて交換回数が少ない

それぞれの実行結果

プログラム出力の例（データ個数が1000個の場合）
【Bubble Sort】
  比較回数: 499500
  交換回数: 258017
  実行時間: 6.484427 秒
  メモリ使用（現在）: 8144 bytes
  メモリ使用（ピーク）: 8420 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

【Selection Sort】
  比較回数: 499500
  交換回数: 988
  実行時間: 3.113328 秒
  メモリ使用（現在）: 8064 bytes
  メモリ使用（ピーク）: 8364 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

実行時間を考慮すると、選択ソートの方が有利です。
なぜなら、選択ソートは交換の回数が少ないため、処理全体が速く終わる傾向があるからです。
特に、データの件数が多くなって実用レベルのプログラムになったときには、バブルソートよりも選択ソートの方が効率的だと言えます。

バケットソート

このアルゴリズムを使うには前もって配列の要素に入る数値の範囲が分かっている必要がある

例えば１～５であると分かっている場合には
まずバケツを５つ用意して１～５の番号を記入する

そして配列を先頭の要素から順番に比較していき
要素内の数値を確認して用意されたバケツのうち同じ番号のバケツに分別していく

ここで言う用意されたバケツが数値範囲に該当する
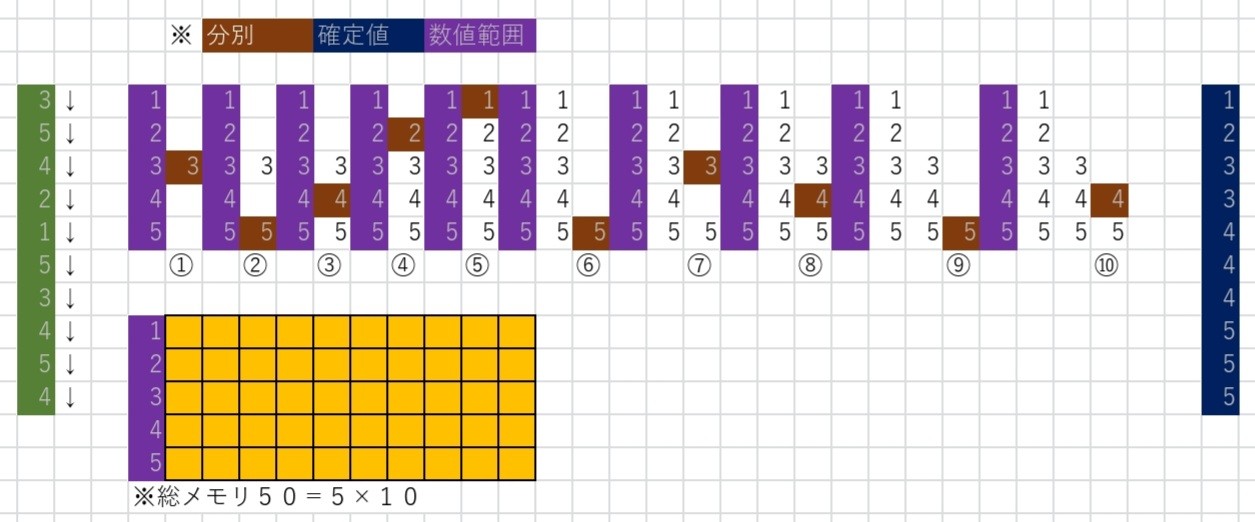
昇順バケットソートの例

バケットソートの一般化

表のとおり
T(n)=n
漸近計算量は O(n) である
空間計算量として nm が必要である

バケットソートの実装

# バケットソート
def bucket_sort(arr):
    buckets = [[] for _ in range(max_val + 1)]
    for num in arr:
        buckets[num].append(num)
    index = 0
    for bucket in buckets:
        for num in bucket:
            arr[index] = num
            index += 1
    return 0, 0, arr

分布数え上げソート

このアルゴリズムを使うには前もって配列の要素に入る数値の範囲が分かっている必要がある

基本的な構造はバケットソートに似ているが数値範囲としてバケツではなくキー[6]を使う
バケツに番号を記入するのは同じで配列の要素を分別したときに個数を記録していくことが特徴である

すべての記録が終了したら記録された個数をもとに配列の並べ替えを完了する
昇順分布数え上げソートの例

分布数え上げソートの一般化

記録終了までの比較と記録終了後のキーを参照する回数を足し合わせた計算量がかかる

具体的には比較はｎ回で参照はｍ回なので
T(n)=n+m
漸近計算量は O(n+m) である
空間計算量として n+m が必要である

分布数え上げソートの実装

# 分布数え上げソート
def counting_sort(arr):
    count = [0] * (max_val + 1)
    for num in arr:
        count[num] += 1
    index = 0
    for val in range(len(count)):
        for _ in range(count[val]):
            arr[index] = val
            index += 1
    return 0, 0, arr

バケットソートと分布数え上げソートの比較検証

  • バケットソートは、時間計算量だけで見ると高速だが、そのぶん 空間計算量が大きくなりやすい という特徴がある。特にバケツの数をデータ数に合わせて確保する必要があるため、メモリ使用量が増えがち。
  • 分布数え上げソートは、数値範囲が狭い場合に非常に効率的で、高速かつ安定して動作する。ただし、数値範囲が広がると 大きな配列を確保する必要があり、空間効率が悪くなる ことがある。

実際のメモリ使用量まで含めて評価するなら、分布数え上げソートのほうが実用上優れています。

それぞれの実行結果

プログラム出力の例（データ個数が1000個の場合）
【Bucket Sort】
  比較回数: 0
  交換回数: 0
  実行時間: 0.002660 秒
  メモリ使用（現在）: 12480 bytes
  メモリ使用（ピーク）: 93472 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

【Counting Sort】
  比較回数: 0
  交換回数: 0
  実行時間: 0.019023 秒
  メモリ使用（現在）: 23552 bytes
  メモリ使用（ピーク）: 31728 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

分布数え上げソートは、メモリ使用量が少なく、範囲さえ限定されていれば高速で安定して動作します。
一方、バケットソートは一見高速に見えますが、膨大なメモリを消費するため実用性は低めです。
上記のデータを参考に計算してみます。
たとえば100万人のユーザーがいるゲームアプリでランキングを並べ替えると、バケットソートでは64MB近くメモリを消費します。
これはあくまでランキングだけの話で、画像や音声、通信処理も含めると、とても実用的とは言えません。

基数ソート

基数とは数値のもとになるもので０～９の数字である
基数を用意して配列を先頭から分別していく

配列の要素の桁数の数だけ分別を繰り返す
一の位から順番に分別することで並べ替えが完了する
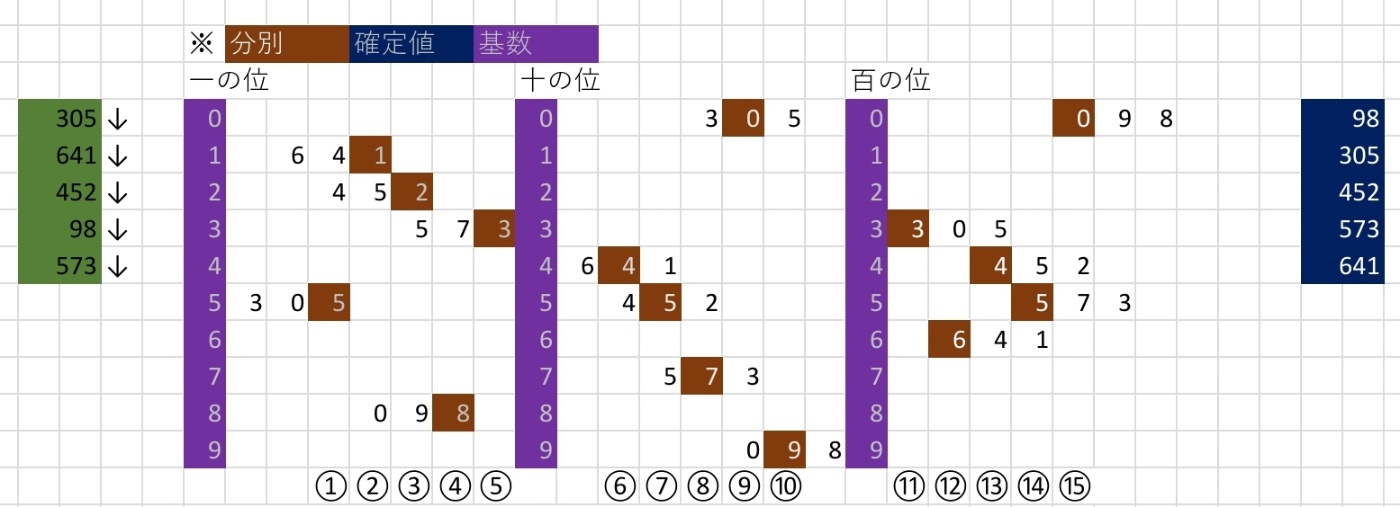
昇順基数ソートの例
計算量が分かりやすいように比較順番（最下部番号）に合わせた表になっている

実際には各基数のところに配列の各要素が縦ならびで並べ替えられていく
各位の数で同じ数字であるときは先に分別した方から左側に詰めて並べる

例えば4つ要素[502,301,100,501]の1の位だけ並べ替えると以下のようになる

基数 優先席 次席
0 100
1 301 501
2 502

基数ソートの一般化

表のとおり
T(n)=nm
漸近計算量は O(nm) である
空間計算量として基数分の 10[7]が必要である

基数ソートの実装

# 基数ソート
def radix_sort(arr):
    max_digit = len(str(max_val))
    output = arr[:]
    for d in range(max_digit):
        buckets = [[] for _ in range(10)]
        for num in output:
            digit = (num // (10 ** d)) % 10
            buckets[digit].append(num)
        output = [num for bucket in buckets for num in bucket]
    return 0,0, output

基数ソートの実行結果

プログラム出力の例（データ個数が1000個の場合）
【Radix Sort】
  比較回数: 0
  交換回数: 0
  実行時間: 0.017508 秒
  メモリ使用（現在）: 8800 bytes
  メモリ使用（ピーク）: 34632 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

５つのソートアルゴリズムのまとめ

一般式

種類 漸近記法 実際記法 空間計算量 条件
バブルソート O(n^2) \frac 1 2 n(n-1) 無視 n>1
選択ソート 同上 同上 同上 同上
バケットソート O(n) n nm 同上
分布数え上げソート O(n+m) n+m n+m 同上
基数ソート O(nm) nm 10 同上

一般式のみで見た結論

  • 理想的な条件で最も高速なのは［バケットソート］や［分布数え上げソート］
  • 安定して速いが、前提条件を選ぶのは［基数ソート］
  • 汎用性はあるが遅いのは［バブルソート］［選択ソート］
  • メモリを節約したいなら［バブルソート］か［選択ソート］

実行結果

すべての結果まとめ
プログラム出力の例（データ個数が1000個の場合）
【Bubble Sort】
  比較回数: 499500
  交換回数: 258017
  実行時間: 6.484427 秒
  メモリ使用（現在）: 8144 bytes
  メモリ使用（ピーク）: 8420 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

【Selection Sort】
  比較回数: 499500
  交換回数: 988
  実行時間: 3.113328 秒
  メモリ使用（現在）: 8064 bytes
  メモリ使用（ピーク）: 8364 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

【Bucket Sort】
  比較回数: 0
  交換回数: 0
  実行時間: 0.002660 秒
  メモリ使用（現在）: 12480 bytes
  メモリ使用（ピーク）: 93472 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

【Counting Sort】
  比較回数: 0
  交換回数: 0
  実行時間: 0.019023 秒
  メモリ使用（現在）: 23552 bytes
  メモリ使用（ピーク）: 31728 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

【Radix Sort】
  比較回数: 0
  交換回数: 0
  実行時間: 0.017508 秒
  メモリ使用（現在）: 8800 bytes
  メモリ使用（ピーク）: 34632 bytes
  ソート後の配列: [0, 1, 1, 2, 2, 2, 8, 8, 8, 11]

実測結果を見ると、選択ソートはメモリ使用量が少なく、実行時間も比較的短いアルゴリズムでした。
ほかのソートもそれぞれに特長があり、データの性質や用途に応じて適切に使い分けることができます。
状況に応じて最適な手法を選ぶ視点が大切です。

脚注

  1. アルゴリズムの途中で昇順降順を確認する場合、そもそもソートの中でソートすることが基本的に矛盾しており、余分な計算量がかかる。途中で止めて計算量を測定することに意味がないから、すべて最悪の計算量として認識する ↩︎

  2. ［バケット，分布数え上げ］ソートについては、空間計算量が大きいため例外的に記載する。基数ソートについても空間計算量は小さく無視できるものの、上記２つに関連するため記載する ↩︎

  3. ソートとは並べ替えを意味する横文字のこと ↩︎

  4. 配列の数値範囲である。基数ソートの場合は配列の最大値の桁数を意味する ↩︎

  5. 公式を元の形のまま適用するためには例の場合で総和が１～４までの和と捉えると分かりやすい。自然数の和は\frac 1 2 x(x+1)であるが、このxが5-1=4であると捉える ↩︎

  6. 個数を記録する鍵的な仕組みから数値範囲を「キー」と呼ぶ ↩︎

  7. 例えば、すべての要素の下2桁が同じ場合、バケットソートのように膨大な空間計算量が必要になるが、ここでは例外的な位置付けである ↩︎

アルゴリズム×数学の学び直し
アルゴリズム×数学の学び直しPublication

このパブリケーションでは、アルゴリズムの理解を深めるために必要な数学を基礎から学び直します。算数・数学の基本概念から始め、実践的なアルゴリズムの活用までを丁寧に解説。初心者から学び直したい方、プログラミングやデータ構造に興味がある方に向けた内容をお届けします。

Discussion