数値探索のアルゴリズム

予備知識

• アルゴリズムとは？
• 文章構成

線形探索

このアルゴリズムで出来ること

データ構造から特定の値を探索する
※ここでデータ構造は配列とする

動作順序

①配列の先頭から順に要素を選択する
②その要素が特定値であるか比較する

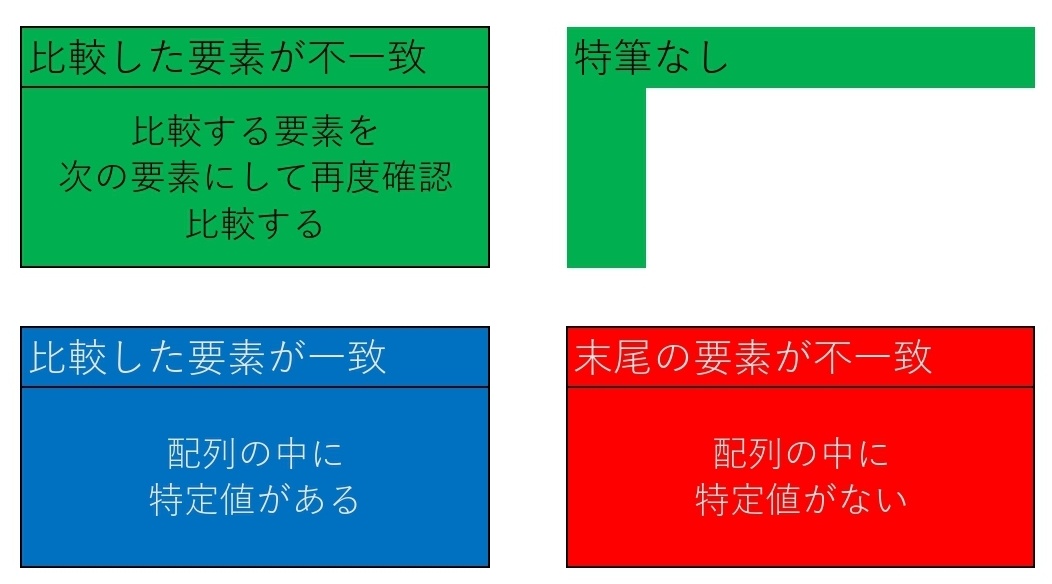
計算対象選別

判定	計算対象	関係	数値
○	データの比較回数	≧	1
	データの交換回数	=	0
	関数の呼び出し回数	=	0

変数定義

変数にする対象	変数	関係	数値
配列の最大要素数	$n$	>	1

一般化

最善の計算量

最善の計算量となるのは
配列の先頭の要素が特定値のときである
このときのデータの比較回数すなわち計算量は
$T(n)=1$
漸近計算量は $O(1)$ である

---

最悪の計算量

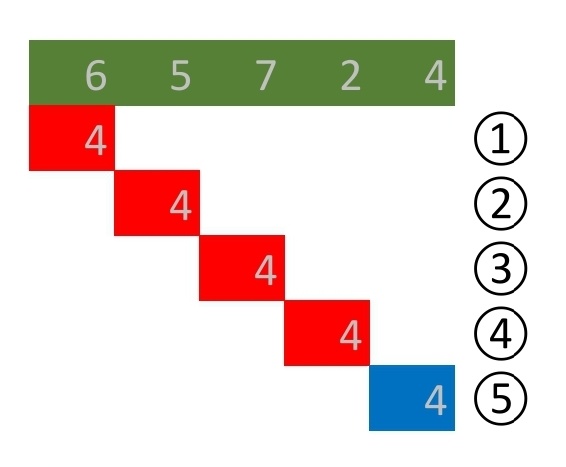
最悪の計算量となるのは
配列の末尾の要素が特定値のときである
このときのデータの比較回数すなわち計算量は
$T(n)=n$
漸近計算量は $O(n)$ である

---

平均の計算量

配列の最大要素数が５のとき
特定値は配列の要素の１つ目から５つ目までのいずれかの５通りである
よって自然数１～５の平均値が平均の計算量である

$$\frac {1+2+3+4+5} 5 =3$$

ある範囲の自然数の平均は中央値でもある
この場合の中央値を求めるには範囲の先頭と末尾の数値を足して半分にする

$$\frac {1+5} 2 =3$$

この式を一般化すると

$T(n)=\frac {1+n} 2$
漸近計算量は $O(n)$ である

確かめ算

$n$	$T(n)$
5	3
6	3.5
7	4
8	4.5

---

一般式の一覧表

---

二分探索

このアルゴリズムで出来ること

昇順または降順のデータ構造から特定の値を探索する
※ここでデータ構造は配列とする
※比較する範囲が半分ずつ減っていく

動作順序

①配列のすべての要素を比較範囲に設定する
②配列の中央の要素が特定値であれば完了とし異なる場合は③へ
③以下の条件で新たな比較範囲を設定して②に戻る

• 配列の中央の要素が特定値より大きければ比較範囲の先頭から中央までの要素
• 配列の中央の要素が特定値より小さければ比較範囲の中央から末尾までの要素

※配列の要素数が偶数個のときは中央の要素２つのうち１つ目を中央とする

計算対象選別

判定	計算対象	関係	数値
○	データの比較回数	≧	1
	データの交換回数	=	0
	関数の呼び出し回数	=	0

変数定義

変数にする対象	変数	関係	数値
配列の最大要素数	$n$	>	1

一般化

最善の計算量

最善の計算量となるのは
配列の中央の要素が特定値のときである
このときのデータの比較回数すなわち計算量は
$T(n)=1$
漸近計算量は $O(1)$ である

---

最悪の計算量

最悪の計算量となるのは
要素が最後のひとつになるまで分割が必要なときである
この比較回数は最初の１回に要素の分割回数を足したものである

よって計算量は
$T(n)=\log {(n)} +1$
漸近計算量は $O(\log n )$ である

確かめ算

$n$	$T(n)$	推移
2	2	$n$ が 3 まで同値
4	3	$n$ が 7 まで同値
8	4	$n$ が 15 まで同値
16	5	$n$ が 31 まで同値

---

平均の計算量

配列の要素がｎ個の比較回数一覧

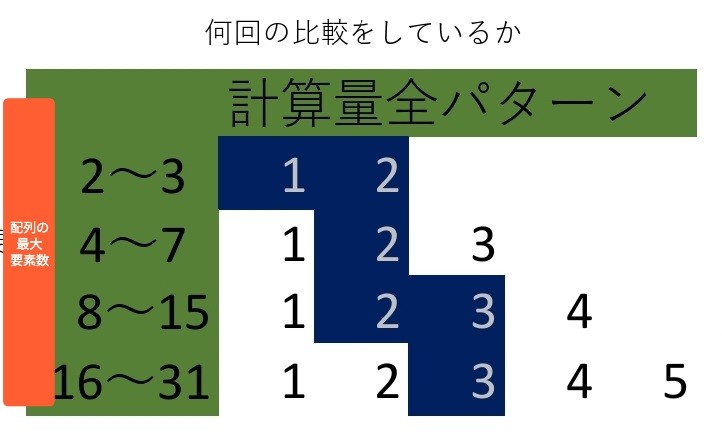
配列の最大要素数が１６～３１のとき
計算量は１から５までのいずれかの５通りである
よって自然数１～５の平均値が平均の計算量である

$$\frac {1+2+3+4+5} 5 =3$$

ある範囲の自然数の平均は中央値でもある
この場合の中央値を求めるには範囲の先頭と末尾の数値を足して半分にする

$$\frac {1+5} 2 =3$$

この式を一般化すると
第一項が最善の計算量で第二項が最悪の計算量となっているので

$T(n)=\frac {1+(\log n +1)} 2$
↓
$T(n)=\frac {\log n} 2 +1$
漸近計算量は $O(\log n )$ である

確かめ算

$n$	$T(n)$
2	1.5
4	2
8	2.5
16	3

---

一般式の一覧表