数値処理のアルゴリズム

予備知識

• アルゴリズムとは？
• 文章構成

配列値比較計算

配列について簡単な理解を得るならば、現実世界ではコインロッカーが近しい存在です。
横に５つ、縦に５つの保管場所を持つコインロッカーなのだとしたら、配列で言うところの５行５列という意味合いになります。
また、これは数学で言う行列の表現方法と同じです。
配列はアルゴリズムを理解するにあたっての基本的な知識になります。
配列という単語は、配列で選択中の要素か、すべての要素を指しています。
なぜ、そのような曖昧な表現になるかと言えば、配列の種類によって要素の最大個数が確定していない場合があるからです。
要素の最大個数のことを最大要素数と呼びます。

• 単語のつながりで使用例を見ると
  「『配列』の『要素』に『値』を代入する」となります。
  ※値とは数値や文字列のことです。
• コインロッカーに言い換えるなら
  「『コインロッカー』の『保管場所』に『物』を入れる」となります。

各単語の意味をつながりで覚えると記憶しやすいです。

このアルゴリズムで出来ること

配列の要素に値を代入しながら同時に要素比較を行う過程を視覚的に理解する

動作順序

①表の個数１の行かつ最右端Ｌ列の配列要素を選択している状態とする
②２桁の乱数を生成し選択している要素に代入する
③現在列の配列要素のうち数値が代入された要素すべての［合計，平均，最大，最小］を求める
④選択要素の行をひとつ下へ列をひとつ左へ移動する
⑤選択要素が配列の要素であれば②へ戻る

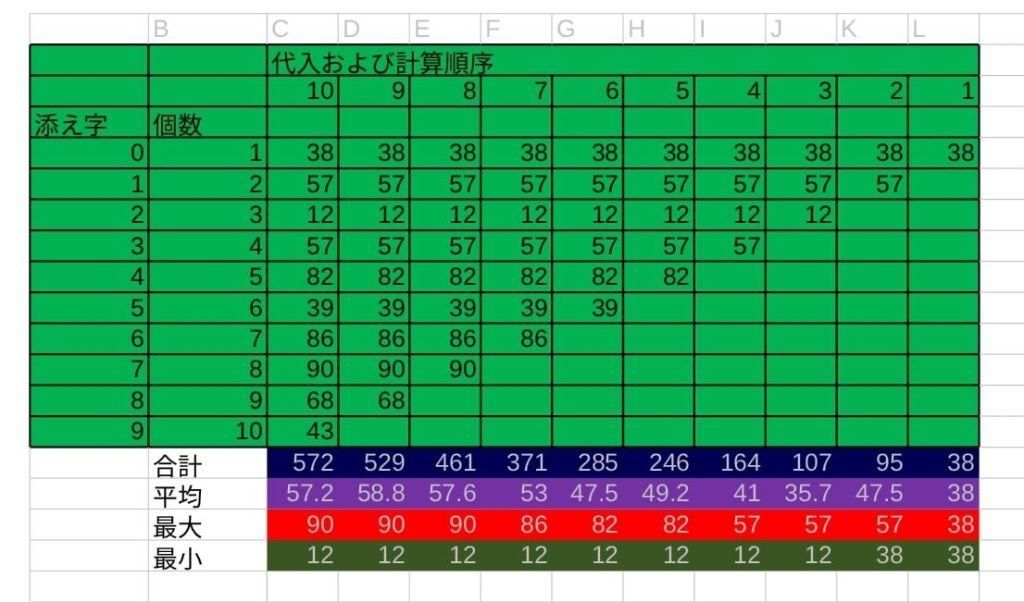
表のように、配列要素の数え方を個数で表現するほか、添え字でも表現可能です。
「添え字」とはプログラミングで用いられる表現で、要素１個目が添え字０となります。
もし、混同してややこしい場合には以下の方法で対応します。

• 添え字０の要素を飛ばす
• 配列の仕様を変更し添え字１からの開始として指定する

計算対象選別

判定	計算対象	関係	数値
	データの比較回数	=	0
	データの交換回数	=	0
○	関数の呼び出し回数	=	1

変数定義

変数にする対象	変数	説明
配列	$a[9]$	最大要素数が１０個の配列
合計	$sum$
平均	$ave$
最大	$max$
最小	$min$

一般化

計算量としては動作順序にあるような処理を行う関数を１回呼び出すことに等しいので
$T(n)=1$
漸近計算量は $O(1)$ である

配列値比較計算のアルゴリズムで空間計算量の補助空間は時刻の［合計，平均，最大，最小］の領域分で４、空間の複雑さは配列の最大要素数１０となります。
このように、配列値比較計算では時間計算量より空間計算量が大きくなりますが、ほとんどのアルゴリズムで無視するので記載しません。
すべてのアルゴリズムで一貫性を持たせ、様々なアルゴリズム同士を比較しやすくするためです。
以降、他アルゴリズムの計算量についても同様の認識で理解してください。

時刻差分

ここではデジタル時計の時刻表示をとりあげます。

このアルゴリズムで出来ること

$00:00:00$ の形式で指定された２つの時刻の差分を求める

動作順序

①２つの指定時刻をそれぞれ［時間，分，秒］に分ける
②２つの時刻の［時間の差，分の差，秒の差］を求める
③時間差を３６００倍，分差を６０倍する
④すべての差を合計すると［秒］の時刻差分が求まる
⑤時刻表示とするため、まずは差分を３６００で割り、その商が［時間］部分になる
⑥つぎに、⑤で時刻差分を３６００で割った余りの方をあらたに時刻差分とする
⑦さらに、この時刻差分を６０で割った商が［分］部分になる
⑧最後に、この時刻差分を６０で割った余りが［秒］部分になる

計算対象選別

判定	計算対象	関係	数値
	データの比較回数	=	0
	データの交換回数	=	0
○	関数の呼び出し回数	=	1

変数定義

変数にする対象	変数	時間	分	秒
１時間	$h$	$1×h$	$60×h$	$60×60×h$
１分間	$m$		$1×m$	$60×m$
１秒間	$s$			$1×s$
１つ目の時刻	$a_1$
２つ目の時刻	$a_2$
秒の時刻差分	$S_t$

一般化

1つ目の時刻の秒部分は $s(a_1)$ は $00:00:00$ の形式で下２桁にあたる部分であり
それをふまえて１つ目の時刻全体を秒であらわすと

$$a_1=[60×60×h(a_1)]+[60×m(a_1)]+[1×s(a_1)]$$

共通因数でくくると

$$a_1=60\{[60×h(a_1)]+m(a_1)\}+s(a_1)$$

同様に２つ目の時刻を秒であらわすと

$$a_2=60\{[60×h(a_2)]+m(a_2)\}+s(a_2)$$

$a_2>a_1$ のとき $S_t=a_2-a_1$ なので

$$S_t=60\{⟮60×[h(a_2)-h(a_1)]⟯+[m(a_2)-m(a_1)]\}+[s(a_2)-s(a_1)]$$

ここまでで秒の時刻差分が求まり
これは $00:00:00$ の形式で言うと以下のようになる

$${\frac {S_t} {3600}\ 時間\ \frac {S_t\%3600} {60}\ 分\ (S_t\%3600)\%60\ 秒}$$

この式は計算量を指し示しておらず時刻差分を求めるための文字式でしかない

別途で計算量を表現するならば上記のように

• 秒の時刻差分 $S_t$ を求める
• 求めた時刻差分を時刻表示にして出力する

この２つの処理が可能な関数を呼び出すことになる
※ここで関数の引数は２つの時刻 $a_1$ と $a_2$ である

よって計算量としては関数を１回呼び出すことに等しいので
$T(n)=1$
漸近計算量は $O(1)$ である

最大公約数

数学的な「最大公約数を求める」と結果的には同じ意味合いである［ユークリッドの互除法］をとりあげます。

このアルゴリズムで出来ること

ユークリッドの互除法で最大公約数を求める流れを視覚的に理解する

動作順序

①最大公約数を求めたい２つの数値のうち、大きい数値を割られる側、小さい数値を割る側として割り算する
②あらたに小さい数値を割られる側、①の余りを割る側として割り算する
③あらたに①の余りを割られる側、②の余りを割る側として割り算する
④ここまでの計算過程のなかで余りが０になった時点での割る数が最大公約数となる
※③の余りが０にならない場合には③同様に（２順序前の余り）から（１順序前の余り）を割った余りが０になるまで同じ処理を繰り返す

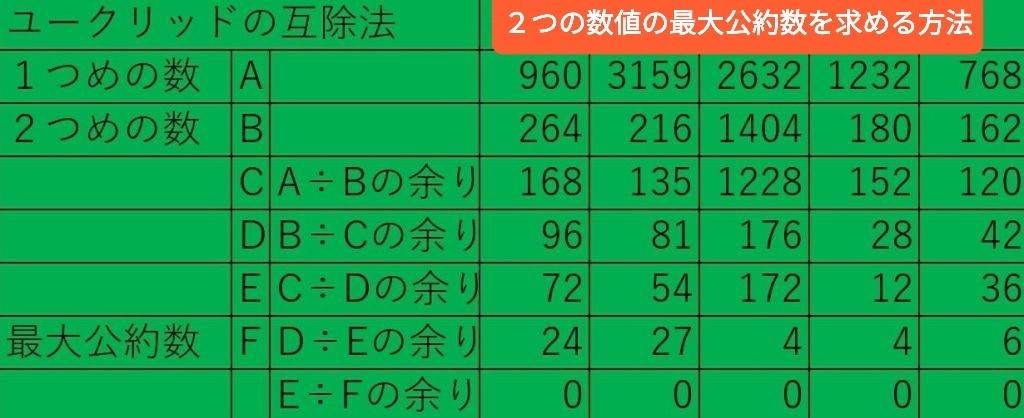
※この表では例として、２つの数値を５組選出して記載しました。

計算対象選別

判定	計算対象	関係	数値
	データの比較回数	=	0
	データの交換回数	=	0
○	関数の呼び出し回数	=	1

変数定義

変数にする対象	変数
１つ目の数値	$a$
２つ目の数値	$b$
割り算の結果	$c$

一般化

計算量としては動作順序にあるような処理を行う関数を１回呼び出すことに等しいので
$T(n)=1$
漸近計算量は $O(1)$ である