文字列検索のアルゴリズム
予備知識
はじめに
この記事では文字列検索のアルゴリズムを3つ紹介します。
- 力まかせ法
- KMP法
- BM法
文字列検索のアルゴリズムで出来ること
ある文字列の中に指定された文字列が含まれるか調べる
※以降は「ある文字列」のことを「テキスト」と呼ぶ
※同様に「指定文字列」のことを「パターン」と呼ぶ
計算対象選別
| 判定 | 計算対象 | 関係 | 数値 |
|---|---|---|---|
| ○ | データの比較回数 | > | 1 |
| データの交換回数 | = | 0 | |
| 関数の呼び出し回数 | = | 0 |
共通変数定義
| 変数にする対象 | 変数 | 関係 | 値 |
|---|---|---|---|
| テキストの文字数 | > | ||
| パターンの文字数 | > | 1 |
※パターンは文字列なので1より大きい
力まかせ法
テキストの先頭からパターンと一致する部分があるか
パターンを1文字ずつずらして確認していく
力技との意味合いで力まかせ法と呼ばれる
動作順序
①テキストとパターンを左揃えにする
②テキストの比較開始位置をテキストの先頭の文字とする
③テキストとパターンを各文字列の左側から順番に比較する
④パターンが見つかれば終了し不一致の時点でパターンを1文字ずらして③へ戻る
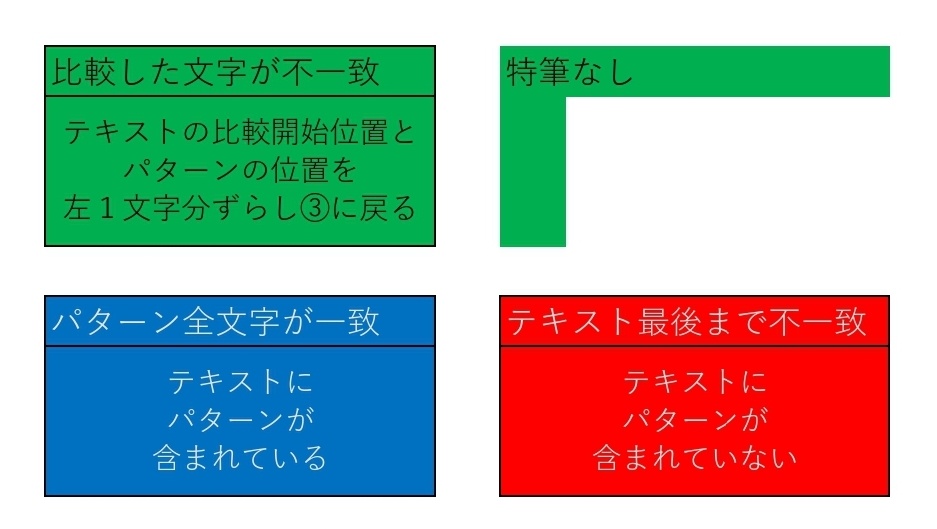
変数定義
| 変数にする対象 | 変数 | 関係 | 値 |
|---|---|---|---|
| パターンの比較繰り返し回数 | = | ||
| 文字列一致の組み合わせの総数 | |||
| すべての組み合わせにおける計算量の総和 |
一般化
最善の計算量
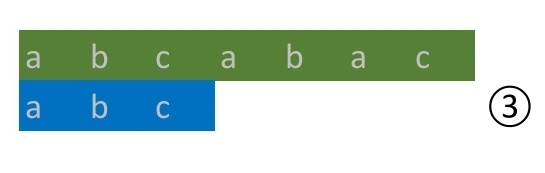
最善の計算量となるのは
テキストの最初でパターン全文字が一致したときである
このときのデータの比較回数は
漸近計算量は
最悪の計算量

最悪の計算量となるのは
テキストの末尾文字手前までおなじ文字がつづき
テキストの末尾文字確認時にようやくパターンとの一致が確認できるときである
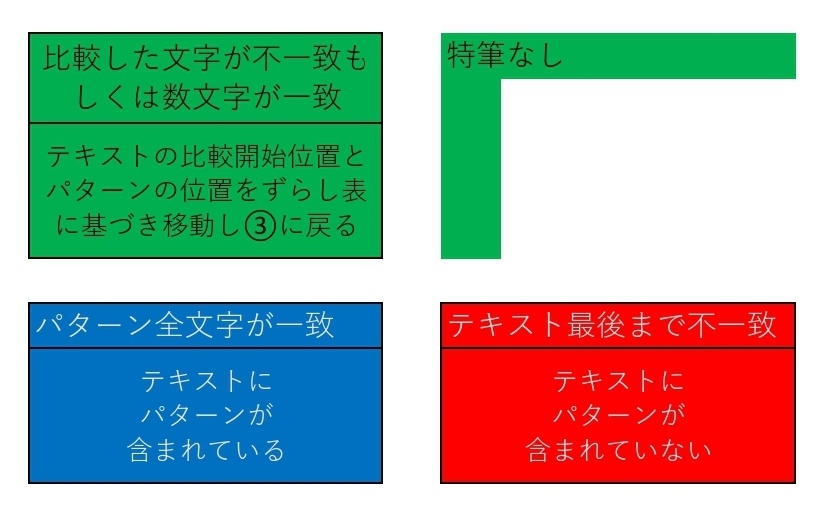
比較した文字が不一致のとき
テキストの比較開始位置とパターンの位置を右にずらす必要があり
そのたびにパターンの文字数分の比較が必要になるため計算量が多くなる
合計で何回ずらすかというと
テキストの文字数からパターンの文字数を引いた数なので
その比較回数の合計は
よって
漸近計算量は
確かめ算
| 5 | 15 |
| 4 | 16 |
| 3 | 15 |
| 2 | 12 |
※nが7のとき
平均の計算量
最悪の計算量においては
パターンをずらす前も含めて
平均の計算量においては
この文字数分の比較のいずれかの段階で一致する場合が想定できる
そこでそれぞれの場合がどういった形で一致するのか調べる必要があるので
- まずは文字列一致の組み合わせの総数を求める
- 次にすべての組み合わせにおける計算量の総和を求める
- 最後に総和を総数で割り算して平均の計算量を求める
※以降はそれぞれを「総数」「総和」と呼ぶこととする
ずらし過程は行列の行追加と似ているので行列と同様に扱うものとして
テキストの文字数が5でパターンの文字数が3の例を表にすると
| 1 | 2 | 3 | 4 | 5 | 組み合わせ |
|---|---|---|---|---|---|
| ○ | ○ | ○ | ○ | ○ | |
| a | b | c | 1 | ||
| ○ | ○ | ○ | ○ | ○ | |
| a | b | c | |||
| a | b | c | |||
| ○ | ○ | ○ | ○ | ○ | |
| a | b | c | |||
| a | b | c | |||
| a | b | c |
このようにテキストとパターンの文字列によって行数に違いが生じる
これは行数が増えると計算量が増えることを意味している
また各行での比較回数もテキストの文字列によって異なり1~3のいずれかになる
※何文字目で不一致となるかが異なるから
ということは行が追加されるたびに組み合わせが3倍されることになる
一般化した組み合わせを数列で表にすると
| 項 | 1 | 2 | 3 | … | k |
|---|---|---|---|---|---|
| 組み合わせ | … |
※この表での数列の「項」が前述の「行」と同値である
※「行」は「パターンの比較繰り返し回数」のことである
総数はこの等比数列の和なので
前述の例の場合における計算量を表にすると
| 項 | 1 | 2 | 3 |
|---|---|---|---|
| 組み合わせ | |||
| 計算量 |
数列の第1項の計算量は3であり
数列の第2項の計算量は第1項の計算量のひとつに対して1~3のいずれかが足された数値となり
数列の第3項の計算量は第2項の計算量それぞれに対して1~3のいずれかが足された数値となる
すべての組み合わせにおける計算量を一般化して表にすると
| 項 | 1 | 2 | 3 | … | k |
|---|---|---|---|---|---|
| 組み合わせ | … | ||||
| 計算量 | … |
行が増えるごとに最低でも1回は余分に比較しないと次の行に移動できないので各項の最小値は1ずつ増加する
各項の最大値は各行までの最大の計算量と見立てることができるのでパターンの文字数ずつ増加する
各項は組み合わせから行追加ごとm倍の分布になり均一に並ぶ
※例の計算量の表の通りである
よって中央値が各組み合わせの数だけ配されていることと同じである
数列の一般項の最小値と最大値から中央値を求めると
| 項 | 1 | 2 | 3 | … | k |
|---|---|---|---|---|---|
| 組み合わせ | … | ||||
| 計算量 | … | ||||
| 中央値 | … |
組み合わせと中央値から総和を求める
その前に各中央値の式の末項に注目するとそれぞれ
これらを組み合わせと掛け算して合計すると総数を引くことに等しいので総和は
よってkをnとmの式に戻して総和を総数で割り算する[1]と
近似式[2]は
漸近計算量は
一般式の一覧表
| 種類 | 漸近記法 | 実際記法 | 条件 |
|---|---|---|---|
| 最善 | |||
| 最悪 | 同上 | ||
| 平均 | 同上 | 同上 |
KMP法
力まかせ法より計算量を減らすために効率化したアルゴリズム
パターンの文字列を記憶することで文字ずらし分の計算量を削減している
アルゴリズム開発者3名の名前が由来である
動作順序
①テキストとパターンを左揃えにする
②テキストの比較開始位置をテキストの先頭の文字とする
③テキストとパターンを各文字列の左側から順番に比較する
④パターンが見つかれば終了し不一致の時点でパターンを適量ずらして③へ戻る
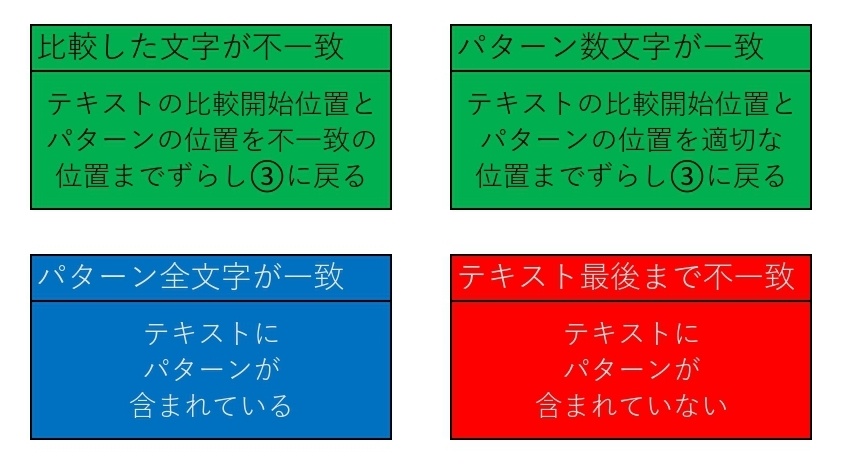
一般化
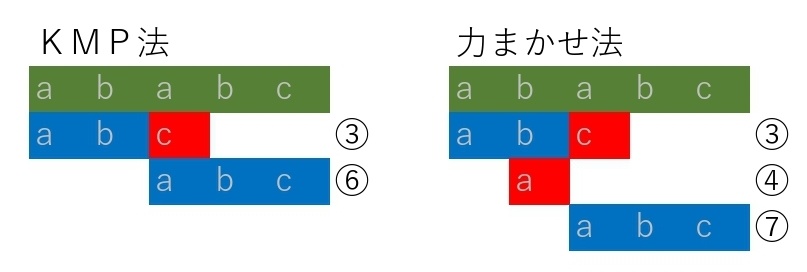
テキストとパターンがどういった文字列かによって変わるためここでは省略する
そのかわりに得意な文字列の組み合わせを記載する
KMP法が得意な文字列の組み合わせ
組み合わせの前提条件
- パターンの文字数が3文字以上
- パターンの末尾で不一致となる
この前提から2種類に分岐する
-
不一致文字がパターンに含まれない文字であるとき

-
不一致文字がパターンの先頭の文字であるとき
BM法
KMP法よりも計算量を減らすため効率化したアルゴリズム
パターンの文字列を記憶することで文字ずらし分の計算量を削減
さらにパターンの末尾から比較することで計算量を削減している
アルゴリズム開発者2名の名前が由来である
動作順序
①テキストとパターンを左揃えにする
②テキストの比較開始位置をパターンの末尾の位置とする
③テキストとパターンをパターンの右側から逆順に比較する
④パターンが見つかれば終了し不一致の時点でパターンをずらし表をもとにずらして③へ戻る
ずらし表の条件
ずらし表の条件には2種類ある
-
パターンの文字に重複がないとき
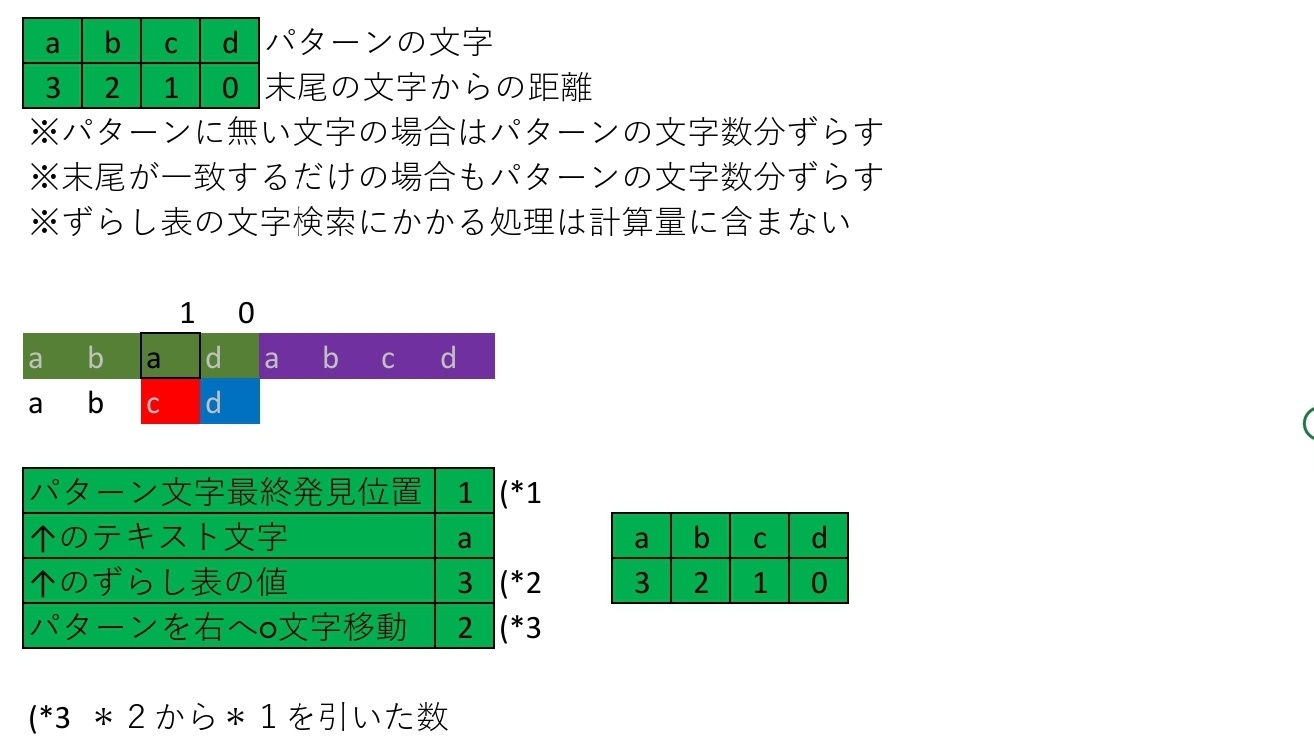
※ずらし表の実装には連想配列の使用を想定しているので、ずらし表の文字検索にかかる計算量がかからない仕様である
-
パターンの文字に重複があるとき

具体例
例えば下表のようなパターンの文字重複のときには
最終比較位置2までにaとbの2つの文字が一致して
そのうえaとbはパターンの末尾から3文字目以降に含まれる
そこでずらし量が最小になるaの値を適用する形になる
| 3 | 2 | 1 | 0 | |||
|---|---|---|---|---|---|---|
| a | c | a | b | a | a | b |
| b | a | a | b | |||
| a | c | a | b | a | a | b |
| b | a | a | b |
最終比較位置以降でずらし表に対応する位置から
最終比較位置以前で最後にaを発見した位置を引くので
この文字列比較における最初のずらし量は
一般化
テキストとパターンがどういった文字列かによって変わるためここでは省略する
そのかわりに得意な文字列の組み合わせを記載する
BM法が得意な文字列の組み合わせ
組み合わせの前提条件
- テキストの文字数がパターンの2倍以上
- パターンの末尾にあたるテキストの文字がパターン内で重複しない
この前提から2種類に分岐する
-
パターンの末尾が不一致したとき
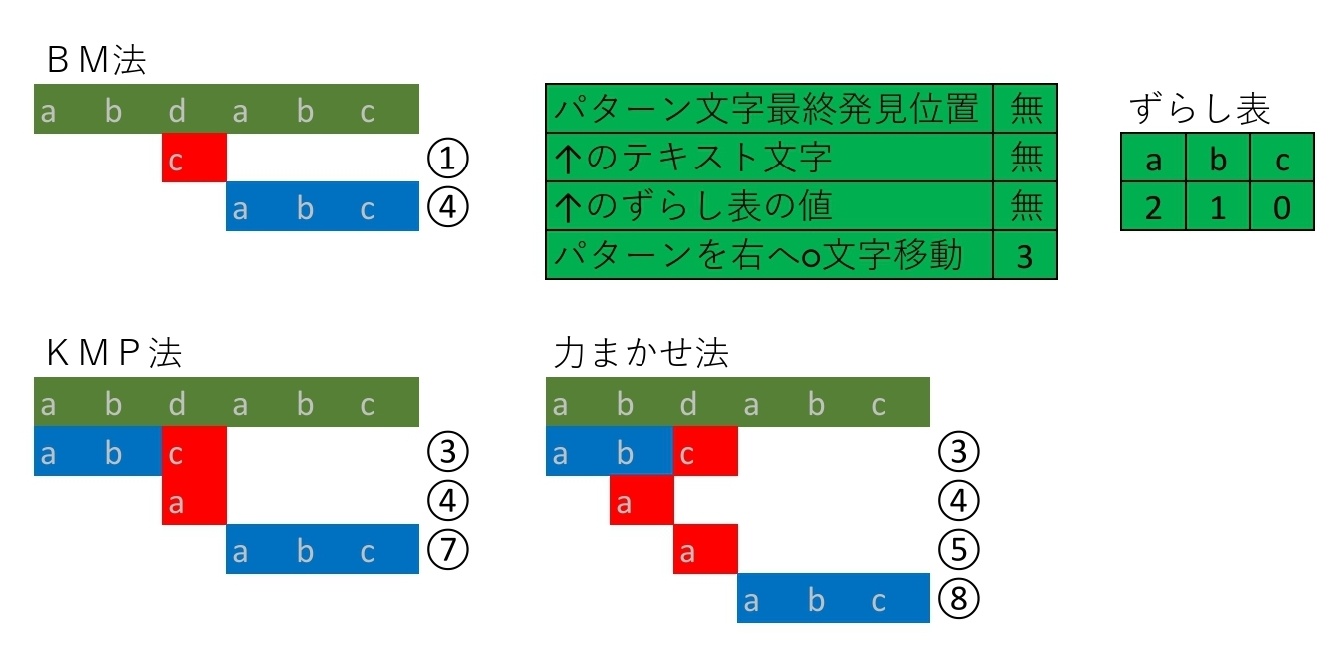
-
パターンの末尾のみ一致したとき
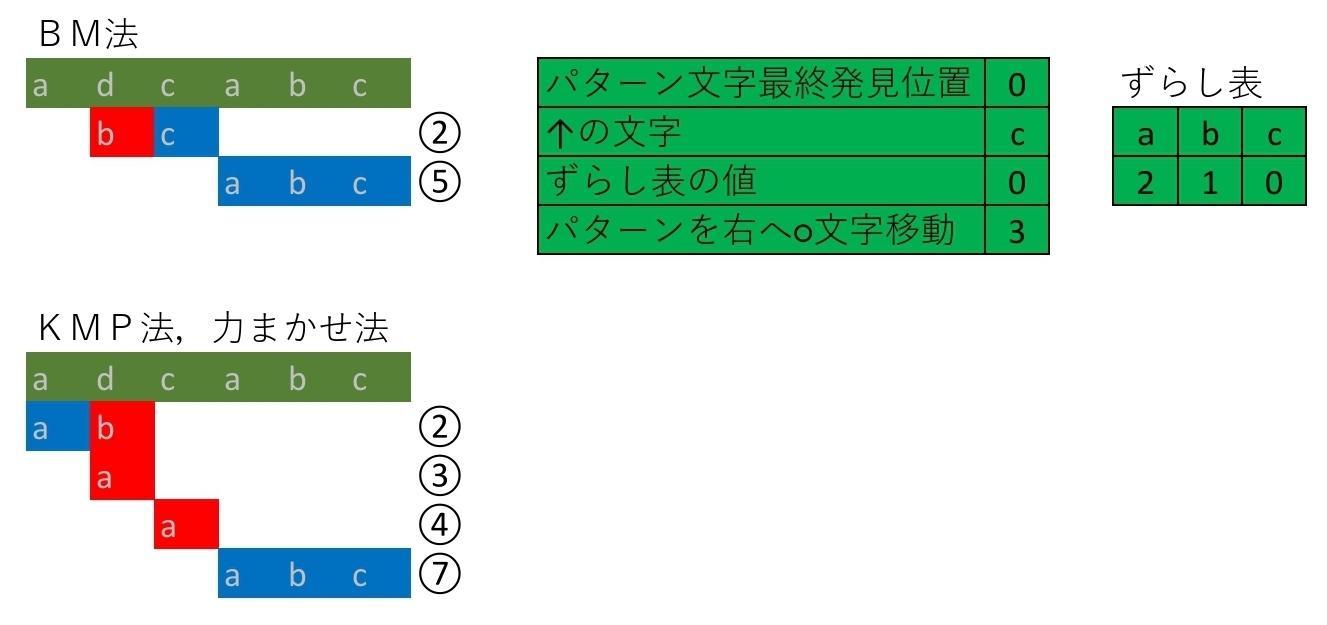
Discussion