統計的仮説検定を味わう: 検定手法の疑問解決からASA声明まで

はじめに

こんにちは。ZENKIGENデータサイエンスチーム所属のredteaです。原籍はオムロンソーシアルソリューションズ株式会社 技術創造センタですが、社外出向でZENKIGENに所属しており、数理最適化や機械学習を用いたデータの分析業務、それらの結果に基づいた顧客への提案をしております^[1]。所属チームでXを運用しており、AIに関する情報を発信していますのでご興味あれば覗いてみてください。

本記事では、統計的仮説検定の考え方を基本から確認していき、検定の計算過程を辿ることで、検定の最強力性を理解したり、p値に対する誤解を解いたりしながら、一度は抱いたであろう統計的仮説検定に対する種々の疑問を解消します。より真摯なデータ分析への足掛かりにするだけではなく、統計の考え方・面白さを存分に味わうことを目指します。

また、記事の分量が多くなってしまったので、できるだけつまみ読み^[2]できるように書いた都合上、冗長な記事になっているかもしれません。その点ご了承ください。

想定読者として、統計的仮説検定の教科書的な説明を読んだことがあるだけの方にも理解しやすいように心がけて書いたつもりですが、難しい場合は3章: 統計的仮説検定を飛ばして読むことをおすすめいたします。

統計的仮説検定の目的

まずは統計的仮説検定（以後、単に「検定」と表記します）が何を目指しているのか、具体例から見ていきましょう。

紅茶の違いがわかる婦人

1920年代、場所はケンブリッジのある夏の午後、大学教授らとその夫人などからなるグループが、アフタヌーンティーを楽しんでいました。その中のある婦人がこう言いました。

紅茶にミルクを注ぐのと、ミルクに紅茶を注ぐのでは味が違うのよ

これに対して、灰色のヴァンダイク髭^[3]の男^[4]が、「検定してみよう！」と言ったそうです。彼とそのグループは議論を重ね、紅茶にミルクを注いだり、ミルクに紅茶を注いだりしたカップをたくさん用意し、

• 用意するカップの数
• 出す順序
• どの程度まで実験に関する情報を婦人に伝えるか

等を取り決め^[5]、淹れ方の異なるカップを次々と婦人に差し出しては、婦人の回答結果をメモしていきました。

統計的仮説検定の目指すところ

検定の目指すところは、婦人が、「紅茶にミルクを注いだカップと、ミルクに紅茶を注いだカップを区別する能力があるかないか」を知ることです。カップの区別の場合、能力がない人であっても出鱈目に言えば1/2の確率で言い当てることができるので、1つのカップに対して正しく言い当てることができたとしても、その人にカップを区別する能力があるとは言い切れません。では、どの程度の回数を試行し、どの程度言い当てることができれば、能力があると見做せるのでしょうか。検定の考えに基づいて考えていきます。

まず、婦人に紅茶を利き分ける能力が全くないと考えます。すると、婦人は紅茶にミルクを注いだのか、ミルクに紅茶を注いだのかを確率1/2でしか当てることができないと仮定することになります（後述する帰無仮説）。さらに、各試行が独立とみなして成功回数の分布は二項分布に従うと仮定すれば、$k$回正しく区別できる確率は以下の式で計算できます。

$$P(k) = \binom{10}{k} \left(\frac{1}{2}\right)^{10}$$

ここで、$\binom{10}{k}$ は組み合わせを意味します。カップを区別する試行を10回行い、それぞれの試行で正しく言い当てられる（成功）確率が1/2の場合、$k$回成功する確率は以下の通りです。

成功回数$k$	発生確率
0	0.0009765625
1	0.009765625
2	0.0439453125
3	0.1171875
4	0.205078125
5	0.24609375
6	0.205078125
7	0.1171875
8	0.0439453125
9	0.009765625
10	0.0009765625

例えば完全な実験計画のもとで、カップを区別する能力のない婦人が10個のカップに対して8つのカップを正確に言い当てられたとすると^[6]、0.0439453125 + 0.009765625 + 0.0009765625 = 0.0546875くらいの確率^[7]でしか起きないことだと考えます。他の仮定が全て正しいとすると、婦人に能力がないという仮定とこの低確率な事象は矛盾するので、実験設定と仮定に矛盾があったり、婦人には能力があるのではないか^[8]、と考えます。ただし、本当に婦人にはそんな能力がないとしても、0.0546875くらいの確率で8つ以上のカップを出鱈目に言い当てることができてしまいます。そこで、誤った判断をしてしまうリスクを小さくする意義で、この値が0.1や0.05以下じゃないと信頼できないですよね、これくらいのリスクなら許容できますよね、という風に、恣意的に決めた基準（有意水準）以下かどうかを確認します。

このように、ある関心のある仮説（命題）が正しいか否かをデータから判定する統計手法を統計的仮説検定と呼びます。

本記事の後段で詳しく説明しますが、この0.0546875という数字はp値と呼ばれるものに相当します。この計算過程をじっくり見ると、p値は決して帰無仮説が正しい確率でもなければ、婦人にカップを区別する能力がないとしたときに、誤って能力があると判断してしまう確率でもありません。このような確率的矛盾は、婦人の能力以外にも起因する可能性があり、それらの総合的な矛盾度を表していると考えます。確率的矛盾を生じさせる例として、以下の事柄が挙げられます。

• カップの混ぜ方が足りなかったり、ミルクの賞味期限が切れていたりして婦人が能力を十分に発揮できなかった（実験の不備）
• 婦人は、「ミルクに紅茶を注ぐ」と予想する傾向が強く、カップを差し出す方も「ミルクに紅茶を注ぐ」方をたくさん用意する傾向があった（帰無仮説の設定）
• 婦人は一度間違えると落ち込んでしまい、次のカップを当てる精度が下がってしまう（統計モデルとの矛盾）

このように、婦人の能力という帰無仮説以外の、統計モデルと実態との乖離度合いによってもp値は大きくなったり小さくなったりします。従って、小さいp値が得られれば婦人には利き紅茶をする能力があると即決できるわけではないのです。上記のような後付け設定を持ち出すのはずるい、といいたくなるかもしれませんが、現実世界の複雑な実験ではそうはまいりません。このようなp値にまつわる誤解について、明確に何故誤解なのかを知ることも本記事のゴールの1つです。

統計的仮説検定の落とし穴

前節で、統計的仮説検定を以下のように説明しました。

このように、ある関心のある仮説（命題）が正しいか否かをデータから判定する統計手法を統計的仮説検定と呼びます。

ここには有名な落とし穴がありまして、基本的に検定だけでは仮説が正しいかどうかを一発で判定は不可能です。各用語の説明はしていませんが、ここでもう1つ例を見てみましょう。

あるイベントの集客を増やすための検討中施策が100種あります。施策を成功させることは難しく、この100種類の中で有効な施策は10種類しかないとします。もちろん、どの10種類が有効な施策かはわからないので、これから実験して、いつもやっている施策と比べて有意水準$\alpha=0.05$、検出力$\beta=0.8$の検定で有意な施策を調べていきます。

検出力は0.8なので、実際に効果のある施策10種のうち、8種は帰無仮説を棄却してくれます（2種類は残念ながら第2種の誤りとして帰無仮説を棄却できません）。そして、有意水準は0.05なので、残りの効果のない施策90種のうち、$90 \times 0.05 = 4.5$種が第1種の誤りとして帰無仮説を棄却してしまいます。よって、帰無仮説を棄却した8+4.5=12.5種類^[9]の施策が「有意な施策」のように見えます。ではこの実験結果を以って来年度の施策を行いましょう（意思決定）。するとどうですか？12.5回施策を打っても、8回しか実際に意味のある施策にはなりません。割合でいうと64%です。一度しっかり有意水準が5%の実験をしているにも関わらず、36%も無意味な施策にお金と人的リソースを割くことになります。もっといえば、良い施策だけやっていれば得られたはずの利益までも失ってしまうのです（逸失利益）。もし顧客に「有意水準5%で実験しましたので、95%の施策は当たりますよ！」なんて言っていたらと思うと背筋が寒くなります。

種明かしをします。ベイズの定理を学んだときの練習問題として病気の検診と罹患の割合を計算した人にとってはどこか聞いたことのある話のように感じたかと思います。今回の調査では、基準率^[10]と呼ばれる、調査対象の中にある興味の対象の割合を考慮していませんでした。基準率は非常に重要で、これが低い場合には有意水準が0.05であろうと0.001であろうと、偶然による産物である可能性が高くなってしまいます。このように、p値の低さと施策の有効性の信頼度は別物です。

次の章からは統計的仮説検定の理論、その次の章からは本節でも紹介したp値にまつわる話題を掘り下げていきます。

統計的仮説検定

本章では、検定の復習を簡単に行い、私が今まで感じた検定に関する素朴な疑問の私なりの回答を示し、検定への理解を深めます。また、今まで何気なく使っていた検定手法は尤度比検定と一致することを確認しそれらが「良い検定手法」であることを味わいます。

検定の枠組み

検定の枠組みでは、帰無仮説$H_0$（null hypothesis）と対立仮説$H_1$（alternative hypothesis）という2つの排反^[11]な仮説を設定します。ここで設定する仮説は、母集団の分布や母集団のパラメータに関する記述であり、以後母集団の確率密度関数を$f(x;\theta)$、帰無仮説における母集団のパラメータを$\Theta_0$、対立仮説における母集団のパラメータを$\Theta_1$とします。こうすることで、$\theta \in \Theta_0$か、$\theta \in \Theta_1$（排反なので$\Theta_0 \cap \Theta_1 = \emptyset$^[12]）のどちらかを判定する問題として扱うことができます。これを以下のように書きます。

$$H_0: \theta \in \Theta_0 \quad \text{vs} \quad H_1: \theta \in \Theta_1$$

そして、仮説を否定することを、棄却する（reject）と言い、仮説を受け入れることを受容する（accept）と言います。ご存知の方も多いでしょうが、否定したい仮説を帰無仮説にし、有意水準$\alpha$を事前に設定し、そこから計算を進めて背理法的に確率的な矛盾を導くことで、帰無仮説が怪しい（帰無仮説を棄却）のではないかという主張を行います。この時、確率的矛盾が生じているかどうかを、帰無仮説をもとに計算して得られるある値$T(X)$（検定統計量）と、ある閾値$C$を比較することによって判断します。これが教科書的な検定の説明です。

帰無仮説と対立仮説はどのように設定する？

仮説は$\theta \in \Theta_0$のような表記をしているように、調べたいパラメータの集合ですが、集合の要素が1つである仮説を単純仮説といいます。一方、$\theta \neq \theta_0$や$\theta \leq \theta_0$のように複数の点からなる仮説を複合仮説と呼びます。帰無仮説が単純仮説なら、当然その値を用いて計算を進め、検定統計量$T(X)$を求めて、閾値$C$と比較できます。そして複合仮説の場合であっても、それら複数の仮説の中での上限（sup）を考えることで、計算が可能です（ある値$C$を閾値として棄却すると決めたのであれば、それよりも極端な結果である$C+1$のような値も棄却するというのは自然な考えだからです）。有意水準$\alpha=0.05$、婦人が紅茶を正しく区別できる確率を$\theta$（ベルヌーイ分布のパラメータ）とします。例えば、$H_0: \theta \leq 1/2$という帰無仮説であれば、検定で実現したいことは有意水準で抑えることなので以下の不等式を成立させなければなりません。

$$\text{帰無仮説における独立なベルヌーイ試行を10回繰り返して、X回以上成功する確率} < \alpha$$

これは、左辺（「帰無仮説における独立なベルヌーイ試行を10回繰り返して^[13]、X回以上成功する確率」）の$\theta \leq 1/2$において上限をとる$\theta=1/2$について成立していれば残りの$\theta$では全て成立するので、$\theta = 1/2$として計算して得られた確率が$\alpha$よりも小さいことを以って、$H_0$全てに対して成立したと言えます（$\theta=1/2$が成立していれば、より確率の小さくなる$\theta=1/3$も成立しますよね）。

上記の上限（sup）の考え方が基本的には使えるので、帰無仮説・対立仮説はどちらも単純仮説でも複合仮説でも問題ありません。そして、以降の説明では帰無仮説のsupを用いて計算することは断りなく用います。

何故帰無仮説を棄却？

次のような疑問を抱いたことのある方は多いのではないでしょうか。

何故、わざわざ回りくどく帰無仮説を棄却することを以って、立証したい事柄を統計的に正しいかのように主張するのでしょうか。

この問いに対する私なりの回答は、「帰無仮説を棄却することを以って、立証したい事柄を統計的に正しいかのように主張する」こと自体が誤りです。そして、「ある事象が矛盾しないことを以ってその事象が正しい」とは言えない為^[14]、せめてデータや統計モデルの矛盾を作ることで信頼度を高めようとしています（Bであると積極的に主張することは難しいですが、Aと考えるとどこかに矛盾が起きる、程度の主張ならできます）。

帰無仮説をおかずに信頼区間のみを考えれば、直接的な主張ができると考えたことがある方もいらっしゃるかと思います（点推定値の値が大きくて、信頼区間が狭ければ強いことが主張できるという考え方です）。しかし信頼区間と検定は表裏一体であり、これらの差異は考える順序の違いです。信頼区間の定義は端折りますが、信頼係数$1-\alpha$の信頼区間を構成したとします。このとき以下の動画のように、

• 帰無仮説を-20としたとき、-19としたとき、、、、を小さい値から順に検定していくと、有意になる区間→有意にならない区間→有意になる区間という風に構成される
• 帰無仮説が棄却される区間は、データから推定した結果との矛盾度が大きいので、真の値が含まれていなさそうと考える
• これをずっと見ていって、矛盾しているとは言えない（＝有意ではない）区間の集合が信頼区間

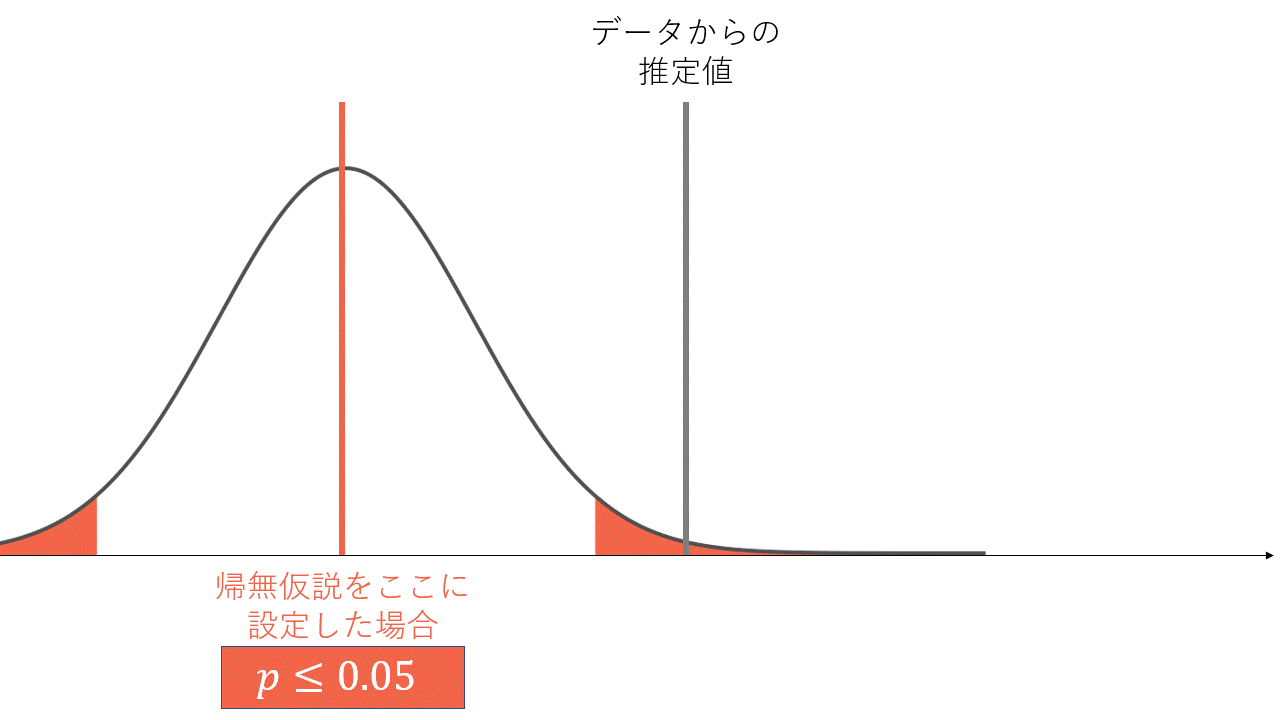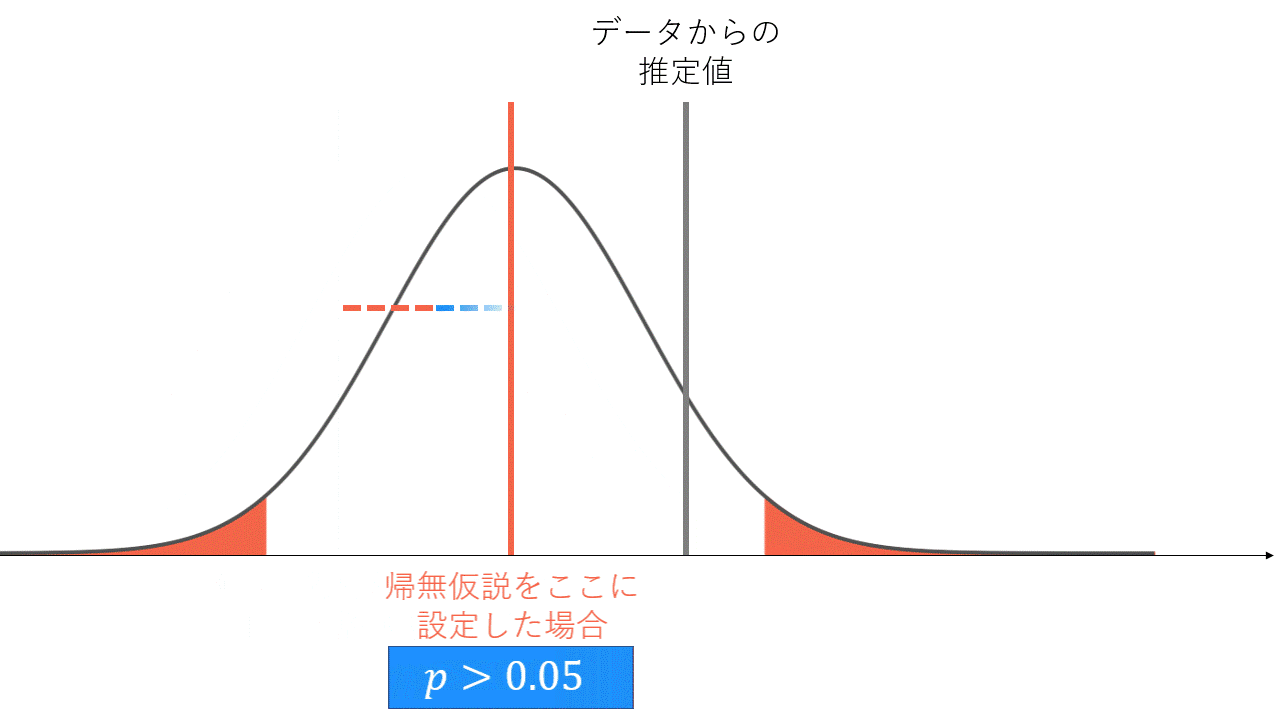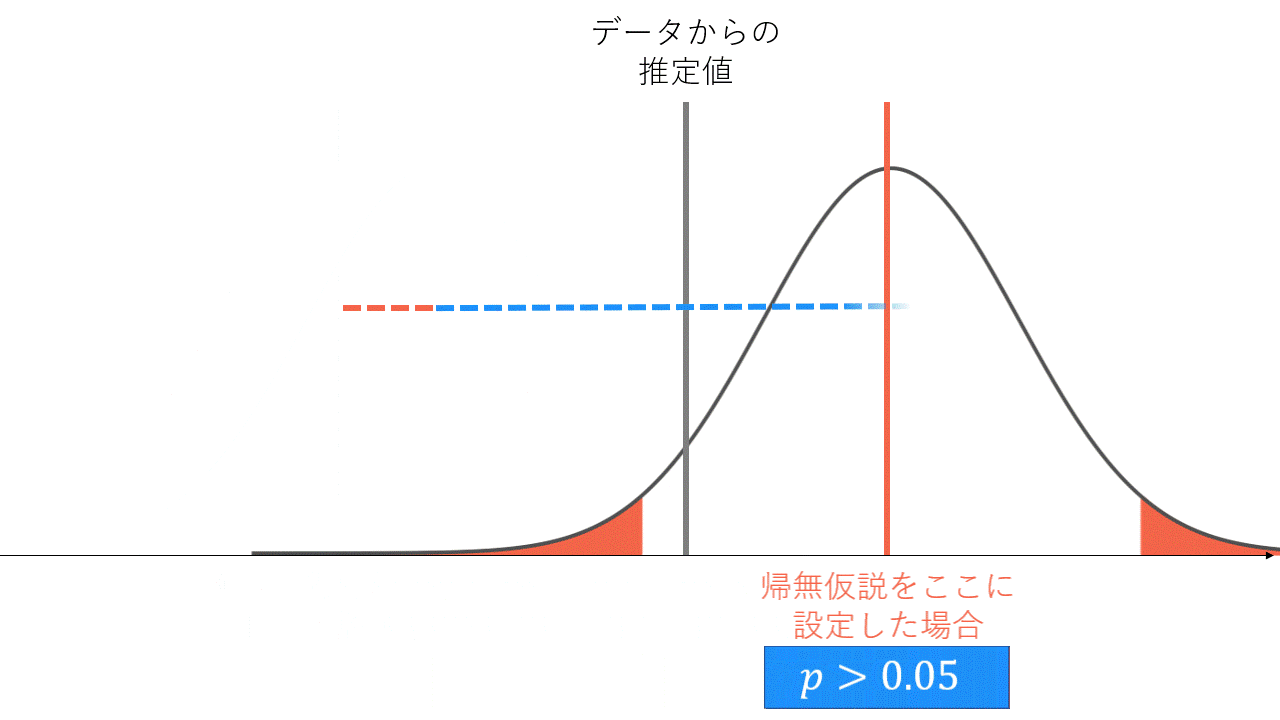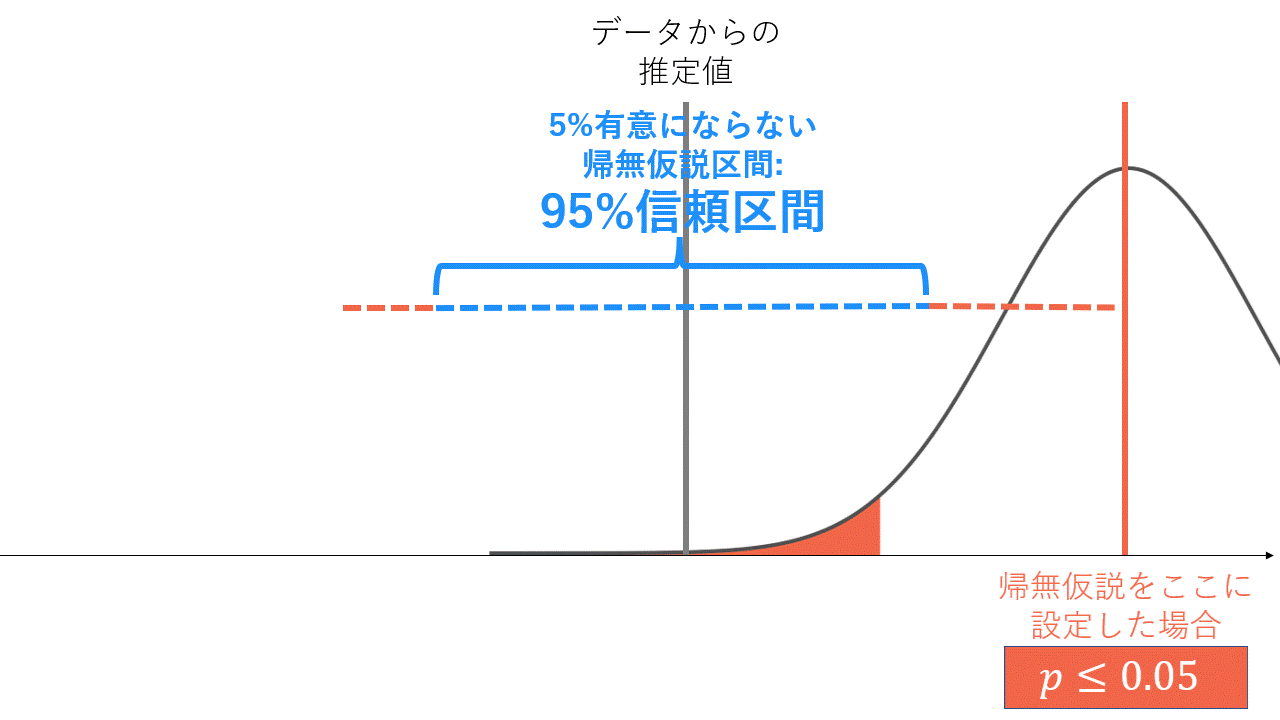
95%信頼区間と両側5%検定の関係性。正規分布の赤く塗っている箇所は両側5%区間です。

帰無仮説をある値$\psi$に設定して両側5％検定を行うことと、データから95％信頼区間を構成して、その区間が$\psi$を跨ぐかどうかは同値^[15]です。したがって、帰無仮説を立てる手順を踏むことは、ある仮説パラメータ集合上の1点について信頼区間のどのあたりに位置しているのかを調べているに過ぎません。一方、信頼区間を求めることは、ある1つの有意水準において有意にならない区間を調べているに過ぎず、両者は何を固定して何を計算しているかが異なるだけで本質は同じなのです。検定では、「効果があるのかどうか」を調べたいときに用いるツールという位置付けですので、効果がないという仮説パラメータ集合に対する矛盾度を計算することは自然な発想です。繰り返しにはなりますが、もし逆に「効果がある」ことを元に計算を進めて、「確率的に起きても全然おかしくない」という結果が得られたとしても、信頼性のある論証には全くなりません^[16]。

検定の例

ここで一旦、有名な検定手法を眺めてみましょう。いずれも統計の教科書には必ず書いてある重要な検定手法ですので、ご存知の方は読み飛ばしてください^[17]。

検定の例①: 分散の比較

2つの母集団があり、それぞれの分散が等しいか否かを検定します。$X_1, \ldots , X_n, \text{i.i.d.} \sim N(\mu_1, \sigma_1^2)$、$Y_1, \ldots , Y_m, \text{i.i.d.} \sim N(\mu_2, \sigma_2^2)$として、以下のように帰無仮説と対立仮説を設定します。

$$H_0: \sigma_1^2 = \sigma_2^2 \quad \text{vs} \quad H_1: \sigma_1^2 \neq \sigma_2^2$$

$\sigma_1^2$と$\sigma_2^2$はそれぞれ、$\hat{\sigma_1^2}=\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2, \hat{\sigma_2^2}=\frac{1}{m-1}\sum_{i=1}^{m}(y_i - \bar{y})^2$で不偏推定でき、それらの比$\hat{\sigma_1^2}/\hat{\sigma_2^2}$が検定統計量となります。こうすると、帰無仮説$H_0$のもとでは、$\sigma_1^2=\sigma_2^2$であり、これを$\sigma^2$とすると、

$$\frac{\hat{\sigma_1^2}}{\hat{\sigma_2^2}} = \frac{\hat{\sigma_1^2}/\sigma^2}{\hat{\sigma_2^2}/\sigma^2} \sim F_{n-1, m-1}$$

となり、自由度$(n-1, m-1)$のF分布から棄却域を作れます。

検定の例②: 平均値の比較

確率変数$X_1, \ldots , X_n$が互いに独立に平均$\mu$, 分散$\sigma^2$の正規分布に従うとします（$X_1, \ldots , X_n \text{i.i.d.} \sim N(\mu, \sigma^2)$）。$\sigma^2$は未知とします。平均$\mu$が$\mu_0$かどうかを検定するには、以下の両側検定を構成します。

$$H_0: \mu = \mu_0 \quad \text{vs} \quad H_1: \mu \neq \mu_0$$

そして、帰無仮説$H_0$のもとで、標本平均$\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i$と、不偏分散$s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2$を用いて、検定統計量$T$は

$$T = \frac{\bar{x}-\mu_0}{\sqrt{\frac{s^2}{n}}} \sim t(n-1)$$

となります（自由度$(n-1)$のT分布に従います）^[18]。よって、$|T| \leq t_{\alpha/2}(n-1)$となれば、帰無仮説を棄却できます。ただし、$t_{\alpha/2}(n-1)$は自由度$(n-1)$のT分布の上側$100\alpha/2\%$点です。

良い検定とは？

さて、ここで疑問です。

分散の検定では比率を計算してF分布、平均の検定では差を計算してT分布から確率を計算しました。仮に平均値を用いずに中央値を用いて閾値を判断しても良いですし、分散の検定では比率ではなく差が従う分布を頑張って考えることもできるかもしれません。このように、他にもいろいろな検定方法が考えられますが、何故決まりきった検定方法が用いられ続けられているのでしょうか。

本節からは検定の良し悪しについて議論していきます。

検定手法というものは、帰無仮説の棄却域の決め方と同等であり、棄却域の取り方は検定統計量を変えるなどして上記の問題提起のように無数に考えることができます。そこで、複数の検定手法の優劣を決める方法を考えていきたいです。これを考えることができれば、上記の質問にもズバッと、「XXという観点で見たときに、最も良い検定方法だからです！」と答えられるようになります。

検定における2種類のエラーと検定の評価

検定には2種類のエラーがあります。それは、帰無仮説が正しいのに帰無仮説を棄却してしまうエラーと（第1種の誤り）、対立仮説が正しいのに、帰無仮説を受容してしまうエラーのことです（第2種の誤り）^[19]。

（一様）最強力検定

この2種類のエラー（第1種の誤り、第2種の誤り）はトレードオフの関係にあり、棄却限界値をどのように動かしても、両方のエラーを同時に改善させることはできません。この様子は以下の図の通りです。

第1種の誤りと第2種の誤りはトレードオフの関係。棄却域をどのように動かしても、両者の誤り率を同時に改善させることはできません。

このような場合、機械学習のクラス分類問題の precision vs recall において調和平均を取るように、何らかのバランスをとる方法も考えたくなるかもしれませんが、慣習的に検定ではまず有意水準$\alpha$を定めることで第1種の誤り発生確率を一定以下に抑えた後、第2種の誤り発生確率をできるだけ小さくするという方法が用いられます^[20]。このような、ある有意水準$\alpha$の検定の中で、最も検出力が高い検定を一様最強力検定といいます。「強力」というのは、同じ有意水準において検出力が強いことを、「一様」というのは複合仮説におけるどんな対立仮説においても最も強力であることを意味します。すなわち、良い検定というのは第1種の誤り発生確率を$\alpha$以下に抑えた後、検出力をできるだけ大きくするような検定と考えられています。ただし、一様最強力検定は必ずしも存在するとは限らないのです。

ネイマン・ピアソンの補題と尤度比検定

ネイマン・ピアソンの補題（Neyman-Pearson lemma）とは、帰無仮説も対立仮説も両方が単純仮説であれば、その特定の対立仮説の中で最も強力な検定（最強力検定^[21]）は尤度比検定であるという主張です。次のような検定を考えてみます。

$$H_0: \theta = \theta_0 \quad \text{vs} \quad H_1: \theta = \theta_1$$

$X$の確率密度関数を$f(X;\theta)$としたとき、尤度の比$L'$は以下のように表されます。

$$L' = \frac{f(X;\theta=\theta_1)}{f(X;\theta=\theta_0)}$$

かなり強引に端折ってしまいますが^[22]、単純仮説でないときでも、尤度の十分統計量に関する部分が単調尤度比を持つ場合、片側検定については一様最強力検定になります。また、検定の種類を不偏検定に絞ることで両側検定についても一様最強力検定にできます。こういった議論から、単純仮説に絞らない以下の一般の検定を再度考えた時、

$$H_0: \theta \in \Theta_0 \quad \text{vs} \quad H_1: \theta \in \Theta_1$$

新たに以下の尤度比を考えます。

$$L = \frac{\text{sup}_{\theta \in \Theta_1} f(X|\theta)}{\text{sup}_{\theta \in \Theta_0} f(X|\theta)}$$

どちらを分子に持っていっても良いのですが、本記事では対立仮説の方を分子に持ってきているので、対立仮説の方が尤度が一定以上高いとき、すなわち、$L > c$のときに帰無仮説を棄却する検定を構成します（これを尤度比検定といいます）。直感的には、「帰無仮説のもと」と「対立仮説のもと」での起こりやすさの比を見ているので、それっぽい指標になっています。

尤度比検定との一致を確認する

天下り的^[23]ではありますが、尤度比検定を受け入れて有名な検定手法を導出してみましょう。

分散の比の検定

等分散性の検定を尤度比検定で書いてみます。確率変数$X,Y$はそれぞれ$X \sim N(\mu_1, \sigma_{1}^2), \quad Y \sim N(\mu_2, \sigma_{2}^2)$とします。それぞれの分布から$n$個の標本$X_1, X_2, \cdots, X_n, Y_1, Y_2, \cdots, Y_n$をサンプリングしたとして、次の検定を考えます。

$$H_0: \sigma_1^2 = \sigma_2^2 \quad \text{vs} \quad H_1: \sigma_1^2 \neq \sigma_2^2$$

得られたデータの尤度$f(X,Y|\mu_1, \mu_2, \sigma_{1}^2, \sigma_{2}^2)$は確率密度関数を掛け続ければ良いので以下のように書けます。

$$f(X, Y|\mu_1, \mu_2, \sigma_{1}^2, \sigma_{2}^2) = \frac{1}{\sqrt{2 \pi \sigma_{1}^2}^{n}} \exp(-\frac{1}{2 \sigma_{1}^2} \sum_{i=1}^{n}(x_i - \mu_1)^2) \\ \times \frac{1}{\sqrt{2 \pi \sigma_{2}^2}^{n}} \exp(-\frac{1}{2 \sigma_{2}^2} \sum_{i=1}^{n}(y_i - \mu_2)^2)$$

上式は対立仮説における尤度を表します。帰無仮説のもとでは、$\sigma_{1}^2 = \sigma_{2}^2 = \sigma^2$とおくことで上式を、

$$f(X,Y|\mu_1, \mu_2, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}^{n}} \exp(-\frac{1}{2 \sigma^2} \sum_{i=1}^{n}(x_i - \mu_1)^2) \\ \times \frac{1}{\sqrt{2 \pi \sigma^2}^{n}} \exp(-\frac{1}{2 \sigma^2} \sum_{i=1}^{n}(y_i - \mu_2)^2)$$

と書き直せます。尤度比検定に持っていきたいので、各仮説のもとで尤度の上限（sup）を取ることを考えます。対立仮説のもとで尤度$f(X,Y|\mu_1, \mu_2, \sigma_{1}^2, \sigma_{2}^2)$を最大にするには、パラメータで偏微分してイコール0（$f(\cdot)=0$）を解けばよく、実際に計算すると以下のような見慣れた式になります。ただし推定したパラメータにはハットを被せます（$\hat{\cdot}$）。

$$\hat{\mu_1} = \frac{1}{n}\sum_{i=1}^{n}x_i, \quad \hat{\sigma_1} = \frac{1}{n}\sum_{i=1}^{n}(x_i - \hat{\mu_1})^2 \\ \hat{\mu_2} = \frac{1}{n}\sum_{i=1}^{n}y_i, \quad \hat{\sigma_2} = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{\mu_2})^2$$

これらを$f(X, Y|\mu_1, \mu_2, \sigma_{1}^2, \sigma_{2}^2)$に代入することで、尤度の上限が得られます。

$$\text{sup}_{\Theta_1}f(X,Y|\mu_1, \mu_2, \sigma_{1}^2, \sigma_{2}^2) = \frac{1}{\sqrt{2 \pi}^n} e^{-n} \frac{1}{\sqrt{\hat{\sigma_1}^2\hat{\sigma_2}^2}^n}$$

同様の計算で、帰無仮説のもとでの尤度の上限（sup）は、

$$\text{sup}_{\Theta_0}f(X,Y|\mu_1, \mu_2, \sigma^2) = \frac{1}{\sqrt{2 \pi}^n} e^{-n} \frac{1}{(\hat{\sigma}^2)^n}$$

となりますので、これらから尤度比$L$は、

$$L = \sqrt{\frac{1}{4}}^n (\frac{\hat{\sigma_2}}{\hat{\sigma_1}} + \frac{\hat{\sigma_1}}{\hat{\sigma_2}})^n$$

この尤度比$L$は比率$\frac{\hat{\sigma_2}}{\hat{\sigma_1}}$の関数となっているので^[24]、棄却域は次の形式で表すことになります。

$$\frac{\hat{\sigma_{2}^2}}{\hat{\sigma_{1}^2}} > a$$

実は、

$$\frac{\hat{\sigma_{2}^2}}{\hat{\sigma_{1}^2}} = \frac{n \hat{\sigma}_{2}^2 / (n-1)\sigma^2}{n \hat{\sigma}_{1}^2 / (n-1)\sigma^2}$$

なので、これは自由度が$(n-1,n-1)$のF分布に従います。ここまで来ればF分布から両側5%の棄却域を設定することで検定を構成できそうですね。これはどの教科書にも載っているF検定というやつです。F検定は尤度比検定から導出できる検定手法だったのです。

平均の差の検定

平均値の差の検定を尤度比検定で書いてみます。$X_1, X_2, \cdots, X_n \text{i.i.d.} \sim N(\mu, \sigma^2)$として次の検定を考えます。

$$H_0 : \mu = \mu_0 \quad \text{vs} \quad H_1 : \mu \neq \mu_0$$

尤度は、

$$f(X|\mu, \sigma^2) = \prod_{i=1}^{n} f(x_i; \mu, \sigma^2) = \left( \frac{1}{\sqrt{2\pi\sigma^2}} \right)^n \exp \left( -\frac{1}{2\sigma^2} \sum_{i=1}^{n} (x_i - \mu)^2 \right)$$

となります。$H_0$のもとで$\sup_{\sigma^2} f(X|\mu_0, \sigma^2)$^[25]となる$\hat{\sigma}_0^2$は$\hat{\sigma}_0^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \mu_0)^2$ですので、上限は以下の通りです。

$$\sup_{\sigma^2} f(X|\mu_0, \sigma^2) = \left( \frac{1}{\sqrt{2\pi \hat{\sigma}_0}^2} \right)^n \exp \left( -\frac{n}{2} \right)$$

一方、$H_1$のもとで$\sup_{\mu, \sigma^2} f(X|\mu, \sigma^2)$は

$$\hat{\mu}_1 = \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \\ \hat{\sigma}_1^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2$$

ですので、尤度比検定の棄却域は

$$\begin{align*} \frac{\sup_{\mu, \sigma^2} f(x| \mu, \sigma^2)}{\sup_{\sigma^2} f(x| \mu_0, \sigma^2)} &= \frac{\left( \frac{1}{\sqrt{2\pi \hat{\sigma_1}^2}} \right)^n \exp\left[ -\frac{n}{2} \right]}{\left( \frac{1}{\sqrt{2\pi \hat{\sigma_0}^2}} \right)^n \exp\left[ -\frac{n}{2} \right]} \\ &= \frac{\left( \frac{1}{\sqrt{\hat{\sigma}_1^2}} \right)^n}{\left( \frac{1}{\sqrt{\hat{\sigma}_0^2}} \right)^n} \\ &= \left( \frac{\hat{\sigma}_0^2}{\hat{\sigma}_1^2} \right)^{n/2} \\ &= \left( \frac{\sum_{i=1}^{n} (x_i - \mu_0)^2}{\sum_{i=1}^{n} (x_i - \bar{x})^2} \right)^{n/2} \\ &= \left( 1 + \frac{n (\bar{x} - \mu_0)^2}{\sum_{i=1}^{n} (x_i - \bar{x})^2} \right)^{\frac{n}{2}} \\ &\geq c \end{align*}$$

ここで、

$$t = \frac{\bar{x} - \mu_0}{\sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n}}} \sim t(n-1)$$

とおくと、

$$\left( 1 + \frac{n (\bar{x} - \mu_0)^2}{\sum_{i=1}^{n} (x_i - \bar{x})^2} \right)^{\frac{n}{2}} \geq c \\ \ \\ \Longleftrightarrow (1+t^2)^{\frac{n}{2}} \geq c$$

とまで変形できます。最後の左辺は$t$に関して単調増加関数ですので、新たな棄却限界値$c'$を設定すれば、棄却域は$|t| \geq c'$と書けます。こちらも尤度比検定から着地できました。

一般の検定

先の2つの例では尤度比検定から棄却域を設定できましたが、一般的には棄却域の設定が困難な場合が多いです。データ数が多くなると、尤度比は以下のように漸近近似ができますので、これを用いて検定を構成（棄却域が$\alpha$となる区間を設定）できます。

$$2\log{L} \rightarrow \chi^2(p)$$

p値をめぐる誤解の数々

統計的仮説検定を語る上で、p値の話に触れないわけにはまいりません。ここまでにも触れてきたように、p値は非常に誤解されやすい概念です。しかし、数々の前振りと検定の導出まで見てきた我々であれば、p値を正しく解釈できるはずです。

本章はASA声明^[26]に準拠します。ASA声明は短い文章でp値に関する原則について説明されています。和訳や、多数の解説記事から情報を得ることはでき、ふむふむと読み進めることができるので、是非原文か、和訳を読んでみてください。和訳も出されている8年も前の声明文を本記事であえて紹介しているのは、検定の導出過程と照らし合わせながら「味わう」ためです。

併せて、以下のYouTube動画を視聴すると一層p値への理解が深まると思います。

https://www.youtube.com/watch?v=vz9cZnB1d1c

p値の意味

ASA声明（の和訳）によると、「p値をざっくり言うと」は以下のとおりです。

特定の統計モデルのもとで検定統計量が観察された値、もしくはそれより極端な値をとる確率

そして、p値の解釈は次のとおりです。

P 値はデータと特定の統計モデル（訳注:仮説も統計モデルの要素のひとつ）が矛盾する程度をしめす指標のひとつである。

ここで重要なことは、検定というものは、帰無仮説以外にも多くの仮定に基づいて計算されているということであり、p値の低さは、それら帰無仮説以外の仮定が間違っている可能性も考慮しなければならないということです。ここでいう帰無仮説と、帰無仮説以外の仮定とは、例えば以下のような事柄が挙げられます。

• データが正規分布している
• 平均値が等しい（帰無仮説）
• 実験計画法が守られている
  • ランダム化
  • サンプリング
  • 割り付け

低いp値が得られた時、これらの仮定のうち1つ以上が矛盾していることを意味し、帰無仮説が矛盾しているのかそれ以外が矛盾しているのかを区別できません。

本来は帰無仮説以外全て正しくできているなら、帰無仮説だけが怪しいという風に考えたいのですが、帰無仮説以外が全て正しいかどうかを確実に立証することは不可能なので、p値はあくまでも目安にしかすぎないということです。この考え方と、前章までの検定の導出過程をもとに、次節からのp値に関する誤解や原則を確認していきます。

よくある誤解

私がインターネット上などで見聞きした代表的なp値に対する誤解は以下の3つに要約されます。

1. p値は帰無仮説が正しい確率である
2. p値により有意かどうかを判定し、その結果に応じて帰無仮説を採択/棄却する
3. p値が0.05ということは、100回に5回しか起こらないことが起こったことを意味し、帰無仮説を棄却しても100回に5回の確率（5%）しか間違わない

では、1つずつ何故誤解かを確認していきます。

1. p値は帰無仮説が正しい確率である

この誤解は、本記事を上から順に読んでいれば明らかな間違いだと気づけるはずです。p値は帰無仮説が正しいと仮定して計算を進めて算出した統計量がより極端になる確率でしたよね。例えばp値が0.6とかで全然有意ではないとき、帰無仮説が正しい確率が60％ですって言われたら違和感しかなくないですか？もし納得がいかない場合には本記事の序盤に挙げた例をもう一度読み返して、やはりこれが誤解であることを噛み締めてください。

2. p値により有意かどうかを判定し、その結果に応じて帰無仮説を採択/棄却する

まずは

有意ではない検定結果が得られれば、帰無仮説を採択する

を考えます。有意ではない結果は、仮説とデータがそんなに矛盾しなかったことを表しているに過ぎず、矛盾がないから仮説が正しいと考えるのは早計だと思える人は多いと思います。

一方、次の誤解を見た時に、驚く方も多いかもしれません。

有意な検定結果は帰無仮説が誤りであり、棄却する

言葉の定義の問題ですが、「棄却する=p値が有意水準を下回っている」という意味であれば正しいのですが、「棄却する=帰無仮説が誤りであると判断する」という意味であれば誤解です。本記事のp値の意味でも述べたように、あくまでもp値はデータと統計モデルの矛盾する程度を示す指標であり、データが矛盾している（帰無仮説がおかしい）のか、統計モデルが矛盾している（実験設定やモデルの仮定がおかしい）のかを区別する能力はないので、p値のみでは直ちに帰無仮説が誤りだと断定することはできません。繰り返しになりますが、有意水準が5％だから第1種の誤りがあるからという意味ではなく、他の仮説も疑うべきだという話です。実際、尤度比を用いた検定の導出過程では、データが無作為化されていることや、データが独立に正規分布している^[27]ことなどが前提として計算していました。以下は尤度の計算式の再掲です。

$$f(X, Y|\mu_1, \mu_2, \sigma_{1}^2, \sigma_{2}^2) = \frac{1}{\sqrt{2 \pi \sigma_{1}^2}^{n}} \exp(-\frac{1}{2 \sigma_{1}^2} \sum_{i=1}^{n}(x_i - \mu_1)^2) \\ \times \frac{1}{\sqrt{2 \pi \sigma_{2}^2}^{n}} \exp(-\frac{1}{2 \sigma_{2}^2} \sum_{i=1}^{n}(y_i - \mu_2)^2)$$

偏ったサンプリングを行ったり、データが独立ではなかったりするなど（例えば）この計算が成り立たないような実験によって取得されたデータであれば、仮に本当に帰無仮説が正しいときにでも「有意な」p値が得られることになってしまいます。そして、現実世界の分析では統計の教科書に書いてあるような理想的な実験設定にはなっていません。

3. p値が0.05ということは、100回に5回しか起こらないことが起こったことを意味し、帰無仮説を棄却しても100回に5回の確率（5％）しか間違わない

本記事の序盤で示した100種の施策の例だけで十分な反例ですが、そもそも帰無仮説とはパラメータの集合なので、「帰無仮説が正しい確率」というものは存在しません。あくまでも、p値は「特定の統計モデルのもとで検定統計量が観察された値、もしくはそれより極端な値をとる確率」に過ぎず、これを明確に区別できなければなりません。

p値の原則

今度は日本計量生物学会が出したASA声明の和訳に書かれているp値に関する6つの原則を本記事での解説に合わせて簡単に紹介します（身も蓋もありませんが、私の説明よりも和訳を直接読んだ方が良いです）。

原則1: p値はデータと特定の統計モデル（訳注:仮説も統計モデルの要素のひとつ）が矛盾する程度をしめす指標のひとつである。

p値の計算過程では、帰無仮説だけではなく、データが得られる確率分布や、データが偏らずにランダム化されて得られていることなどが当然のように仮定されています。例えば紅茶の婦人の例では、婦人が紅茶を利き分ける能力が1/2であったとしても、仮定が満たされていなければ他の要因で正答率が8/10になるような状況も考えられます。このように、p値は帰無仮説だけではなく、モデル全体がどれほど矛盾しているかを総合した指標であり、どの要素が矛盾しているかを区別する能力がないということが特徴です。

原則2: p値は、調べている仮説が正しい確率や、データが偶然のみでえられた確率を測るものではない。

p値が帰無仮説が正しい確率ではないことはもう十分にわかっているかと思います。また、p値は帰無仮説だけではなく、たくさんの仮定を元に算出しており、仮説や仮定の確率を直接示すものではありません。後半の「データが偶然のみで得られた」という部分は、むしろ仮定の1つです。この仮定に従って尤度を計算していたのに、p値が「データが偶然のみで得られた確率」と考えるのは無理があります。

原則3: 科学的な結論や、ビジネス、政策における決定は、p値がある値（訳注: 有意水準）を超えたかどうかにのみ基づくべきではない。

これについては、次節のp値と意思決定を分けるで詳説します。

原則4: 適正な推測のためには、すべてを報告する透明性が必要である。

調べた仮説のうち、有意なものだけを報告すると、報告を受る人が観測する第1種の誤り率が上昇します。これは悪意のあるチェリー・ピッキング^[28]をしていなくとも、本当は効果がないのに偶然有意な差が含まれるものを報告してしまうからです。自らの論証に有利なものだけを報告しない意図的な努力が必要です。

原則5: p値や統計的有意性は、効果の大きさや結果の重要性を意味しない。

p値が小さいとしても、効果が大きいとは限りません。T検定の式を再掲します。

$$T = \frac{\bar{X}-\mu_0}{\sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n}}} \sim t(n-1)$$

ここで効果の大きさとは、分子にある$\bar{X}-\mu_0$のことを指すと思いますが、p値は分母の$\sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n}}$にも依存するので、データのばらつき$\sum_{i=1}^{n}(x_i - \bar{x})^2$やデータの件数$n$、そしてその他統計モデルの仮定に依存しています。

また、何度も書いていますが、統計的に有意であるかどうかということは、仮定した帰無仮説や統計モデルと得られたデータの矛盾度を示しているだけなので、結果の重要性は意味しません。

原則6: p値は、それだけでは統計モデルや仮説に関するエビデンスの、よい指標とはならない。

p値の意味を思い返すと、p値単体では情報は限られています。p値以外の証拠が用意できるシーンがあれば、p値だけで論証するべきではありません。この辺りは次の節に記したp値と意思決定を分けるや再現性に関心を持つの項をご参照ください。

p値の使い方

前節の原則と、私の実務経験を通じて感じたこと、考えてきたことを元に、p値やデータ分析との向き合い方について、持論を書きます。

p値と意思決定を分ける

p値と意思決定は分けて考えなければなりません。p値が大きいからこの施策はダメだ、とか、p値が小さいからこの運用でいこう、は単純すぎます^[29]。p値がある閾値を超えているかどうかで意思決定をすることは、「分析者が想定した統計モデルと、実際得られたデータとの相性が良いかどうか」に基づいて意思決定をしているとまでは言いませんが、それに近しい状況であることは本記事を通じて身体に染み付いたところかと思います。

ついつい人間は（判断が楽になるので）p値のような1つの数字と閾値で意思決定したくなりますが、その効果の大きさや^[30]、意思決定に伴うリスクを総合的に判断する必要があります。

また、データには陽に含まれていない今年・来年特有の傾向^[31]や、他の理由で再現されることが保証される外部エビデンス^[32]も複合的に考慮する必要があり、分析者はそこまで手を伸ばして調査・報告すべきだと考えています。

大事な事は、p値がある閾値を超えるか超えないかだけで、安易に仮説を採択したり、棄却する二元論に落とし込むことはやめましょう、ということです。p値が0.06だったときに、それが人命に関わることなのか、Xのインプレッション数が変わってしまうことなのかによって扱いが大きく異なります。p値がそこそこ大きくても、効果が大きければ試す価値は大いにあるでしょう。やはり、p値だけではなく、その帰無仮説を誤って棄却/採択した時した時に被る損害の大きさによって意思決定すべきなのです。

結果を全て残す

報告バイアス^[33]などの危険があるため、学術論文では結果を全て「報告する」ことが大切ですが、ビジネスの世界ではケースバイケースだと思っています。お忙しいデータ分析チーム以外の方々に全てのデータと結果を事細かく説明するわけにもいきませんし、時間が限られた顧客と話せる時間を結果の説明だけに充てるのは勿体無いです。ただ、分析屋としては結果を全てドキュメントに「残し」ましょう。これによって、後に第三者による検証が入った時にも、当時の意思決定について再度議論できます。結果を残すなんて当たり前なことですが、当たり前なことを当たり前にできるエンジニアは優秀なエンジニアです。

再現性に関心を持つ

私は分析において最も重要と思っていることは「再現するかどうか」だと思っています。p値とか、機械学習におけるテストデータに対する精度とかいろいろやっていますけれども、それらは将来の事象に対して手元のデータから意思決定するためのツールに過ぎません。参考文献に挙げている『統計学を拓いた異才たち』から、Fisherの言葉を引用します。

生物学的方法によって生命体の研究をする際には、統計的有意性検定は不可欠である。その役割は、研究・検出しようとしている原因によってではなく、われわれがコントロールできない多くの複雑な状況から生じた偶然の出来事に惑わされないようにすることにある。もし見当をつけているものが真の原因ではないために、めったに生じ得ないという場合は、その観測結果は有意であると判断される。慣例として、偶然によって生じるのが20回の試行のうち1回未満という程度であれば、結果は有意であると判断する。研究の実務に携わっている者にとってこれは恣意的だが、便利な有意水準である。だからといって、20回に1回判断を誤るというわけではない。有意性検定は何を無視したら良いのかを教えてくれるだけにすぎない。言い換えれば、すべての実験で有意な結果が得られないということだ。かなり高い頻度で有意な結果が得られるような実験計画を知っている場合、現象は実験的に論証可能であると主張するにとどめた方がよい。そのため、再現する方法がわからない有意な結果がぽつんとあっても、これはあらためて解明されるまで未決定のままなのだ。

大切なことを言っていますが、特に、

かなり高い頻度で有意な結果が得られるような実験計画を知っている

の部分がかなり重要だと思っています。論理的に納得のいく論証ができない小さなp値は脆いです^[34]。これは報告バイアスの問題に関わってくる考えですね。

論理的に納得のいく論証ができて、それで合意できるのであれば、手元のデータで計算したp値は0.05を下回っていなくても良いのです。その意味で、私はケースバイケースでp値に頼らず、その他の数字や意思決定に至った理由を提示することで納得いただくよう努力することもあります^[35]。この時、客観的に再現しそうだと判断できるかどうかが全てで、p値はただの役立つツールの1つに過ぎないのです。

科学に真摯で謙虚な姿勢と事業への当事者意識を持つ

科学的な観点として、我々分析屋は、あくまでもp値は「特定の統計モデルのもとで検定統計量が観察された値、もしくはそれより極端な値になる割合」であり、それ以上の意味はないこのことを肝に銘じた上で、p値を上手に活用した分析をしなければなりません。そのためには、本記事の序盤で示した100種の施策の例のような、誤った印象を与えない表現を用いる工夫が必要です。

一方で、時には営業判断などで、統計的には強く言えないことを主張しなければならない板挟みも起こり得ることでしょう^[36]。顧客や営業に折れて、「私はリスクを指摘したから分析屋の仕事は終わり」とするのではなく、「では一旦その施策でやってみましょう。ただし効果検証ができるようにこんなデータをとっておきましょう。KPIはこれで、この値が〜〜」と提案するなど、できることはいろいろとあるはずです。後戻りができないほどの重大な意思決定の場合には難しいですが、保守的になり過ぎるのではなく、事業を推進するメンバーの1人として、建設的な働きかけを心がけたいと思っています。これを私は当事者意識と表現しています。

結び

統計的仮説検定の考え方を辿り、検定に関する数々の疑問を解消しながらその奥深さを味わい、最終的にはASA声明の内容を知り、「特定の統計モデルのもとで検定統計量が観察された値、もしくはそれより極端な値になる割合」と、「帰無仮説のもとで第1種の誤りが起きる確率」が別物であることに着地できたかと思います。本記事を通じて1つでも検定に関する疑問が解消されたのであれば、筆者の本望です。是非その余韻に浸ってください。

初学者にもわかりやすくなるよう一所懸命書いていたつもりでしたが、本記事の執筆を通じて自分自身が統計的仮説検定の初学者であることを再認識させられました。検定は理解が難しいところが多く、Webサイトはもちろん書籍であっても情報の信ぴょう性を丁寧に確かめながら読み進める必要があります。本記事に誤りが含まれていると思しき場合は本記事へのコメント、またはXの方にご連絡いただけますと幸いです。真摯に受け止め、修正する所存です^[37]。

参考文献

• デイヴィッド・サルツブルグ, 統計学を拓いた異才たち, 日本経済新聞出版, 2010.
• 一般社団法人 日本統計学会, 日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック, 学術図書出版社, 2020.
• 久保川達也, 現代数理統計学の基礎, 共立出版株式会社, 2017.
• Amrhein, Valentin, and Sander Greenland, Discuss practical importance of results based on interval estimates and p-value functions, not only on point estimates and null p-values, Journal of Information Technology, 2022.

お知らせ

少しでも弊社にご興味を持っていただけた方は、お気軽にご連絡頂けますと幸いです。まずはカジュアルにお話を、という形でも、副業を検討したいという形でも歓迎しています。

https://hrmos.co/pages/zenkigen/jobs?jobType=FULL
https://speakerdeck.com/zenkigenforrecruit/detailed-version-recruitment-materials-for-data-scientists

脚注

1. 執筆当時

2. 食べ物の「つまみ食い」を文字って、記事を全部読まずに気になるところだけをさらっと読むことを意味する造語です。

3. U字型の口髭とあごひげを組み合わせた髭のスタイルです。言葉の説明を読むよりも、画像検索した方がイメージしやすいです。

4. Ronald Aylmer Fisher: 統計学でお馴染みのフィッシャーのことです。

5. フィッシャーの三原則というものです。

6. 正確な書き残しはないものの、その婦人は全てのカップを正確に言い当てたという伝聞があるそうです。

7. 8回言い当てられる確率である0.0439453125だけではなく、9回言い当てられる確率と10回言い当てられる確率も足している理由は、本記事をすべて読むと完全に理解できます。

8. 帰無仮説を婦人がカップを区別できる確率が1/2としていた場合、1/2であることを疑うという意味です。

9. 施策の種類に小数点が出てしまいますが、本質的ではないので無視します。

10. 事前確率という理解で差し支えございません。

11. 一方の事象が起きたときは、他方の事象が起きない状態のことです。

12. $\emptyset$は空集合を表します。

13. 二項分布 $Bin(10, \theta$)と同じ意味です。

14. 喩えば、今まで見た鳩が全て白ければ（矛盾なし）、この世の全ての鳩が白いと言い切ってしまうのは誤りです。鯨は泳げるという点で矛盾しないので鯨を魚と分類することは誤りです。仮説に矛盾しないデータが得られたとしても、偶然かもしれませんし、2つ以上の誤りが互いに打ち消しあって矛盾していないように見えているだけかもしれませんし、とにかく「矛盾していないから正しい」は論理の飛躍があります（もちろん、運良く正しい場合もあります）。

15. 1対1に対応するくらいの意味です。

16. 同じ理屈でp値が有意水準よりも大きい時に、帰無仮説が正しいと言い切れないことは絶対にクリアしておかなければなりません。

17. というか、この記事の読者はおそらくご存知ですよね。調べなくても良いように、書き写しているくらいに思っていただければ幸いです。学生がレポートの文字数をかさ増しするようなノリでは決してございません。

18. 分散が既知であれば、それで割ることで正規分布にできますが、そんな状況は滅多にありません。直感的な理解として、データ数が少ない時には推定した不偏分散自体にも不確かさが含まれているため、その分「裾が厚い」t分布になります。

19. 第1種と第2種をどっちがどっちか覚えられない人のために、私なりの覚え方を紹介します。第1種の誤りを考える時は、帰無仮説のもとで第1種の誤りが起きる確率が$\alpha$（有意水準）と関連しています。一方、第2種の誤りを考える時は、対立仮説がしっかりと検出できるかどうかに興味があるので、検出力$\beta$と関連します。ちょうどギリシア文字の登場順と、過誤の種類番号が順になっている（1（$\alpha$）,2（$\beta$））と覚えています。

20. このような方法が用いられる背景には、検定というのは第1種の誤りを戒めるために作られたという経緯が関係しているかもしれません。仮説検定は得られたデータは全て正しいという考えを否定するために考案されたと聞いたことがあります。当時は（観測技術不足によりばらつくことはあっても）観測対象がばらつくという考えが浸透していなかった為、検定というのは偶然得られたかも知れないデータに対して過度な期待を持たないよう、戒める意味合いが強かったと言われています。

21. 対立仮説が単純仮説なので、「一様」という言葉をつけません。

22. 想定読者の範疇を超えているので、注釈も特につけません。すでにこれをしっかりと理解されている方はこの記事で学ぶことはほとんどないと思います。

23. 必要な数式や概念を、根拠を明示せずに導入してしまうことです。詳しくはgoo辞書にて

24. $\frac{\hat{\sigma_2}}{\hat{\sigma_1}} = x$とすると、尤度比は$L = \sqrt{\frac{1}{4}}^n (x + \frac{1}{x})^n$と表せます。この$x$に関する間数は$x=\frac{1}{x}=1$のときに最小値を取りますが、これは$\hat{\sigma_1} = \hat{\sigma_2}$を意味し、両者が乖離するほどこの関数値が大きくなるので、帰無仮説を検定するのにちょうど良い形になっていそうです。

25. 帰無仮説$H_0$のもとでは$\mu=\mu_0$なので、$\mu=\mu_0$は定数扱いです。

26. アメリカの統計学会が2016年に出した、統計を専門としない研究者や科学ライター向けに出された声明文です。

27. 平均値の計算にあたっては、中心極限定理が効くので、ある程度サンプルサイズが大きけばれ良いのですが、元の分布が極端に歪んでいたり、サンプルサイズが小さいと中心極限定理の効きが悪くなり、仮定が満たされなくなる場合があります。

28. 自らの論証に有利な証拠のみを選び、それと矛盾する証拠を隠す行為のことです。チェリー・ピッキングは意図的に行われることを指しますが、これを無意識に行ってしまう確証バイアスというものも存在します。

29. 脱線しますが、同様の理由で、「データ分析チャート」のようなものを個人的に嫌います。データの形式や目的だけでどの分析手法を用いれば良いかが決まるというのは便利ですが、多くの場合でケースバイケースなので、単純化されすぎているように感じます。

30. 本記事では扱っていませんが、p値とその効果の大きさは全くの別物です。効果が小さくてもデータ数が多いとp値は小さくなります。

31. わかりやすい例として、受領データの年は、「雨が少なくて凶作だった」「COVID-19の影響で人数が少なかった」ものの、来年にはおよそ回復するだろう、というような情報のことです。いわゆるドメイン知識のようなものも含まれます。

32. データ以外に仮説をサポートする理論や根拠のことです。例えば、カフェインを摂れば目が醒めるというのは覚醒度を計る実験から統計的に導き出しただけではなく、カフェインは、アデノシン受容体に結合することでアデノシン自体が結合するのを阻害するため、ヒスタミンの放出が抑制されなくなり、眠気を感じにくくなるといった、メカニズムが存在します。

33. 複数の妥当な実験研究が行われていたとしても、特定の方向に偏った結果ばかりが報告されると、報告された結果も偏ってしまうことです。

34. 家にあるサイコロを振る実験を1度行い、$p<0.05$な結果が出たとして、直ぐにサイコロメーカーを訴えますか？さらなる検証として、同じ実験を何度もやって再現するかを確かめたり、サイコロを物理的に解析して重心が大きくズレていることをエビデンスとしてもっていくはずです。どちらを選択するかはコストなどに寄りますが、一見普通に見えるサイコロに対して、1度の実験で得られた$p<0.05$は非常に脆いです。

35. 実務での具体例をここには書けないのが残念ですが、結果の再現が確認された時は、分析屋として大きな喜びを感じる瞬間の1つです。

36. 私が所属する/していた組織が云々という話ではなく、あくまでも一般論でのお話です。

37. ただし、「XXの説明を追加した方が良い」という旨のご指摘も大歓迎ですが、追加するとなると書くのが大変なので、分量が多くなるような対抗には応じられない可能性がございます。ご容赦ください。