不均衡最適輸送によるフリーハンド確率分布の評価: 確率分布間の相違度定量化手法紹介

はじめに

こんにちは。ZENKIGENデータサイエンスチーム所属のredteaです。原籍はオムロンソーシアルソリューションズ株式会社 技術創造センタですが、社外出向でZENKIGENに所属しており、数理最適化や機械学習を用いたデータの分析業務、それらの結果に基づいた顧客への提案をしております^[1]。

「はじめに」は駄文なので、技術的な内容が読みたい方はフリーハンド確率分布のスコア化からお読みください。

正規分布ってフリーハンドで描くの難しくないですか？

ここで白状しますが、私はペンを用いて字、絵、図を書いたり描いたりすることがとても苦手です^[2]。自分の結婚式に来てくれた大学時代の友人に手書きメッセージを書いた後にも、「気持ちはとても嬉しいが字は相変わらずだな」と言われたこともあります。統計の勉強をする時にはよく確率密度関数の図を手で描きますが、私の描く正規分布はもはや芸術の域に達しており、棄却域と検出力から必要なサンプルサイズを求めるには、いささか不自由を強いられてきました。とは言え、正規分布ってとりわけ描くのが難しくありませんか？変曲点が2つあることと、$x$が$-\infin$と$\infin$のときに限りなく0に近づく感じを滑らかに掴むのは特殊な訓練が必要に違いありません。

これが私が統計の勉強中に描いた正規分布です。綺麗に描く意識がないとこれくらいのクオリティに落ち着きます。X軸（横線）が真っ直ぐ引けているのは、Goodnotesの機能のおかげです。

フリーハンドの上手さを定量的に測りたい

私の図の下手さについてはこれくらいにして、他の人はどれくらい上手に描けるのか興味があります。友人や職場の同僚に描いてもらったこともありますが、「なんとなく上手そう」では納得できない性分でして、できれば上手さを定量化したいと思っています。そこで、以下のようなWebサービスをGitHub Pagesにて作成・公開しました。是非思い思いの正規分布を描いて、スコアをXなどで投稿して遊んでみてください。みなさんの正規分布を見て、いかに自分の正規分布が下手かを定量的に実感したいと思います。Xへの投稿時のハッシュタグは「#フリーハンドチャレンジ」でお願いします^[3]！

https://atsushi-green.github.io/PDF-compete/

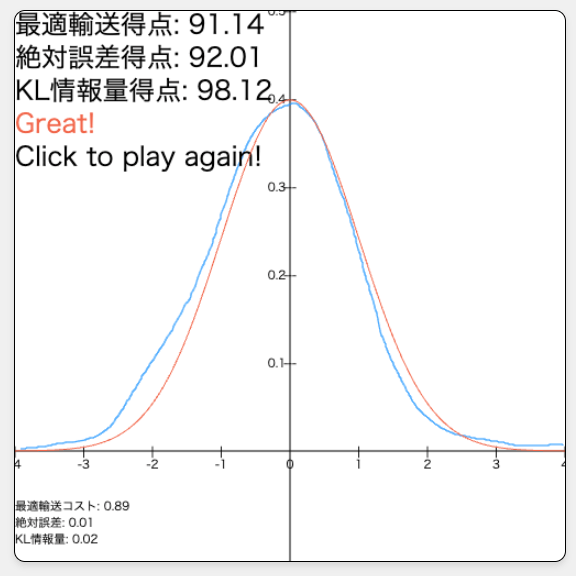
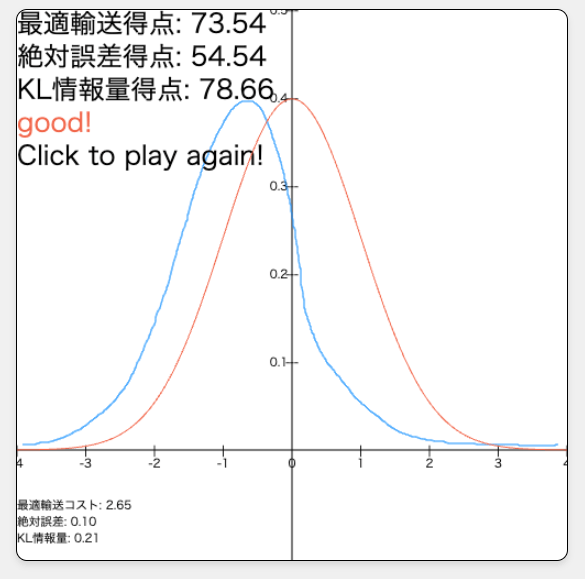
GitHub Pagesを用いたフリーハンド採点サイトのスクリーンショットです。真の分布と比較して、手書きの確率密度関数の"精度"を定量化します。

現在、"ランダム出題モード"ボタンをクリックすると、標準正規分布の他に以下の確率密度関数がそれぞれパラメータや自由度がランダムに変わりながら登場するモードも実装しています。是非、種々の確率密度関数をフリーハンドで描けるか、遊んでみてください。

• 正規分布
• 一様分布
• 指数分布
• ガンマ分布
• T分布
• コーシー分布
• ラプラス分布

なお、私が91.14もの高得点を叩き出せたのは、この採点機能を実装している際に何度もテストで描いて上達したからです^[4]。

フリーハンド確率密度関数のスコア化

ここからは蛇足技術的内容であり、本題です。理想的な確率分布と、フリーハンドで描いたヒストグラムの相違度をスコア化したいのですが、実装には３つのアイデアがありました。

• y軸誤差を用いた評価
• KL-ダイバージェンスを用いた評価
• 最適輸送を用いた評価

まず最初に思いつくのが、素朴に真の分布とフリーハンドとでy軸の誤差を評価する方法です。目立った問題点はなく、ベースライン的に使える方法です。

次に、機械学習などでも度々登場するKL-ダイバージェンスですが、今回は不向きだと思っています。KL-ダイバージェンスは確率分布に対して定義していますが、フリーハンドで描くと通常、積分時の面積（本記事では確率の総和のことを「面積」と表現します。）が1にならず、確率密度関数の定義を満たしません。面積が1になるように正規化すれば良いのですが、それでは描いた時とスケール感が変わってしまうため、基本的には不向きです。

最適輸送も機械学習などでよく登場する技術で、これを用いた評価も考えられます。今回は技術的な面白さや直感的なわかりやすさに加え、不均衡最適輸送によってフリーハンドで描く確率分布の面積が1ではない状況下でも適用できることに着目して採用しました。

以下の節で各評価方法について簡単に解説します。なお、問題設定として、真の確率分布を$p(x)$、フリーハンドで描かれた確率分布を$q(x)$とします。真の分布の定義域はあらかじめ絞って決めておき、その区間のみ評価します。$p(x), q(x)$という表記をすると連続分布っぽく見えますが、離散的にサンプリングし、データ点数$n$の離散値として評価します。

フリーハンドで分布を描くと、通常面積が1にならないので確率分布と呼ぶのは不適切ですが、便宜のためフリーハンド確率分布といった表現を用います。

y軸誤差を用いた評価

y軸誤差を用いた評価とは、各xにおける密度値の絶対差や二乗誤差で評価する素朴な方法です。例えば、以下のような値を評価に用いるアイデアです。

$$\frac{1}{n} \sum_x |p(x) - q(x)| \\ \frac{1}{n} \sum_x (p(x) - q(x))^2$$

フリーハンド分布評価への適用

実装自体が非常にシンプルであり、かつ、フリーハンドと真の分布との差を見る目的においては十分であり、直感的な評価方法ではないでしょうか。他は特に書くことがないので、さらっと流します。

KL-ダイバージェンスを用いた評価

Kullback–Leibler divergence（カルバック・ライブラー情報量とも）とは、2つの確率分布$p(x), q(x)$の差異を計る尺度で、以下のように定義されます^[5]。

$$D_{KL}(p(x) \| q(x)) = \sum_x p(x) \log \left(\frac{p(x)}{q(x)}\right)$$

KL-ダイバージェンスは分布の比較方法として最も有名な方法の1つですが、一般的に問題点もいくつか挙げられます。

1. 距離の公理を満たさない
2. サポートが存在しないとKLダイバージェンスは無限大になる
3. 要素の距離を考慮できない

この辺りの話は有名で、以下の資料には、序盤に最適輸送と比較しながら説明されていますので、ここでの詳細な説明は割愛します。

https://speakerdeck.com/joisino/zui-shi-shu-song-ru-men?slide=7

以下では、これらの問題点が、今回のフリーハンド評価時にはどのような影響があるのかを議論します。

距離の公理を満たさない

2つの分布間の相違度を測りたいだけなので、距離の公理を満たさないことは今回に限っては大きな問題になりません^[6]。

サポートが存在しないと無限大になる

これは真の確率分布の定義域を絞り、その区間に必ずフリーハンドを描画させる制約を課すことで対処可能です。

要素の距離を考慮できない

要素の距離が捉えられないことはフリーハンド評価では不適切に働きうる性質です。例えば以下の図をご覧ください。以下の例では、左右の赤ヒストグラムと青ヒストグラムのKL-ダイバージェンスが一致します。このように（KL-ダイバージェンスの定義式を見ても明らかですが）、分布の比較では要素の距離を考慮できません。

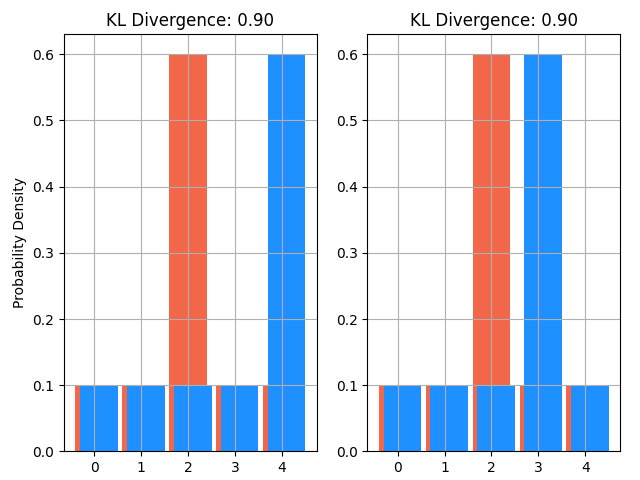
KL-ダイバージェンスが一致してしまう例。直感的には右図の方が分布が近いので、右図の方が相違度が小さくなって欲しい。

この性質はy軸誤差を用いた評価も同様です。

フリーハンド分布評価への適用

KL-ダイバージェンスをフリーハンド評価に用いるにあたって、最も厄介なことは、フリーハンド確率分布は面積が1になる保証はないことです。そのままKL-ダイバージェンスの定義通りに計算させることは可能ですが、今回はフリーハンド確率分布の方を、面積が1になるように正規化してから計算するようにします。この前処理のせいで、直感に合わない点数が出力される恐れがあります。

最適輸送を用いた評価

最適輸送とは

最適輸送とは、2つの確率分布の相違度を計算する方法の1つです。「輸送」という言葉に引っ張られすぎない方がよいのですが、確率分布から一旦離れて、次のような問題設定を考えます。

$n$個の倉庫と、$m$個の工場があります。倉庫$i$には荷物が$a_i$個あり、工場$j$では荷物が$b_j$個必要です。倉庫$i$から工場$j$に1つ荷物を輸送するのにコストが$C_{i,j}$かかるとき、要件を満たす輸送を行うのに必要な最小のコストは？

この説明はこちらのスライドを参照しております。問題設定を式で書くと以下の通りです。

• 入力
  • ベクトル $a \in \mathbb{R}^n, b \in \mathbb{R}^m$
  • コスト行列 $C \in \mathbb{R}^{n \times m}$
• 出力
  • 輸送行列$P\in \mathbb{R}^{n \times m}$

ただし、$P_{i,j}$は、$i$から$j$に輸送する量を表します。倉庫$i$から工場$j$に、荷物を$P_{ij}$個輸送すれば良いということになります。これは線形計画によって以下のように定式化できます。

$$\begin{align*} \text{minimize}_{P \in \mathbb{R}^{n \times m}} & \sum_{i=1}^n \sum_{j=1}^m C_{ij}P_{ij} \\ s.t. \quad & P_{ij} \geq 0 \quad \forall{i,j} \\ & \sum_{j=1}^m p_{ij} = a_i \quad \forall{i} \\ & \sum_{i=1}^n p_{ij} = b_j \quad \forall{j} \\ \end{align*}$$

式の意味を解釈します。まず目的関数$\text{minimize}_{P \in \mathbb{R}^{n \times m}} \sum_{i=1}^n \sum_{j=1}^m C_{ij}P_{ij}$ですが、倉庫$i$から工場$j$に荷物を1つ送ると$C_{ij}$のコストがかかり、それを$P_{ij}$個送ろうとしているので、倉庫$i$から工場$j$への輸送コストは$C_{ij}P_{ij}$です。これを$i,j$の全ての組み合わせにおいて総和をとっています。この総和こそが今回最小化したい総輸送コストなので、$P$を動かすことで総輸送コストを$\text{minimize}$します（$C$はgivenな定数です）。

次に制約条件です。

• $P_{ij} \geq 0 \quad \forall{i,j}$

各$i$から$j$への輸送量は0以上と言っています。負の個数は輸送できないので、必要な制約条件です。

• $\sum_{j=1}^m p_{ij} = a_i \quad \forall{i}$

これは$i$からの輸送量の合計が$a_i$と一致すると言っています。当然、$i$には$a_i$個の荷物があるので、一致しなければなりません。

• $\sum_{i=1}^n p_{ij} = b_j \quad \forall{j}$

これは$j$への輸送量の合計が$b_j$と一致すると言っていますが、この式は先の等式の受け取る側バージョンです。

これらの制約条件によって、輸送量は非負であり、輸送量に過不足がない状態を実現できます。このように、最適輸送は線形計画問題であるため、既存の線形計画ソルバーによって解くことができます。

確率密度関数の比較

先の項の説明では、最適輸送を倉庫$i$から工場$j$への荷物の輸送としていましたが、確率密度（もっと言えばヒストグラム）の相違度の算出に使えます。これは単純な話で、$a \in \mathbb{R}^n$と$b \in \mathbb{R}^n$の2つのヒストグラムがあるとします（$b \in \mathbb{R}^n$というふうに、サイズを両方$n$に変更していることに注意）。このとき、2つのヒストグラムが一致するようにデータを$a$から$b$に「輸送」することを考えます。このときの最適輸送コストこそが、２つのヒストグラムの相違度と考えることができます。注意点としては、$i$から$i$への輸送（実際は輸送していない）も許しているので、（実際は）1つも輸送しないとしてもこの等式は成立します。以下の動画では、2つのヒストグラムが一致するように輸送している様子を描いています。もちろん、コストを計算するブロックを動かす順序は関係なく、最適な輸送方法は1通りとは限りません^[7]。

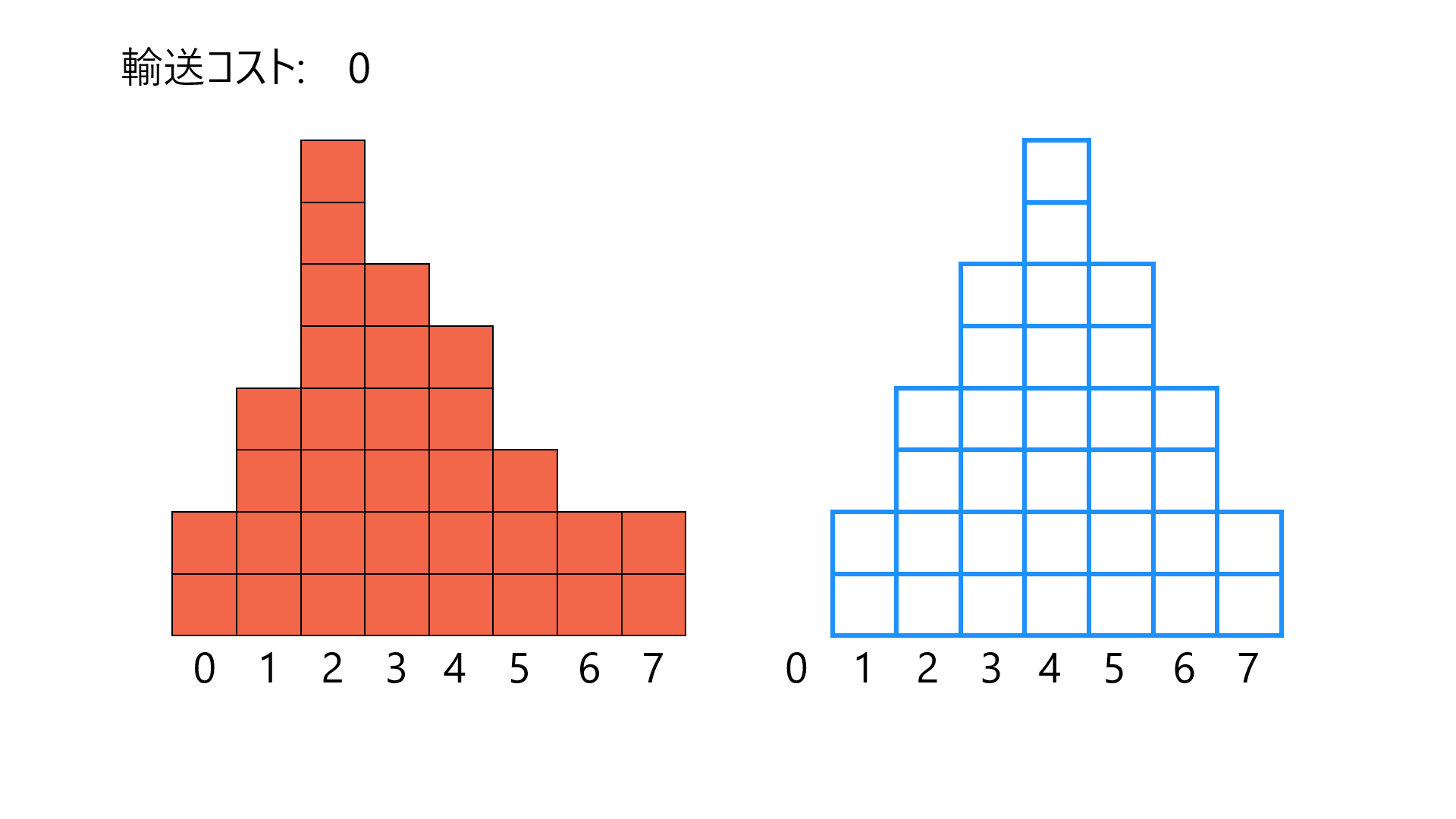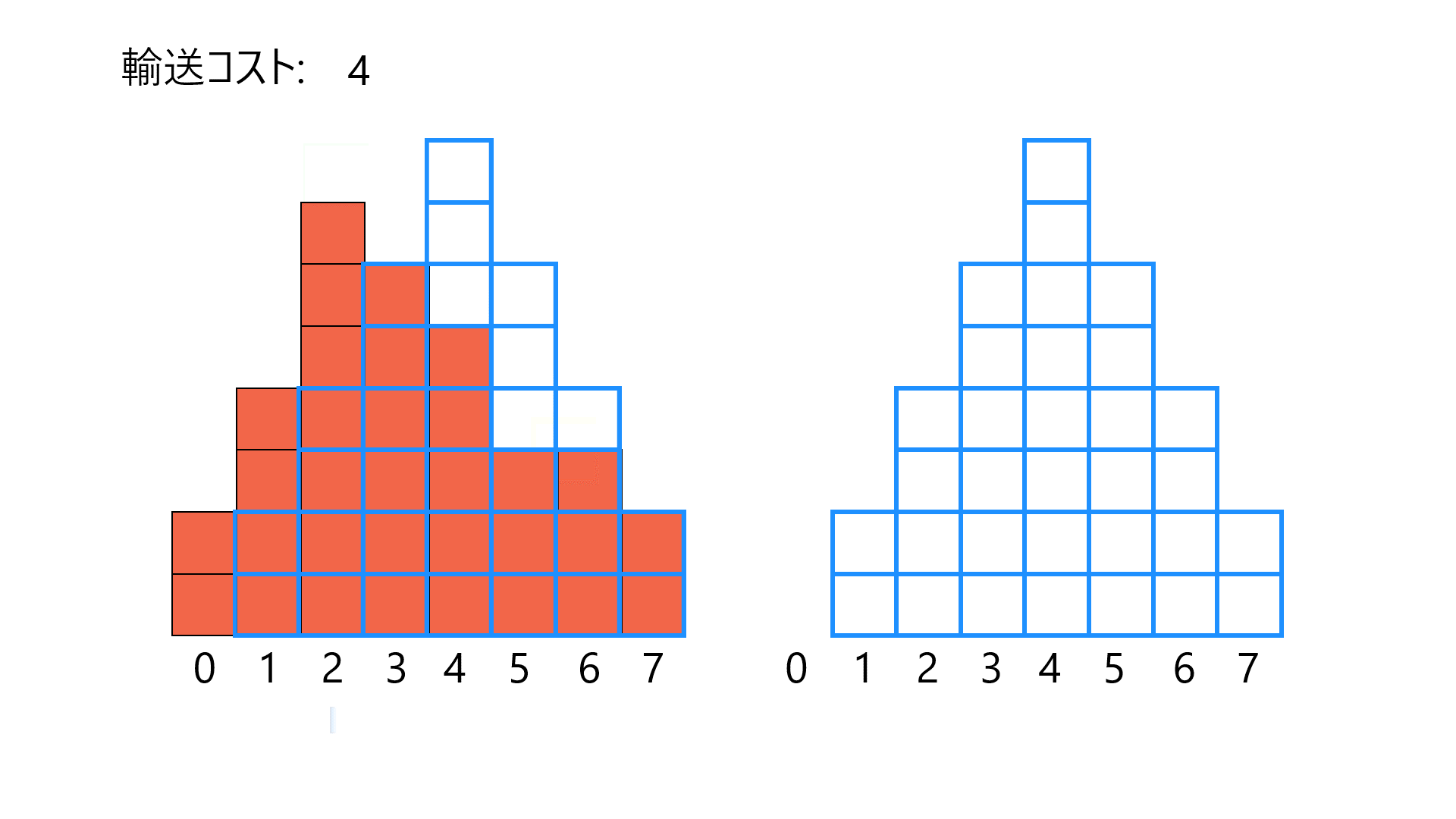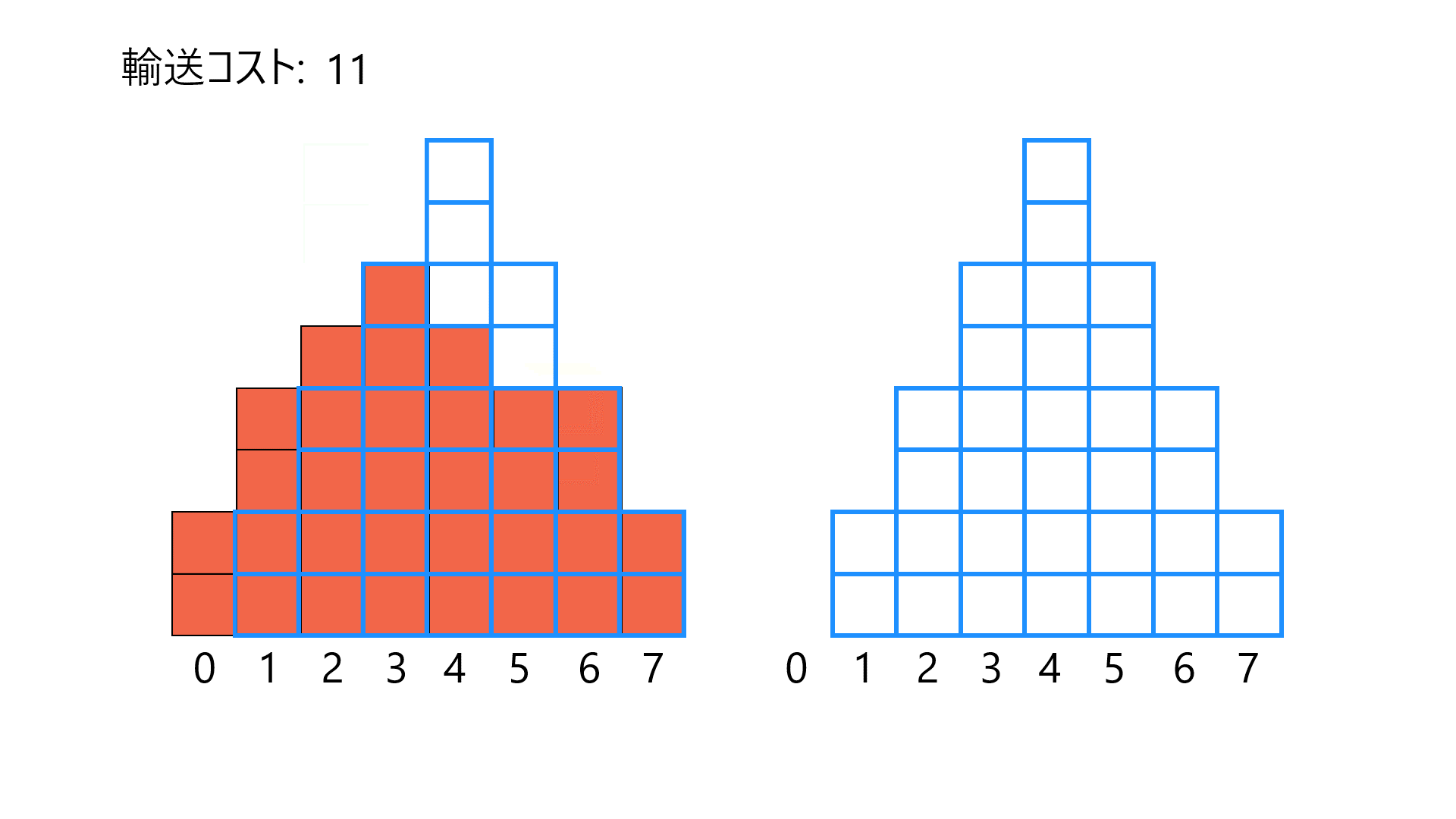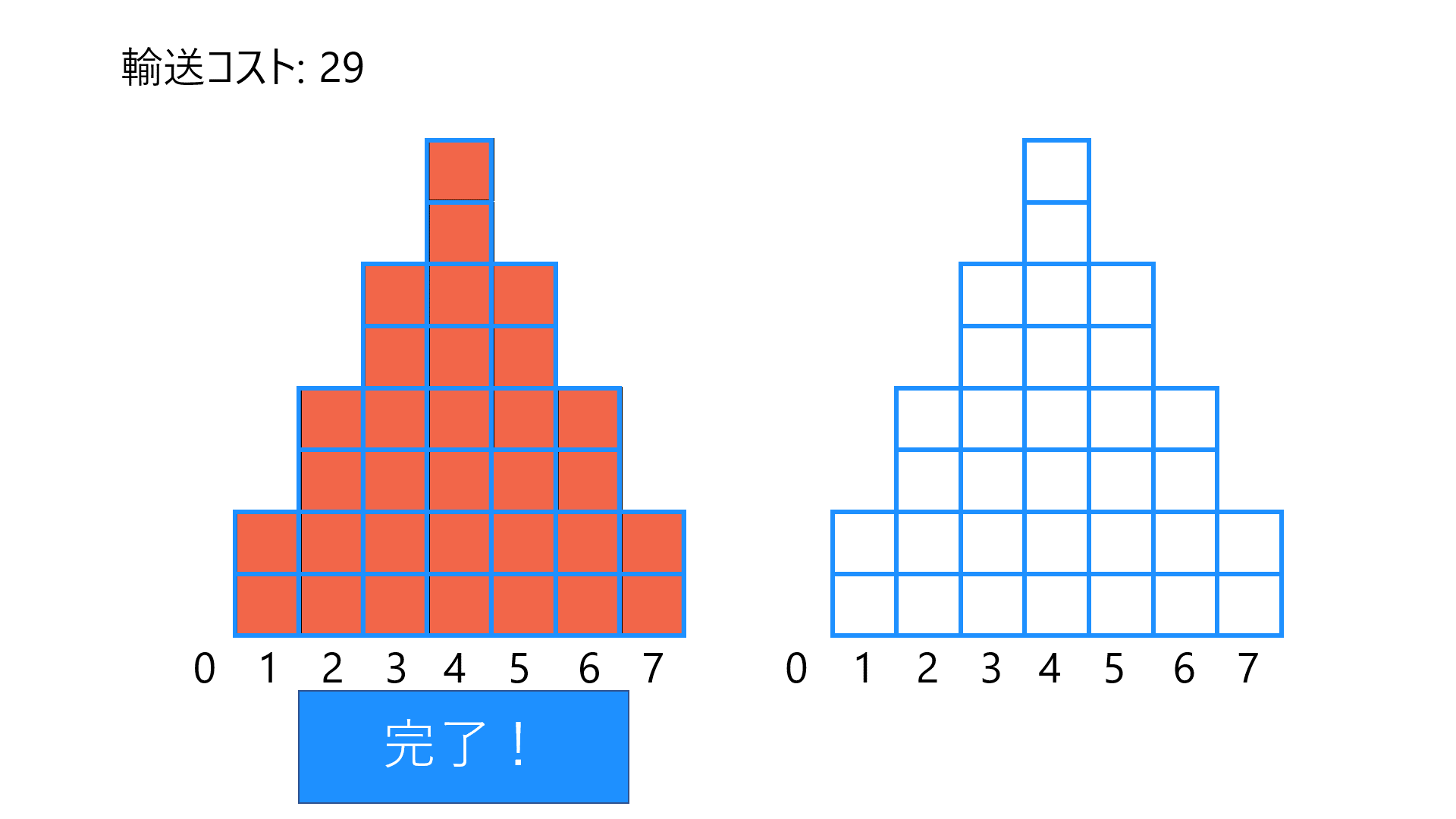
2つのヒストグラム間の輸送コストを計算する例です。左のヒストグラム（赤塗りつぶし）を右のヒストグラム（青枠線のみ）と一致させるように必要な（最小の）輸送コストの和です。簡単のため、1ブロックの質量を1として、距離がそのまま輸送コストとなるようにしています。適切な仮定の元で、この輸送コストをWasserstein距離と呼びます。

フリーハンド分布評価への適用（不均衡最適輸送）

KL-ダイバージェンスでも議論しましたが、フリーハンド分布の方は面積が1になりません。そこで、不均衡最適輸送を用います。不均衡最適輸送では、比較する2つのヒストグラムの総和が一致しない時でも適用できる最適輸送です。先の最適輸送の定式化において、最小化する目的関数にペナルティ項を追加し、制約条件も緩和し、次のように変更します。

$$\begin{align*} \text{minimize}_{P \in \mathbb{R}^{n \times n}} & \sum_{i=1}^n \sum_{j=1}^n C_{ij}P_{ij} + \lambda \|a-\sum_{j=1}^n p_{ij}\|_1 + \lambda \|b-\sum_{i=1}^n p_{ij}\|_1 \\ s.t. \quad & P_{ij} \geq 0 \quad \forall{i,j} \\ \end{align*}$$

ただし、$\|x\|_1$は、$x$の1-ノルム^[8]を表し、$\lambda$は正の定数です。

ここで、最適輸送の対象が確率密度関数同士の比較（面積が両方とも1^[9]）であれば、$\|a\|_1 = \|b\|_1 = 1$が成立しますが、今回は成立しないので、これらの制約を課すことをやめています。そして、目的関数に$\lambda \|a-\sum_{j=1}^n p_{ij}\|_1 + \lambda \|b-\sum_{i=1}^n p_{ij}\|_1$が追加されています。これは、フリーハンドが小さく描かれてしまった場合には足りない分を補填するための生成コストと、フリーハンドが大きく描かれてしまった場合に余分な部分を消し去る削除コストを表しています。

フリーハンド評価の実装上の工夫点は以下の通りです。

• 輸送コスト行列は単純に定義域間の絶対誤差を使う。
• フリーハンドが負の値を描いたとしても、そこに輸送すれば良いので、負の値への特別な処理はしません。
• ヒストグラムのbin数が多いと計算に時間がかかってしまうので、適当にサンプリングしてbin数を調整^[10]する。
• スコアを100点満点にしつつ、それっぽい点数になるよう、スコアは$\text{MAX}(100 -\text{opt-cost} \times 10, 0)$とします（最適輸送コストに10倍したものを100点から減算、0未満は0にする）。

評価方法のまとめ

３つの評価方法のメリット・デメリットを以下にまとめます。

方法	メリット	デメリット
1. 絶対誤差	- 計算が簡単で早い - 直感的に理解しやすい - フリーハンドのy軸値が負であっても扱える	- 要素の距離を考慮できない
2. Kullback–Leibler divergence	- 確率分布の違いを情報理論に基づいて数値化できる - 比較的実装が容易で高速	- 0以下の値を含むビンの扱いに注意が必要 -フリーハンドの面積が1にならない点に対処が必要 - 要素の距離を考慮できない
3. 最適輸送	- 要素の距離を考慮できる - 不均衡最適輸送によって面積が1に近いかどうかを評価観点に含めることができる	- 計算コストが高い - 実装が複雑な場合がある

• 絶対誤差では、縦に対しての誤差だけを見るので、以下のように並行移動しているような図を描くと大幅に点数を失ってしまいます。
• （不均衡）最適輸送では、面積が1にならないペナルティの影響が強いので、多少ずれていても面積が1に近ければそこそこのスコアが出ます。さらに、並行移動であれば輸送コストは小さくなる点も優れています。

各評価方法における相違度（絶対誤差平均、KL-ダイバージェンス、輸送コスト）を100点満点の点数に直す時の匙加減の影響が大きいことがミスリードを生むかもしれません。得点はあくまで「お遊び」であり、参考程度に留めてください。

結び

技術で遊ぶことはとても楽しいです。本記事においては、最適輸送の実装は思いの外楽しかったです（車輪の再発明ですが）。線形計画を解くシンプレックス法^[11]を JavaScript でフルスクラッチしたのは学生時代の課題を楽しんでいるような感覚でした。

実際、今回のようなフリーハンドのスコア化だけが目的であれば、わざわざ不均衡最適輸送を用いる必要はなく、絶対誤差で十分だったかと思います。実務をする上では、目的・納期・予算などから適切な方法を選ぶことになりますが、「技術で遊ぶ」際には自由に、面白いと思った方向で突き進むことが一番です。これからもどんどん面白いことを考えては記事にしていきますので、楽しみにしていてください。最後にもう一度だけフリーハンドチャレンジのリンクを貼って筆を擱きます。技術で遊びましょう！

是非正規分布チャレンジで遊んでいただいて、結果のスクショを撮り、Xで「#フリーハンドチャレンジ」のハッシュタグをつけて投稿してください！（オフィシャル記録^[12]は「最適輸送得点」とします。）
皆様の描く正規分布を心待ちにしております。

https://atsushi-green.github.io/PDF-compete/

参考文献

• 佐藤竜馬. 最適輸送の理論とアルゴリズム. 講談社, 2023.
• 福島雅夫. 新版 数理計画入門. 朝倉書店, 2013.
• 佐藤竜馬. 最適輸送入門. Speaker Deck. 2024年8月26日閲覧.
• 佐藤竜馬. 最適輸送の解き方. Speaker Deck. 2024年8月26日閲覧.

お知らせ

少しでも弊社にご興味を持っていただけた方は、お気軽にご連絡頂けますと幸いです。まずはカジュアルにお話を、という形でも、副業を検討したいという形でも歓迎しています。

https://hrmos.co/pages/zenkigen/jobs?jobType=FULL
https://speakerdeck.com/zenkigenforrecruit/detailed-version-recruitment-materials-for-data-scientists

脚注

1. 執筆執筆当時

2. 字はともかく図を描くのが下手なのはエンジニアとして致命的かもしれませんが、懸命に生きています。

3. マウスやトラックパッド等で描くのは難しいかもしれませんが、ご容赦ください。モバイル端末にも対応しておりますので、タブレット端末とペンをお持ちの方は是非お試しください。

4. この私の正規分布フリーハンド力上達だけでも、このサービスを作った甲斐があったというものです。

5. 評価の際は離散点を用いることになるので、離散表記にしています。

6. 距離の公理を満たさないことは引っかかる気持ちがありますが、フリーハンドの上手さを見るという観点では問題にはならないだろうという意味です。

7. 最適輸送のパターンが複数あっても、いずれか1つでも見つかれば事足ります。

8. $n$次元ベクトル$n$の1-ノルムは、$\|x\|_1 = |x_1| + |x_2| + \cdots + |x_n|$

9. もちろん確率密度に限らず、総和が同じであれば良いです。

10. 1次元では貪欲法で実装すれば高速化できたのですが、つい線形計画で実装してしまいました。

11. シンプレックス法自体が最適輸送、特に一次元の分布間の比較に対して良い方法ではありません。詳しくは参考文献をご覧ください。

12. スコア記録機能やランキング機能もないのにオフィシャル記録とはなんだ？という感じかもしれませんが、ご愛嬌ということでお願いします。