✏️

統計検定®︎準１級は実務で役に立つのか？

redtea

2024/05/27に公開

はじめに

こんにちは。ZENKIGENデータサイエンスチーム所属の廣田です。原籍はオムロンソーシアルソリューションズ株式会社技術創造センタですが、社外出向でZENKIGENに所属しており、数理最適化や機械学習を用いたデータの分析業務、それらの結果に基づいた顧客への提案をしております^[1]。

出向先であるZENKIGENの同僚にも、原籍のオムロンの同僚にも、統計検定®の準1級や1級を持っている方がいて、私も負けじと準1級を受験しました。結果、統計検定®準1級に合格し、優秀成績賞までいただくことができました。

Certificate
統計検定®合格証と優秀成績賞

試験対策を通じて、改めて統計学の考え方は有用と感じました。この手の検定試験は物事を体系的に学ぶきっかけになるため、私個人としては有用な勉強方法と捉えていますが、そこで得た知識が如何に業務でも役に立つかを^[2]本記事でお伝えします。

まだ統計について詳しくない方には、その魅力を感じていただけるように
統計検定®を受験しようか迷っている方/受験しようと思っているがなかなか手につかない方にとっては、勉強のモチベーション向上の一助に
既に統計検定®を取得されている方には「うんうん」と頷いて楽しみながら読んでいただけるように

と思いながら本記事を執筆しました。

なお、統計検定®の勉強方法や受験エピソードについては他にたくさん記事が出ていますので、本記事では言及しません。

統計検定®とは

統計に関する知識や活用力を評価する全国統一試験です。

詳しくは公式HPをご覧ください。
https://www.toukei-kentei.jp/about/

準1級

準1級は今回私が受験した試験区分です。

統計学の活用力 ─ 実社会の課題に対する適切な手法の活用力

が問われます。統計検定®の中でも、最も実践的な試験区分かもしれません。

統計検定®準1級の特徴は、試験範囲の広さです。是非一度以下のリンクからその試験範囲をご覧ください。学ばねばならぬ項目が多いですよね。

これらたくさんある各項目が実社会で生かされているのは興味深くありませんか？ 1つの記事で多くを取り上げることはできませんが、私が面白いと感じたトピックを2つ抜粋して紹介させていただきます。

統計学が役立つ事例紹介

この章から本題です。

統計検定®準1級の広範な試験範囲を見ていると、回帰分析、多変量解析、時系列解析などは応用的手法であり、実際の分析で用いられることが想像できると思います。一方で、「統計的推測の不偏性や一致性」といった基礎的な概念ほどその価値に気づきにくいと思います^[3]。今回はこの性質を知っていることの有用性を是非お伝えしたいです。

また、「欠損を含むデータの扱い」については最近統計検定®を通じて学んだ知識を直接業務で役立てられたので、これも紹介します。

推定量の不偏性・一致性

まずは推定量についてお話しいたします。いきなりですが1題出題します。

問題

辺の長さが $\mu$ の正方形の鋳型から作られた、およそ同じ大きさの正方形がたくさん^[4]あり、この鋳型の面積 $S$ が知りたいとします。残念なことに、鋳型は壊れてしまったので、鋳型の辺の長さは測定できません。そこで、たくさんある正方形から、 $n$ 個の正方形を適当^[5]に選んで、各正方形の辺の長さを計測、記録しました。このようにして得られたデータを $x_1, x_2, \ldots x_{n}$ とします。あなたならどのように計算して、正方形鋳型の面積 $S$ を推定しますか？その時の推定量を $\hat{S}$ とします。ただし、各辺の長さ $X$ は $X_i \sim N(\mu, \sigma^2)$ とします( $\mu, \sigma$ は未知)^[6]。鋳型の面積 $S$ は、鋳型の辺の長さ $\mu$ を用いて、 $S=\mu^2$ とします^[7]。

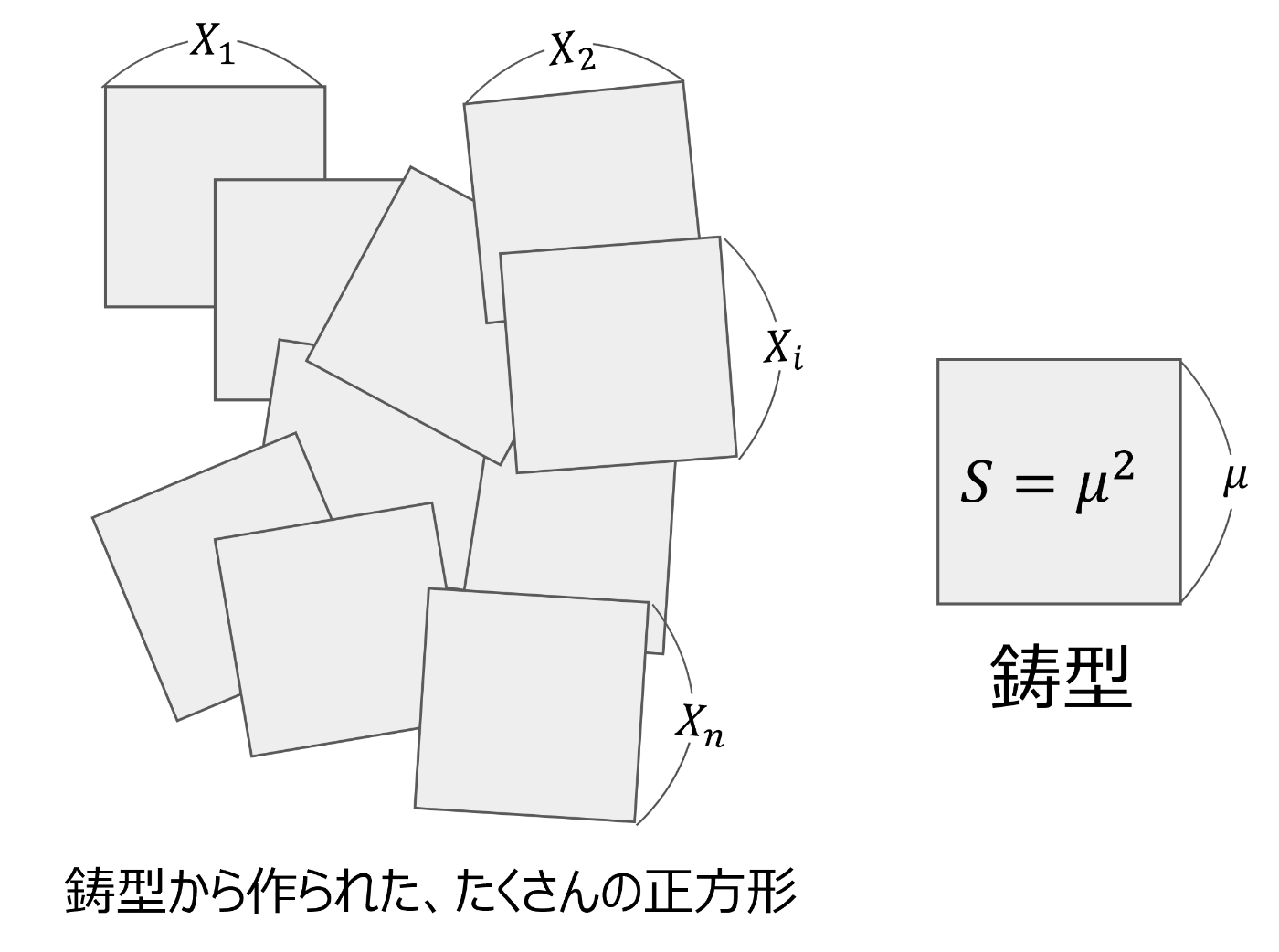
square
たくさんある正方形の辺のデータ $X$ を集めて、面積 $S$ を推定する。

問題に対する議論

多くの方は以下の1または2の方法を思いついたのではないでしょうか。
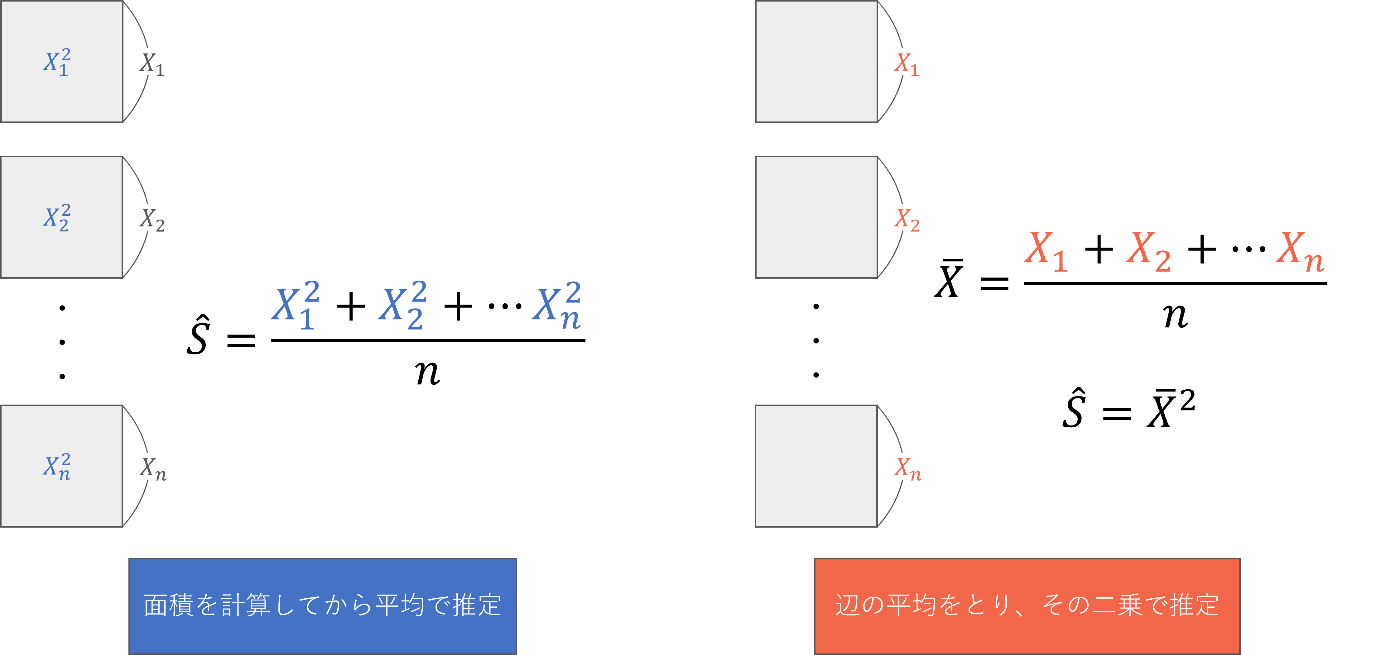
solve1
推定方法の例。1. それぞれの正方形の面積を計算してから平均をとるか、2. 辺の平均を二乗して面積を求める、というのがパッと思いつく推定方法。

その他にも、

n個からさらに1つ適当に選んで、その面積を計算する。
大きい順に並べて、 $n/2$ 番目か $(n+1)/2$ 番目の正方形の面積を選ぶ。
大きい順に並べて、1位と $n$ 位を除いて、そこから平均を取るなりなんなりする方法。

など、これだけ単純な問題設定であっても様々な方法が考えられます。この時、不偏性や一致性を知っていると、どの方法が最も適しているかを判断できます。では一度堅苦しい不偏性と一致性の定義を確認します。しばしご辛抱ください。

不偏性

推定量の不偏性とは、書いて字のごとく、推定量が偏っていない性質のことです。ある本当の値^[8] $\theta$ を推定したいときに、 $\hat{\theta}$ という値で推定したとき、 $\theta$ が不偏推定量であるとは、式で書くと以下の通りです。

E[\hat{\theta}] = \theta

式を解釈すると、推定を何度もやれば真の値周辺に分布するという感じでしょうか。必ずしも $\hat{\theta}$ が $\theta$ にならなくてもよく、平均が $\theta$ になれば良いというのがポイントです。

今回の正方形の面積を推定する例で置き換えると、一辺の母数は $\mu$ としているので、

E[\hat{S}] = \mu^2

であれば不偏性を満たすことになります。もしこれを満たさない推定量を用いてしまうと、本当に得たい $\mu^2$ とはズレた(偏った)値になってしまって、望ましくありませんね。

一致性

推定量の一致性とは、こちらも文字通り、その推定量が真の値と同じになる(一致する)性質です。不偏性と混同しやすいでですが、不偏性とは似て非なる概念です。 $\hat{\theta}$ が $\theta$ の一致推定量であるとは以下の条件を満たすことです。

\forall{\sigma} > 0, n \rightarrow \infty, P(|\hat{\theta} - \theta|>\sigma) =0

やや複雑な式ですが、解釈は、「 $n$ (=データ数)が多くなれば、推定量は真の値に近づいていく」です。これも重要な性質で、日本の成人男性の平均身長を求めるのに、計測する成人男性が増えれば増えるほど信憑性の高い結果が得られるような直感を表します。

各推定量の性質の確認

さて、問題に戻ります。まず、1.の方法について考えてみます。各正方形の面積は ${x_i}^2$ なので、面積の平均値は $\frac{1}{n} \sum_{i=1}^{n} {x_i}^2$ です。これの期待値を計算した結果は次式の通りです^[9]。

E[\frac{1}{n} \sum_{i=1}^{n} {x_i}^2] = \frac{1}{n} n E[{X_i}^2] = E[X_i]^2 + V[X] = \mu^2 + \sigma^2

なお、計算の途中で分散公式というものを使っています。こちらの解説が詳しいのでおすすめです。次に、2.の方法について考えてみます。こちらも分散公式と、 $V[\bar{X}] = \sigma^2/n$ であること^[10]を利用すると、次の計算結果が得られます。ただし、 $\bar{X}$ は標本平均(= $n$ 個の正方形の辺の平均値)を表します。

E[\bar{X}^2] = E[\bar{X}]^2 + V[\bar{X}] = \mu^2 + \frac{1}{n}\sigma^2

なんと、1.の方法では $n \rightarrow \infty$ としても、 $E[\hat{S}] = \mu^2 + \sigma^2$ のままなので、不偏性も一致性もありません。

ならば2.はどうでしょうか。確かに $n \rightarrow \infty$ とすれば $E[\hat{S}] = \mu^2$ なので一致性はありますが、不偏性はありませんね。 $\sigma^2/n$ の分だけ大きめに $S$ を推定してしまいます。すなわち、計測データ件数^[11]が少ないと、2.の方法であったとしても正しい値を推定できませんし、1.の方法に至ってはどれだけ多くのデータを計測したとしても、正しい面積を推定できないのです^[12]。

解答例

では、どのようにすれば妥当に面積の推定量の期待値が $\mu^2$ になるように推定できるのでしょうか。やり方は意外とシンプルな(ただし、問題設定の単純さからすると複雑な計算を要する)方法で推定できます。アイデアは、大きめに推定してしまう $\sigma^2 /n$ の分だけ引き算で相殺することです。

不偏分散の推定値 $\hat{U^2}$ を

\hat{U^2} = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2

とします。この $\hat{U^2}$ には、

E[\hat{U^2}] = \sigma^2

という性質があります。この $\hat{U^2}$ を用いて、

\hat{S} = \bar{X}^2 - \hat{U^2}/n

で推定すれば、

E[\hat{S}] = E[\bar{X}^2 - \hat{U}^2/n] = E[\bar{X}^2] - E[\hat{U}^2]/n = \mu^2 + \frac{1}{n}\sigma^2 - \frac{1}{n}\sigma^2 = \mu^2

が得られ、不偏性と一致性を満たす推定量を得ることができます。このことから、「辺の長さの平均を求めて二乗したものから、不偏分散をnで割ったものを引く」が正解^[13]^[14]です。

以上のように、各辺の長さのデータが得られているときに、単に面積を求めるシンプルな問題設定ですら不偏性や一致性がない推定量を計算してしまう恐れがあります。この罠に気づくためにも、体系的に統計を学ぶ価値があるのではないでしょうか？

簡単に実験

式だけでは理解できても腹落ちしない方もいらっしゃるかと思い、Pythonを用いて簡単にシミュレーションしてみました。シミュレーション設定は以下の表の通りです。なお、ソースコードは以下のGitHubに公開しておりますので、是非母数やサンプルサイズを変えてお手元でもお試しください。お手元で設定を変えて実行すると、グラフの形が大きく変わることがあります。その理由は本題から外れるので、注釈にて説明します $\rightarrow$ ^[15]。

パラメータ	値
正方形の1辺の長さの平均母数 $\mu$	5
正方形の1辺の長さの標準偏差母数 $\sigma$	1
正方形の面積母数 $S = \mu^2$	25
サンプルサイズ $n$	5
試行回数	10000

まずは各正方形の面積を求めてから平均をとる方法1.です。この推定方法では不偏性も一致性もなく、面積の平均値が25.99で、約1.0過大評価してしまっています。これはまさに、 $\mu^2 + \sigma^2 = 5^2 + 1^2 \fallingdotseq 25.99$ を表しています。理論通りですね。

area
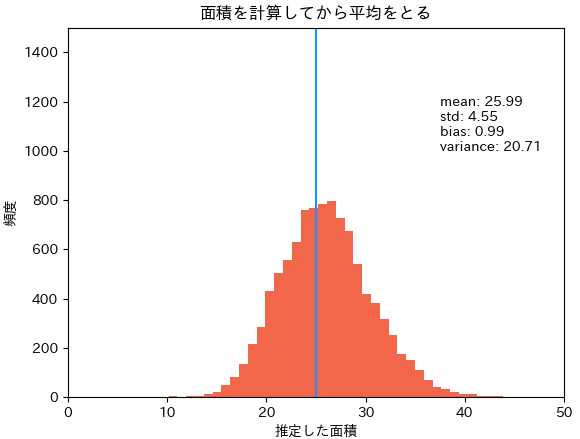
方法1: 各正方形の面積を求めてから平均をとる。

次に先に辺の平均を求め、二乗する方法2.です。この方法は一致性があるので、サンプルサイズ $n$ を無限大にすることで $\mu^2=25$ と正しく推定できますが、今回はサンプルサイズを $n=5$ とあえて小さめにしています。その結果、 $\sigma^2 + \sigma^2/n = 5^2 + 1/5 \fallingdotseq 25 + 0.19$ という、0.19だけバイアスが生じた結果を得られています。理論通りは気持ちいい！

side
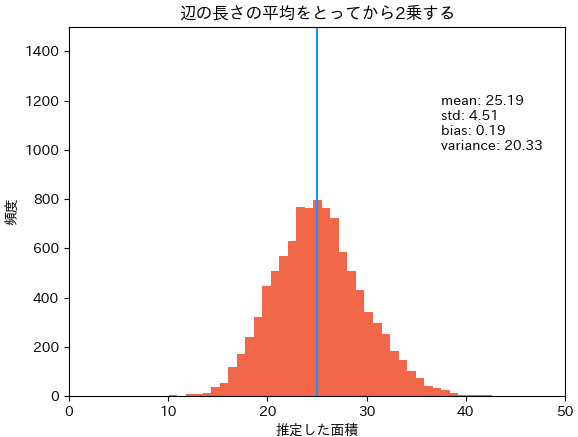
方法2: 辺の平均を求め、二乗することで面積を推定する。

最後に、方法2.の結果がらバイアス(偏り)を取り除く方法3.です。方法2の $\sigma^2/n$ を不偏分散の推定値 $\hat{U}$ を $n$ で割ったもので引きます。結果、 $\mu^2=24.99$ という限りなく母数に近い値を導き出すことができました。

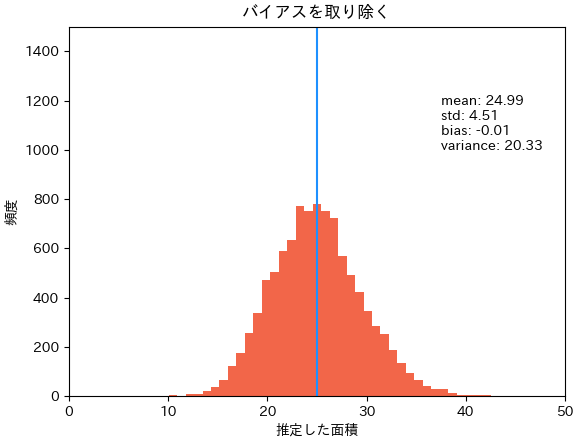
unbiased
方法3: 辺の平均を求め、二乗する方法2から、不偏分散の推定値を $n$ で割ったもので引くいてバイアスを補正する。

上記3つのヒストグラムを見ると、概ね分布の山が25付近にあるように見えるので(定性的に)大きな問題はないように見えるかもしれませんが、定量的にはしっかり偏りを含んだ結果になってしまいます。この小さなズレが大きな問題を生んだり、問題設定によっては小さなズレでは済まないこともあるでしょう。

欠損を含むデータの扱い

欠損データとは

実務でデータ分析をやっていると、必ずといっていいほど欠損データと出会します。 $p$ 次元の $n$ 個体分のデータを全て得られた時に全データとしたとき、 $n \times p$ 個の数字(スカラー値)が得られている状況を考えます。ここでの欠損とは、 $n \times p$ 個の数字うち、いくつかの数字を知ることができないことを欠損と言います。例えば、 $n$ 人の学生が英語の中間試験と期末試験を受験する際( $p=2$ )、いずれか^[16]の試験を欠席した人がいると、欠損データが生じます。

欠損データは、その欠損のメカニズムから以下の3種類に分類されます。

MCAR(Missing Completely At Random): 欠損は、欠損データおよび観測データの両方ともに依存せず、完全にランダムに生じる。
例えば、ランダムに風邪を引いた学生が試験を受けなかった場合。
MAR(Missing At Random): 欠損は、観測データに依存して生じるが、欠損データの値に寄らない。
例えば、中間試験(観測データ)が高得点だった人には期末試験を免除した場合。
MNAR(Missing Not At Random): 欠損は、欠損データそのものの値に依存する。
例えば、期末試験の点数(欠損データ)が低かった学生の答案を見た先生が、ブチギレて答案用紙を破り捨ててしまった場合^[17]。

欠損データの扱い方

欠損データに対する扱い方はいろいろありますが、大きく分けて、

欠損値を何らかの方法で埋めて全データが揃っていることにして分析を進める^[18]
削除法^[19]: 欠損を含む個体データは諦めて、 $p$ 次元のデータが揃っている個体だけで分析を進める

のどちらかです。欠損を埋めて使う場合では、どのように埋めるかというのも重要です。簡単に思いつく方法として挙げられるのは、

平均補完: その項目の平均値で埋める(中間試験を受けなかった人のデータを、中間試験の平均点で埋める)
回帰補完: (回帰分析などで)、予測して埋める(中間試験を受けなかった人のデータを、期末試験のデータから予測して埋める)

などがあるでしょう。しかし、分析の目的によっては平均で埋めたり、回帰予測結果で埋めるのは適切でない場合が多いです。これらの欠損処理方法がどのような悪影響を及ぼすのか、次節で見ていきます。

欠損処理による悪影響

目的に応じた欠損処理を行わないと、どのような悪影響が考えられるか、シミュレーションしながら確認していきます。シミュレーション設定は先の例と同様、次の通りとします。

2変量正規分布を想定し、それぞれXとYのデータがあります。
- 例えば、Xは中間試験の点数、Yは期末試験の点数とします。
- 試験を受ける人数は3000人とします。
- XとYには相関関係があります( $Y = X + N(0, 0.2^2), X\sim U(0,1)$ ^[20]を表します。)。
中間試験は全員受けたとします(Xは全数揃って、3000人が受験)。
以下の要領で、期末試験データには3パターンの欠損が生じることをそれぞれ考えます(Yに欠損)。
- MCARでは、期末試験だけランダムで全体の10％の人が受けられなかったとします。
- MARでは、中間試験の成績上位20％が期末試験を免除されるものとします。
- MNARでは、期末試験の成績下位20％の答案用紙が破り捨てられる^[21]とします。

シミュレーションに用いたソースコードは以下のリポジトリにおいてありますので、手元で動かしたい方は是非ご利用ください。

削除法

削除法(欠損データを補完しない)を用いた時、以下の表のような結果となります。

欠損が完全にランダムに生じる場合(MCAR)は、補完をする必要はなく、そのまま分析することで正しいYの平均、相関係数、傾きを得ることができます^[22]。
Yの平均: Yが大きい値や小さい値について欠損が起こりやすい設定になっているので、補完をしないとYの平均値を過小評価したり、過大評価したりしてしまいます。
Yの標準偏差: MCARの場合は全体的にデータ件数が減るだけなので変わりないですが、MARやMNARでは端のデータが消えてしまうので、データの範囲が狭くなり、標準偏差は小さくなります。
相関係数: MARやMNARの場合は、欠損により端のデータを欠くので、相関係数を過小評価してしまっています。
回帰直線の傾き: MNARの際、偏りを与えてしまいます(他の欠損メカニズムでは偏らない)。これは偶然Xが小さくYが大きいデータは残るのに、偶然Yが小さくXが大きいデータが欠損することに起因します。MARの場合はYに依らずに欠損するので、回帰直線の傾きは偏りなしで推定できます。

欠損メカニズム	Yの平均	Yの標準偏差	相関係数	傾き
MCAR	偏りなし	偏りなし	偏りなし	偏りなし
MAR	過小評価	過小評価	過小評価	偏りなし
MNAR	過大評価	過小評価	過小評価	過小評価

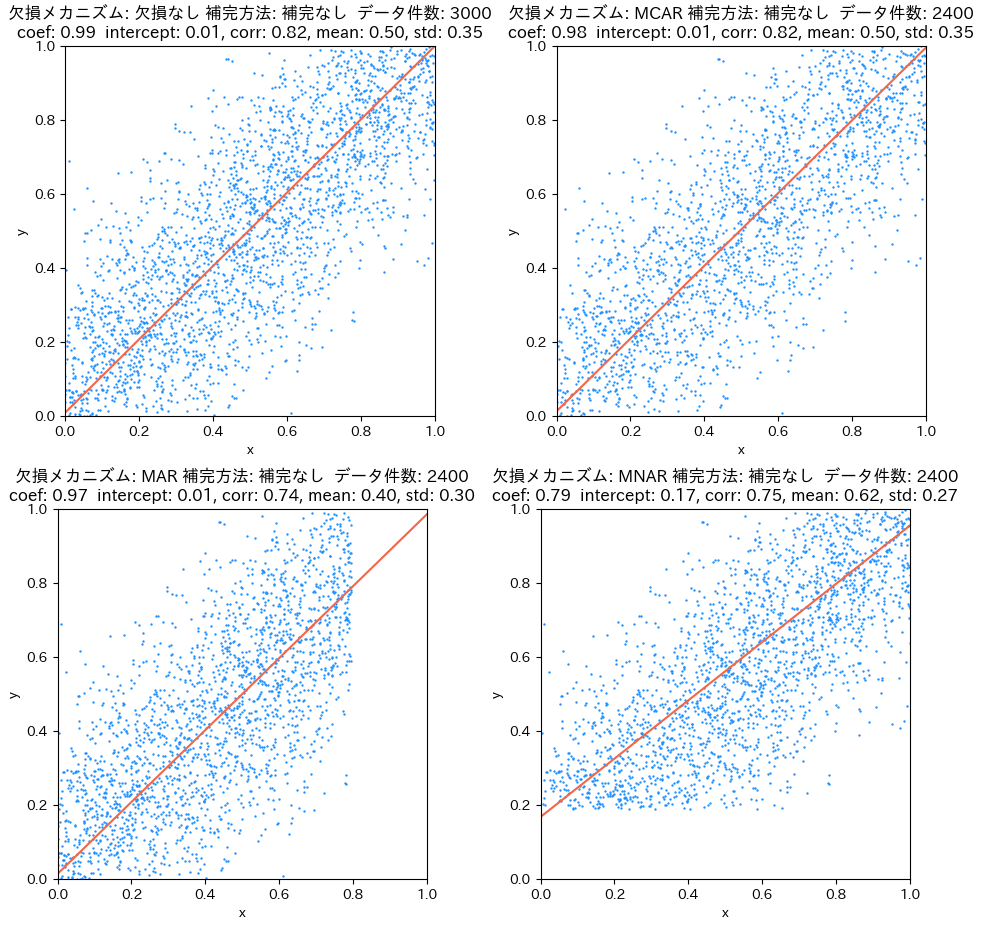
delete_method
補完をしない場合。図左上は欠損が生じていない時の図で、これをベースと捉えてください。図右上がMCAR、左下がMAR、右下がMNARで欠損を生じさせたときの回帰直線と各種統計量です。

平均補完

平均値を用いて欠損補完すると、以下の表のような結果となります。

欠損メカニズム	Yの平均	Yの標準偏差	相関係数	傾き
MCAR	偏りなし	過小評価	過小評価	過小評価
MAR	過小評価	過小評価	過小評価	過小評価
MNAR	過大評価	過小評価	過小評価	過小評価

以下の図の右上をご覧ください。欠損がランダムに生じる場合(MCAR)であっても、全て平均値を埋めてしまうのでY標準偏差が小さくなったり、Yの平均・相関係数・傾きに悪影響が出ていることがわかります。また、左下のMARや右下のMNARの図を見ても、欠損値を平均で埋めるとあらゆる統計量に影響が出てしまいます。

mean
平均で埋める場合。図左上は欠損が生じていない時の図で、これをベースと捉えてください。図右上がMCAR、左下がMAR、右下がMNARで欠損を生じさせたときの回帰直線と各種統計量です。欠損したYをYの平均値で埋めている様子が、青色の横線で見て取れます。

回帰補完

回帰分析で予測した値を用いて欠損補完すると、以下の表のような結果となります。

欠損メカニズム	Yの平均	Yの標準偏差	相関係数	傾き
MCAR	偏りなし	過小評価	過大評価	偏りなし
MAR	偏りなし	過小評価	過大評価	偏りなし
MNAR	過大評価	過小評価	過大評価	過小評価

図と統計量をよく見比べると何が起きているかよくわかります。回帰補完は平均で埋めるのと異なり回帰直線上に(欠損)データをプロットすることになるので、一般的には相関が強くなります。ただ、回帰補完はデータの分布を歪めるので、相関が弱くなる影響もあり、相関の変化はケースバイケースです。Yの平均の変化は、どんな条件で欠損が生じるかで変わります。また、データのばらつきは小さくなる方向に補完するので、標準偏差は小さくなります。

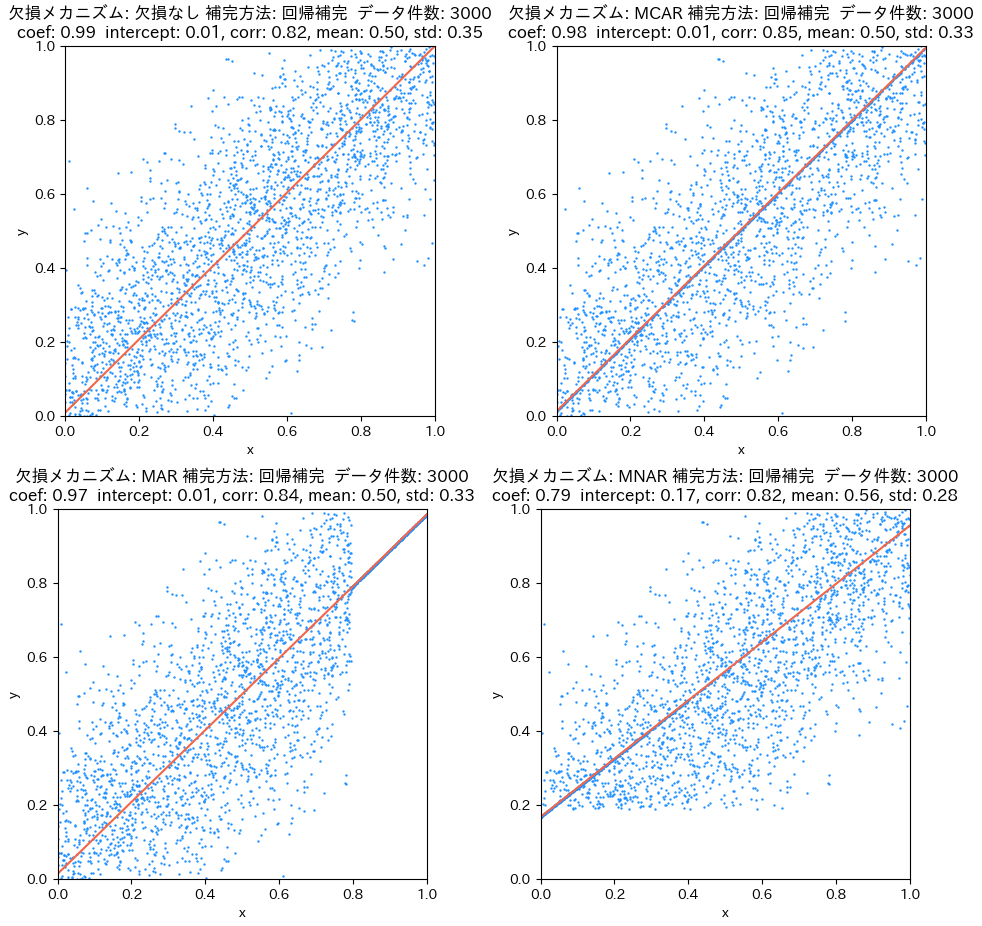
regression
回帰により埋める場合。図左上は欠損が生じていない時の図で、これをベースと捉えてください。図右上がMCAR、左下がMAR、右下がMNARで欠損を生じさせたときの回帰直線と各種統計量です。分かりにくいですが、欠損を線形回帰で補完しているので、欠損補完したデータが赤い回帰直線の上に並んでいます。

欠損データの扱い方まとめ

3種類の欠損メカニズムと、3種類の欠損データへの対処例を可視化してみました。欠損データを埋めることは多くの場合で統計量に偏りを生じさせる原因になります。しかし、欠損を埋めて使わないとデータ件数が足りないということは非常によくあります。その際にはどんな悪影響が出るかを知った上で、目的に応じた補完方法を選択し、分析を進めることが必要です。

ZENKIGEN業務での欠損データ例

私はZENKIGENのサービス、「エントリーファインダー(EF)」のデータ^[23]をはじめとする、採用選考データを分析し、顧客に報告する業務も担当しています。企業の採用プロセスによっては、例えば書類選考通過者にのみ適性検査を受験してもらう、といった運用がなされており、必ずしも応募者全員の全データを得ることはできません。この欠損メカニズムは、書類選考(観測データ)が不合格であった学生の適性検査データ(欠損データ)が得られないので、MARであり、扱いに注意が必要です^[24]。採用データを扱う我々によって、欠損データを扱う手法は非常に重宝します。

結び

先人たちのお陰で、PythonやRのライブラリを用いれば機械学習アルゴリズムや統計処理、データの前処理・可視化までもを容易に行えます。分析方法も検索すれば出てきますが、注意点や観点を体系的な知識として持っていないと、足元をすくわれることになりかねません。実際、本記事で紹介したような不偏性や一致性のない値を推定して顧客に報告する訳にはいきませんし、欠損しているからといって目的にそぐわない方法で埋めたデータで分析するのは以ての外です。このような失敗を犯すリスクを自力で減らすためには、統計の基礎的な知識を体系的に身につける他ないと考えています。

統計について偉そうに書きましたが、私は満点で合格しわけでもないですし、1級を持っているわけでもありません^[25]。より科学的に正しい方法で分析を行えるよう研鑽の日々です。本記事を通じて、少しでも統計って面白いなと思っていただければ幸いです。

参考文献

一般社団法人日本統計学会, 日本統計学会公式認定統計検定準1級対応統計学実践ワークブック, 学術図書出版社, 2020.
久保川達也, 現代数理統計学の基礎, 共立出版株式会社, 2017.

お知らせ

少しでも弊社にご興味を持っていただけた方は、お気軽にご連絡頂けますと幸いです。まずはカジュアルにお話を、という形でも、副業を検討したいという形でも歓迎しています。

脚注

執筆当時 ↩︎
統計検定準1級の過去問を見ると問題自体が業務の例みたいになっているので、統計検定®準1級の受験者は統計検定®が如何に役立つかは既にご存知かもしれません。 ↩︎
これらの基礎の上に応用があるので、大事な考えということは大前提です。 ↩︎
具体的な数値は想像にお任せしますが、100とか1億とか、そのあたりの数値を想像してください。 ↩︎
この「適当に選ぶ」ための方法に、試験範囲の1つの章が割かれています。本記事では述べませんが、適当に選ぶことは意外と難しく、とても重要です。 ↩︎
統計に詳しくない方向けの補足です。辺の長さの「本当の値」が $\mu$ だと信じます。そして、各正方形の辺にはばらつきがあり、さらに計測すると計測時の誤差も含みます。それらのばらつき度合いを $\sigma$ と考えます。すなわち、 $X$ は平均 $\mu$ , 分散 $\sigma^2$ の正規分布に従うものとします。実は正規分布の仮定をおかなくともこの問題は成立しますが、簡単のために正規分布としています。 ↩︎
Xにて、@st4tditt0 様からのご指摘をいただきました。今回推定したい対象は、 $S = \mu^2$ です。 $\mu$ は母数なので、神のみぞ知る値であり、実際に観測すると $\mu$ から少しズレた値が得られます。この少しズレたデータ $x_1, x_2, \ldots x_{n}$ から、母数 $\mu$ の二乗値をどのように推定するか、という問題設定です。 ↩︎
母数と言われるものです。 ↩︎
統計に慣れ親しんでいないと、「平均値の期待値」という表現に違和感を覚え得るかもしれないので補足します。 $\frac{1}{n} \sum_{i=1}^{n} {x_i}^2$ で得られた面積平均値は、正方形を $n$ 個サンプリングして推定した1回の試行です。そしてその期待値というと、もし仮にこの $n$ 個の正方形をサンプリングして面積を測るという試行を何度も繰り返した際の平均を意味します。 ↩︎
$V[\bar{X}] = V[(X_1 + X_2 + \cdots + X_n)/n] = V[(X_1 + X_2 + \cdots + X_n)]/n^2$ となり、 $X_1, X_2, \cdots, X_n$ は独立であるから、 $nV[X_i]/n^2 = \sigma^2/n$ を導けます。 ↩︎
サンプルサイズ ↩︎
私が初めてこの計算をしたときはとても感激しました。この感激を伝えたくこの記事を書いたといっても過言ではありません。 ↩︎
実際はデータ特性や目的に応じて変わりますが、特殊な状況は考えない場合の話です。 ↩︎
これはあくまでも一つの解答例です。他にもリサンプリング手法の一つであるジャックナイフ推定量を用いるなどがあります。 ↩︎
掲載したヒストグラムは一見、中心極限定理でかなり正規分布に分布収束しているように見えますが、完全には分布収束しきっていません。元の分布は、面積の推定量の分布は正規分布に従う辺の二乗で与えられるので、非心カイ二乗分布に従います。今回のシミュレーションでは、辺の正規分布の標準偏差を1にしているので、非心カイ二乗分布に従います。平均が0なら自由度1のカイ二乗分布でしたね。 ↩︎
もちろん両方とも欠席した人も欠損データです。 ↩︎
真面目な例を挙げると、センサーの性能都合で一定の値より大きい/小さい値を観測できない、といったことはよくあります。 ↩︎
このような方法は総じてimputation methodと呼ばれているそうです。 ↩︎
英語ではdelete methodというそうです。 ↩︎
$U(0,1)$ は、0~1までの一様分布 ↩︎
本来は不可を出す答案は問い合わせに対応できるように、特に残しおく必要があるはずなんですが。 ↩︎
データ件数が減ってしまうので、推定精度には注意が必要です。 ↩︎
自己PRする動画を応募者が企業に送り、その動画を解析することで応募者の特性を定量化する機能を有します。 ↩︎
実際のデータは相関関係がはっきりしておらず、1次式では表せない関係を持つことも多く、よく~~楽しませてもらっています~~頭を悩ませているものです。 ↩︎
そして1級を持っているからといって万全というわけでもないですね。 ↩︎

ZENKIGENテックブログPublication

私たちは「はたらく人の理想」をつくるために、ITと科学で組織課題に立ち向かうAIテックカンパニーです。「テクノロジーを通じて人と企業が全機現できる社会の創出に貢献する」のVisionのもと、人の感覚に寄り添うテクノロジーを用いたでサービスを展開しています。

Discussion

yan0022

素晴らしいノートありがとうございます。図や表がとても丁寧で、見ていて気持ちよかったです(マジで)。
ちょっと気になったのが、欠損値の処理についてです。正規分布していないの場合、平均値よりもmedian/most_frequentを使う方がいいじゃないかなと考えています(sklearn SimpleImputerのパラメータとして使えます)。
また、KNNImputerも良さそうものです。「imputation method」に近いですが、KNNを用いて近接する値を探し、それらの平均値や距離を重み付けして補完するというアプローチも直感に合うと思います。

from sklearn.impute import SimpleImputer, KNNImputer

simple_imputer = SimpleImputer(strategy = "median") #{"mean", "median", "most_frequent", "constant"}
data_si = simple_imputer.fit_transform(data)

knn_imputer = KNNImputer(n_neighbours = 5, weights = "distance") #{"uniform", "distance"}
data_knni = knn_imputer.fit_transform(data)

redtea

コメントありがとうございます！
このようなコメントをいただけますと大変励みになります。

特に正規分布していないデータに対しては、おっしゃる通り、中央値/最頻値/近傍平均値などを用いるのは直感的に良いですね。
サンプルコードまで、ご丁寧に書いてくださってありがとうございます。

欠損値補完はケースバイケースで難しいですが、（本記事では触れておりませんが）多重代入法も忘れてはならないアプローチの一つですね。